水平成层场地地震反应的集中质量切比雪夫谱元分析方法*
2022-03-31王竞雄李鸿晶邢浩洁
王竞雄 李鸿晶, 邢浩洁
1) 中国南京 211816 南京工业大学工程力学研究所
2) 中国北京 100081 中国地震局地球物理研究所
引言
覆盖土层对地震波传播特性具有重要影响(高武平等,2012;李平等,2012),通过土层地震反应分析获得工程场地的地面运动特征,为工程结构抗震评估、设计和加固提供依据.许多实际工程场地都可以被简化为水平成层场地模型,即假定覆盖土层的力学性质沿竖向呈水平成层变化,沿横向均匀无限延伸,将地震激励考虑为垂直向上入射的剪切波.按照此模型分析,土层地震反应分析实际即为一维波动问题.由于该模型形式简洁,物理意义明确,至今依然是场地地震反应分析的一种重要途径(Zalachoris,Rathje,2015).
常用的一维土层地震反应分析方法主要包括频域和时域两类方法.频域法以等效线性化方法为代表,最早由Idriss 和Seed (1968)提出.该方法将不同应变水平下的剪切模量和阻尼比以一个等效剪切模量和阻尼比代替,从而把非线性问题转化为线性问题并在频域内求解.廖振鹏(1989)根据等效线性化方法开发出了土层地震反应分析计算程序LSSRLI-1,在实践中得到了广泛认可.近年来,袁晓铭等(2016)采用直频法动剪模量阻尼比求解技术,提出了新一代土层地震反应分析方法,克服了传统方法低估软弱场地和深厚场地放大效应的缺陷.孙锐和袁晓铭(2021)提出了全局等效剪应变的概念和算法,建立了一种新的等效线性化分析方法.然而,等效线性化方法尚存在一些缺点,比如无法反映土层真实的受力状态(王志良,韩清宇,1981;栾茂田,林皋,1992),且忽略了较多的高频成分(齐文浩,薄景山,2007).为了解决上述问题,发展出了土层地震反应分析的时域方法,可以真实地反映土层在地震作用下的表现.丁海平和周正华(1998)提出了一维土层地震反应分析的时域有限元解法,并指出时域算法能够达到与频域算法相同的计算精度,但其计算耗时远少于频域算法.然而传统有限单元法由于形函数阶次较低,通常需将每个波长内布置6—10 个单元(廖振鹏,2002)才能准确刻画出波场特征,在土层复杂或地震动高频成分较丰富的情况下可能会需要较大的计算工作量.对此,邢浩洁等(2017)提出了分析成层场地地震反应的切比雪夫(Chebyshev)谱元法,仅需划分少量单元即可获得较高的计算精度.但其在计算切比雪夫谱单元质量矩阵时沿用了传统谱元法的做法,即利用切比雪夫多项式的性质获得单元质量矩阵的解析解,由此导出的质量矩阵为非对角形式,无法充分发挥显式时间积分算法的高效率优势.
本文在邢浩洁等(2017)的工作基础上,拟通过节点积分法(Fried,Malkus,1975)建立集中质量切比雪夫谱单元,解决传统切比雪夫谱元法由于需要对质量矩阵求逆而造成计算效率不高的问题,同时避免传统的质量集中方法的随意性,如行和集中法(Zienkiewiczet al,2013)或对角元素放大法(Hintonet al,1976).在该集中质量切比雪夫谱单元模型中嵌入多次透射人工边界(multi-transmitting formula,缩写为MTF)(Liao,Wong,1984),结合中心差分形成一种求解一维土层波动问题的高阶显式算法.并利用日本Kik-net 强震观测台网提供的井下和地面实测记录,以检验本文方法的适用性.
1 水平成层场地的集中质量切比雪夫谱元模型
1.1 水平成层场地简化模型

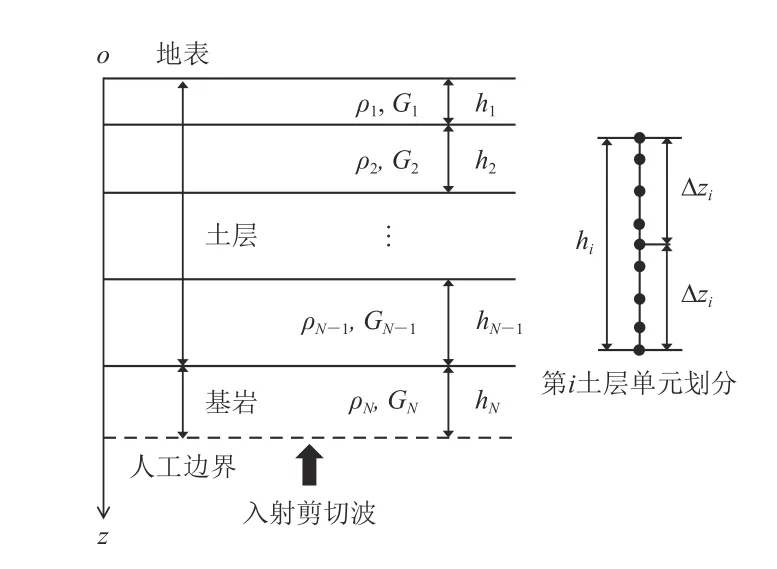
图1 水平成层场地切比雪夫谱元模型Fig. 1 Chebyshev spectral element model of horizontal layered soil site

1.2 切比雪夫谱单元位移模式
一维土层分析的切比雪夫谱单元以 [ −1,1 ] 区间内不等间距分布的高斯-洛巴托-切比雪夫(Gauss-Lobatto-Chebyshev,缩写为GLC)节点为参考单元节点,它们是第一类切比雪夫多项式的极值点.对于n阶切比雪夫谱单元,GLC 节点的位置为ξi=−cos(iπ/n),i=0,1,···,n.
设单元位移模式为

式中,Tk(ξ)为k阶第一类切比雪夫多项式,其表达式为Tk(ξ)=cos(kcos−1ξ),ci和ck为多项式系数,当i=0 或n时,取值为2,当i=1,···,n-1 时,取值为1.
1.3 切比雪夫谱单元特性矩阵
利用切比雪夫谱单元对水平成层场地模型进行空间离散后,得到离散方程

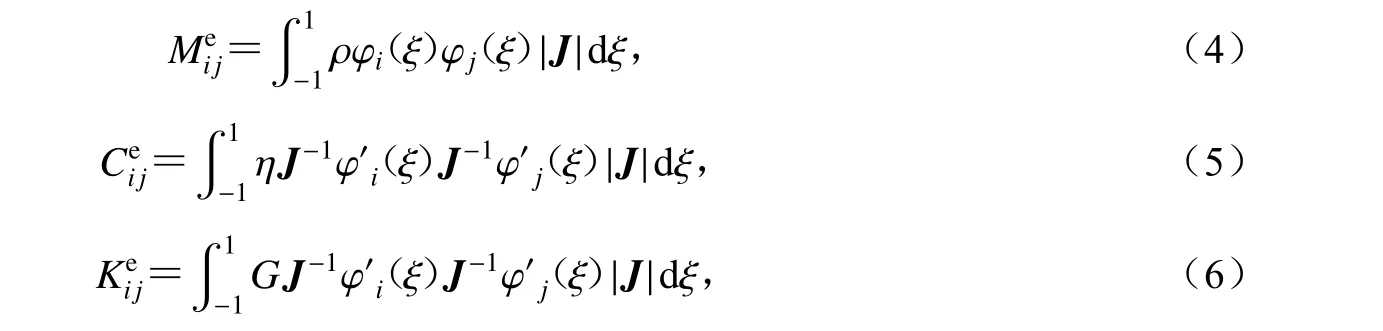
式中ρ,η和G分别表示土体的质量密度、阻尼系数和剪切模量, |J|为雅可比矩阵的行列式.对于一维谱单元,雅可比矩阵仅包含一个元素,即J=Δz/2,Δz为物理单元的长度.
为了建立集中质量矩阵,本文采用节点积分法求解单元质量矩阵,即以单元节点作为数值积分点,利用高斯-洛巴托(Gauss-Lobatto)数值积分计算单元质量矩阵的积分(式(4)).由于拉格朗日形函数具有克罗内克(Kronecker-δ)性质,由此导出的质量矩阵仅有主对角元素非零,其余非对角元素全部为零.单元GLC节点对应的高斯-洛巴托积分权系数为
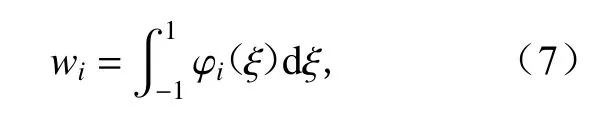
式中:wi为与节点ξi相对应的积分权系数;φi(ξ)为式(2)中的单元形函数.1—5 阶切比雪夫谱单元的GLC 节点位置及对应的积分权系数,列于表1.
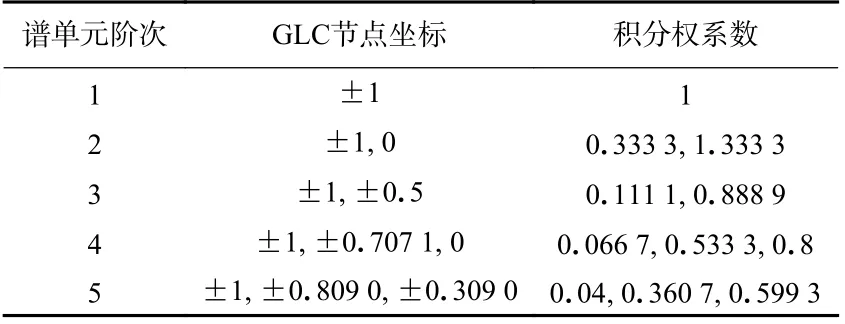
表1 GLC 节点上的高斯−洛巴托积分权系数Table 1 Gauss-Lobatto quadrature weights based on GLC points
利用式(7)的数值积分格式计算式(4)单元质量矩阵,则质量矩阵的非对角元素全部为零,主对角元素可进一步计算为

2 时域逐步积分
对于土层地震反应分析问题,一般将入射波作为边界处的运动形式施加,因此需要将模型内域节点和边界节点分开处理.在本文建立的水平成层场地谱元模型中,边界节点仅有一个,即模型底部人工边界上的单元节点,其余节点均属于内域节点.将式(3)中的矩阵和向量按照内域和边界进行分块,得

一般情况下质量矩阵MI为对角阵,而阻尼矩阵CI通常不会呈对角矩阵形式,故由MI与CI组合的矩阵亦会是非对角阵.此情形下可考虑构建仅同质量矩阵呈比例的瑞雷阻尼矩阵,或者将阻尼矩阵对角化(Thomsonet al,1974)等措施.
3 基于透射边界的地震动输入
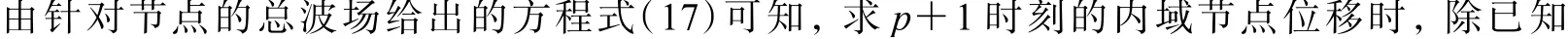
图2 切比雪夫谱单元的一阶MTF 插值方案Fig. 2 Interpolation scheme for first-order MTF in Chebyshev spectral element


4 算例分析
4.1 均匀半空间土体地震反应分析
为了检验本文方法的正确性,首先对一个均匀半空间场地模型进行分析,根据行波理论得到其解析解.该模型土体厚度为180 m,土体质量密度为2 000 kg/m3,剪切波速为250 m/s.底部设置一阶MTF 人工边界,垂直向上输入幅值为1 m、主频为2 Hz 的雷克(Ricker)波位移脉冲.将整个模型划分为8 个4 阶谱单元,则单元尺寸约为输入波最短波长的一半.图3 显示了土层底部和地表的位移反应时程,其中底部反应时程的第一个波峰为入射波,第二个波峰为地表反射波.由图可知,入射波从底部传至地表时间约为0.7 s,与解析解吻合,同时,地表位移反应峰值等于入射波峰值的2 倍,符合自由地表条件.此外,地表未出现模型底部反射而来的地震波,说明MTF 人工边界条件成功实现.本例表明集中质量切比雪夫谱元法能够处理土层地震反应分析问题,而且在网格较为稀疏的情况下依然能够获得较高的计算精度.
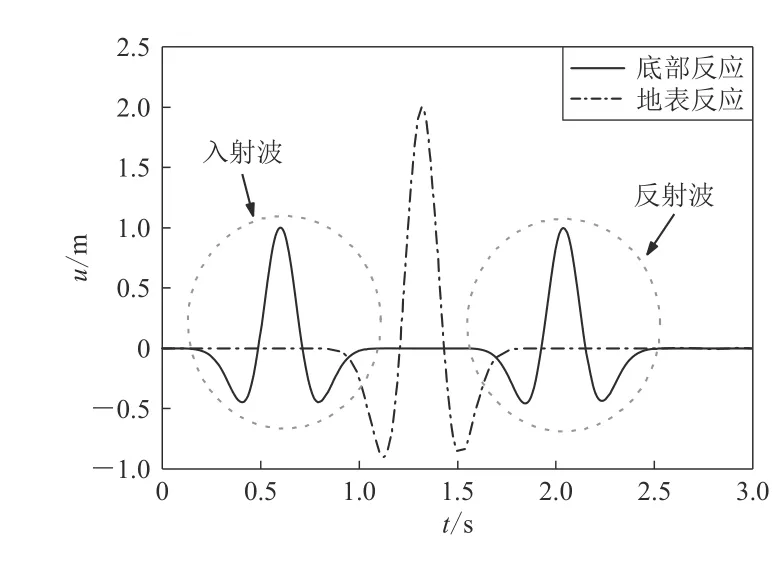
图3 均匀半空间模型在雷克波入射下的地表和底部位移反应Fig. 3 Displacement responses of ground surface and bottom of a homogeneous half-space model under Ricker wave incidence
4.2 Kik-net 台站记录模拟
利用日本Kik-net 强震观测台网(NIED,2021)提供的实测地震动记录和钻孔数据检验本文方法处理实际场地地震反应分析的能力.从Kik-net 台网中随机选取4 个具有代表性的台站,分别对应中国《GB 50011—2010 建筑抗震设计规范》(中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局,2010)所定义的Ⅰ1,Ⅱ ,Ⅲ和Ⅳ等四类场地.在每个台站中选择实测地面峰值加速度(peak ground acceleration,缩写为PGA)等于0.05—0.1g,0.1—0.2g和0.2—0.4g的EW 向或NS 向地震记录各一条,分别对应较弱地震动、中等强度地震动和较强地震动.以井下实测记录作为一维水平成层场地模型底部的基岩输入波,计算地表加速度反应并与地表实测加速度记录进行对比.由于Kik-net 数据库中未提供土体质量密度数据,本文利用Boore (2016)提出的公式根据P 波波速和剪切波速估算土体密度.各台站的土层剖面剪切波速如图4 所示,按照《GB 50011—2010 建筑抗震设计规范》计算得到的基本信息列于表2.
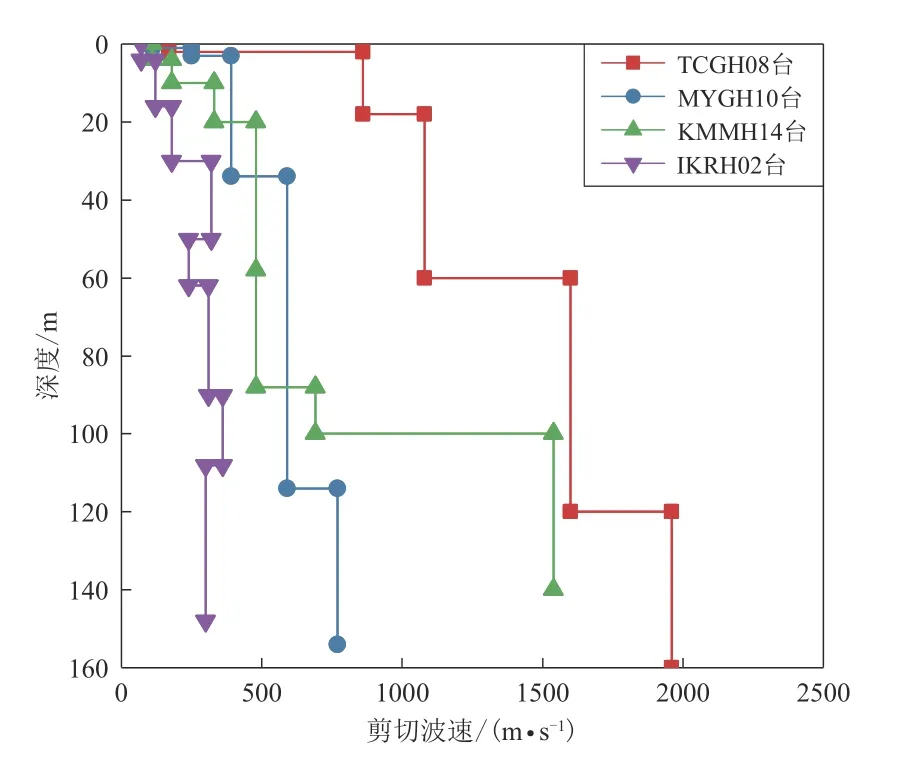
图4 四个Kik-net 台站的土层剪切波速图Fig. 4 Shear wave velocity profiles at the four Kik-net stations
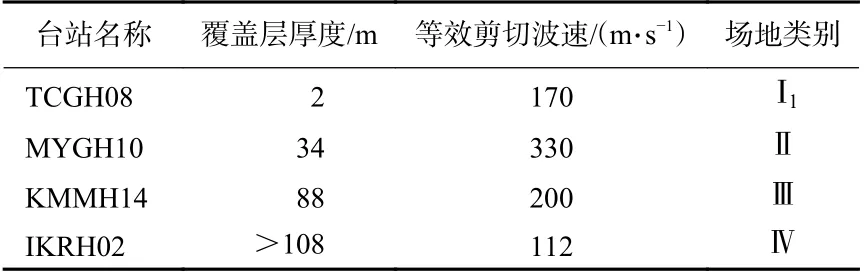
表2 选用Kik-net 台站的基本信息Table 2 Basic information of selected Kik-net stations
4 个台站在不同强度地震作用下地表的加速度时程反应,如图5 所示.可见,在多数情况下,本文方法计算得到的地表加速度时程与实测的地表加速度记录均能较好吻合.与输入的基岩实测加速度时程相比,所有台站的地表计算反应均显示出了土层的放大效应.即便对于IKRH02 台站这样覆盖层厚度超过100 m 的深厚场地,也依然体现出了土层的放大效应,未出现类似土层时域非线性软件DEEPSOIL 严重低估地表反应的问题(袁晓铭等,2016).
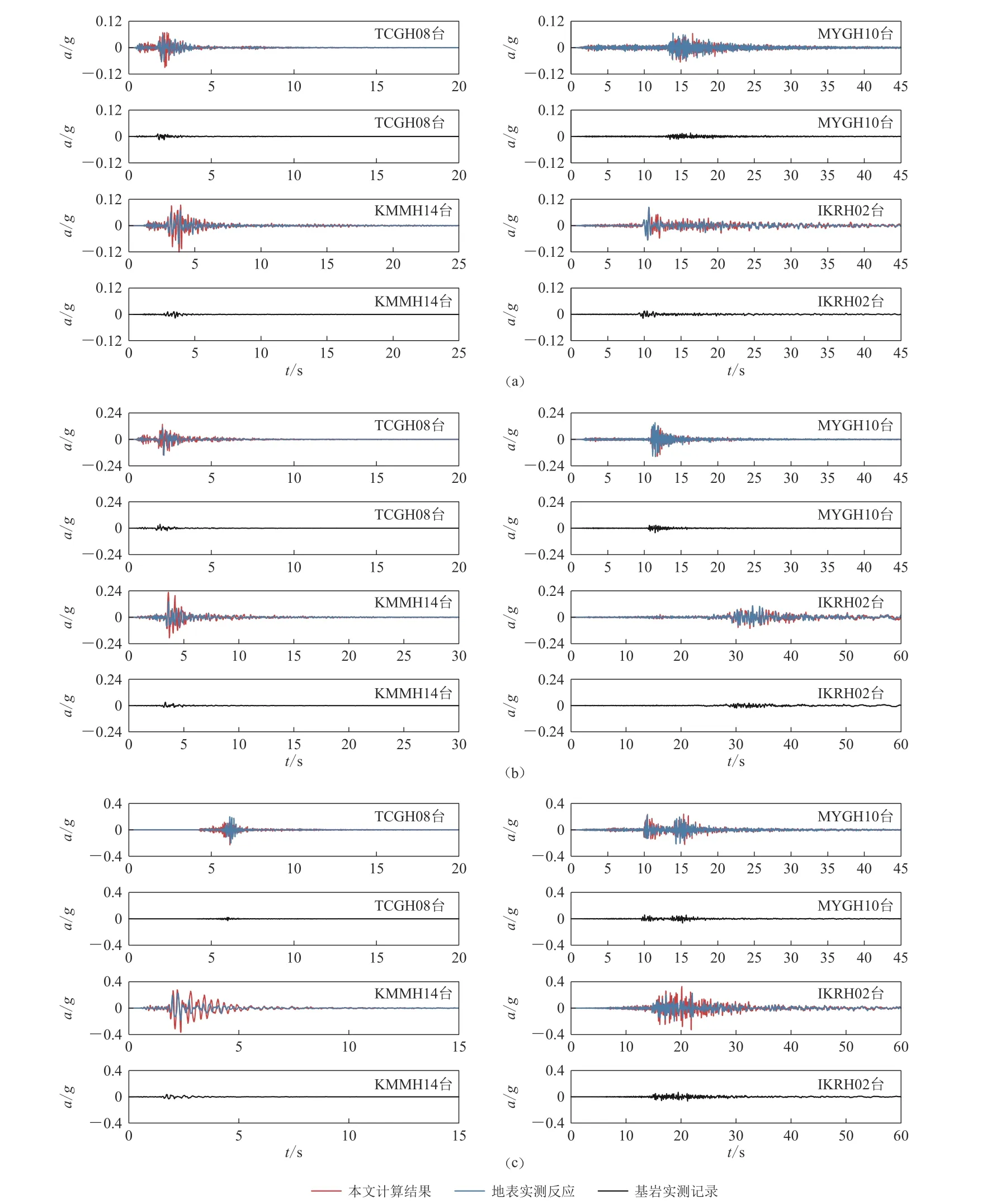
图5 不同强度地震动作用下四个台站地表加速度反应时程(a) 较弱地震动;(b) 中等强度地震动;(c) 较强地震动Fig. 5 Ground acceleration response histories of four stations under ground motions with different intensities(a) Weak ground motions;(b) Moderate ground motions; (c) Strong ground motions
表3 给出了按本文方法计算得到的PGA 与地震中实际记录PGA 的对比.由表中数据可知,对于Ⅱ类场地(MYGH10),本文预测PGA 最接近实际值,误差小于2.1%.但对于Ⅲ类场地(KMMH14),本文方法计算得到的PGA 大于实测值.总体而言,本文方法计算得到的PGA 总是稍小于或偏大于实际值,而未出现严重偏小的情况.表4 列出了本文计算得到的PGA 放大倍数及实际测得的PGA 放大倍数.所选台站的实测放大倍数介于3.28—7.40 之间不等,而计算放大倍数在3.67—10.48 之间不等.对于Ⅰ1类场地(TCGH08)、 Ⅱ 类场地(MYGH10)和Ⅳ类场地(IKRH02)在小震和中震情况下本文方法得到的PGA 放大倍数均与实测值相差不大,但在大震情况下本文结果偏大.

表3 不同强度地震动作用下各台站计算PGA 与实测PGA 对比Table 3 Comparison of computed PGA and recorded PGA for the stations under ground motions different intensities
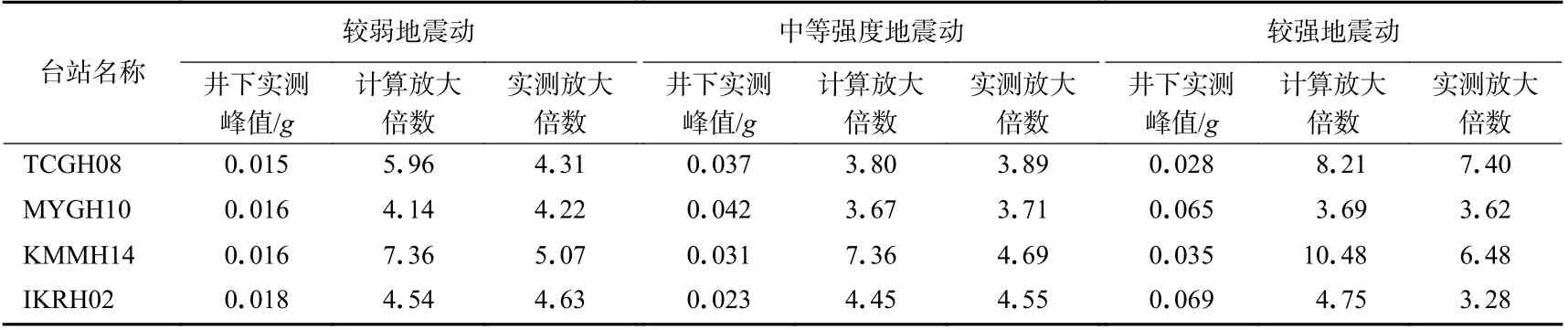
表4 不同强度地震动作用下各台站PGA 放大倍数Table 4 Amplification factors of PGA for the stations under ground motions different intensities
图6 为4 个台站在不同强度的地震作用下的地表加速度反应谱,阻尼比按5%计算.总体而言,本文计算反应谱在低频段(周期>0.5 s)与实测记录的反应谱较为接近.观察图6 可知,在较弱的地震作用下,Ⅰ1和 Ⅱ 类场地的反应谱峰值与实测记录相近,而Ⅲ和Ⅳ类场地的反应谱形状与实测值吻合,其中Ⅳ类场地的计算反应谱曲线与实测反应谱十分接近.在中等强度地震作用下,Ⅰ1和Ⅳ类场地的反应谱峰值与实测记录较为吻合.在较强地震作用下,本文计算反应谱曲线的形状大致与实测记录得到的反应谱一致,但对于Ⅲ和Ⅳ类场地计算得到的反应谱峰值比观测结果偏大.
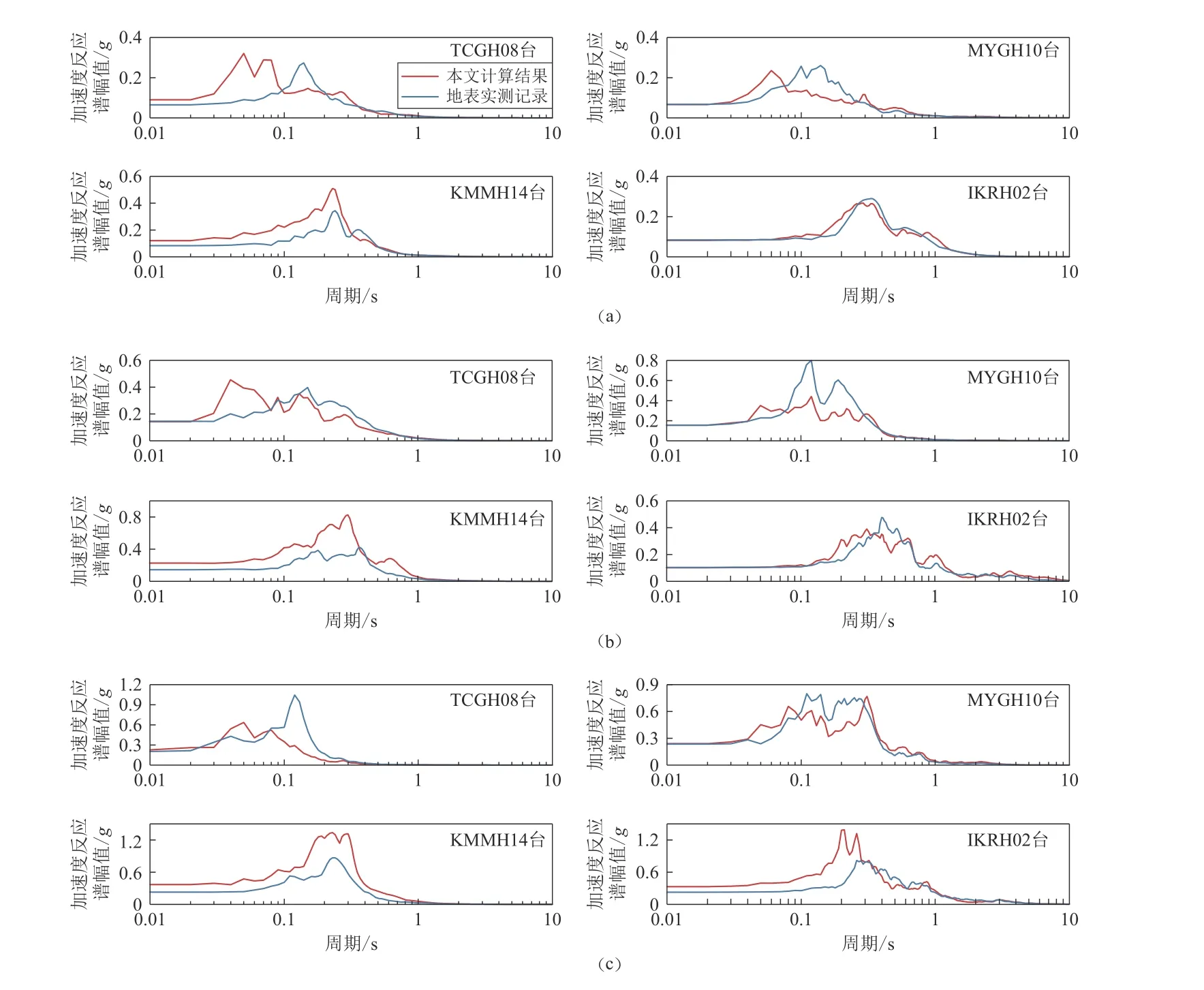
图6 不同强度地震动作用下四个台站的地表加速度反应谱(a) 较弱地震动;(b) 中强地震动;(c) 较强地震动Fig. 6 Ground acceleration response spectra of four stations under ground motions with different intensities(a) Weak ground motions;(b) Moderate ground motion; (c) Strong ground motions
造成本文计算结果与实际台阵记录存在一定差异的原因可能有:① 本文采用的一维水平成层场地模型是一种高度简化的计算模型,无法反映出实际三维场地的地形特征,因此一维波动的数值计算结果一般无法体现出对实际场地地震动有重要影响的地形放大效应;② 实际场地并不一定仅受剪切波作用,还有可能受到纵波、面波等多种地震波的作用,并且地震波的传播方向也不一定恰好垂直向上的;③ 本文方法未考虑土体的非线性特性.
5 结论
本文提出了一种求解水平成层场地地震反应的时域集中质量切比雪夫谱元法.通过节点积分法严格地导出集中质量矩阵,克服了传统切比雪夫谱元法由于质量矩阵为非对角矩阵形式所带来的计算效率不高的问题.采用中心差分法进行时间积分,并嵌入多次透射人工边界,形成了高效的时域显式算法.与传统有限单元法相比,该方法在每个波长内仅需布置一个谱单元即可获得令人满意的计算精度,显著降低了对空间网格尺寸的要求.
选择日本Kik-net 强震台网中分属四种不同场地类型的台站记录检验了本文方法处理实际场地的能力.计算结果表明,本文方法对于Ⅰ1,Ⅱ和Ⅳ类场地在较弱地震和中等强度地震作用下能够较好地预测地面运动特征,但对于Ⅲ类场地及强震作用下的地表反应计算结果与观测结果相比仍存在一定误差,后续工作中可考虑添加土体的时域非线性本构关系.
