边坡稳定分析方法综述

2022-03-31刘琦

建筑与装饰 2022年6期

刘琦

中铁二十一局集团有限公司甘肃兰州 730000

引言

我国是一个多山的国家，随着国民经济的发展，工商业及民用建筑剧增，许多工程边坡的分析方法不断产生。此外，尾矿坝、堆渣坝的坝体也会形成许多高边坡。在建设中开挖和堆填的边坡数量很多，高度很大。由于地质条件复杂，边坡工程是一个很复杂的系统工程，其失稳造成的灾害、事故常常发生，造成重大的生命财产损失。因此，如何在复杂地质条件下分析清楚边坡稳定并做好防护，一直都是工程学术界极为重要的课题。本文全面而又系统地对边坡稳定性目前采用的分析法做出分类，同时分析了各自的基本原理及其优缺点。为合理有效地在复杂地质条件下对边坡稳定性分析方法选择提供依据，同时为下一步对边坡稳定性研究理清思路[1]。

1 定性分析

该方法在大量收集各类边坡所在区域的资料基础上，综合考虑边坡稳定的影响因素，通过工程地质类比或图解分析等方法，对边坡稳定情况和发展走势作出估计及预测。目前工程用到的定性分析法主要有以下几类。

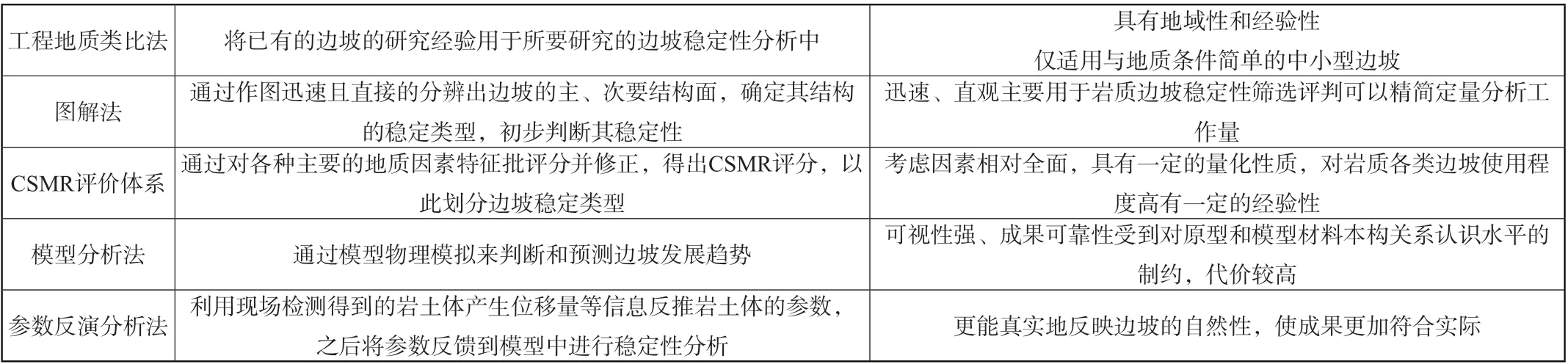
表1 边坡稳定定性分析法类比表

尽管定性分析注重对建筑边坡自然性认识，综合考虑了影响稳定性的各种因素且能迅速对其稳定性和未来发展趋势做出推测，但是不考虑边坡内应力和强度关系，其变形能力之间矛盾且经验性强无数量界限。目前此类方法使用已经不断减少。

2 定量分析

边坡稳定常采用定量分析法，包括极限刚体平衡法、数值分析法和可靠度法等，极限刚体平衡法因其物理性能和力学上较清晰的概念、计算简便为工程界广为采用、接受，是传统且经典的定量分析法[2]。

3 极限刚体平衡法

极限刚体平衡法主要是针对滑动型失稳模式。崩塌破坏模式的极限平衡分析法尚不成熟，主要依据力矩平衡条件求解。当前常用的极限刚体平衡分析方法主要是针对二维、三维与楔形体稳定求解。但是，由于三维方法往往繁复耗时，且滑面须在二维基础上选定，尚缺乏搜索优化功能，其推广受到很大程度上的限制，有待发展。对于一般的边坡工程，二维分析成果已能满足工程应用要求，仅有对于空间效应明显且规模较大的边坡工程才在二维的基础上展开三维计算分析。因此，下面进对二维刚体极限平衡法做介绍。

3.1 二维刚体极限平衡法

该方法是在工程实践应用中较早、较经典的定量确定性方法，是目前常用到的分析方法。尽管该方法均有力学假设并且依托一定的工程实践经验，得到的结果为近似解，但是其模型简单，公式的计算较简捷，可以解决许多复杂剖、断面和各种加载形式。因此，到现在其应用仍十分广泛。

二维刚体极限平衡法可分为两类：非严格条分法： Bishop简化法、Sarma法、Janbu简化法、瑞典法、不平衡推力法等；严格条分法：Morgenstern-Prince法、Spencer法等。其中Spencer法是Morgenstern-Prince法的特例。各种方法的比较见下表。

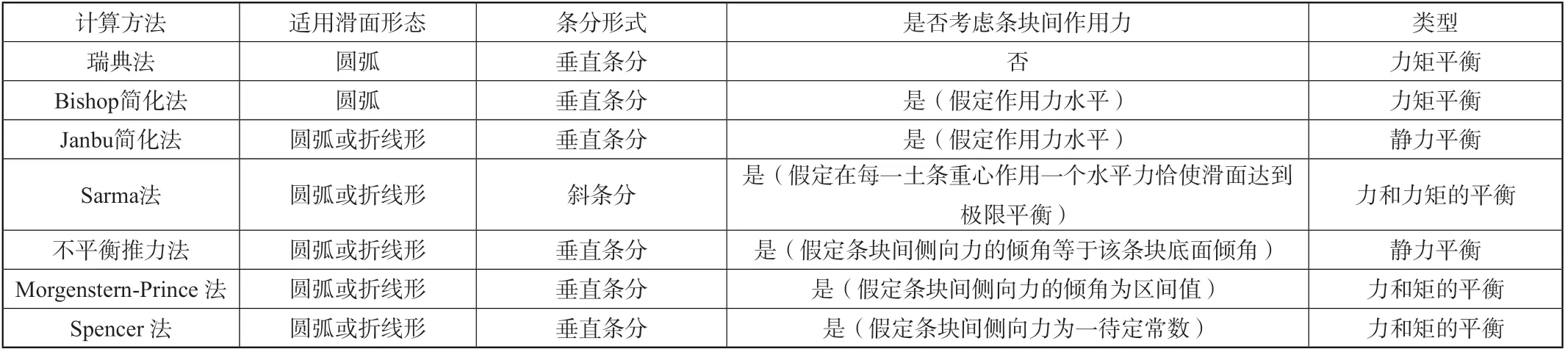
表2 二维刚体极限平衡法的比较

3.2 数值模拟分析法

此方法主要用于有限变形的失稳情况。一般可分为两类：第一类是基于连续介质数值分析的方法；第二类主要用于非连续物质的分析方法。其用各类数值分析耦合，比如有限元法和边界元耦合、边界元和离散元耦合等，此类方法目前也开始应用于计算边坡工程。

数值模拟分析常用于考虑岩土土体自身的应变、应力间关系，对平衡极限不考虑如岩体等自身应力、应变关系，为边坡稳定提供了新的分析办法。但它还是不能够较好的求大变形与位移不连续的问题。对无限区域和集中应力区域的求解不够准确，对岩土滑动位置不能直接计算其对应的安全系数值，且计算软件分析所需的信息和参数较多，对技术员技术能力要求较高[3]。

3.2.1 基于连续介质的数值分析法。目前，边坡稳定性分析中常用的有限元方法有圆弧搜索法和强度折减法。有限元圆弧搜索法遵循极限平衡法的思想，但假定滑动裂纹表面上的滑动力和抗滑力是通过有限元计算精确确定的。强度折减法是指在有限元计算中不断减少土的强度参数。当计算不收敛时，将折减系数作为边坡稳定安全系数。强度折减法的一个主要特点是不需要预先假定滑动面。从目前的应用来看，它是一种很有前途的边坡稳定性分析方法。

3.2.2 基于非连续介质的数值分析法。基岩是一种具有复杂材料特性的不连续材料，因此有一些数值分析方法可以处理这种不连续材料。基于离散单元的非连续变形分析方法非常适合处理非连续节理岩体。由于忽略了岩体的变形过程，无法模拟裂隙的产生和失稳过程。此外，应用流形中的有限覆盖法建立流形法，从数学上解决了连续和不连续材料计算中近似函数的统一结构等一系列问题，使连续变形和非连续变形的统一计算分析成为可能，并能分析岩体裂隙、岩土滑移等相似特征。

3.3 可靠度法

可靠度法是将边坡岩土的稳定问题视为一个随机发生的过程，将影响岩土稳定的各类因素看作随机变量，采用概率论分析法和可靠度描述岩土边坡稳定情况。与传统确定性理论相比，可靠度法对边坡稳定安全系数数值的各个影响因子均根据其不确定性给以一定的考虑，才能更好反映岩体的实际状态，合理解释众多用确定性理论不能很好解释的问题。但在实际使用中仍较少的采用可靠度分析这一评价法，受制约因素体现在与当前规范的协调标准、配套取值，及概率与可靠度分析等需大量的试验数据确定变量的数值、分布，时间及费用投入较多。

3.4 极限分析法

极限分析法的基础是极限分析的极限定理，即上、下限定理。采用极限分析法在结构力学分析中采用了部分的简化，其所得结果有可能不是真实反应，有时还会出现较大误差，对于复杂的土层结构，计算上较难。随着计算机技术的发展，数值方法求解边坡稳定特别是上、下限解决问题成为非常活跃的方向。由于它不仅可以避免非线性计算，跟踪实际加载路径逐渐增加，而且可以直接计算极限荷载和安全系数的问题，因此在岩土结构和边坡的稳定性评价中得到越来越广泛的应用。

3.5 广义极限法

基于虚功方程的广义极限平衡法，即在极限平衡法的基础上，再应用屈服函数的极值条件，可以消去安全系数，使得在不必对土体的受力进行简化的条件下，获得安全系数。同样可以对任意可能的滑动面进行试算，找出适用的计算方法。

与通常的极限平衡法相比，在不需要对土体的受力进行假定或简化的情况下，适用于任意的滑动面（极限平衡法只适用于特定平面和常用螺旋面），这无疑是一个很大的进步。但是同样，由于需要事先确定滑动面的形式，所以，广义极限平衡法所得到的结果一般也是安全系数的近似解[4]。

4 非确定性分析

非确定性分析是种有限的数据分析，且存在着很大的不确定。就使得确定性为指导性思想的传统边坡稳定性分析法，在实际的应用中无法取得令人满意的效果。近年来，随着科学的发展，技术的进步，以及边坡稳定性的深入研究，大家普遍知道在传统的边坡稳定性分析中，存在了太多的不确定因素。对此，国内外许多专家在分析边坡稳定性时都考虑了不确定性因素。近年来发展起来的主要分析方法有概率法、人工神经网络法、模糊综合评价分析法和灰色系统分析法等。

4.1 人工智能法

人工智能法采用计算机，充分利用了人类的经验，包括神经网络控制方法、遗传算法等，具有广阔前景。人工智能网络是一种非线性映射处理系统，其程序具有通用性，可用于岩土稳定性分析。遗传算法不需要函数连续性以及梯度信息要求，全局处理能力强，适合于复杂问题的并行处理和优化求解。本文还提出了一种适用于不确定情况的专家系统，能有效地考虑边坡组成材料参数的不确定性和发生变化。人工智能方法不能反映岩土的内应力，需要大量的现场实际测算数据。随着理论的完善和数据的积累，它将成为未来一种相对简单的技术方法，也可用于其他工程计算。

4.2 灰色系统法

灰色系统法认为，事物的决定因素中若有未知不确定的，又或有已知的，较为模糊的系统称为灰色系统。把系统中一切信息变量看作灰色变量，用特定的方法建立起用来论述这种灰色变量的数字模型。利用灰色变量关联度之间的分析原理，确定岩土稳定性计算中，各个影响因素的影响度大小，进而用多种因素叠加起来分析评估岩土的稳定情况。该方法所得的结果基本上和边坡实际状态一致，并且此方法较为简单直观，可操作性也较强。但其内在力学理论不够清晰、明确，缺少定量描述[5]。