一类高阶椭圆型方程特征值的多项式特解法

张姊同，曹艳华，朱挺欣

一类高阶椭圆型方程特征值的多项式特解法

张姊同，*曹艳华，朱挺欣

（华东交通大学理学院，江西，南昌 330013）

通过给出一种求解高阶椭圆型偏微分方程特征值的多项式特解法，使用多项式特解作为基函数对2阶、4阶、6阶和8阶椭圆型偏微分方程进行求解，同时采用多尺度技巧降低系数矩阵的条件数，得到了稳定的数值解。数值算例表明该算法在求解高阶偏微分方程特征值问题时具有精度高、效果好等方面的优越性，进一步证明了多项式特解法具有较高的精度和良好的稳定性。

高阶椭圆型偏微分方程；特征值：多项式特解法；

0 引言

在工程领域，椭圆型偏微分方程特征值问题有广泛的应用，用于求区域的Poincare常数[1-2]的Laplacian特征值问题，复杂非线性方程谱理论中的特征值问题等[3]，在融合实验中的等离子物理学。天体物理学、流体流动的线性稳定性力学等也有广泛应用[4]。求解偏微分方程特征值上通常采用有限差分法(FDM)[5-6]和有限元法(FEM)[7-8]等，然而这些传统的方法在计算规模较大问题时，产生了需要对网格进行剖分、计算耗时长、增加计算成本等缺点。基于径向基函数的无网格方法在求解线性偏微分方程中的应用非常宽泛，例如Kansa方法。而特解法是在Kansa方法的基础上发展而来的，在这种方法中，把给定的函数在偏微分方程中的特解作为基函数去近似数值解[9]，而不再直接作为基函数，和Kansa法相比，特解法的数值结果更精确有效，但其有着径向基函数形状参数不确定的问题。

采用多项式特解作为基函数的特解法(MPPS)[10]求解高阶椭圆型偏微分方程的特征值问题，基于多项式特解的基函数形状参数是确定的，解决了上述问题，使特解法更精确，更易于实现。该方法有计算格式简单，配置节点灵活的特点，因此可以应用于高维的规则区域和不规则区域，是求解偏微分方程的有效方法[11-12]。考虑如下特征值问题：

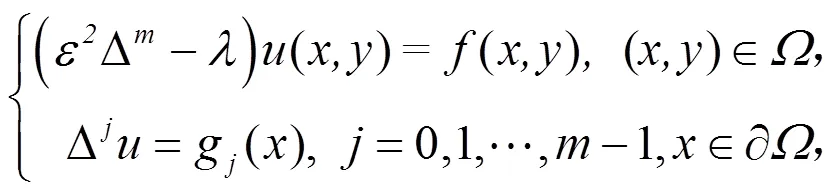
1 多项式特解法

本节简要介绍多项式特解法求解偏微分方程的步骤。考虑下面偏微分方程的边值问题：

其中：

利用最小二乘法求得方程组(6)的最小二乘解，得到：

定理1.1[10]对于如下常系数二维二阶偏微分方程的一般形式，给出了求解偏微分方程的步骤：

证明 式(7)可以写成：

综上有：

联立式(10)和式(13)，有以下等式成立：

2 数值结果

文章所有的插值点都是由蒙特卡罗方法生成的随机点[13]，此外，文章使用的多尺度技巧是一种预处理技巧[14]，减小了多项式特解法生成矩阵的条件数，使得多项式基函数在多项式基函数阶数变大时是稳定的。

式(18)的解析解为：

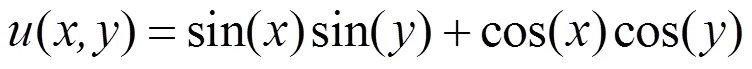
本文的数值例子均考虑规则的单位方形区域，其参数方程式如下：

单位方形区域的剖面图如图1所示。

算子

内点、边界点和测试点的数目分别为3000个、600个和441个，这些点是随机分布的。

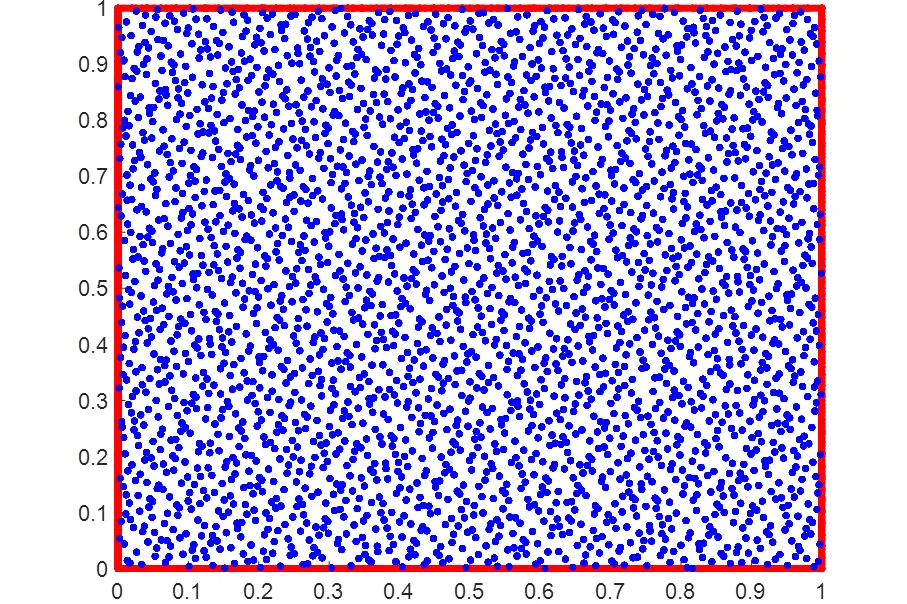
图1 计算域剖面图

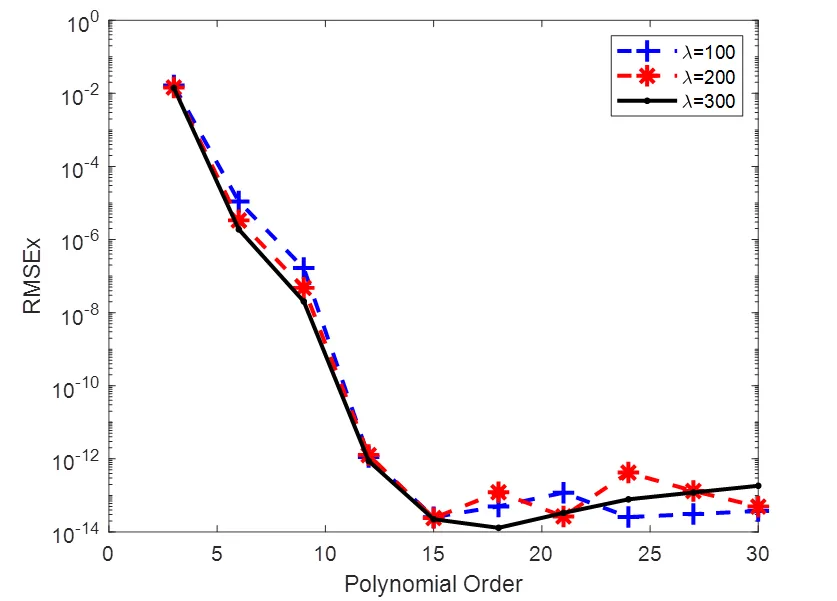
图2 不同误差对比图

图3 使用多尺度技巧和不使用多尺度技巧的误差图

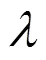
表1 2阶椭圆型方程在不同阶数多项式基函数下的不同的对比

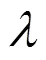
图4 不同λ误差对比图

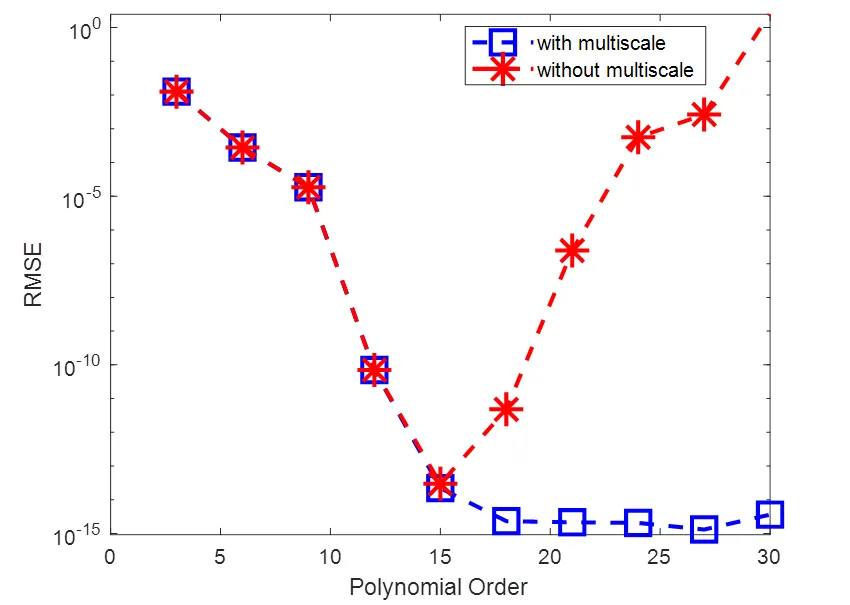
图5 使用多尺度技巧和不使用多尺度技巧的误差图

表2 4阶椭圆型方程在不同阶数多项式基函数下的不同的对比

式(20)的解析解为：

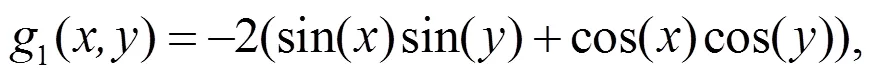
图6 不同误差对比图

图7 使用多尺度技巧和不使用多尺度技巧的误差图

表3 6阶椭圆型方程在不同阶数多项式基函数下的不同的对比

式(21)的解析解为

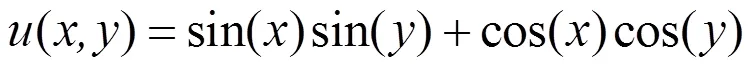
算子

图8 不同误差对比图

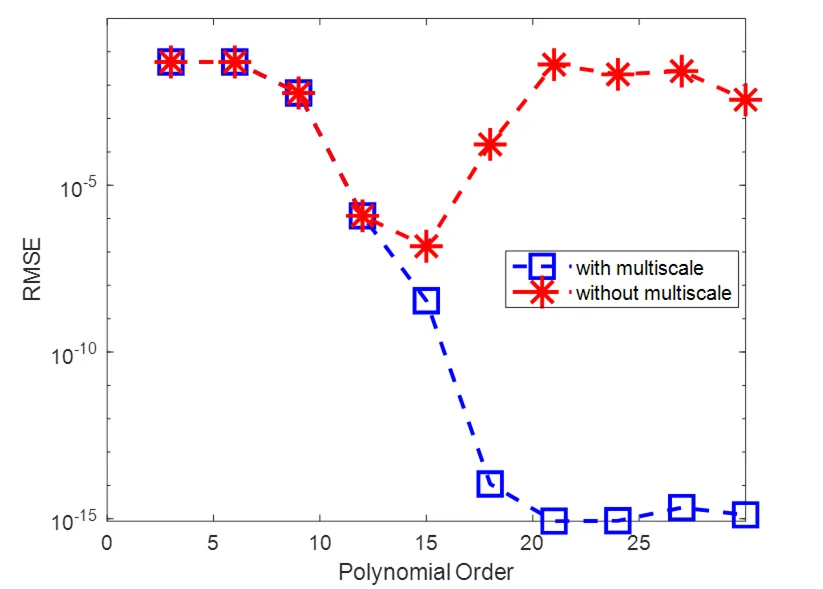
图9 使用多尺度技巧和不使用多尺度技巧的误差图

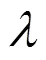
表4 8阶椭圆型方程在不同阶数多项式基函数下的不同的对比

图10 参数，时不同m的误差对比图

3 结论

本文验证了多项式特解法求解高阶椭圆型偏微分方程特征值问题的有效性，得到了较高的精度和很好的稳定性，进一步证明了该方法可以推广到更高阶、更复杂的椭圆型偏微分方程的特征值问题，或者高阶偏微分方程的边值问题等。与其他经典的求解特征值问题的数值方法相比，多项式特解法有以下优点：

1）多项式特解法把偏微分方程中给定函数的特解作为基函数去近似数值解[9]，而不再直接作为基函数，使得到的数值结果和Kansa法相比更精确；

2）多项式特解法使用基于多项式特解的形状参数确定的基函数，解决了特解法中径向基函数形状参数不确定的问题，和特解法相比更易于实现，数值结果更稳定；

3）多项式特解法的精度和稳定性都极好，易于编程，计算速度很快；

4）多项式特解法对求解高维复杂不规则域的偏微分方程是十分有效的。

[1] Kikuchi F, Liu X. Estimation of interpolation error constants for the P0 and P1 triangular finite elements[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(37-40): 3750-3758.

[2] Sebestova I, Vejchodsky T. Two-sided bounds for eigenvalues of differential operators with applications to friedrichs, poincaré, trace, and similar constants[J]. Siam Journal on Numerical Analysis, 2013, 52(1): 308-329.

[3] Plum M. Explicit H2-estimates and pointwise bounds for solutions of second-order elliptic boundary value problems[J]. Journal of Mathematical Analysis and Applications, 1992, 165(1): 36-61.

[4] Grebenkov D S, Nguyen B T. Geometrical structure of Laplacian eigenfunctions[J]. Siam Review, 2012, 55(4): 601-667.

[5] Kuttler J R. Direct methods for computing eigenvalues of the finite-difference laplacian[J]. Siam Journal on Numerical Analysis, 1974, 11(4):732-740.

[6] Tao L, Liem C, Shin T. A fourth order finite difference approximation to the eigenvalues of a clamped plate[J]. Journal of Computational Mathematics, 1988, 6: 267-271.

[9] 刘燕山.无网格特解法求解非线性椭圆方程[D].成都:电子科技大学,2018.

[10] Dangal T R, Chen C S, Lin J. Polynomial particular solutions for solving elliptic partial differential equations[J].Computers and Mathematics with Applications, 2017, 73: 60-70.

[11] Cao Y H, Kuo L H. Hybrid method of space-time and Houbolt methods for solving lineartime-dependent problems[J]. Engineering Analysis with Boundary Elements, 2021, 128: 58-65.

[12] Cao Y H, Chen C S, Zheng H. Space-time polymial particular solutions method for solving time-dependent problems[J]. Numer Heat Transf Part B: Fundam, 2020, 77(3): 181-194.

[13] 曹艳华,李楠,张姊同,等,一维分方程的多项式特解方法(英文)[J]. 应用数学, 2020, 33(2): 295-307.

[14] Liu C S. A multiple-scale trefftz method for an incomplete cauchy problem of biharmonic equation[J]. Engineering Analysis with Boundary Elements,2013, 37(11): 1445-1456.

POLYNOMIAL PARTICULAR SOLUTIONS FOR SOLVING EIGENVALUE PROBLEM OF A CLASS OF HIGHER ORDER ELLIPTIC EQUATIONS

ZHANG Zi-tong,*CAO Yan-hua, ZHU Ting-xin

（School of Sciences, East China Jiaotong University, Nanchang, Jiangxi 330013, China）

The paper presents a method of polynomial particular solutions (MPPS) for eigenvalue problem of higher order elliptic partial differential equations. The second, fourth, sixth and eighth order elliptic partial differential equations are solved by using the polynomial particular solutions as the basis function, while the condition number of the coefficient matrix is reduced by using the multiscale technique, and a stable numerical solution is obtained. Numerical examples show that the algorithm has the advantages of high accuracy and good effect in solving eigenvalue problems of high-order partial differential equations, it is further proved that the polynomial particular solutions have high accuracy and good stability.

higher order elliptic partial differential equations; method of polynomial particular solutions; eigenvalue problem; innovation ability

1674-8085（2022）02-0008-07

O241.82

A

10.3969/j.issn.1674-8085.2022.02.002

2021−11−01；

2021-12-11

国家自然科学基金项目(11461026)；江西省研究生创新资金项目(YC2020-S313)

张姊同(1997-)，女，吉林长春人，硕士生，主要从事微分方程数值解方面的研究(E-mail:Z15797676772@163.com)；

*曹艳华(1978-)，女，山东兖州人，副教授，博士，主要从事微分方程数值解方面的研究(E-mail:yanhuacao@yeah.net).