法律证据事实的逻辑方法探析

杜文静 刘海

长期以来，我国司法界坚持“以事实为依据，以法律为准绳”的口号作为司法审判的指导原则。有学者如陈波从认识论层面上对证据与事实的概念做了细致的分析，并提出“以证据为依据，以法律为准绳”的新口号来替代传统的口号。（[26]）舒国滢和宋旭光肯定了陈波对事实概念之复杂性与使用困境的分析，但认为其提出的新口号略有不妥，值得商榷。他们认为，似乎更为妥当的说法应当是“司法裁判以事实为根据，事实认定以证据为根据”。（[31]）后来，陈波又对舒国滢和宋旭光的商榷进行了回应，坚持自己之前的主张，并扩充为“以审判程序为中心，以证据为依据，以法律为准绳”，他认为这个口号应该成为司法审判的指导原则。（[27]）实际上，陈波与舒国滢和宋旭光的观点存在共同之处，他们都在关注证据与事实的联系和区别，并从哲学意义上进行了详细论述。本文将从方法论的维度来阐述证据与事实的关系，并揭示其背后的逻辑基础。

司法证明活动涉及用观察到的证据及一般的常识知识进行推理，以帮助办案人员确保事实认定的准确性。张保生指出：从法庭认识论角度来研究事实认定，应当打破“心证”不可言传的神话，将其看作是事实认定者在头脑中重建过去事实的信息加工过程，是通过“证据之镜”对实际上发生了什么进行经验推论的探究过程。事实认定与经验推论有相同的内涵和外延，都是指“结论达成的过程；从证据到证明的思维过程”，并构成一个从证据到推断性事实和要件事实的推论链条。（[34]）文献表明，从证据到事实的推理过程存在三种主流的建模方法，即论证、故事和概率模型。（[21]）这三种方法都指明了人们应当如何分析证据并且最佳结构化这些证据，从而合理地构建案件事实。它们的逻辑基础是一种最佳解释推论（Inference to the Best Explanation，简称IBE）。最佳解释推论是一种新兴事实推理方法，不同于传统的法律推理。谈及法律推理，人们头脑中最初的表象也许是公式化的“法律规则+案件事实=判决结论”。然而，最佳解释推论是基于“知识以及经验的概括+证据=案件事实”的推理形式，是法律逻辑在新时代背景下的更新和拓展。由最佳解释推论断定的案件事实是一种解释性事实，其中包含着主体的理论前见，包含着主体价值取向、实践背景，包含着语言本身的局限和对既有概念框架的依赖性，因此并不具有纯粹客观性，但其在方法论上自行设定了三大自我要求：效度（validity）、信度（reliability）和精度（precision）。（[30]）

1 最佳解释推论

1.1 最佳解释推论的构成

最佳解释推论最初由哈曼（G.H.Harman，[7]）提出，后来诸多哲学家和法学家对此展开了深入研究，如利普顿（P.Lipton，[9]）、撒加德（P.Thagard，[19]）等。具体来说，它是指：“当有很多假设都能解释某一证据时，推论者在得到一个合理假设时，必须拒绝其他假设。因此，如果一个已知的假设相比于其他假设能为某个证据提供‘更好的’解释，那么该已知假设就是真的。”（[7]）在证据推理语境下，最佳解释推论的推理形式可概括如下：

1.E是已观察到的证据集合；

2.到目前为止，基于证据E可获得的潜在解释一共只有n项，H1,H2...,Hn分别是n项潜在解释中的解释性事实；

3.包含H1的解释是n项解释中的“最佳”；

4.因此，暂时性地接受事实H1。

由此可见，最佳解释推论的推理过程主要分为两个阶段。第一个阶段是形成潜在解释性事实，即事实发现者根据现已收集到的证据集合E，并结合关于世界的常识和经验知识，形成可以解释这些证据的各种潜在解释。人们也可利用这些潜在解释进行预测推理，预测可能存在其他的证据。一个潜在解释如果能成功的预测到某些新证据，那么它更值得信任，更具有似真性。搜寻并收集到这些预测的证据可以扩充到证据集合E，并初步检验这些潜在解释的似真性，排除明显不似真的潜在解释。假设到目前为止，一共生成了n项似真的潜在解释，对应解释性事实（假设性事实）为H1,H2,...,Hn。举例如下，在卧室发现一具男尸（E），对于这具尸体死亡的原因，可以形成三种解释：他是自然死亡（H1）；他被谋杀（H2）；他是自杀（H3）。

第二个阶段是评价和比较解释，需要依据一定的标准，从形成的所有解释中选出“最佳”解释，并排除其他竞争解释。挑选出来的最佳解释应当被视为暂时性接受。如果在未来某个时间点，新获得的证据加入证据集合E，则要重复第一、第二阶段的操作，重新确定最佳解释。这是一种循环认定的过程，直到此刻没有可获取的其它证据和潜在解释为止。因此，最佳解释推论也被刻画为可废止推理。判定何种解释是“最佳”？根据什么标准进行评估和比较？正是第二阶段关注的主要问题。哈曼认为“最佳”很难被精确地定义，但至少要包含如下要素：“哪种解释更简单、哪种解释更似真、哪种解释符合的信息更多、哪个解释有更少特设性假设。”（[7]）约瑟夫森夫妇（John Josephson and Susan Josephson）则主张，一个解释要被视为最佳，则它应当比其他选择更好地解释本案中的证据。在确定最佳解释时还需要考虑其他因素，例如，存在多少似真的竞争解释，当前解释优于这些解释的决定程度如何以及寻找其他选择的彻底程度如何。（[8]）不少疑问尚未有定论，评价解释并选出最佳解释的标准仍模糊不清，诸多观点需要进一步核实，其中备受争议的一种观点认为基于回溯推理的思想形成的解释性事实是一种最佳解释。

1.2 最佳解释推论与回溯推理迷雾之廓清

近年来，学界存在着把最佳解释推论和回溯推理相关联的倾向，有关最佳解释推论的理论及应用常常结合回溯推理进行讨论。回溯推理的思想肇始于古希腊智者学派，由哲学家皮尔士（C.Peirce）对其进行理论化并提出基本架构（[11]），推理形式如下：

1.E是已观察到的证据集合；

2.H是证据E出现的一个潜在解释性事实；

3.所以，H可能为真。

在哈曼看来，最佳解释推论与其他学者所谓的“回溯推理”“假设的方法”“假设推理”和“理论推理”都相似，并且最佳解释推论属于一种独立的非演绎推理。（[7]，第88-89 页）有学者指出：“回溯推理涉及到提出假说和确证假说，也涉及到寻求假说以及对假说进行具体的评价、甄别和确证。也就是说，它们是一种扩展和可废止的推理形式，实质上是同一类推理，即回溯推理是最佳解释推论的一种初始名称，最佳解释推论是回溯推理的现代表述和进一步的论证。”（[32]，第97 页）然而，撒加德却认为最佳解释推论和回溯推理不同，他主张：回溯推理只形成解释，而最佳解释推论评价这些解释。（[19]，第143 页）还有学者将最佳解释推论作了狭义、中义和广义的区分，认为：狭义的最佳解释推论相当于贝叶斯认证的似然推理；中义的最佳解释推论相当于贝叶斯条件化推理及其初始概率的确定；广义的最佳解释推论相当于决策推理，其接受规则相当于最大期望效用原则，所以它要么相当于贝叶斯推理，要么相当于决策推理，因而失去自己的独立性。（[33]，第22 页）

通过对照最佳解释推论和回溯推理的模式可以发现，回溯推理只形成解释，不评价和比较解释，因为在回溯推理的形式中没有提及其他可选择的解释。由此看来，撒加德的观点更为可取，回溯推理被狭义理解为生成假设，仅属于最佳解释推论的第一个阶段。而它缺失的阶段，正是最佳解释推论指引司法实践的各种调查和决策语境中进行证明的必要环节。所以，我们不能将其视为单个的推理步骤，而应当将它视为描述“假设性解释”的多个步骤之组合。证明过程中的这些步骤需要运用多种推理类型，这些推理类型可以构建解释、评价解释、比较解释并从中选择最佳解释，形成从证据到案件事实的最佳构建。正如帕尔多（M.Pardo）和艾伦（R.Allen）所言，司法证明的性质具有解释性，证据推理的过程本质上是一种最佳解释推论。（[10]）最佳解释推论涉及证明过程中运用的所有重要的推理步骤，至于如何比较不同解释，并选择某个具体解释作为对于已观察到证据的最佳解释，乃是一个重要而棘手的问题。在接下来的讨论，本文拟以证据推理的界定为起点，表明证据推理的三大方法如何解决该难题。

2 证据推理的意蕴

常言道“打官司就是打证据”，证据无疑是证明案件事实的基础。证据这一术语内涵丰富，为了运用最佳解释推论构建案件事实，它不仅包含证人证言、书证等证据材料，还应当包含基于该类证据材料推论出的命题。我们将其称为证据性事实，一般以假设或解释的形式提出。例如张某作证说“案发期间，他看到李某在现场”，这是一份证据材料（E），而命题“案发期间，李某在现场”就是基于证言E的一个证据性事实。区分证据材料和证据性事实是有必要的，因为同一份证据材料从不同的角度可表述为不同的证据性事实命题。有学者提出：就言词类证据来说，一份证言性陈述可以派生出多个命题，甚至陈述者的语气、表情和手势也可以转化为命题，实物证据同样可能需要以多个命题来加以表述，因为实物证据取得的主体、来源、时间、地点、方式以及保管链条都需要转化为命题形式。（[29]，第167 页）

基于证据性事实，推理者可进一步推论出其他假设性事实或解释性事实。根据某些证据或命题，推理者提出假设（假说）以解释这些证据和命题，这些假设所包含的事实，就是所谓的假设性事实或解释性事实，为了方便表达，下文统称为解释性事实。案件事实的认定是以法律适用为导向的，裁判者必须在事实审理过程中完成法律构成要件与案件事实的彼此对应。由此，在案件事实的证明过程中，遵循安德森等人的观点（[2]，第61-62 页），案件事实可以分为不同的层级：最终待证事实、次终待证事实和中间待证事实。最终待证事实是一个案件中存在争议的主要事实命题，即为了给被告人定罪检方需要证明的命题。最终待证事实通常可以分解为多个单独命题，即次终待证事实，它们代表最终待证事实的个体要件，因此也可称为要件事实。证据性事实是一种中间待证事实，中间待证事实本身也是一种解释性事实。实际上，最终待证事实和次终待证事实同样归为解释性事实的范畴，因为它们是对整个案情及其证据进行阐释的事实。

在案件事实的证明过程中，除了从具体案件的证据中获得的知识，还需要运用常识知识。关于世界认知的常识知识可以用概括化命题来表达，一般哲学传统上称为“概括”，在逻辑上被称为“概称陈述（generalization）”。围绕在我们身边的概称陈述很多，例如，“重物总是会往下坠落”“行凶者一般会在作案现场留下痕迹”“神志正常的人通常不会自杀”。这些概称陈述不仅出现在日常生活中，还广泛适用于法律领域。正如舒姆（D.Schum）所言，概称陈述在证据推理中扮演着重要角色。他提出：对于每一个确定的推理阶段或步骤，我们必须对自己所相信的为采取这些步骤提供基础或给予许可的内容做出断言。（[18]，第81 页）此类断言被逻辑学家或法学家称为概称陈述。（[5]）因此，舒姆把概称陈述视为将各种推理组合在一起的“粘合剂”，可以证成证据与待证命题之间的正当性关系。（[18]，第82 页）然而“每枚硬币都有其两面性”，在司法实践中，运用它们又会带来风险，由于概称陈述并不总是普遍为真，往往存在例外。特文宁（W.Twining）主张：概称陈述所表达的一般知识，并非基于证据的知识，而是人类世界的常识知识。这类世界知识存储于知识库中，但人类的知识库却是“一汪纷繁复杂的水，里面含有各种各样的信息、零星记忆、印象、故事、神话、谚语、希望、猜测和偏见等”。（[20]）所以，在证据推理过程中，推理者必须谨慎使用它们，倘若推理者运用主观偏见或者恣意捏造的概称陈述证明案件事实将会带来极大的隐患，这也是刑事错案的主要成因。

综合上面的论述，证据推理可认为是一种基于证据和概称陈述推导出解释性事实主张的常识推理，本质上是一种最佳解释的推论，属于可废止推理。证明过程中的前提可以是证据材料，也可以是解释性事实，而结论是解释性事实，从前提到结论的链接是表达一般知识的概称陈述。为了保障推理的可靠性和安全性，除了审查证据资格外，推理者还必须仔细查验概称陈述的来源、可靠性以及似真性。

3 证据推理的三大方法

3.1 论证方法的最佳解释推论

3.1.1 论证方法的产生与现状

论证的理论渊源追溯到古希腊亚里士多德的三段论。三段论就是一种论证，即由两个直言命题共同推导出结论。发展至今，论证是一个广义的术语，可以用不同的方式进行表述。论证理论家沃尔顿（D.Walton）把“论证”定义为“给出理由来支持或批评有问题或容易引起怀疑的主张”。（[24]，第1 页）这个定义深刻指出了论证的批判性本质，但却过于宽泛，并没有提及支持和主张之间的关系。本文从论辩的视角来解释论证这一术语，将其视为通过运用一系列连续推论步骤，来构建和攻击从证据到结论的“推论树（trees of inference）”。证据推理的论证方法起源于威格摩尔（Wigmore）（[25]）的证据图表法，他开启了一种从证据到假设的可视化研究路径，以图形的方式展现了论证方法。遵循威格摩尔的研究思路，新证据学家安德森、特文宁以理性主义传统为基础，专注于事实推论，形成面向法律人思维的证据推理可视化进路。另一方面，在法律人工智能领域中，通过将逻辑解释为“法学一般化”，形式论辩学家主张（[13,22]），在一个攻击和防卫主张的批判性程序中，逻辑的论辩角色可以用于理性分析论证，形成面向法律人工智能的程序化进路。

3.1.2 案件事实的论证图解模型

论证的基础推理结构可自下而上建模成图1 的形式：根据证据E，推理者按照最佳解释推论的过程构建解释性事实H，概称陈述提供从证据到解释性事实的纽带，使得推理者接受H。基础推理的步骤是建立在这样的概称陈述之上的，即“如果E是H的证据，那么H成立”。由于这类概称陈述反映证据与解释性事实之间的关系，因而可称为证据性概称陈述。（[3]，第27 页）

图1:论证中的基础推理结构

根据证据的数量、证据间的关系和推论出解释性事实的数量，图1 的基础推理结构可细分为四种类型：简单结构、收敛结构、闭合结构、发散结构，如图2。

图2:论证中基础推理结构的四种类型

一个论证往往是由以上四种推理类型链接在一起的树结构，因而可以建模成如图3 的图解形式。在图3 中，最底层是推理的前提，它可以是证据材料或其它假设的命题；箭头表示推理的步骤，由概称陈述提供保证；最顶层的是最终结论，即最终待证事实，它从上到下为各项解释性事实和证据提供解释；其余部分是中间结论，即中间待证事实和次终待证事实。树结构的子树就是这个论证的某个子论证。在实践中运用论证方法时，为了降低论证的复杂性，可以将一个大型论证分解成若干子论证。

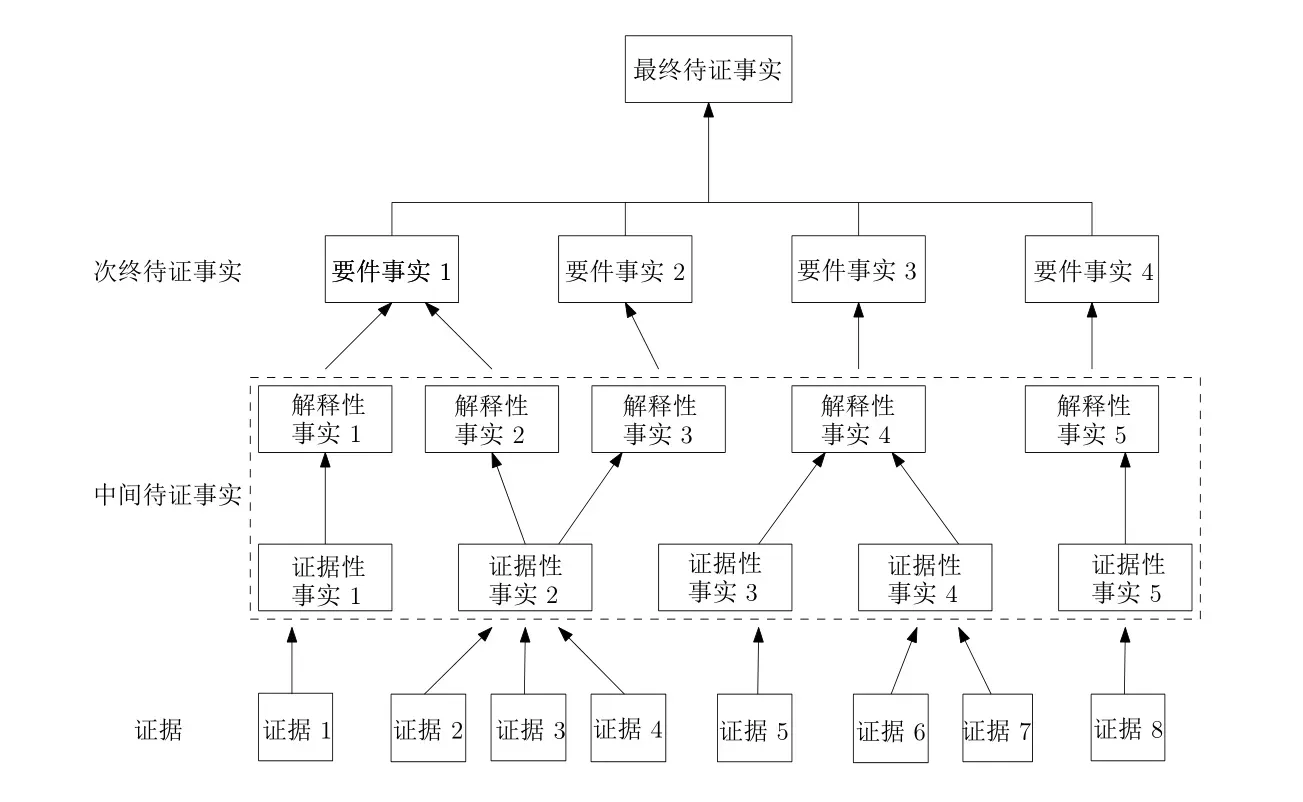
图3:案件事实构建的论证图解模型

按照图3 的图解模型，在分析案件和构建案件事实的过程中，推理者从证据材料、相关假设的命题和概称陈述出发，在最佳解释推论的指导下，逐步向上构建各种解释性事实，形成完整的论证图解。以这种方式来构建整个案件事实，可以实现推理过程的可视化，打破心证黑箱，为理性司法证明提供保障。

3.1.3 基于最佳解释推论的最佳论证

在司法证明过程中，推理者基于最佳解释推论可构造多个论证来解释案件，因此需要比较各种可获得的替代论证，以确定案件的“最佳论证”。比较论证主要涉及最佳解释推论的第二阶段。在论证方法中，各种论证被置于论辩语境中，如果一个论证经受住了攻击、没有被成功质疑，那么这个论证就是可接受的，由此得到的最终待证事实，就是整个案件事实的最佳解释。论证的可接受性可以从攻击博弈和论辩状态两个方面来进行评价。

质疑一个论证有三种途径。（[15]）一是攻击论证的前提，它通过构造另一个论证来说明原论证的某些前提是不可接受的或错误的，这种攻击被称为削弱攻击（undermining attack）。二是攻击论证的推理步骤，即攻击联系前提和结论的概称陈述，它是构建另一个论证来说明原论证为何不能从前提推论出结论的原因，例如概称陈述存在例外的情况，或者概称陈述不具有可接受性等，这种攻击被称为底切攻击（undercutting attack）。三是攻击论证的结论，它通过一个反论证来反驳原论证，反论证的结论与原论证的结论是相互矛盾的，这种攻击被称为反驳攻击（rebutting attack）。攻击论证可以从论证的怀疑源着手。沃尔顿（[23]）为证据推理提供了诸多证明过程中反复使用的论证类型，每种论证类型的怀疑源都通过一组批判性问题而呈现。比如，诉诸从位置到知道论证，相应的概称陈述表述为：如果处于特定领域S位置的证据来源a作证“领域S中的命题A为真（或假）”，那么A为真（或假）。它对应的批判性问题如下：

1.位置问题：a处于知道命题A是否为真（假）的位置吗？

2.诚实问题：a是一个诚实的（可信的、可靠的）证据来源吗？

3.断言问题：a断言A是真（假）的吗？

上面三个批判性问题揭示了诉诸从位置到知道论证的怀疑源，为人们攻击这个论证指明了方向。

论证在经过攻击博弈后所处的状态称为论辩状态。帕肯（H.Prakken）和弗雷斯维克（G.Vreeswijk）区分了论证的三种论辩状态：已证成状态（在与其他论证竞争中获胜）、已推翻状态（在与其他论证竞争中失败）与可防卫状态（在与其他论证竞争中陷入平局）。（[17]）论证的论辩状态取决于它是否击败（defeat）其他论证或被其它论证所击败。底切攻击通常能够击败其它论证，而削弱攻击和反驳攻击能否击败原论证则取决于两个论证的强度的优先关系（preference relation）。刻画论证强度大小的优先关系是一个炙手可热的研究课题。比如，帕肯和萨托尔（G.Sartor）（[16]）建模概称陈述之间的优先关系，阿姆古德（L.Amgoud）和凯罗尔（C.Cayrol）（[1]）建模一个论证框架下整体论证之间的优先关系。然而，到目前为止还没有系统的方法来确定论证强度的优先关系，目前衡量论证强度大小的标准主要都是建立在直觉的基础之上并根据常识知识进行判断。例如，基于甲某的证人证言论证比基于乙某的证人证言论证更加可靠，因为甲某不戴眼镜而乙某戴眼镜，因此前者比后者更为优先。

如果论证A反驳或削弱论证B，那么A击败B当且仅当A优先于B（即A的论证强度大于B的论证强度）。如果两个互相攻击的论证具有相同的论证强度，或者它们的强度的优先关系没有被定义，那么这两个论证就互相击败对方。如果论证A击败B，而论证B没有击败A，则称A严格击败B。然而，即使论证A严格击败了论证B，也不能说明论证A达到了已证成状态，因为A可能会被另一个论证C击败。假定论证B严格击败论证A，而第三个论证C又严格击败论证B本身，这时论证C复原（reinstatement）了A，但同样也不能说明论证C和A达到了已证成状态。因为有可能存在更为复杂的情形，例如又来一个论证D，它和论证C互相攻击对方，接着又来一个论证E，E击败D又复原了C，等等依次类推下去。就论证相互攻击的复杂情形而言，需要一个击败关系之间的演算系统。这个演算系统的输入是一组带有击败关系的论证，输出是对这些论证的三类论辩状态的评价。帕肯的ASPIC+系统提供了一个演算系统的形式框架。（[14]）在这种形式框架中，已证成的论证是那些在与他们的对手的所有冲突中获胜的论证，它击败了所有对手论证，所以可以被接受。已推翻的论证是那些被已证成的论证所击败的论证，因此必须被拒绝。而可防卫的论证是那些涉及到的冲突不能被解决的论证，与其他论证的对抗陷入平局。

由此可见，一个论证如果在与其他替代论证的对抗博弈中已证成，那么这个论证就是“最佳论证”，就可以被接受。因此，已证成的论证就是最佳论证。在论证方法的框架下，对已证成论证的寻找，遵循的正是最佳解释推论的思维过程。

3.2 故事方法的最佳解释推论

3.2.1 故事方法的产生与现状

故事（story）以一种容易为人类处理的方式把信息结构化，在人们理解世界的过程中扮演着重要角色，是人们进行交流的一种普遍形式。亚里士多德是最先讨论故事的人之一，后来一些文学理论和认知心理学家也相继对故事进行了研究。他们的研究兴趣主要在于故事的组成要素、故事的语法结构以及人们如何运用常识知识构建和理解故事。从20 世纪80 年代，一些学者开始转向如何将故事适用于刑事案件中的证据推理，其中,最具代表性和影响深远的当属彭宁顿（N.Pennington）和黑斯蒂（R.Hastie）。他们在班尼特（L.Bennett）和费尔德曼（M.Feldman）研究基础上总结了一套故事方法，即刑事案件的决策过程就是使用该案中的证据构建有关“发生了何事”的故事，然后比较这些故事，从中发现最佳故事。故事方法高度接近于调查人员和法律决策者实际思考案件的方式，因而是自然的，在实践中经常为推理者所运用。故事的因果结构不仅能够帮助决策者记忆证据并判断其重要性，还可以填补案件中没有证据支持的缺口。然而，故事方法存在“好故事排除真故事”的危险，即一个良好结构的、与证据并不充分相容的“好故事”，无论其本身的真实情况如何，会比无结构的、却与证据相容的“坏故事”更加可信。为了降低这个危险，以克劳姆巴格（H.Crombag）为代表的法律心理学家提出了锚定叙事理论（Anchored Narratives Theory），他们主张故事应该锚定于关于周围世界的常识知识之中，锚定于不会受到合理怀疑的安全概称陈述中。锚定叙事理论的锚定过程提供了一种核实故事符合世界知识程度的方法。在此基础上，贝克斯（F.J.Bex）提出了一种混合理论（Hybrid Theory），将论证方法融入故事方法中，以提高故事的可靠性，进一步降低“好故事排除真故事”的危险。

3.2.2 案件事实的故事图解模型

在故事方法的混合理论中，故事是指一个特定的、融贯的、通常按时序排列的状态（state）或事件（event）序列。（[2]）然而，并非任何按时序排列的状态或事件序列都是一个故事，一个状态或事件序列要成为故事，必须满足两个条件：第一，各状态和事件之间不应当包含明显的抵触；第二，状态和事件之间必须要有某种明示的或默示的因果关系。故事中的事件经由因果关系和时间关系之组合相联系，各状态和事件之间的因果关系可以表达为条件陈述，这些条件陈述本质上是一个概称陈述，在故事理论中被称为因果性概称陈述（causal generalization），它具有“H1是H2的原因”之形式。（[3]，第60-61 页）

混合理论中的故事图解模型包含两层结构：故事层和论证层，如图4。一个案件发生后，事实发现者收集相关证据材料，结合常识知识和经验，运用最佳解释推论得出一系列解释性事实，这些解释性事构成了故事中的状态或事件，它们按照一定的时序排序形成一个故事。这个故事就是图解模型4 中的故事层。故事可以用来解释已收集到的证据，也可以预测将来可能会出现的新证据。故事层中的状态或事件要么是以前一个状态或事件为基础，要么是以证据材料为基础，运用最佳解释推论而构建的。状态或事件之间、状态或事件与证据材料之间都存在某种因果联系，它们之间的推理关系都是用因果性概称陈述来提供纽带。从证据材料出发，基于证据性概称陈述，运用最佳解释推论还可以推导出其它解释性事实。这些解释性事实和证据材料形成的树图结构，就是故事图解模型中的论证层。论证层为故事层提供支持，故事层为论证层提供解释。

在混合理论中，证据视为故事被锚定的“基础”，证据与故事之间的联系（“锚链”）是证据性论证中的推论。混合理论区分了两种锚：一是内部锚，即代表故事内部之关系的因果性概称陈述，二是外部锚，即论证中以证据为起点的证据性概称陈述，它们并非故事的一部分。（[3]，第240 页）将论证融入故事，使得证据在故事中有了清晰的位置，已证成的论证为故事中的状态或事件提供支持，故事本身也具有了理性良好基础。

图4:案件事实构建的故事图解模型

3.2.3 基于最佳解释推论的最佳故事

在证据推理过程中，运用最佳解释推论，推理者可以构建多个故事以解释案件中“发生了何事”，例如控方故事和辩方故事。因此，需要从所有可能故事中检验、比较，以确定哪个是“最佳故事”，从而达到事实认定的目的。检验和比较故事主要涉及最佳解释推论的第二阶段。在混合理论中，故事的比较是通过关于故事的论证来完成的。评估故事的质量有多个标准，大致可分为两组。第一组标准是关于故事如何符合案件中的具体证据，即审查故事符合证据的程度，而第二组标准是关于故事是否符合普遍的、常识的世界知识，即审查故事本身的融贯性。

审查故事符合证据的程度有三个子标准：证据支持、证据抵触、证据空缺。（[3]，第87-89 页）证据支持是指支持故事中状态、事件或因果性概称陈述的所有证据构成的集合；证据抵触是指与故事中状态、事件或因果性概称陈述相抵触的所有证据构成的集合；证据空缺是指故事中没有获得直接证据支持的所有事件构成的集合。例如，在图4 中，证据支持有6 个证据，即证据2-7，证据空缺有1 个事件，即事件1，它与证据性事实1 虚线连接表明没有证据支持。这三个子标准分别对应着三个批判性问题（[4]）：

1.多少以及哪些可获得的证据材料支持该故事？（证据支持）

2.多少以及哪些可获得的证据材料抵触该故事？（证据抵触）

3.该解释中的多少以及哪些事件未获得证据材料的支持？（证据空缺）通过回答上面三个问题，就可以审查故事的质量，从而为比较故事的优劣提供依据。很显然，证据支持越多，证据抵触和证据空缺越小，故事符合证据的程度就越高。

审查故事本身的融贯性也有三个子标准：一致性、似真性和完备性。（[12]，第528 页）一致性是指故事中各状态和事件之间不包含内部抵触；似真性是指符合关于周围世界的一般知识；完备性是指故事的要素齐全、结构完整，符合“动机-目的-行为-结果”的故意行为故事图式（story scheme），即行为者的某个动机形成特定的目的，目的进而导致行为，行为产生结果。这三个子标准也分别对应着三个批判性问题（[3]，第94 页）：

1.该故事有互相抵触的状态或事件吗？（一致性）

2.该故事中的事件以及表达潜在因果关系的概称陈述，其内在似真程度如何？（似真性）

3.该故事填满了一个似真的故事图式吗？该故事拟合一个似真的故事图式吗？（完备性）

这三个问题，不需要考虑证据，通过一般的常识知识和经验就能做出回答，从而检验故事的融贯性，为比较故事的优劣提供依据。一致性越强，似真性越高，完备性越足，则故事的融贯性越好。

故事符合证据的程度及其融贯性主要是从故事本身的属性来比较故事的优劣。符合度越高，融贯性越强，这样的故事质量就越高，在与其它替代故事的竞争中就会胜出。此外，为了保证事实认定的准确性，达到排除合理怀疑的证明标准，司法人员应尽其所能构建多个关于案件“发生了何事”的可能故事，使得所有可能故事都应参与竞争，两两进行比较。

类似于论证方法，故事最后的论辩状态分为三种：可信的故事（与其他选择故事竞争获胜），不可信的故事（与其他选择故事竞争失败）与可疑的故事（与其他选择故事竞争陷入平局）。可信的故事就是“最佳故事”。如果论辩博弈中没有故事可信，那么就需要基于最佳解释推论补充证据并重新构建故事以找到最佳故事。因此，对最佳故事的寻找，遵循的也是最佳解释推论的思维过程。

3.3 概率方法的最佳解释推论

3.3.1 概率方法的产生与根基

概率方法应用于证据推理起源于20 世纪后半期，如今已成为一个热门话题。法庭科学家经常谈及使用数值概率的DNA 证据，统计学专家受邀就给定案件情况发生某种犯罪的概率进行作证。概率方法是一种帮助决策者进行不确定性推理和数据分析的有效工具。概率推理以贝叶斯主观概率为基础，贝叶斯公式在其中充当重要角色：

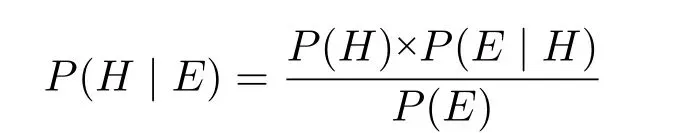
其中P(H |E)为解释性事实H的后验概率，P(E |H)为证据E的似然度，P(H)是H的先验概率，P(E)为证据E的概率。贝叶斯公式也可以写成如下几率（odds）形式：

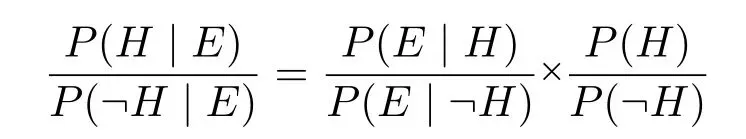
上式等号左边的公式称为解释性事实H的后验几率，等号右边第一个公式称为证据E的似然率（likelihood ratio），第二个公式为H的先验几率。通常，人们运用似然率模型评价证据的证明力（the probative value）（[28]）。与H的先验概率相比较，当似然率大于1 时，证据E将促使H的后验概率增大，而且似然率越大，后验概率将越接近1；当似然率小于1 时，证据E将导致H的后验概率减小，而且似然率越接近于0，后验概率也将越接近于0；当似然率等于1 时，E不提供任何证据价值，后验概率等于其先验概率。

3.3.2 案件事实的贝叶斯网络模型

贝叶斯网络（Bayesian Network，简称BN）是运用概率方法进行证据推理的可视化图解模型。贝叶斯网络是由节点和有方向的弧构成的不带有向圈的图。节点代表随机变量，每个变量关联一个概率分布表。弧代表变量之间的因果关系或概率关系。任何关系的强度都是由概率分布来确定。（[6]）图5 是一个简单的贝叶斯网络，用来分析被告人是否是犯罪现场收集到DNA 的来源。变量可以表示未知的假设，如“被告人是犯罪现场DNA 的来源”，也可以表示被观察的证据，如“现场DNA 被检测为X 型”。每个变量都有明确的取值或状态，这些取值必须是互相排斥且穷尽的。根据变量的取值类型，变量可分为离散变量和连续变量。离散变量的取值是有限的，如布尔变量的取值只有“真”和“假”两种状态，图5 中的变量都是布尔变量。连续变量的取值则是无穷的连续数值。在构建贝叶斯网络时，首先要确定选择何种类型的变量来建模案件中的假设和证据，这里最佳解释推论扮演了关键性作用。推理者根据经验、常识知识和收集到的证据，形成假设，以解释案件和观察到的证据。

当变量选定后，就要考虑变量之间的因果依赖关系、概率依赖关系和时序依赖关系，利用这些关系来确定哪两个变量之间要画弧。弧表示两个变量之间的直接依赖关系，通常弧都是由原因节点指向结果节点，由假设指向证据，由先发生的事件指向后发生的事件。如果两个变量具有直接依赖关系，但不是因果关系，如一个变量表示“人的身高”，另一个变量表示“人的体重”，那么弧的方向通常根据哪个更便于确定条件概率分布表来选择。两个变量之间没有弧，意味着它们不具有直接的依赖关系。贝叶斯网络描绘现实世界的近似模型，在确定节点数量和两个节点之间是否应该画弧时，在现实和效率之间有一个必要的权衡。节点和弧越多，模型的保真度可能会更好，但此时模型的复杂度却很高，从而导致概率计算和信念更新更困难，所以必须在构建更精确的模型和额外建模的成本之间进行权衡。

图5:DNA 来源的贝叶斯网络

3.3.3 基于最佳解释推论的最佳概率

贝叶斯网络包含两个组成部分，一是定性部分，即由案件的证据和解释性事实构成的网络结构图，如图5。这个网络图与论证图解、故事图解一样，都是在最佳解释推论的指导下构建起来的。案件的整体贝叶斯网络由案件要素的子贝叶斯网络图组成，整体贝叶斯网络可以看作是对案件“发生了何事”的一个解释。二是定量部分。定性部分的网络图构建完成之后，推理者就应该按照概率理论给每个变量的取值状态赋予恰当的概率数字，以得到这个变量的概率分布表。在贝叶斯网络中，无父亲结点的变量应赋予无条件概率分布表，有父亲结点的变量应赋予条件概率分布表。概率数字可以是统计意义上的客观概率，也可以是主观概率，客观概率更准确。为使主观概率更可靠，可以采取专家论证形式来综合评价与赋值。

具有定性和定量结构的贝叶斯网络构建完成后，利用概率理论的相关公式，尤其是贝叶斯公式，就可以进行相关的概率推理。贝叶斯网络推理可以实现四个功能。一是计算证据的似然率，从而评价证据的证明力。二是检测怎么样证据组合会产生冲突、出现不一致的情况。三是计算假设的后验概率，实现信念更新。四是寻找证据的最佳解释。对于简单的网络结构，人工就能完成所有的推理计算，但对于较为复杂的网络结构，运用人工智能专家们开发的软件工具可以实现自动计算。在贝叶斯网络中，输入一组证据信息E={E1,E2,...,Em}，然后去计算所有解释变量（非证据变量，表明案件事实的变量）的最可能状态组合，即找到解释变量的某个状态组合{Y1=y1,Y2=y2,...,Yn=yn}，使得P{Y1=y1,Y2=y2,...,Yn=yn |E}最大，这个最大的概率值就是“最佳概率”，它对应的这个状态组合{Y1=y1,Y2=y2,...,Yn=yn}就是证据E的最佳解释。例如在图5 中，如果我们输入证据“现场DNA 被检测为X 型=真”和“被告人DNA 被检测为X 型=真”，那么就能分别计算出解释变量“被告人是DNA 来源”的后验概率，即P{被告人是DNA 来源=真|现场DNA 被检测为X 型=真，被告人DNA 被检测为X 型=真}和P{被告人是DNA 的来源=假|现场DNA 被检测为X 型=真，被告人DNA 被检测为X 型=真}的值。如果前者的数值大，则“被告人是DNA 来源”是上述两个证据的最佳解释。如果后者的数值大，则“被告人不是DNA 来源”是这两个证据的最佳解释。因此，在贝叶斯网络推理中，对最佳概率的计算，遵循的仍是最佳解释推论的思维过程。

4 余论

证据推理旨在构建案件事实，其过程是一种最佳解释推论。论证、故事和概率模型都是评价证据、构建案件事实的理性证明方法。这三种模型有各自评价证据推理的方式，但本质上存在共通之处，即它们都是基于最佳解释推论的方法。在论辩博弈中，已证成的论证，就是最佳论证；可信的故事，就是最佳故事；最大的后验概率，就是最佳概率。最佳解释推论提供的是一种认识论上的接受规则，为关于案件事实做出理性决策提供了指引。最佳解释是对“最佳”案件事实的追寻，契合了司法领域中证明标准的要求。