基于可能性逻辑的结构化论辩理论P-ASPIC+

崔建英

1 绪论

抽象论辩框架（Abstract Argumentation Frames,简记为AF）为表述和评估论证与反论证提供了有效分析工具，是定性化研究不一致信息推理的经典理论。（[9]）近年来，通过对论证进行概率赋值，量化论证中的不确定信息，拓展AF 理论应用，成为人工智能论辩领域中的热点问题，并取得了一系列成果。（[11-13]）概率论辩理论研究中存在概率分布不完全、不一致等问题，文[11,13]提供了用于消解此类问题的合理性概率函数的公设条件，但“概率论中，概率被分配给陈述的真实性或事件的结果，而论证通常既不是陈述也不是事件。那么，赋值在论证上的概率涵义并不清楚；论证上概率所描述的是‘论证为真的真值度’还是‘论证可被相信的信念度’需要被澄清”。（[20]）

可能性理论是关于不确定性的非纯概率理论，其相关的可能性逻辑聚焦可信度层面上的演绎、似真推理和信念修正（[7,8]），更适合不完全信息下知识的表达和推理，因此，基于标准可能性逻辑（Standard Possibilistic Logic）SPL 拓展AF理论可增强其定性和定量分析不确定性推理的能力。不过，由于AF 理论高度抽象，并不能直接用于实践推理。作为AF 理论的一类结构化拓展理论——ASPIC+（[19]），近些年在论证结构方面的研究得到长足发展（[15,16,23])，研究成果可扩展到量化理论的研究中。因而，本文将SPL 逻辑语言作为ASPIC+的底层逻辑语言，重新定义结构化的论证，并利用可能性理论中的NC 规则和SPL 的推导规则，提出了由论证前提、论证中的推导规则及其结论三个维度上的不确定性共同决定的论证强度概念，刻画论证间的击败关系，建构一个拓展的ASPIC+论辩理论——P-ASPIC+。

在P-ASPIC+中，源自可能性理论自身及其逻辑中的推导规则属性，可以简化论证强度的计算，有助快速识别论证间的击败关系，且系统中的论证强度函数完全满足合理论证偏好序的三大性质。（[15,16]）。同时，P-ASPIC+也符合良性论证系统的合理性公设条件。

2 预备知识

2.1 抽象论辩框架AF 和ASPIC+

本节简要回顾论辩框架AF 的主要概念，更详细内容推荐文[9]和[2]。

抽象论辩框架AF 是一组序对AF=(Arg,Att)，其中，Arg是论证集，Att ⊆Arg×Arg是论证间的二元攻击关系。当(A,B)∈Att，则称论证A攻击论证B。如果对于任意的A,B ∈S ⊆Arg，有(A,B)/∈Att，则称论证集S是无冲突的，反之亦然。由论辩框架AF 的几类经典语义，可以获得相应被称为外延的论证集，这些论证集具有内在融贯性（coherent）且可以保护自己免受攻击。

定义2.1(论证的可接受性).给定一个论辩框架AF=(Arg,Att)，对任意论证A ∈Arg，A相对于论证集S是可接受的（acceptable）,当且仅当,对任意攻击A的论证B（B ∈Arg），在S中都存在一个论证C，使得C攻击B，即，∀B ∈Arg:(B,A)∈Att →∃C ∈S:(C,B)∈Att。

定义2.2(论证语义).令S ⊆Arg是一个无冲突的论证集，特征函数F:2Arg →2Arg满足F(S)={A|A相对于S是可接受的}：

·S是可允许的（admissible），当且仅当，S ⊆F(S)；

·S是完全外延（complete extension），当且仅当，S=F(S)；

·S是基地外延（grounded extension），当且仅当，S是极小的完全外延；

·S是优先外延（prefered extension），当且仅当，S是极大的完全外延；

·S是稳定外延（stable extension）,当且仅当,S是攻击所有不在S内的论证的优先外延。

这里，极大或极小是相对于集合包含（set-inclusion）关系而言的。

定义2.3(评估论证).令E ∈{完全语义,优先语义,基底语义,稳定语义}，若在E语义下，论证A被包含在所有E的外延集中（或至少被包含在E的一个外延集），则称论证A是怀疑性合理可证的（skeptically justified）（或称轻信性合理可证的（credulously justified））。

结构化论辩框架理论ASPIC+最初得名于欧盟项目“集成组件论辩服务平台”（Argumentation Service Platform with Integrated Components），并在该项目的研究过程中获得初步发展。文[19]结合文[22]的论证定义及反驳型和底切型攻击的区分，增加前提攻击或称破坏（undermining）攻击，在论辩框架上引入用于确定论证间击败型冲突关系的论证偏好序，并基于AF 抽象论辩框架中的语义评估理论，提出初始ASPIC+框架理论。之后,H.Prakken 和S.Modgil 对已有的成果进行细化和扩展，并验证ASPIC+符合文[3] 所提出的“判定良好论证系统的合理性公设”的条件，使得由该框架系统得出的结论满足合理性假设，确保系统结果在逻辑上的合理性。（[15,16]）因此，相较于提供评估论证语义的AF 理论，ASPIC+关注如何从底层知识库中构造论证，解决了论证内部具体构造、论证间的支持关系的处理以及识别论证间不同冲突关系等问题，进而架起抽象论辩理论AF 与AF 理论实际应用之间的桥梁。因后文中P-ASPIC+较大地保留了ASPIC+中的概念、定义和相关定理的形式化记法，这里不再赘述其形式化定义，推荐参见文[16]。

2.2 标准可能性逻辑SPL

模糊数学创始人L.A.Zadeh 在[24]提出可能性理论，用于刻画不精确和不确定信息：将不确定性理解为可能性，通过依照命题为真的必然性（necessity）和命题为真的可能性（possibility）、以不同的方式对命题进行排序，刻画主体对纯粹序环境中的信念。尽管可能性理论是原始近似推理理论（[24]）的基础，但严格地说，L.A.Zadeh 的方法并没有提供相应的逻辑系统。基于可能性理论，D.Dubois等提出并发展了可能性逻辑（[5]）——一种加权性的完备逻辑系统，以量化方式将信息的不确定性、可信性或优先级与经典逻辑公式联系起来，刻画不确定性信息，对信息的可信性和优先偏好建模推理，是一类用于建模主体信息不完全或部分知识不一致情景下推理的非确定性逻辑。（[6]）标准可能性逻辑SPL（Standard Possibilistic Logic，或称基本可能性逻辑）是本文建构论辩理论的底层逻辑。（关于可能性逻辑的其他扩展逻辑，读者可参看文[6-8]）

具体地，在语法层面上，

定义2.4(标准可能性逻辑公式).标准可能性逻辑SPL 公式是一个二元序对组(φ,α)，其中φ是命题逻辑或一阶逻辑的公式，数值α ∈(0,1]。

这里，公式(φ,α)表示命题φ至少在α程度上是必然或确定的，等价于N(φ)≥α，N是对可能不完全、不确定的信息状态进行建模的必然性度量（可能性理论通过必然性测度及其对偶函数可能性测度Π 两个测度函数联合刻画不确定信息，参见下文定义2.7，详见[5]），α是φ的必然性测度N的下确界。从知识表达角度，它量化了相应命题的可信度（degrees of confidence），即主体关于命题真的信念。本文中，公式(φ,α)表示主体依据其当前信息（或知识）相信命题φ成立的信念度至少为α。另外，N(φ)≥0 总成立，公式(φ,0)不包含任何信息，因此，(φ,0)不是SPL 语言的一部分。

定义2.5(公式集投影).令Γ 是一个有穷SPL 公式集：Γ={(φi,αi)|i=1,2,...,n}，称Γ*={φi |i=1,2,...,n}为集合Γ 的经典投影（classical projection）。

定义2.6(α-截集，严格α-截集).令Γ={(φi,αi)| i=1,2,...,n}，称Γα={(φ,β)∈Γ|β ≥α}和Γα¯={(φ,β)∈Γ|β ＞α}分别为公式集Γ 的α-截集和严格α-截集。

相应地Γα和Γα¯的经典投影分别为

SPL 的公理和推理规则（[5]）：

（经典命题逻辑规则CPL）令φ是经典命题逻辑中的重言式，则(φ,1)1CPL 公理表示命题逻辑的公理，其中，每个公理公式被赋有最大必然度1。；

（必然性弱化规则CW） 若β ≥α，则(φ,β)⊢(φ,α)；

（广义推理规则GMP）(φ,α),(φ →ψ,β)⊢(ψ,min{α,β})。

语义层面上，标准可能性逻辑SPL 中命题公式的可满足性和语义后承等概念是由给定公式集所对应的经典解释集Ω 上的可能性分布π定义（[5]）：

· 可能性分布π满足公式(φ,α)（并将此可能性分布被记为π(φ,α)）：

π |=(φ,α)，当且仅当，Nπ(φ)≥α，其中Nπ表示与π相关的必然性测度;

· 可能性分布π满足公式集Γ={(φi,αi)| i=1,2,...,n}（将此可能性分布记为πΓ）：

π |=Γ，当且仅当，对任意的i ∈{1,2,...,n}，π |=(φi,αi)成立；

· (φ,α)是公式集Γ 的语义后承：

Γ|=(φ,α)，当且仅当，对任意的π，若π |=Γ 则必有π |=(φ,α)。

这里，π是Ω 到区间[0,1]的映射，通过以下约定对事实的实际状态进行灵活的限制，描述主体的知识状态（也称为认知状态）：π(ω)=1 表示ω完全可能成为实际世界，π(ω)=0 表示ω完全不可能成为实际世界；同时，若ω |=φ，则π(φ,α)(ω)=1；若ω |=¬φ，则π(φ,α)(ω)=1-α。直观上表达了阐释公式(φ,α)的基本思想：φ的任何模型都应该是完全可能的，而φ越确定（即α值越大），作为φ的反模型的任何解释则越是不可能。

这样，给定的公式集Γ 将在其解释集Ω 上诱导出一个用可能性分布πΓ进行解码的优先关系:

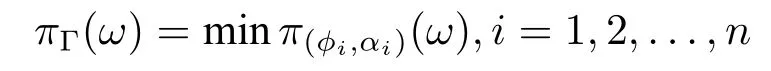
其中，若ω |=φi，则π(φi,αi)(ω)=1，否则π(φi,αi)(ω)=1-αi。

命题2.1.令Γ={(φi,αi)| i ∈Z+}是SPL 公式集，π是Γ 所对应的经典解释集Ω 上任意可能性分布，π |=Γ，当且仅当，π ≤πΓ，即，∀ω ∈Ω,π(ω)≤πΓ(ω)。

考虑到Γ|=(φi,αi) 等价于πΓ|=(φi,αi)，进而等价于∀ω ∈Ω,πΓ(ω)≤π(φi,αi)(ω),i=1,2,...,n，因此，上述命题表明满足语义约束N(φi)≥αi的条件，可能性分布πΓ为每个解释ω分配最大可能性度的分布。

定义2.7(可能性测度和必然性测度).令Γ 是SPL 公式集，φ ∈Γ*，与π相关的可能性测度函数Π 和必然性测度函数N分别为：

其中ω ∈Ω。

定义中，函数Π(φ)用于评估φ在多大程度上与π一致，N(φ)评估φ在多大程度上能够必然地由π所蕴涵。SPL 系统中必然性测度N具有下列规则属性2这里仅列出与本文相关的函数N 的性质，可能性测度函数Π 的性质以及两个函数更多属性，参见文[5,7]。：

· 合取的最小可分解性NC：N(φ ∧ψ)=min(N(φ),N(ψ))；

· 后承关系的单调性NM：若φ|=ψ，则N(φ)≤N(ψ)。

相对于上述的语义解释，文[5]证明了SPL 是完备的：

命题2.2.Γ⊢(φ,α)，当且仅当，Γ|=(φ,α)。

例1.原子命题p,q,r构成的某知识库Γ={(p →q,0.8),(p →r,0.9),(p,0.3),(q,0.7),(r,0.8)}，则Γ 所对应的经典解释集Ω 及其所诱导出的可能性分布πΓ如表1 所示。

表1 :公式集Γ 所对应的经典解释集Ω 及其诱导出的可能性分布πΓ

依上述定义，公式(q,0.3)是公式集Γ 的语义后承，即，Γ|=(q,0.3)（由命题2.2 和(p →q,0.8),(p,0.3)⊢(q,0.3)可得）。当然，由必然性弱化规则CW 及(q,0.7)∈Γ 也可得Γ|=(q,α),∀0≤0.7。但Γ/|=(q,0.8),这是因为：

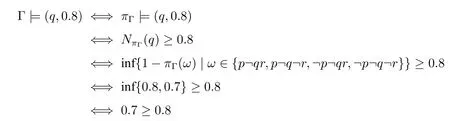
显然不成立。

另，由命题2.1，考虑上例表列中的另一可能性分布π′：∀ω ∈Ω,π′(ω)≤πΓ(ω)，不难验证，π′ |=Γ。例如：π′ |=(p →q,0.8)。这等价于验证即，下式成立：

3 P-ASPIC+论辩框架理论

本节中，我们将联合可能性逻辑和ASPIC+，构建新的结构化论辩理论P-ASPIC+。作为ASPIC+理论的拓展研究，本文尽可能保持与ASPIC+理论中的记法一致。

定义3.1(论辩系统).论辩系统PAS=(L,R,f)是一个三元组，其中：

·L是标准可能性逻辑SPL 语言且满足否定运算（¬）的封闭性3即，若∀Γ ⊆L,φ ∈Γ* 则¬φ ∈Γ*。；

·R={r |r ∈Rs ∪Rd}是推理规则集：Rd表示形如((φ1,α1),...,(φn,αn)⇒(ψ,β),τ)可废止推理规则集；Rs表示形如((φ1,α1),...,(φn,αn)→(ψ,β),1)严格推理规则集,其中,所有的φi,ψ是L*中的元变量4除非特别声明，后文中φ,ψ 等公式均表示取自集合L* 中的元变量。，αi,β,τ ∈(0,1]且Rs ∩Rd=Ø5为保持记法的简洁性，后文中我们通常以(φ1,...,φn ⇒ψ,τ)和(φ1,...,φn →ψ,1)的形式分别表示可废止推理规则和严格推理规则，其中φi,ψ是L*中的元变量，τ∈(0,1)。；

· 规则标名函数f:R →L，且若∀r ∈Rs，则f(r)=(φr,1)；否则f(r)=(φr,α)，α ∈(0,1)。

本文沿用文[16]记法，用ψ=-φ表示ψ=¬φ或者φ=¬ψ。由于本文构建的系统允许攻击发生在可废止推理规则上，也即这类推理规则的有效性可以受到质疑（(¬φr,α)意味着攻击φr相应规则中的推理规则r），因此，推理规则附加上主体的信念度是有意义的，这使得本文中的规则标名函数f(r)∈L是全函数，区别文[16]中规则标名函数。

人工智能领域，通常将被称为知识库的一组良基公式K阐释为智能体相信的一组命题，用以描述主体当前所知道、相信的所有知识（也称信念库）。鉴于本文论辩系统中的推理规则赋有信念度，因此，本文将考察包括推理规则在内的广义知识库。令Γ⊆L，

定义3.2(公式集的一致性，[3]).若(φ,α),(ψ,β)∈Γ，使得∄ψ=¬φ，则称Γ 是一致的；反之亦然。

定义3.3(闭包，[3]).严格推导规则下Γ 的闭包ClS(Γ)是满足下列要求的最小集合：

· Γ⊆ClS(Γ)；

· 如果((φ1,α1),...,(φn,αn)→(ψ,β),1)∈Γ，(φ1,α1),...,(φn,αn)∈ClS(Γ)，那么，(ψ,β)∈ClS(Γ)。

定义3.4(知识库).PAS 系统中的知识库K ⊆L：K=Kn ∪Kp ∪Kr，其中，Kn表示不可驳斥的公理性事实集，且满足其闭包的间接一致性；Kp表示作为普通原子命题的前提集；Kr是被主体赋值不同信念度的规则集。

根据SPL 的公理CPL和定义3.4，命题3.1 表明知识库中公理性知识（即不能被被攻击的事实性的信息）的信念度为1。

命题3.1.若(φ,α)∈Kn，则α=1；

考虑到某些情景中，如主体获取的信息不完全或模糊歧义，主体可能会完全相信一个普通前提，即，∃(φ,α)∈Kp且α ∈(0,1]。因此，命题3.1 的逆命题并不成立；同时，依循文[16]的论证攻击观点，我们要求：论证前提上的攻击仅发生在普通前提上。

至此，一个基于可能性逻辑的论辩理论被定义如下：

定义3.5(论辩理论).论辩理论PAT=(PAS,Π,K)，其中，PAS 是可能性逻辑的论辩系统，K是该系统中的知识库，以及相关知识库K诱导而得的可能性分布函数集Π。

值得注意的是，由可能性逻辑语义，描述知识K的可能性分布πK ∈Π 是满足与K中公式(φi,αi)和形如(φri,βi)这类赋有信念度的推理规则6后文中，为记法的简便性，我们也用形如(di,βi)表示赋有信念度规则的公式。等公式相关的语义约束限制条件：N(φi)≥αi且N(φri)≥βi，且向每个解释分配最大可能性程度的可能性分布。因此，任何满足条件π ≤πK的可能性分布π都与K相一致，使得在论辩理论PAT 中，不存在类似文[11]中概率分布不一致或不完全的问题。

依照文[16]中论证结构化的观点，论辩理论PAT 中的论证概念被修改如下：

定义3.6(论证).给定具有论辩系统(L,R,f)、信念库K及相应的可能性分布π，论证A具有以下几种形式：

(1) (φ,α)，若(φ,α)∈Kn∪Kp且Prem(A)={(φ,α)},Conc(A)={(φ,α)},Sub(A)={(φ,α)},DefRules(A)=Ø,TopRule(A)=undefined；

(2) ((A1,...,An →(ψ,β)),1)，若A1,...,An是论证，使得R中存在关于(ψ,β)的严格推理规则：((Conc(A1),...,Conc(An)→(ψ,β)),1)，其中ψ ∈L* {f(r)}，且，

(3) ((A1,...,An,(ψ,β)),α)，若A1,...,An是论证，使得R中存在关于(ψ,β)的可废止推理规则：((Conc(A1),...,Conc(An)⇒(ψ,β)),α)，其中ψ ∈L*f(r)，且，

注意，条例(2)和(3)中结论的信念度是由GMP和NC规则计算而得（事例见后文）。

沿用[16]关于论证性质的定义，论证可被区分为下列几种类型：

定义3.7(论证类型).若DefRules(A)=Ø，则论证A是严格的（strict）；否则，A是可废止的（defeasible）。若Prem(A)⊆Kn，则论证A是稳固的（firm）；若Prem(A)∩Kp/=Ø，则论证A是可置信的（plausible）。

进一步，若存在关于(φ,α)的严格型论证，该论证的前提取自给定知识库K，则称由库K可推导出(φ,α)，记为K ⊢(φ,α)；若存在关于(φ,α)的可废止型论证，该论证的前提取自给定知识库K，则称由库K可废止地推导出(φ,α)，记为K |～(φ,α)，α ∈(0,β)。

例2.图1 是基于知识库K={(p,1),(d1,0.6),(d2,1)}关于r的论证，其中Kn={p},Kp=Ø,Kr={(d1,0.6),(d2,1)}同时Rs={d2},Rd={d1}:d1:p ⇒q,d2:p,q →r。

该论证是由三个子论证A1,A2,A3构成，其中,A1:(p,1);A2:(p,q,0.6);A3:(p,q →r,1)，且Prem(A2)={p};Sub{A2}={A1,A2};DefRules(A2)={(d1,0.6)};TopRules(A2)={(d1,0.6)};Prem(A3)={p};Sub{A3}={A1,A2,A3};Conc{A2}=(q,0.6)（GMP规则），DefRules(A3)={(d1,0.6)};TopRules(A3)={(d2,1)}。Conc{A3}=(r,0.6)（GMP和NC规则）。

图1:一个关于r 的论证

上述结果表明，基于此知识库K，主体对于“以r为结论的论证A3”为真的信念度不低于0.6。同时，K ⊢(p,1)；K |～(q,0.6)和K |～(r,0.6)。这里，与该知识库相关的一种可能性分布函数πK如表2 所示。

表2:知识库K所对应的经典解释集ΩK及其所诱导出的可能性分布πK

由此可能性分布πK可得，N(r)=inf{1-π(ω)| ω |=¬r}=0.6，与Conc{A3}=(r,0.6)一致。

接下来，为确定论证间冲突关系，我们引入论证强度函数的概念。

定义3.8(论证强度).给定PAT=(PAS,Π,K)，论证强度函数S:Arg →[0,1]满足:

·S(A)=α，若A=(φ,α)∈Kn ∪Kp;

·S(A)=β，若A=((A1,...,An →(ψ,β)),1)且β=min(S(A1),...,S(An))；

·S(A)=β，若A=((A1,...,An ⇒(ψ,β)),α)且β=min(S(A1),...,S(An),α)。

依上述定义，一个论证的强度是由主体对于此论证前提、论证中的推导规则以及论证结论这三个维度上的信念度所决定，这使得论证强度函数S 既保留文[13]中论证强度的涵义,也避免前提的不确定性与论证强度无关的不足，同时满足文[20]的主张——论证强度应由论证前提、论证中所使用的推导规则这些与论证内部本身有关的信息共同确定的。特别地，仅需连续应用GMP和NC规则即可获得给定论证的强度值，且无需考虑“事件独立性”这类在概率环境考虑量化论证强度的限制（[20]）。

本文主张文[16]对于论证间攻击关系的三类细化：底切、破坏和反驳。

定义3.9(论证间的攻击).

· 论证A就B′底切论证B,当且仅当,对于B的某个其顶层规则r是可废止的子论证B′：Conc(A)=-f(r)；

· 对于B的某个形如或形如β)),α)的子论证B′，论证A就B′反驳论证B，当且仅当，Conc(A)=-ψ7考虑到前提的不确定性可以导致论证结论的不确定性，这样，即使论证结论最终是由严格推理规则而得，但含有普通前提的论证依然可以被反驳。因此，本文将反驳关系拓展到包含严格推理规则的论证中。；

· 对于B的某个前提(φ,α)，论证A就φ破坏论证B，当且仅当，Conc(A)=-φ。进而，论证强度可以决定论证间击败关系：

定义3.10(论证间的击败).

· 若论证A就论证B的某子论证B′反驳B且S(A)/＜S(B′)，则A成功反驳B；

· 若论证A就论证B的某个前提(φ,α)破坏B且S(A)/＜α，则A成功破坏B；

· 若论证A就B的某个形如的子论证B′底切B且S(A)/＜β，则A成功底切B；

· 如果论证A成功地或者反驳B，或者破坏B或者底切B，则称A击败B。

考虑到在实际生活中，因某些缘故导致论证A的强度非常小，这使得我们有理由相信A对于B底切可以是无效的，或不成功的。如，有政治企图的经济学者通常不能客观地表达主张（记论证A），那么，这类学者所主张与其政治利益相关的论证（记为B）都将被A底切。然而，如果某学者政治企图的可信性很低，使得A的强度非常小，因此，尽管A依然底切B，但其可能是不成功的底切。因此，与ASPIC+主张“对于底切式的击败仅要求满足A底切B”不同，这里，“A成功底切B”还要满足S(A)/＜β。不过，文[16]所主张“底切是单向攻击”的要求在本文依然成立。

至此，我们可以获得基于可能性逻辑的结构化论辩理论P-ASPIC+：

定义3.11(P-ASPIC+).对应于给定论辩理论PAT=(PAS,Π,K)的结构化论辩理论是满足下列条件的三元组P-ASPIC+=(Ar,C,S)，其中：

·Ar是论辩系统PAS 中，从K构造出满足定义3.6 的最小有穷论证集;

· (A,B)∈C，当且仅当，(A,B)∈Att；

·S是与可能性分布集Π 相关的、定义在论证集Ar上论证强度函数相应地，Dung 式抽象论辩理论定义如下：

定义3.12(P-SAF).对应给定的结构化论辩理论P-ASPIC+=(Ar,C,S)的抽象论辩框架P-SAF=(Ar,D)，其中，D是关于论证集Ar间依照定义3.10 所确定的击败关系。

在SPL 中，GMP和NC都遵循最小化信念度原则，因此，在P-SAF 中，

论证A击败论证B，当且仅当，A攻击B且S(A)/＜S(B)。

前述AF 四种经典语义下评估合理论证的标准同定义2.3 一致，这里不再累述。同时，为了确保P-ASPIC+满足文[15]和文[3]所提出的“合理性论辩理论的公设”（见后文第3 节），P-ASPIC+需要满足转置（transposition）和对置（contraposition）下的封闭性（转置、对置的定义参见文[15]）。

给定某论辩理论，评估最终论证结论的合理可证性（justified）被定义如下：

定义3.13(论证结论的评估).如果φ是一个怀疑性合理可证型论证的结论，那么，φ也是怀疑性合理可证的。如果φ是一个轻信性而非怀疑性合理可证型论证的结论，那么，φ也是轻信性合理可证的。

基于P-ASPIC+，考察下文事例（改变自文[16]例3.7）：

图2:由K 构成的P-ASPIC+框架及其相应的AF 框架，其中论证A、B、C、D分别对应论证A3、B3、C3 和D4

例3.给定知识库K={(p,1),(s,0.7),(u,0.8),(x,0.7),(d1,0.6),(d2,0.7),(d3,0.9),(d4,0.85),(d5,0.8),(s1,1),(s2,1)}，其中d1:p ⇒q;d2:s ⇒t;d3:t ⇒¬d1;d4:u ⇒v;d5:v,x ⇒¬t;s1:p,q →r;s2:v →¬s。由K构成的结构化论辩框架及其相应的抽象论辩框架分别如图2(a)和2(b)所示。

由定义3.6 和定义3.8 知，C1=(u,0.8)且S(C1)=0.8;C2=(C1,(v,0.8),0.85)，且S(C2)=min{S(C1),0.85}=0.8；进而,S(C3)=min{S(C1),S(C2)}=0.8；实际上，也可应用GMP规则：由(u,0.8),(u ⇒v,0.85)⊢(v,0.8)；进而，由(v,0.8),(v →¬s,1)⊢(¬s,0.8)；即，由C3=((C1,C2→(¬s,0.8)),1)，则，S(C3)=0.8；同理可得:S(B3)=0.7。

考虑论证D4：由D4=((D2,D3,(¬t,0.7)),0.8)，其中，D1=C1,D2=C2,D3=(x,0.7)且S(D2)=S(C2)=0.8；S(D3)=0.7，故，S(D4)=min{S(D2),S(D3),0.8}=0.7；同样，应用GMP和NC规则：由(u,0.8),(u ⇒v,0.85)⊢(v,0.8)，那么，由N(v ∧x)=min{N(v),N(x)}=0.7 且(v,0.8),(x,0.7),(v,x ⇒¬t,0.8)⊢(¬t,0.7)，可得，S(D4)=0.7；同理可得S(A3)=0.6。

这样，因为S(C3)=0.8＞S(B3)=0.7;S(D4)=0.7=S(B3)=0.7;S(B3)=0.7＞S(A3)=0.6，则由定义3.10 知，论证C3成功破坏了论证B3，即C3击败B3；论证D4和B2彼此成功反驳了对方，即D4和B3相互击败；而B3击败了A3,因为B3成功底切了A3。

对应到P-SAF理论中，在前述四种经典语义下，都存在唯一相同的外延E=={A1,A2,A3,C1,C2,C3,D3,D4}，并且结论r既是怀疑型也是轻信性合理可证的。

4 论证偏好与论证强度

文[15]、[3]讨论了合理的论证偏好序应当满足的三个性质：(1)论证强度完全由可废止规则和前提决定；(2)严格且牢固的论证好于其他论证；(3)偏好序的无环性且满足：若论证A好于论证B，则A也好于B的某个极大非可靠（maximal fallible）（即，可废止的或可置信的）子论证B′。8某论证B 的子论证B′ 是极大非可靠的：(1)若B′ 的顶层导规则是可废止的或是普通前提；(2)不存在B 的其他子论证B′′，使得B ∈Sub(B′′)且满足条件(1)。

在P-ASPIC+中，我们通过论证强度刻画论证间偏好关系（A ≤B等价于S(A)≤S(B)），进而确定论证间击败关系，因此，强度函数S满足性质(1)。下文定理4.1 则分别确保S也满足后两个性质要求。

定理4.1.给定结构化论辩理论P-ASPIC+=(Ar,C,S)，强度函数S满足：

(1) 若Prem(A)⊆Kn且DefRules(A)=Ø（即A是牢固且严格的论证），则S(A)≥S(B)，∀B ∈Ar且Prem(B)/⊆Kn或DefRules(B)/=Ø；

(2) 集合{S(A)|∀A ∈Ar}是有界全序集；

(3) 设A,B ∈Ar，且B′是B中极大非可靠子论证，那么，若S(A)＞S(B)，则S(A)＞S(B′)。

证明.

· 若Prem(A)⊆Kn且DefRules(A)=Ø，则根据论证强度定义2.1，S(A)=1。进而，S(A)≥S(B),∀B ∈Ar且Prem(B)/⊆Kn或DefRules(B)/=Ø；

· 由定义3.8，易得：0≤S(A)≤1，且{S(A)|∀A ∈Ar}中≤具有反对称性、传递性和三歧性。

·（反证）若不然，则对于B中任意一个极大非可靠子论证B′，都有S(A)≤S(B′)，

-若B′=B，则S(A)≤S(B)，与已知条件S(A)＞S(B)矛盾；

-若B′/=B，由于B′是B中任意一个极大非可靠子论证，那么，根据GMP和NC规则，若S(A)≤S(B′)，则必有S(A)≤S(B)，同样与已知S(A)＞S(B)矛盾。

故,假设不成立，定理得证。

5 合理性公设的讨论

文[3]提供判别基于规则论辩系统优劣的合理性公设，实例表明一个好的论辩系统应当满足这些性质的必要性。本节中，我们将证明相对于基底语义，P-ASPIC+符合这些合理公设要求。

合理论论辩系统的公设（[3]）令E是给定语义下的任一外延，

子论证的闭包性∀A ∈E，若A′ ∈Sub(A)，则A′ ∈E；

严格规则的闭包性{Conc(A)|A ∈E}=ClS(Conc(A)|A ∈E)；

直接一致性{Conc(A)|A ∈E}是一致的；

间接一致性ClS({Conc(A)|A ∈E})是一致的；

P-ASPIC+并无改变ASPIC+中的子论证定义，则由文[19]中命题6.1 和命题6.2 知：

定理5.1.给定某结构化论辩P-ASPIC+=(Ar,C,S)理论，E是基底语义下的外延，那么，对于任意论证A ∈E，若A′ ∈Sub(A)，则A′ ∈E。

具有对置或转置下的封闭性确保P-ASPIC+满足严格规则的闭包性：

定理5.2.给定某结构化论辩理论P-ASPIC+=(Ar,C,S)，E是基底语义下的外延，那么，对于任意论证A ∈E，{Conc(A)|A ∈E}=ClS({Conc(A)|A ∈E})。

证明.（反证）假设P-ASPIC+不具备严格规则的闭包性，这等价于：∃(φ,α)∈{Conc(A)|A ∈E}，且((φ,α)→(ψ,β),1)∈Rs但(ψ,β)/∈{Conc(A)|A ∈E}，那么，因为((φ,α)→(ψ,β),1)∈Rs，则由GMP知，β=α，即，

因为主张结论φ的某论证Ai ∈E且主张结论ψ的某论证Bi/∈E，则，对于主张结论¬φ的论证和主张结论¬ψ的论证其中这等价于,

由((¬ψ,β′)→(¬φ,α′),1)∈Rs（P-ASPIC+转置封闭性）推知，α′=β′，即，N(¬ψ)=N(¬φ)。那么，由(2)式，N(φ)＞N(¬φ)=N(¬ψ)＞N(ψ)；这与(1)式矛盾，故，原假设不成立，定理得证。

文[15]证明：当基于ASPIC+框架的论辩理论是良定义（well-defined）的（即，该理论满足公理事实的一致性，且具有推导规则的转置和对置的封闭性，以及关于论证间的偏好序是合理的），则这类ASPIC+论证也满足上述2 个关于一致性的公设要求。因此，依据定理4.1、定义3.4 及具有转置和对置下的封闭性的P-ASPIC+，我们可得：

定理5.3.给定结构化论辩理论P-ASPIC+=(Ar,C,S)，E是基底语义下的外延，那么，{Conc(A)|A ∈E}和ClS({Conc(A)|A ∈E})都是一致的。

6 相关研究比较

文[4]和文[1]都是联合可能性逻辑和形式论辩理论的研究。文[4]将必然性值添加到推导规则中，依据GMP规则，通过论证传递生成这些推导规则的最大推演度——推导规则强度，将其用于区分细化论证间的攻击和击败关系。文[4]定义论证间击败关系的技术做法与本文相似。但由于[4]旨在拓展可废止逻辑程序设计（DeLP）——一类基于规则的论辩理论，使得论证中的可废止性被限定在推导规则间;本文是关于AF 理论（或结构化论辩理论ASPIC+）的拓展研究，论证前提或推导规则都可能存在可废止性。文[1]综合基于论辩的谈判方法和寻求权衡（trade-off）的启发式方法的优势，构建了一类基于可能性逻辑的协商谈判框架，用于提出一种新的谈判方法。无论是在研究对象和研究目标上，文[1]不同与本文工作。

在可能性理论的量化应用研究中，必然性测度和可能性测度分别对应概率测度的上、下确界，因此，有必要将本文的工作与近年来发展起来的概率论辩理论进行比较研究。特别是由A.Hunter，M.Thimm 等学者在概率论辩理论研究方面所做出开拓性的工作。（[10-14,17,18,21]）

取决于不确定性是否存在论证之中或是围绕着论证，当前概率论辩理论的研究可分为两种：概率被用于表达“主体是否接受某个论证在论辩框架中应当存在的不确定性”，也即“存在于论辩图拓扑中的不确定性”（[13]），这是概率在论证中的外部使用（[11]所称的集群式（constellations）方法）；利用概率描述主体对于论证其前提的真实性或其推论可靠性的研究属于概率在论证中的内部使用（[11]所称认知论（epistemic）方法）。类比下，本文可归属到可能性论证的“认知论方法”的研究。同文[11,13,18]等一系列关于概率认知式论证研究相比，尽管两类研究具有相同的核心思想——量化论证的信念度，和相同的研究目标——拓展抽象论辩理论，但由于本文所基于的底层理论是可能性理论及其逻辑系统SPL，研究对象是结构化论辩框架ASPIC+，使得两类研究在技术方法和结果呈现上存在明显的差别：前者通过语言模型上的概率分布捕捉论证的不确定性，经典逻辑论证的强度被定义为所有前提合取的概率或将论证强度定义为给定前提下论证结论的条件概率（[13]）；本文讨论结构化论辩，论证的不确定性由满足语言模型上的可能性分布、论证前提和推导规则共同刻画，论证强度由论证前提、论证中所使用的推导规则这些与论证内部本身有关的信息共同确定的。特别地，可能性分布的非可加性不确定性模型使得P-ASPIC+中的可能性分布不会出现前者理论中所存在的“概率分布不完全、不一致的问题，因此，为避免出现不完全和不一致的概率分布，文[11,13]所讨论的合理概率函数的若干公设在本文中并不需要考虑。

7 结语

基于可能性逻辑，本文建构一个符合良好论证系统公设条件的结构化论辩理论P-ASPIC+,实例展示其对不确定性知识的量化处理，扩展原有结构化论辩理论ASPIC+定性化推理能力。特别地，P-ASPIC+中论证强度概念能够自然清晰阐释论证中的不确定性，且论证强度函数S 使得我们仅通过数值比较即可确定论证间的偏好关系，识别论证间的击败关系。条件化P-ASPIC+可废止性推理规则的信念度，使其满足文[19]中最后链和最弱链规则相应的适用原则（用于论证偏好序的确定）是未来研究关注的重点。同时，考虑到可能性逻辑可通过公式截集所诱导的分层结构处理知识库的不一致性（[6]），和基于可能性逻辑的图氏贝叶斯类网络的应用开发（[8]），因此，联合这些技术成果到论辩聚合和贝叶斯网络的论证分析中，也是未来进一步的研究方向。