电子稳定平台在无人船干扰设备上的应用
2022-03-31力沈佳琪戴
姚 力沈佳琪戴 欢
(中国船舶集团有限公司第八研究院,江苏 扬州 225101)
0 引言
无人艇出现较晚但发展迅速,相比其他移动式观测平台,无人值守的特性决定了其具有良好的环境适应性和经济性。它行动灵活快速,在危险海域、恶劣环境下具有无可比拟的巨大优势。无人船也存在一定劣势,体积小,灵活的同时受海情水况影响更剧烈,对船载设备的体积、质量、精度以及灵活性、反应速度要求更高。电子稳定平台省去了机械结构,通过姿态传感器实时测量船体纵、横摇等姿态信息,并进行坐标变换,直接补偿给方位及俯仰控制器,实现精确跟踪。
1 干扰指向设备伺服控制基本原理
侦察设备发现目标,并将目标信息(方位、俯仰)送给干扰设备;干扰设备根据侦察设备的位置信息对目标信息进行解算,得到目标点相对于自身的方位、俯仰信息,并结合船身的纵横摇进行补偿;最后控制执行机构进行动作,实现对目标的跟踪及干扰。如图1所示,、分别为侦察设备、干扰设备位置,为目标点,以、为原点分别建立、坐标系,、分别为(目标点)在2个坐标系上的投影,、、、分别为目标点对应2个坐标系的俯仰、方位角。
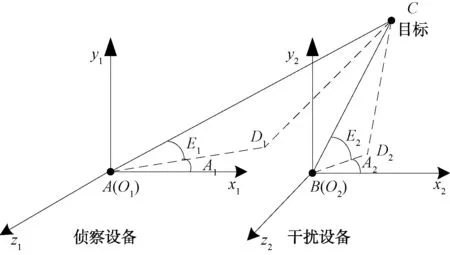
图1 侦察设备目标解算
为大地直角坐标系,指向直角坐标系,沿铅垂线向上,按右手定则确定。
2 纵横摇补偿坐标变换[5-6]
2.1 极坐标与直角坐标转换
如图2 所示,将点的直角坐标转换为极坐标:

图2 直角坐标与极坐标

式中:为目标点距坐标原点的距离;为俯仰角;为方位角。
2.2 纵横摇补偿[7]
(1) 横摇角影响
仅横摇角影响时,认为是绕轴旋转,轴方向分量不变,和轴转角度。设变化前直角坐标为(,,),变化后为(,,),可得:

(2) 纵摇角影响
仅纵摇角变化时,可看做绕轴旋转,轴方向分量不变,和轴转角度。设变化前直角坐标为(,,),变化后为(,,),可得:

(3) 航向角影响
仅航向角变化时,可看做绕轴旋转,轴方向分量不变,和轴转角度。设变化前直角坐标为(,,),变化后为(,,),可得:
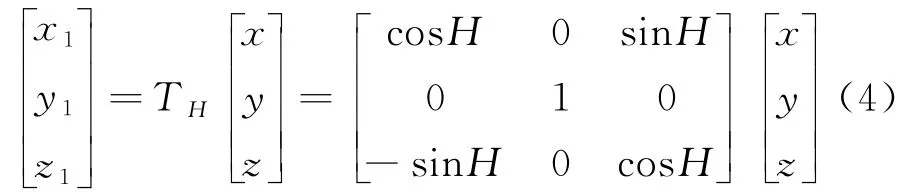
(4) 纵横摇以及航向的影响为:
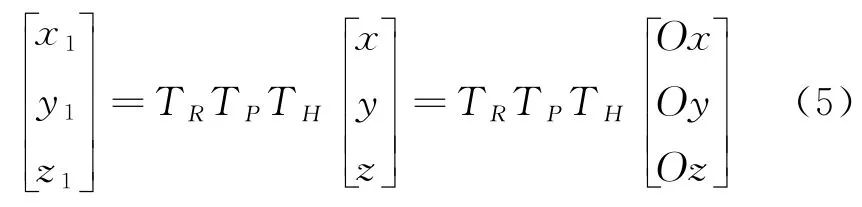

式中:(,,)为极坐标系下的目标位置。
将式(1)、(2)、(3)、(4)代入式(5)可得:
为计算方便,进行归一化处理,将距离参数舍去。
(5) 航向及纵横摇补偿后的俯仰、方位计算:

3 MATLAB仿真验证与DSP实现
3.1 仿真与验证
基于MATLAB/Simulink编写m 语言程序对坐标变换公式进行仿真验证。图3和图4分别为仿真模型和纵横摇角度变化对方位俯仰角度变化影响的仿真结果。

图3 电子稳定平台MATLAB/Simulink仿真

图4 方位、俯仰的纵横摇补偿
利用MATLAB/Embeded Coder Toolbox,将MATLAB文件进行编译,直接下载到DSP28335进行测试。方位角、俯仰角、航向角保持不变,改变纵横摇角度,对方位、俯仰角度进行补偿计算,部分结果如表1所示。

表1 纵横摇补偿运算结果
表1对计算结果采用小数点后3位,方位、俯仰补偿的数字信号处理(DSP)计算误差均小于0.001,可以满足后续伺服控制系统的精度要求。
3.2 试验结果及分析
无人船载设备抛锚在一固定点位,给定一连续的虚拟目标航迹,干扰设备伺服机构动作,指向目标位置,实现干扰设备对目标的跟踪和实时干扰,部分实验数据见表2~表5。由实验及计算结果可知,跟踪误差小于2°,满足设计精度要求。图5、图6分别为设备指向的方位俯仰实际角度以及与目标角度的误差。

表2 设备位置GPS信息

表3 目标位置GPS信息

表4 无人船载设备姿态数据

表5 方位数据及误差

表6 俯仰数据及误差

图5 方位角度及误差
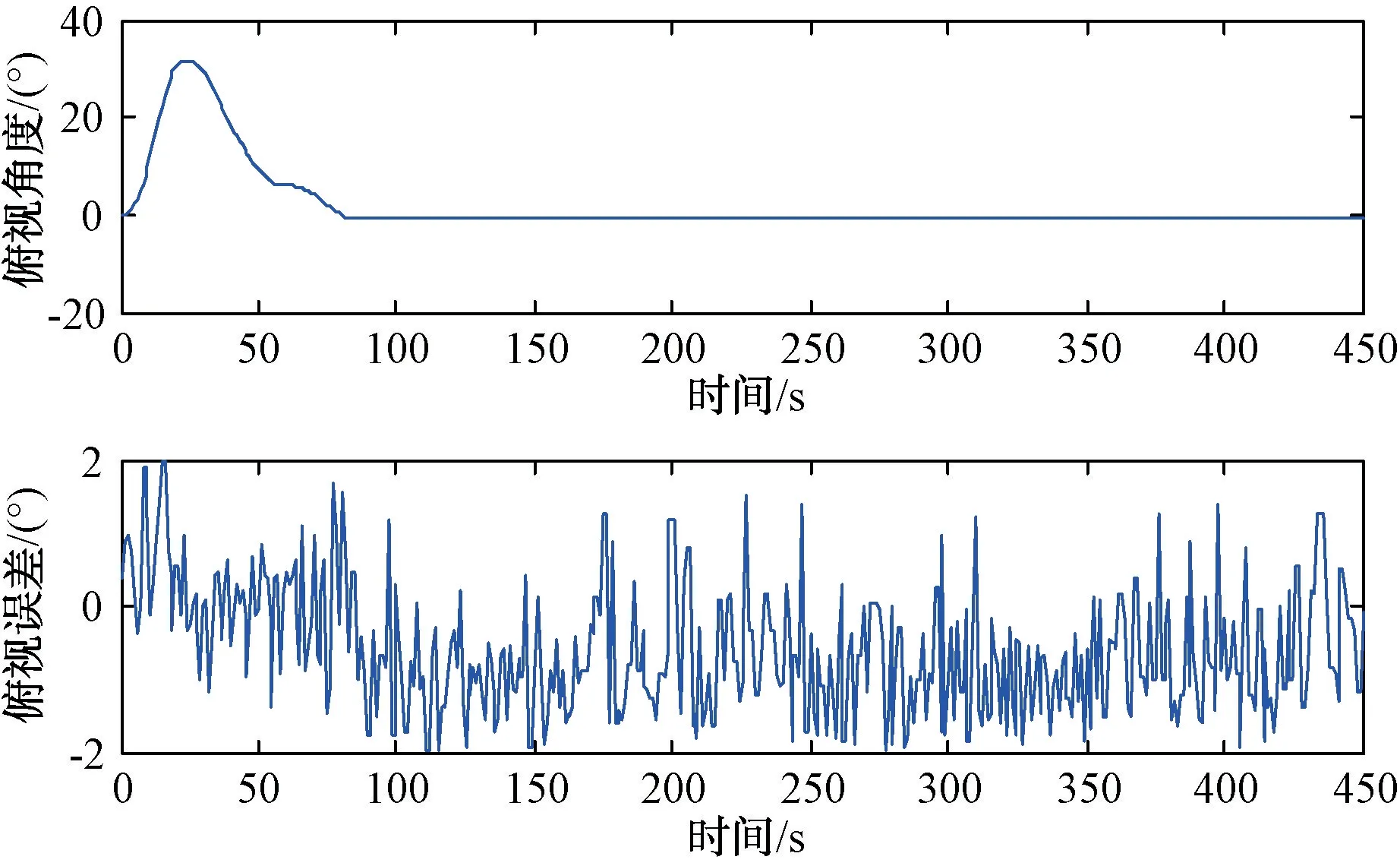
图6 俯仰角度及误差
4 结束语
本论文论述了一种基于无人船干扰设备的电子稳定平台的实现方法,仿真测试及试验结果显示,该方法可以有效地实现船体纵横摇及航向变化对干扰设备方位俯仰的干扰补偿,在实际应用中效果良好,有效补偿了船体纵横摇对无人船载设备的影响。
