GM(1,1)残差处理模型的变形预测实践与分析★
2022-03-30常国霞
翟 敏,常国霞
(中国建筑材料工业地质勘查中心山西总队,山西 太原 030031)
1 概述
建筑工程项目在施工建设阶段的变形监测是保障工程安全顺利进行的必要手段,是安全措施决策分析的必要依据,其往往延续至项目运营阶段[1]。在观测得到变形数据后的数据分析阶段中,变形预测是其中的一项重要内容;它是依据现有数据以及相关资料,对后期未发生的或可能发生的变形进行预测。经过实践以及科学研究,目前变形预测的方法已经有很多种。而灰色系统理论中的GM(1,1)模型具有小样本、贫信息建模的特点[2-3],变形数据具有灰色数据特征,因此其在变形预测领域的应用已经得到较大推广。其中王凯伦等[4]采用灰色GM(1,1)模型,根据山东某矿区地表移动观测站实测资料,对开采沉陷预测精度进行了分析研究;邱利军等[5-6]采用改进的GM(1,1)模型对基坑沉降数据以及大坝变形数据进行了预测分析研究;丁万涛等[7]、王新胜等[8]则针对隧道围岩变形,采用灰色模型进行了分析研究;姚颖康等[9]针对滑坡变形采用改进GM(1,1)模型进行预测,取得比传统模型好的效果。本文采用实际工程项目中某建筑物主体沉降监测数据为分析依据,建立均值GM(1,1)模型、残差GM(1,1)模型以及坐标变换模型进行变形预测,并对预测结果进行了对比分析,得到坐标变换模型预测效果较好的结论。认为对相似工程的模型选取及实践具有一定参考价值。
2 均值GM(1,1)模型原理及残差处理
2.1 均值GM(1,1)模型
设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),其中,x(0)(k)≥0,k=1,2,…,n;X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),X(1)为X(0)的1-AGO序列,计算公式为:
(1)
其中,k=1,2,…,n。
设Z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),其中:

(2)
x(0)(k)+az(1)(k)=b
(3)
称式(3)为均值GM(1,1)模型。
(4)
其中:
(5)
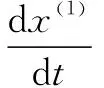
(6)
称式(6)为均值GM(1,1)模型的白化微分方程,也称影子方程。
均值GM(1,1)模型的时间响应函数为:
(7)
若k≤n为模拟,若k>n为预测。累减还原式为:
(8)
而对应的X(0)的时间响应函数是:
(9)
2.2 残差GM(1,1)模型
残差GM(1,1)模型是以GM(1,1)模型的残差序列再次建立GM(1,1)模型以进行修正的方法。
设ε(0)=(ε(0)(1),ε(0)(2),…,ε(0)(n)),其中:
(10)
式(10)为X(1)的残差序列。
若存在ki使得:
1)∀k≥ki时,残差序列符号一致。
2)n-ki≥4。
则包含ε(0)(ki)及其之后序列的序列段可用于建模。
当k≤n时,是对拟合序列的修正;反之,则是对预测序列的修正。需要注意,若残差序列不满足符号一致的要求,可采用文献[5]中的加常数的方法进行序列变换后,建模预测,最后将预测结果反向还原即可。
2.3 坐标变换修正残差
文献[6]认为,GM(1,1)模型在拟合段末期,拟合一次累加数据与实测数据的一次累加值出现相近、相交或相离的趋势,致使后期预测数据出现偏差;因此,提出采用坐标变换的方法,修正预测值以减弱残差影响。
首先以建模序列的一次累加序列最末项与一次累加序列的拟合值最末项计算平移量:
(11)
其目的是使得纵向平移后的一次累加序列已知值与拟合值在最末项重合。然后得到平移后的时间响应函数为:
(12)
然后计算旋转角度,为:

(13)
即以一次累加序列的拟合值与已知值的最后两项构成的直线计算夹角作为旋转角。
在计算完旋转角度后,即可利用下式对预测数据序列进行旋转变换:
(14)
其中,(x0,y0)为对应建模序列最末项对应的一次累加序列已知值;(x,y)为对应一次累加序列预测值的横纵数值;(x′,y′)为对应变换后的横纵数值。
最后,在变换后点序列相邻点构成直线或直线延长线上计算对应横向数值的纵向值作为一次累加序列的预测值。公式为:
(15)
3 工程实例应用及比较分析
选用某建筑物主体沉降观测2号点实测9期数据为依据,采用前7期数据建立均值GM(1,1)模型,然后以残差模型和坐标变换两种改进形式对残差进行处理,以后2期数据进行验证。其实测数据如表1所示。

表1 实测变形数据序列
采用C#语言编程对均值GM(1,1)模型以及两种改进进行实现后,建模预测,得到后2期数据的预测结果如表2所示,预测结果的相对误差如表3所示。

表2 不同模型预测结果 mm

表3 不同模型预测值的相对误差 %
通过分析表2与表3可知,均值GM(1,1)模型预测精度较低,而残差GM(1,1)模型相较于均值GM(1,1)模型的预测精度有所提高,而坐标变换改进模型的预测精度最高。从实例看,在第8期,坐标变换模型预测值几乎与实测值重合(其中涉及小数点后位数取舍),而第9期数据预测值相对误差为-3.98%,绝对误差为-0.68 mm。而均值GM(1,1)模型以及残差GM(1,1)模型的预测精度是不能接受的。需要说明,在残差序列建模过程中,由于残差序列不满足建模要求,采用了残差序列加常数1后的序列进行建模,且采用的是加常数后满足要求的第2期至第7期数据,对预测结果进行反向还原得到修正值。
预测期的预测数据与实测数据比较如图1所示。

从图1可知,残差模型和坐标变换模型均是将预测值向实测的校正,但校正值的大小决定因素不同。前者取决于GM(1,1)模型的预测值,而后者取决于模型的平移量和旋转角。从图1也可以发现,一次累加的旋转在累计沉降的预测值中有所体现。且在图上可以看出,坐标变换模型相较于均值GM(1,1)模型以及残差模型,预测精度优势明显。
4 结语
在建筑工程施工阶段,变形监测是保障工程安全进行的必要手段。本文以沉降变形监测实测沉降数据序列为基础,选取监测点9期实测沉降数据进行预测实践应用分析,选择前7期建立不同模型,后2期进行对比验证,在程序实现相关模型的基础上对预测结果进行对比分析,认为坐标变换模型的预测结果达到了较好的预测效果,与实测累计沉降量相 近,其可以作为相似工程的预测选用方法,对相关实践工作具有一定参考价值。
