大直径复合绝缘子法兰节点抗震性能及设计参数影响研究

曹枚根，张若愚，黄清，邸悦伦

(1.北方工业大学 土木工程学院，北京 100144；2.上海大学 力学与工程科学学院，上海 200444；3.江苏神马电力股份有限公司，江苏 南通 226599；4.电网输变电设备防灾减灾国家重点实验室(国网湖南省电力公司防灾减灾中心)，湖南 长沙 410129)

特高压电网迅速发展，对于变电站及输电线路的绝缘子机械性能有了更高的要求[1-3]。大多数设备都由支柱绝缘子支撑，随着电压等级的提升，设备高度不断升高，在地震作用下会由于结构承载能力不足导致电气设备的损伤，严重时可能导致大面积输变电工程停电[4-7]。玻璃纤维增强树脂复合材料绝缘子(以下简称复合绝缘子)具有质量轻、力学性能优异及抗震能力好等特点，逐渐取代传统陶瓷绝缘子成为超、特高压电气设备外绝缘的主流选择。目前我国已能自主研发、设计及生产制造300 mm以上复合绝缘子，并在中、重污区和地震区得到了广泛应用[8]。除材料密度、强度、弹性模量等基本物理力学属性外，瓷质绝缘子和复合绝缘子最大的区别在于套管与法兰连接段的胶装工艺。瓷绝缘子法兰节点由胶装水泥将瓷套与法兰连接，胶装水泥厚度大，可作为受力结构；复合绝缘子法兰节点由轻质粘结剂将复合套管与法兰连接，胶装厚度仅为1 mm左右。这也直接导致2种绝缘子法兰节点受力状态不同。研究表明[9-11]，复合电气设备主要破坏型式为法兰节点在弯曲荷载作用下发生的粘结滑移破坏，即套管与法兰脱粘，但复合套管本身基本没有破坏。因此，在复合支柱绝缘子的众多力学性能中，法兰胶装节点在弯曲荷载下的承载力及刚度是最关键的力学指标之一。

超、特高压支柱类电气设备通常安装在支架上，高度大、重心高，设备根部承受弯矩大，在地震作用下法兰节点容易发生粘结破坏，有必要研究复合绝缘子的法兰节点的抗震性能和低周往复荷载作用下的损伤机理[12-21]。吴光亚等[12]建立了1 100 kV复合支柱绝缘子有限元模型，通过改变法兰壁厚、加劲筋及胶装比等参数开展仿真计算，分析结构参数对绝缘子机械强度的影响；马艳枝等[13]采用内聚力裂缝材料模型模拟瓷绝缘子在受弯矩外载下界面脱粘失效的过程；李圣等[14]通过对复合支柱绝缘子开展静力侧推试验，发现复合支柱绝缘子中套管与金属法兰的胶装连接段刚度明显小于套管刚度；张玥等[15]对2只不同高度的特高压复合支柱绝缘子开展静力侧推试验和破坏前后的动力特性试验，发现粘结破坏时绝缘子的基频下降明显；曹枚根[16]等通过对3支瓷质绝缘子进行振动疲劳试验，得到了绝缘子振动频率与加载次数之间的关系，反映了绝缘子节点刚度的下降情况；石忠强等[17]建立220 kV SF6断路器瓷套有限元模型，计算胶装比、胶装厚度、胶装外径和法兰内表面齿形结构对瓷套受力的影响。目前，在对支柱类复合材料电气设备进行力学分析时，将法兰节点段与套管连接视为刚性或半刚性[22-24]，国内外的抗震设计规范将法兰与绝缘子的连接节点简化为梁单元进行计算，梁单元的等效刚度是线性的。支柱类绝缘子为长悬臂结构，法兰根部受到的弯矩较大，但若法兰节点未发生破坏，法兰节点受拉压两侧胶体应力分布均匀；复合绝缘子法兰节点破坏时往往伴随着胶体的逐渐开裂和受拉侧连接界面滑移，从上到下的胶体开裂会导致复合绝缘子整体的非线性，此时线性段刚度无法反映法兰胶装节点开始破坏至完全破坏的非线性过程。图1为复合绝缘子法兰胶装节点发生破坏前后胶体受力变化。

图1 法兰胶装节点在弯矩荷载下破坏前后的受力特点Fig.1 Mechanical characteristic of flange gluing joint before and after failure under bending moment load

目前关于复合绝缘子法兰节点非线性力学性能的研究较少，大部分研究还是以瓷绝缘子为主，导致复合绝缘子的动力时程分析计算结果误差较大。为此，在进行复合绝缘子在地震作用下的动力时程分析前，应先得到在低周期往复荷载作用下法兰胶装节点的受力性能，用来反映抗震性能的同时，也能体现节点的非线性力学行为。

为此，本文建立大直径复合绝缘子法兰节点精细化有限元模型，通过控制位移的手段施加低周期往复荷载开展抗震性能模拟计算，分别得到套管整体结构和法兰胶装节点的滞回曲线，通过内聚力材料模型模拟法兰节点粘结剂在静力荷载作用下脱粘破坏过程；随后改变法兰壁高度、套管壁厚及粘结剂强度等3个法兰关键设计参数，通过比较不同参数下的滞回曲线、骨架曲线及等效粘滞阻尼比，分析3个设计参数对复合绝缘子抗震性能的影响。研究分析典型复合绝缘子法兰胶装节点抗震性能及其主要影响参数，可为复合绝缘子非线性本构及非线性抗震计算提供理论支撑。

1 复合绝缘子有限元模型

1.1 复合绝缘子主要力学参数

本文以单节±800 kV复合支柱绝缘子为研究对象，其主要由空心套管和金属法兰组成，套管外径为320 mm，为典型的复合绝缘子结构。套管材料为玻璃纤维增强树脂复合材料(以下简称为复合材料)，法兰材料为高强铝合金，表1为材料主要力学参数。伞裙的质量均匀分布在复合套管上，表1中复合材料的密度为考虑橡胶伞裙的综合密度，但伞裙刚度较小，在计算时不考虑伞裙的弹性模量。

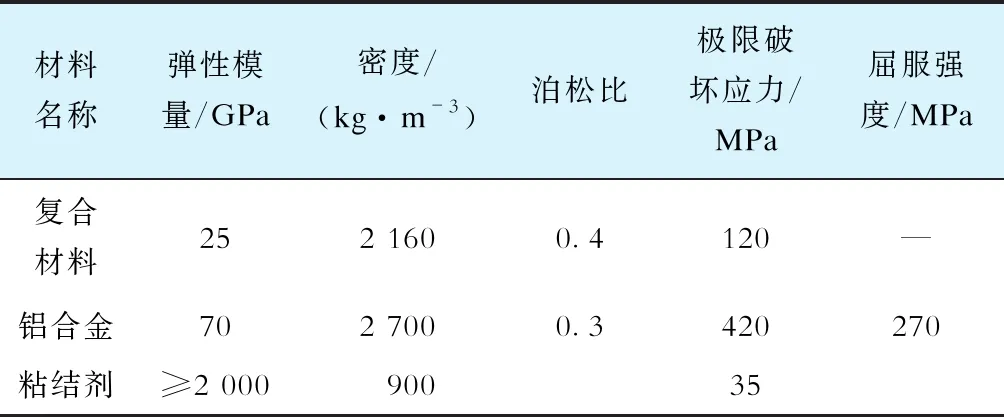
表1 材料主要力学参数Tab.1 Main mechanical parameters of materials

粘结剂成型后的理想粘接强度在200～300 MPa，但由于受到胶层内应力、气孔或缺陷、固化不完全、应力集中等因素的影响，粘结剂的实际粘结强度仅为理想状态下的10%～20%[25-29]，本文取最大粘结应力σmax为35 MPa。复合套管与金属法兰之间由粘结剂粘结，在对结构加载时可能会发生由于粘结剂撕裂导致的法兰与复合套管的粘结破坏，导致整体结构破坏过程是非线性的。材料本身的强度远远大于粘结剂的粘结强度，且发生粘结破坏时，2种材料的受力依然在线弹性范围内。同时，绝缘子大部分荷载都是由上向下传递，在下法兰节点处再由复合套管通过粘结层传向法兰，在粘结剂撕裂破坏前法兰很难发生塑性变形和局部开裂，为了重点探究法兰胶装节点非线性粘结破坏的全过程，不需要考虑金属材料的下降段本构，将2种材料的本构关系视为理想弹塑性本构。图2为复合支柱绝缘子几何尺寸。

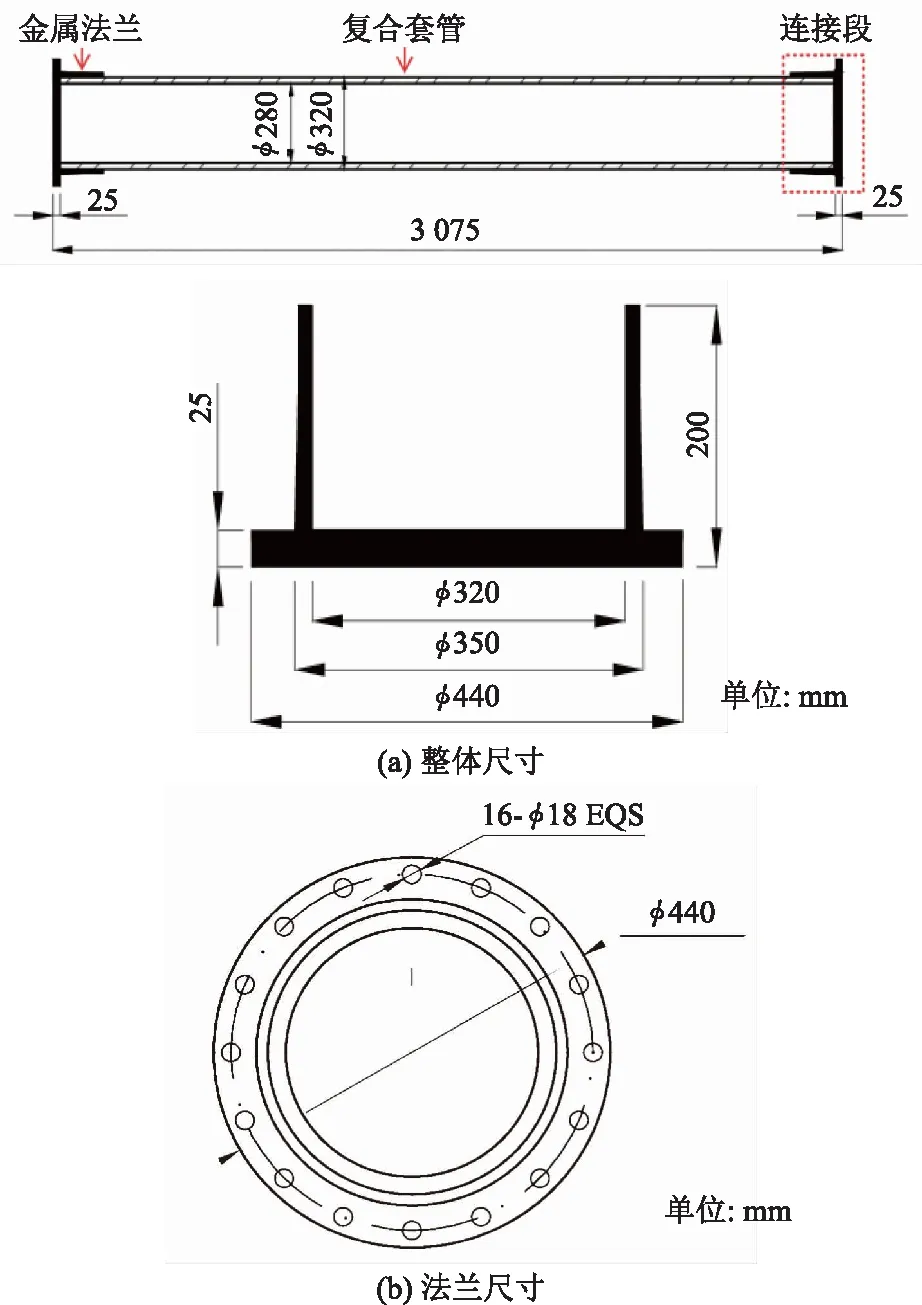
图2 复合支柱绝缘子几何尺寸Fig.2 Geometric dimensions of composite post insulator

1.2 有限元模型

本文采用大型有限元软件ANSYS对±800 kV单节复合绝缘子进行有限元建模和仿真受力分析。其中上下法兰、复合套管和粘结剂均用具有中节点的Solid95实体单元模拟，并全部采用六面体映射网格划分，法兰节点处进行局部网格加密，粘结层厚度取1 mm。网格划分后，分别在法兰内壁与粘结剂之间、粘结剂与复合绝缘子外壁之间插入0厚度的界面单元Inter204，用来模拟粘结层的附着和脱粘行为；插入粘结单元后再在法兰壁和粘结剂、粘结剂和套管之间定义接触对，使界面不发生分离时保持正常传力接触，接触算法采用增强拉格朗日法。通过建立内聚力材料(cohesive zone materials，CZM)来模拟胶装层的粘结破坏，CZM可以直接使用在界面单元Inter204上，并在CZM模型中定义粘结层最大分离应力等参数，实现对粘结剂开裂的模拟。采用文献[29]提出的对数形式CZM模型，这也是较为常用的内聚力材料模型，其中两粘结界面最大牵引力通过表面势定义。粘结破坏涉及界面分离，分离方向决定了破坏模式，包括垂直于界面分离(法向分离)和界面相切滑移(切向分离)。垂直于界面分离的界面法向临界牵引力分量Tn可由式(3)表示，通过联立式(1)和式(2)可消掉表面势，得到法向脱粘破坏时的界面临界牵引力Tn：

(1)

(2)

(3)

2 复合绝缘子法兰节点滞回性能

目前在国内外结构抗震试验中使用最为广泛的加载方法是控制位移的加载方法，这种方法以位移为控制值，以结构的屈曲位移为标准值，以此标准位移值的倍数作为加载的控制位移值。在本文的在滞回模拟中，采用位移控制，以绝缘子顶部为控制点，在下法兰底面设置全约束，采用静力单调加载方式。对于本文选取的复合绝缘子，厂家提供的额定弯曲负荷(specified cantilever load，SCL)为40 kN，且1 kN的线性位移为1.25 mm，则SCL对应出厂极限荷载Dmax为50 mm。为确定法兰破坏时的特征位移，首先规定各级荷载分别为25%Dmax、50%Dmax、100%Dmax、150%Dmax、200%Dmax，荷载每级加载为1圈，即往复加载循环1次，加载频率为0.5 Hz，为低周期往复加载过程。

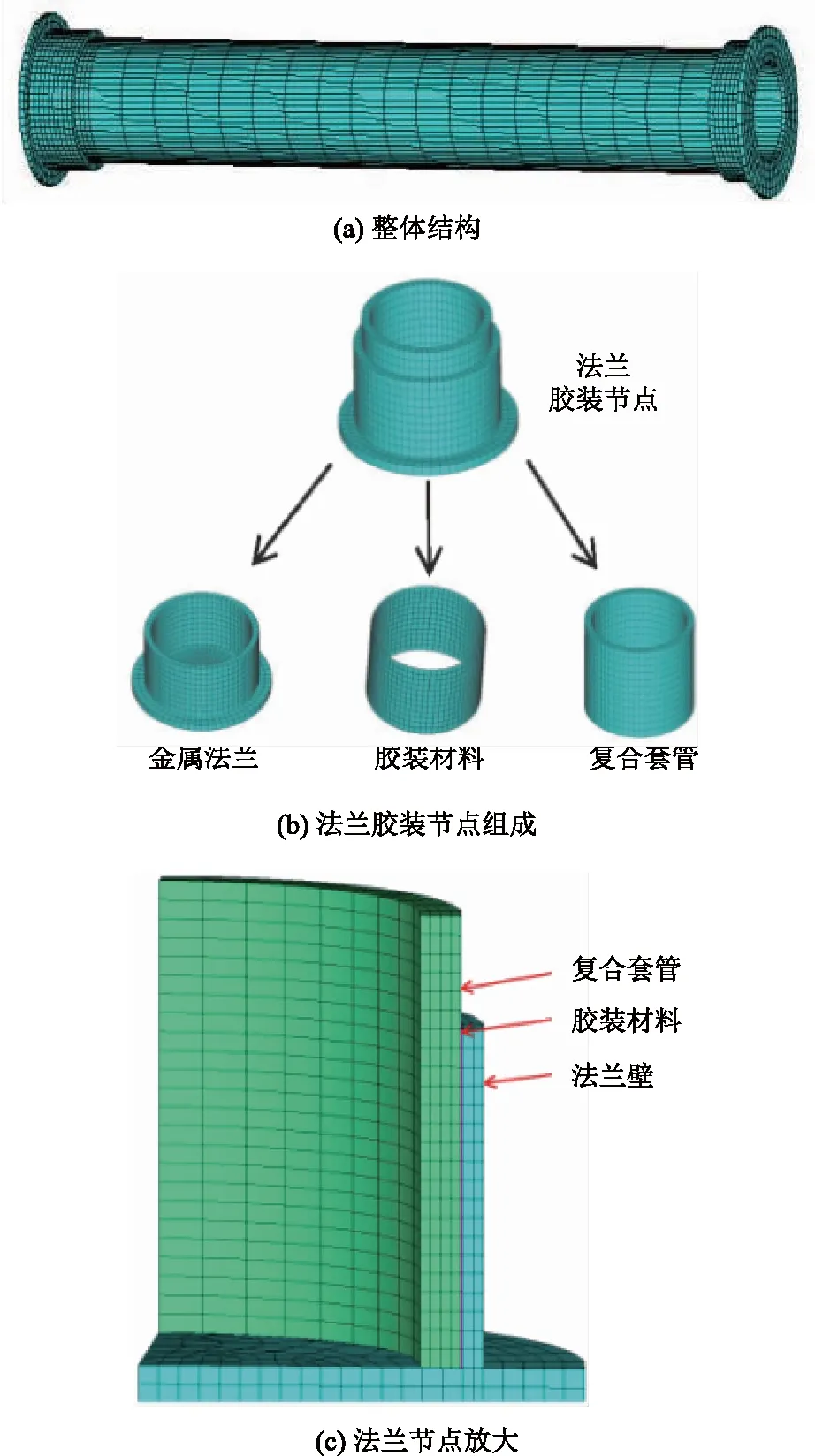
图3 复合支柱绝缘子有限元模型Fig.3 Finite element model of composite post insulator

图4为加载机制和复合绝缘子及法兰节点的滞回曲线，其中：A为加载位移；U为绝缘子或法兰节点的顶部位移；FV为结构所受水平力。

在实际工程中，粘结剂部分撕裂就可能导致复合材料电气设备在法兰节点处漏气。从绝缘子的承载极限状态考虑，可以某侧粘结剂沿法兰高度方向全部脱粘视为法兰节点破坏的依据，也作为整个绝缘子结构功能失效的标志。从图4(b)、(c)可以看出：法兰节点的滞回曲线饱满，但绝缘子整体结构耗能较差；法兰节点最大位移在6 mm左右，但滞回环饱满，耗能能力强。

本次模拟的目的是对比绝缘子整体和法兰节点局部的耗能能力，为得到法兰胶装节点准确的滞回曲线，应单独开展法兰节点的滞回模拟。法兰胶装节点加载机制、滞回曲线及节点胶体撕裂变形如图5所示。图5(a)所示加载机制为：0.5 mm、1 mm、2 mm、3 mm、4 mm、5 mm、6 mm。图5(c)为节点加载时的等效处理，将上部的绝缘子简化成刚性杆，仅用于传力，变形可以忽略不计。图5(b)为法兰节点滞回曲线，可以看出：法兰节点线性段位移较小，荷载小于SCL时胶体就已经开裂，开裂荷载为33.5 kN。由于绝缘子结构对称，且力作用点在结构对称轴上，因此下方结构也关于弯矩成轴对称，可取半结构观察法兰节点脱粘破坏情况。图5(d)为法兰节点脱粘失效时的水平变形云图，从图5(d)可以明显看出，在结构承受弯曲荷载时，受拉侧法兰壁与套管在节点发生脱粘破坏时出现了弯曲变形不协调的现象，法兰壁与套管的最大间隔出现在法兰最上部，也是粘结剂的最大水平开裂间距。

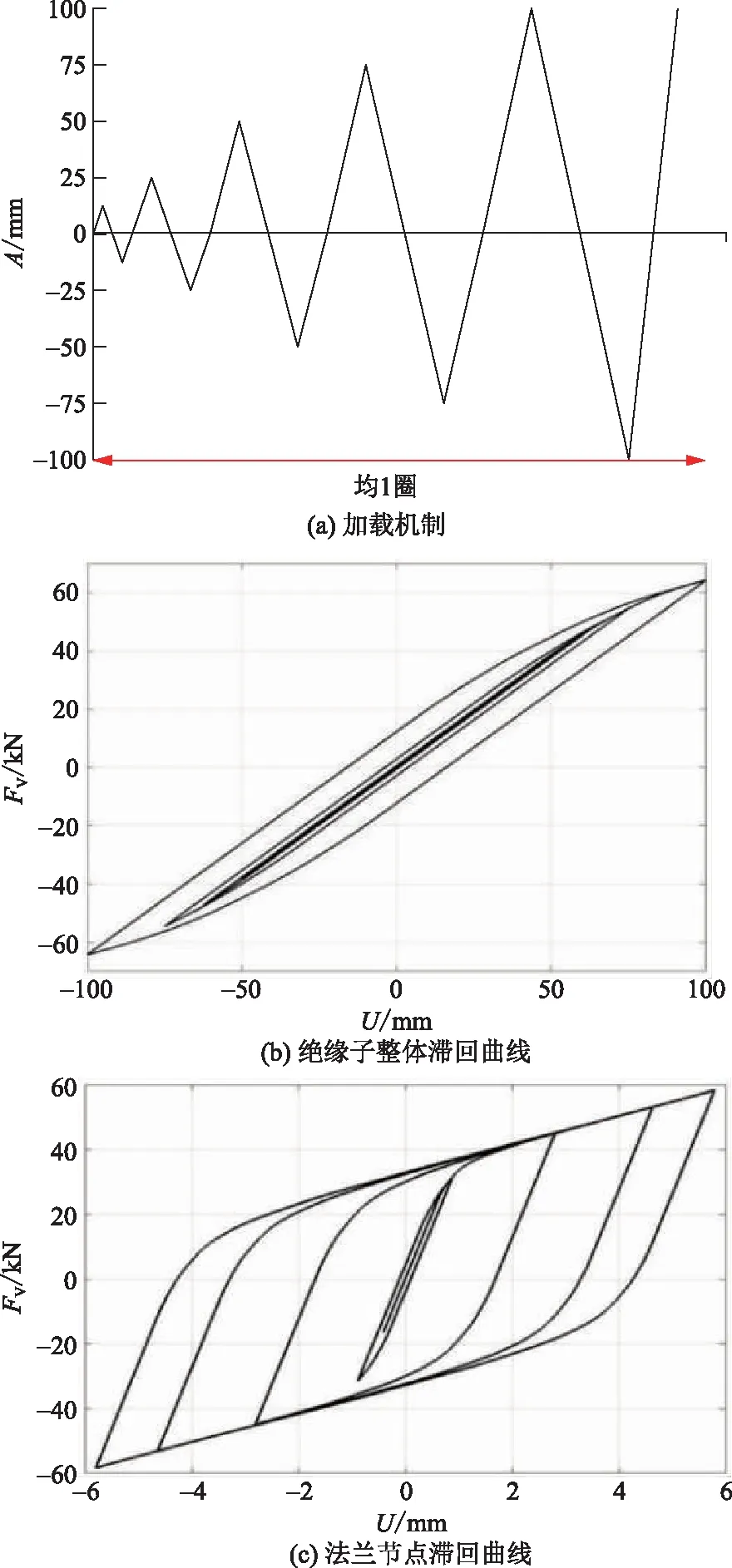
图4 复合绝缘子加载机制及滞回曲线Fig.4 Loading mechanism of composite insulator and hysteretic loop curves

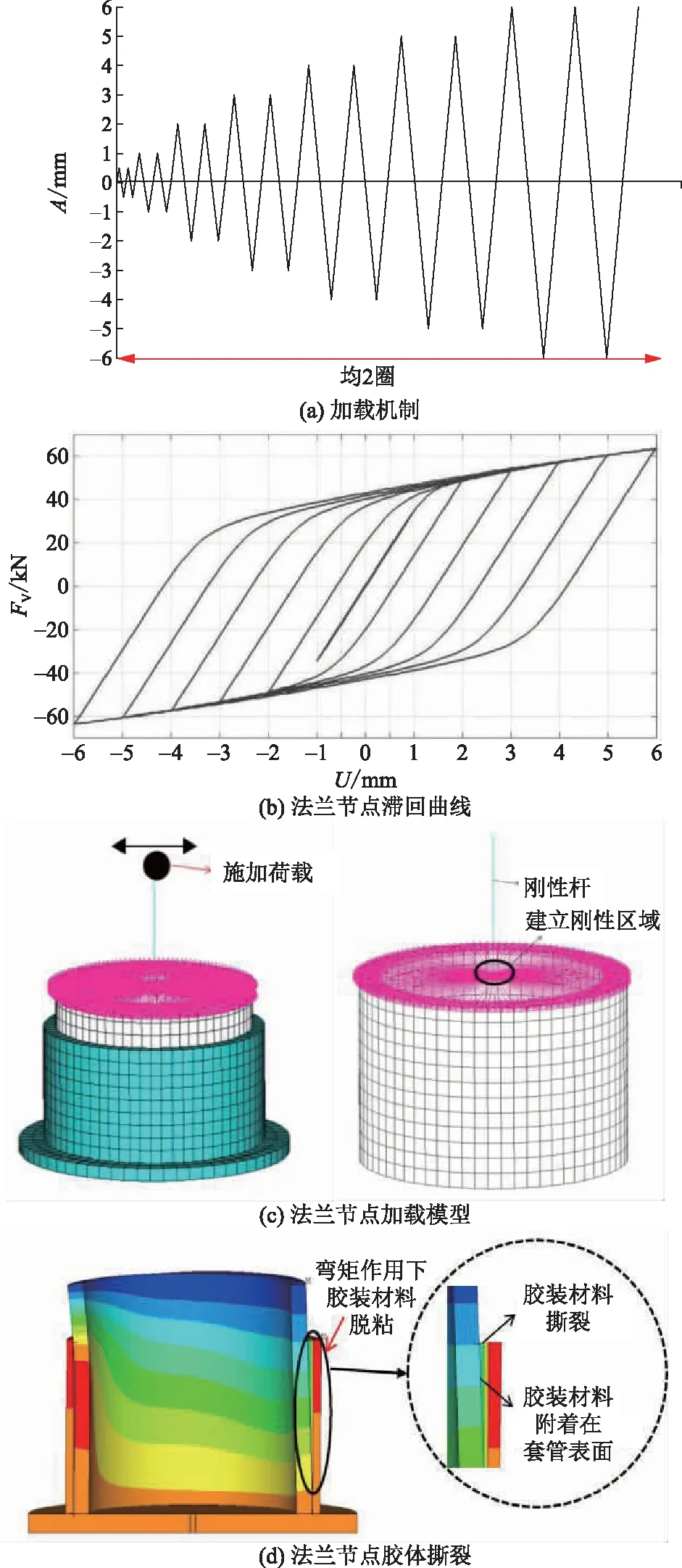
图5 法兰胶装节点加载机制、滞回曲线及节点胶体撕裂变形Fig.5 Loading mechanism and hysteretic loop curves of flange gluing joint and deformation of colloid

3 法兰节点设计参数对复合绝缘子抗震性能的影响

在实际工程中，电气设备上使用的复合绝缘子产品的尺寸及边界处受力情况均不同，所以应开展绝缘子不同物理参数和力学参数下的抗震性能分析。为此，选取关键设计参数和受力参数：法兰壁高度h、套管壁厚tb、粘结强度N。分别建立有限元模型进行参数分析，不同模型的参数见表2，加载模式为绝缘子顶部加载。各级荷载分别为12.5%Dmax、25%Dmax、37.5%Dmax、50%Dmax、62.5%Dmax、75%Dmax、100%Dmax，荷载每级加载为2圈。

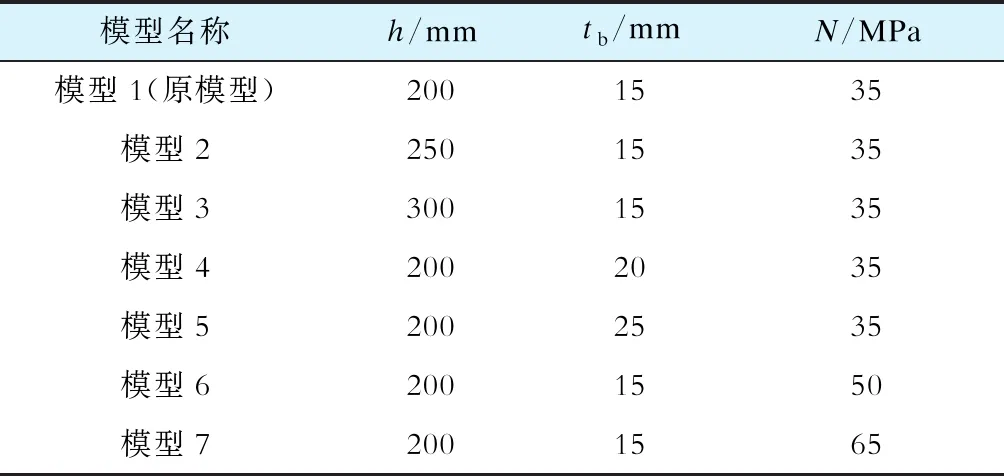
表2 模型参数及加载机制Tab.2 Model parameters and loading mechanism

3.1 滞回曲线

滞回曲线和骨架曲线是评价结构损伤程度、刚度退化以及承载性能的基础，也是计算延展性系数的主要依据，结构力-位移所围成的面积代表结构耗能的能量，反映了结构在地震作用下耗能能力的大小。从图6所示的滞回曲线可以看出，在开始加载时，滞回曲线围成的面积很小，曲线基本保持为线性，其耗能能力和残余变形都很少，是明显的弹性阶段。控制位移在37.5～50 mm。继续加载时，滞回环所包围面积增大，残余变形随之增大，刚度退化现象较为明显，这是弹塑性阶段。但是在极限控制位移为100 mm时，在7种模型中均发现承载力随着位移的增加而明显下降，说明复合套管的延展性较好。

从参数分析结果可以看出：增大法兰节点处的法兰壁高度对复合绝缘子承载力提升较小，但是对结构耗能能力提升较大；在控制位移增大时，结构的耗能能力明显增加，其极限承载力几乎不变，但是滞回环面积增大明显；增大复合绝缘子壁厚可以增加复合绝缘子的整体承载力，但是滞回曲线围成的面积增加较少，对结构的耗能能力提升不大，也说明复合绝缘子在破坏时复合材料处于弹性阶段，但是此时法兰节点已经破坏；增大法兰节点的粘结强度在线性段可以提升整体结构的整体刚度，同时耗能能力明显增加，当控制位移大于50 mm时，在相同位移下，粘结强度越大，复合绝缘子的耗能能力越大，但是当法兰节点开始破坏时，刚度迅速降低，出现了大位移的情况。

图6 滞回曲线Fig.6 Hysteretic loop curves

3.2 骨架曲线

图7为7种模型的骨架曲线。相较于滞回曲线，可更加明显看出：增大复合绝缘子的壁厚，可以明显提升结构的初始刚度，但是由于控制整体结构破坏状态的不是套管，而是法兰节点，所以在承载力不断增加时，整体结构的刚度下降速度也会增加；由于法兰节点高度增加，法兰节点破坏的裕度也会增加，即使法兰节点提前破坏，节点的剩余高度耗能能力也比原结构强，间接保证了复合绝缘子的承载力；增大法兰节点粘结强度，可以明显提升结构的延展性，但是由于节点发生破坏后，绝缘子的极限承载力会由法兰节点处粘结强度控制，控制位移增大，法兰节点虽然没有破坏，但是粘结接触面积会逐渐下降，复合绝缘子无法发挥本身承载力，但是结构在破坏时会有明显的征兆，节点的破坏时间也会延迟；增大粘结强度后，复合绝缘子整体结构的弹塑性特性更加明显。

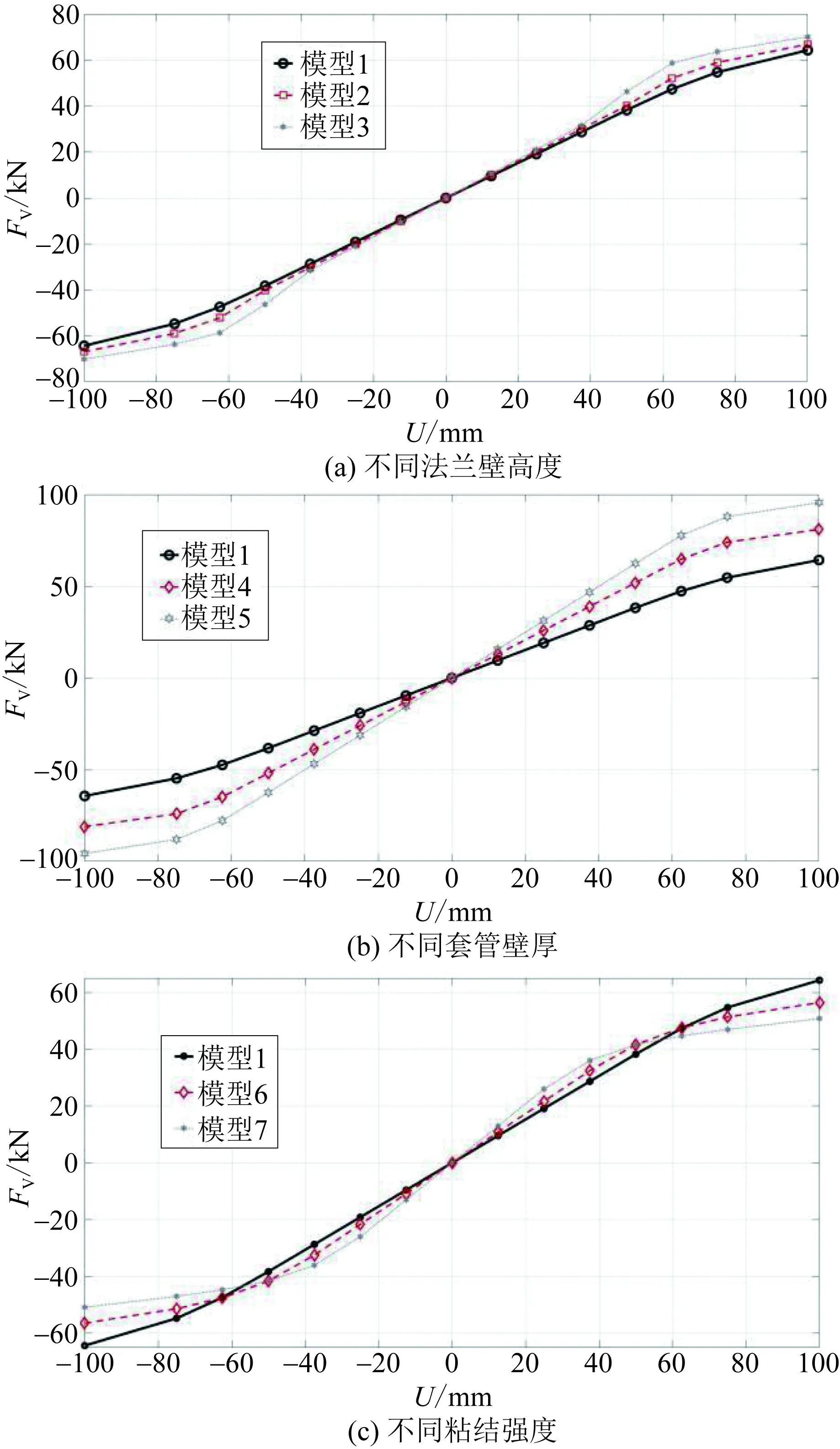
图7 骨架曲线Fig.7 Skeleton curves

3.3 等效粘滞阻尼比

等效粘滞阻尼比ζeq表示一个滞回环粘滞阻尼消耗的能量与弹性应变能的比值，等效粘滞阻尼比ζeq越大，结构的耗能能力越强，结构的抗震性能越好。等效粘滞阻尼比ζeq可以表示为

(4)

式中：S为滞回曲线围成的面积；E为系统的弹性应变能。

图8为7种模型的等效粘滞阻尼比。可以看出，在小位移范围内，绝缘子的耗能能力变化不大，但是在位移大于30 mm时，等效粘滞阻尼比随着位移增大而增大。由参数分析可知：增大复合绝缘子壁厚，耗能能力反而减小，说明复合绝缘子在往复运动耗能的过程中，首先破坏的不是绝缘子套管，也说明在相同位移下，抗力越大，耗能能力越小；增高法兰高度后，绝缘子的耗能能力会随之提升，说明结构最先发生破坏的是法兰节点处，但是过高的法兰壁使得法兰节点提前出现粘结裂缝，此时结构的耗能能力下降；增大法兰节点处的粘结应力，可以提升结构的整体耗能能力，但是结构的运动过程中会出现较大的位移，说明增大粘结强度会较大幅度提升绝缘子的延展性。

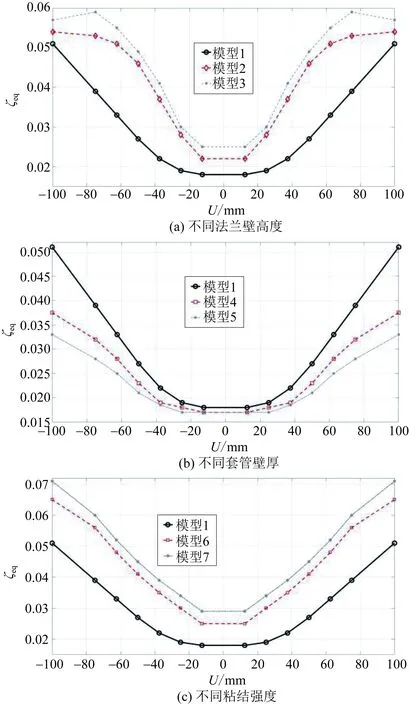
图8 等效粘滞阻尼比Fig.8 Equivalent viscous damping ratios

4 结论

本文以大直径复合绝缘子为研究对象，建立法兰节点的实体模型，并开展节点的抗震性能参数分析，得到以下结论：

a)法兰节点在往复运动中由于两侧胶发生胶体开裂，导致法兰胶装节点产生非线性力学行为。法兰节点先于其他所有构件开始耗能，说明法兰节点可提前屈服消耗地震能量，虽然保护上部主体结构没有受损，但是节点发生破坏会导致结构从根部开始发生倒塌。

b)适当增大复合绝缘子壁厚可以增加复合绝缘子的整体承载力，但是滞回曲线围成的面积增加较少，对结构的耗能能力提升不大；增大法兰节点处的法兰壁高度对复合绝缘子承载力提升较小，但是对结构耗能能力提升较大，在控制位移增大时，耗能能力明显增加。

c)增大法兰节点的粘结强度在线性段可以提升复合绝缘子的整体刚度，同时耗能能力明显增加，当控制位移大于50 mm时，在相同位移下，粘结强度越大，复合绝缘子的耗能能力越大，同时出现了大位移的情况。增大复合绝缘子壁厚，耗能能力反而减小，说明复合绝缘子在往复运动耗能的过程中，首先破坏的不是绝缘子套管，也说明在相同位移下，抗力越大，耗能能力越小。

d)增大法兰高度后，复合绝缘子的耗能能力会随之提升，也说明结构最先发生破坏的是法兰节点处，但是过高的法兰壁使得法兰节点提前出现粘结裂缝，此时结构的耗能能力会下降；增大法兰节点处的粘结应力，可以提升结构的整体耗能能力，但是结构在运动过程中会出现较大的位移，说明增大粘结强度会较大幅度提升绝缘子的延展性。