考虑分时电价机制的多微电网与主动配电网双层优化调度

吕智林，叶亮，孙功伟，廖庞思

(1.广西大学 电气工程学院，广西 南宁 530004；2. 广东电网有限责任公司佛山供电局，广东 佛山 528000)

微电网(microgrid，MG)作为清洁能源并网供电，已逐渐应用到大电网[1]中，它的出现改善了传统电网的固化运行方式；而随着分布式电源(distributed generation，DG)以MG形式接入配电网形成主动配电网(acitve distribution network, ADN)，提出了构建智能电网的新型模式。研究发现该运行模式可将DG以MG形式高渗透于ADN[2]，提高ADN系统的可靠性和调峰能力；另外MG接入ADN系统具有相互协调作用，包括[3]：①可以满足负荷需求，实现最优经济分配；②用电高峰/低谷时期出力协调；③紧急事故下可有效保障电力系统可靠运行。

多个MG接入ADN系统的优化调度研究多集中于ADN系统的经济调度，并且其经济调度模型一般采用集中式或分布式进行研究[4]；文献[5]对于ADN系统中新能源和负荷的随机特性，提出一种基于多场景技术的日前和实时调度两步走模型；文献[6]考虑MG并入配电网的博弈性影响，提出基于动态奖惩电价的含多MG的配电网分层协调优化调度模型；文献[7]考虑多MG系统的最优经济效益，提出了一种区域多MG系统的多目标优化调度模型并运用CPLEX对模型求解；对于MG接入ADN系统的多目标博弈性问题，文献[8]构建了ADN系统联合调度策略，建立MG和配电网双层模型并采用细胞膜-粒子群优化算法新型并行混合算法求解；文献[9]建立基于交替方向乘子法(alternating direction multiplier method，ADMM)的ADN分布式多目标优化调度方法，对含DG、柔性负荷及储能装置等多区域多目标优化调度模型进行求解。

以上文献未考虑多MG与ADN系统交互时，不同电价策略执行下及ADN系统网络拓扑结构中潮流约束对整个系统经济调度的影响。为解决不同利益主体约束下，平衡多目标的含多MGADN系统经济调度，本文考虑不同时段的电价差异、ADN系统潮流波动及MG中可控电源出力特性等，建立考虑分时电价机制的多MG与ADN双层优化调度模型。其中上层以ADN系统为对象，考虑系统的潮流约束及多MG与ADN间联络线的传输功率约束，建立以ADN系统经济成本最低为优化目标的数学模型并使用二阶锥规划(second order cone programming，SOCP)松弛技术与Gurobi工具求ADN系统最优潮流分布；下层以各MG系统为对象，考虑MG内功率平衡、可控电源出力特性及各MG买/卖电等约束，建立以MG运行成本最低为目标的并网MG调度模型，同时采用非支配排序遗传算法II (non-dominated sorting in genetic algorithm-II，NSGA-II)求解。最后以改进IEEE 33节点的系统为算例验证。

1 主动配电网模型

1.1 目标函数

上层模型中以ADN系统的各发电机组运行成本最小为优化目标，ADN系统中发电成本[10]

(1)

式中：T为周期(取24 h)；N为ADN系统网络结构中的总节点数；αi、βi、δi为第i个发电机组的成本系数；Pgi(t)为t时段第i个发电机输出的有功功率。系统网损

(2)

式中：M为接入MG数量；PPCCa(t)为t时段第a个MG买/卖电时公共联络线(point of common coupling，PCC)上传输的有功功率，若PPCCa(t)为正值表示MG向ADN买电，若PPCCa(t)为负值表示MG卖电给ADN；Pdi(t)为t时段节点i负荷有功功率。

1.2 约束条件

a) 系统的潮流方程如下：

(3)

式中：Pgi(t)、Qgi(t)分别为t时段节点i可控机组发出的有功功率、无功功率；QPCCa(t)为t时段第a个MG联络线传输的无功功率(忽略MG内的网损)；Qdi(t)分别为t时段节点i负荷无功功率；Ui(t)、Uj(t)分别为t时段节点i、j处电压幅值；Gij为ij支路电导；Bij为支路ij电纳；θij(t)为t时段节点i、j间相角差。

b) 各机组出力及各节点电压的约束如下：

(4)

c) 支路承受的最大功率约束：

|Ui(t)2Gij-Ui(t)Uj(t)(Gijcosθij(t)+

Bijsinθij(t))|≤Pij,max.

(5)

式中Pij,max为ij支路能承受的最大有功值。

d) 多MG与ADN间联络线传输功率约束如下：

PPCCa,min≤PPCCa(t)≤PPCCa,max.

(6)

式中：本文PPCCa(t)最大为200 kW；PPCCa,max、PPCCa,min分别为联络线传输功率的上、下限。

2 并网MG模型

2.1 可控电源与蓄电池模型

a) 柴油发电机。柴油发电机(diesel engine,DE)是MG中重要的调峰单元，也是文中可控电源里唯一可以产生无功的机组，其发电特性与传统发电机能耗特性相似，均可采用二次函数模型[11]：

(7)

式中：Vf为DE以输出功率Pde工作Δt时间的耗油量，单位kg/(kWh)；Δt为时间间隔，取值为1 h；ηde为DE的发电效率，取值为30%；Lf为柴油低位热值，取为43.1 GJ/kg；a1、a2、a3分别取为2.66 7、0.163 7、0.000 15。

b) 微型燃气轮机。微型燃气轮机(micro turbine,MT)是一种具有运行稳定、占地面积小等优点的可控电源。假设MT机组中的MT、溴冷机排烟温度始终保持不变[12]，其函数模型为

Vmt=∑PmtΔt/(ηmt·Ζg).

(8)

式中：Vmt为天然气的耗量；Pmt为MT发出的有功功率；Ζg为天然气低位热值，取9.7 kWh/ m3；ηmt为MT发电效率，取值为29%。

c) 储能蓄电池。文中采用铅蓄电池作为储能装置，电池的剩余容量与上一时刻剩余容量、当前时刻放电量及蓄电池衰减量密切相关[13]；蓄电池荷电状态(sate of charge，SOC)的表达式为：

(9)

式中：Ssoc(t)为t时刻蓄电池荷电状态；Pch(t)为t时刻蓄电池充电功率；Pdis(t)为t时刻蓄电池的放电功率；∂为蓄电池自放电率，一般取值为0.2%/h；μch、μdis分别为蓄电池充、放电效率；Ees为蓄电池装机容量(kWh)。

2.2 目标函数

MG中的风力、光伏发电属于可再生能源，对其设置为优先调用，以MG的运行成本最小为目标，其数学模型为：

C=min(FGe+Fes-Fb-s),

(10)

(11)

(12)

Fb-s=Fbuy+Fsell,

(13)

(14)

式(10)—(14)中:C为MG运行成本；FGe为MG中可控机组的运行成本；Fes为蓄电池充放电时的折旧成本；Fb-s为MG向ADN买/卖电的收益；R为MG中可控电源总数；ψma,k、ψf,k分别为可控电源k的运行维护、燃料成本系数；Pk(t)、Vf,k(t)分别为t时段可控电源k有功出力、燃料消耗量；Pes(t)、λ(Pes(t))分别为t时段蓄电池充放电功率、充放电折旧成本系数[14]；Fbuy为MG向ADN买电的所需成本；Fsell为MG向ADN卖电获得的收益；cbuy(t)、csell(t)分别为t时段买、卖电的基础电价；PPCC(t)为t时段联络线有功功率；Pbuy(t)为t时段MG买电功率；Psell(t)为t时段MG卖电功率。

2.3 约束条件

a) 系统功率平衡约束为：

Ppv(t)+Pwt(t)+Pde(t)+Pmt(t)+PPCC(t)=

Pmg,load(t)+Pch(t)-Pdis(t).

(15)

式中：Pwt(t)、Ppv(t)、Pde(t)、Pmt(t)、PPCC(t)分别为t时段风力发电机、光伏发电机、DE、MT、联络线的有功功率；Pmg,load(t)为t时段MG内负荷有功功率；Pch(t)、Pdis(t)分别为t时段蓄电池充、放电有功功率。

b) 可控微电源出力约束为：

Pmin≤Pk(t)≤Pmax.

(16)

式中：Pk(t)为可控微电源k在t时段有功出力值；Pmin、Pmax分别为可控微电源有功出力的最值。

c) 可控微电源的爬坡约束为：

(17)

式中：Pup,k(t)、Pup,k(t-1)分别为可控微电源k在t、t-1时段上升后的有功值；Pdown,k(t)、Pdown,k(t-1)分别为可控微电源k在t、t-1时段下降后的有功值；Rup,k、Rdown,k分别为可控微电源k最大爬坡率、下坡率。

d) 蓄电池充/放电功率约束为：

蓄电池过充或过放会降低其使用寿命，其充/放电时荷电量需满足约束条件，数学模型[15]为

Ssoc,min≤Ssoc(t)≤Ssoc,max.

(18)

式中：Ssoc,min、Ssoc,max分别为蓄电池最低荷电量、最高荷电量。蓄电池长期在过高功率环境下运行，也对电池的寿命有影响。

3 双层模型求解

3.1 ADN模型的求解

大型电力系统中的最优潮流问题是非凸非线性的潮流问题，传统智能优化算法难以求得其全局最优。本文采用SOCP松弛技术[16]对ADN系统中的非凸非线性最优潮流模型进行改善，将其转化为凸可行域内的线性潮流模型再求解。ADN系统的非凸非线性特性主要来自如下表达式：

(19)

式中ei、fi为节点i处电压向量的实部与虚部。对每个节点及节点之间分别新定义变量cii、cij、sij，通过转化形成新导纳矩阵的对应元素，根据决策关系它们必须满足如下关系：

(20)

将式(19)、(20)代入式(3)中进行等价变换，得出ADN系统新的最优潮流平衡方程，对于其他各约束条件中的等价变换具体转换步骤见文献[16]。

(21)

式中Ω(i)为以节点i为末端的新末端节点集合。转化后的各等式和不等式约束方程通过MATLAB编译器写出优化程序并正确调试，最后调用Gurobi工具包求解ADN系统最优潮流分布。

3.2 并网MG模型的求解

并网MG优化调度策略按照峰时段MG多售电，谷时段和平时段多购电的原则(谷时段为00:00—07:00，平时段为08:00—10:00、16:00—18:00和22:00—23:00，峰时段为11:00—15:00和19:00—21:00)进行最优调度。依据分时电价机制的调度策略[17]确定蓄电池充/放电功率及MG与ADN的交换功率，达到整个系统稳定运行。

传统遗传算法求解并网MG模型时，易陷入局部最优解且难以求得精确数据。为此本文采用NSGA-II[17]求解MG模型，主要对算法作出以下改进：

a)Tent混沌映射。Tent映射是分段性映射技术，具有均匀概率密度和遍历性等特性。本文利用Tent映射所构建的混沌变量，将变量映射到优化量空间中对种群进行初始化，改变个体多样性。Tent映射数学模型为：

(22)

式中hn为第n次迭代变量，形成的序列中可能有不稳定点，于是需要利用小值扰动跳出该类不动点。改进后Tent混沌映射数学模型为：

(23)

式中r(0,1)为0～1间的随机数。

而根据式(23)对种群中每个染色体均会生成一个混沌序列ρ，将其映射到决策变量的取值范围内后，则第a个染色体x的第b维分量

(24)

这一创新做法，从2013年起连续6年被写入安徽省委一号文件，2017年被原农业部等六部委联合发文向全国推广，2018年被写入中央一号文件。为抓好政策扶持和配套服务，宿州市委、市政府出台了《关于扶持农业产业化联合体发展的若干政策意见》等文件，市、县区两级财政每年兑现产业化联合体成员各类奖补资金3600多万元。

b)NDX算子。引入NDX算子提高空间搜索能力，其寻优能力极强，易使寻优解跳出局部解。NDX算子交叉后新的数学模型为：

(25)

式中：x1,b和x2,b分别为交叉后的父代染色体第b维分量；y1,b和y2,b为交叉后产生的子代染色体第b维分量；Φ为NDX算子交叉过程中产生的随机数，其值在(0,1)间均匀分布；|N(0,1)|为正态分布随机变量。

3.3 分时电价下MG层对ADN层的求解流程

考虑分时电价机制的多MG与ADN双层优化调度模型求解过程可以分为2部分：第1部分(并网MG的优化调度)为基于分时电价机制的MG优化调度策略下，建立并网MG优化调度模型，并运用NSGA-II求解模型，分别求出可控微电源出力、MG买卖电功率及各MG的运行成本(取MG中风/光等可再生能源出力及负荷消耗功率的预测数据作为输入值进行优化分析)；第2部分(含多MG的ADN优化调度)根据多MG向ADN买卖电时联络线传输功率的制约，以ADN系统中各发电机组的运行成本最小为目标建立ADN系统最优潮流模型，运用SOCP松弛技术对模型进行线性化处理，将非线性潮流问题转化为线性潮流问题，再调用MATLAB软件中的Gurobi求解器求出ADN系统的最优潮流分布。分时电价下的双层优化调度模型求解流程如图1所示。

4 算例验证

为有效验证所提双层优化模型的可行性，本文选用改进IEEE 33节点的ADN系统作为算例(如图2所示)，在MATLAB2016a环境下实现模拟仿真(i5，2.3 GHz，4 GB)。发现MG并入位置不同，负荷的分布也不同；在24 h调度周期内，解ADN系统最优潮流所需平均时间为1.25 min。MG1中的柴油发电机(DE1)、微型燃气轮机(MT1)与和MG2中的柴油发电机(DE2)、微型燃气轮机(MT2)出力技术参数见表1，MG与ADN系统买卖电的电价见表2。上层ADN系统网络拓扑结构中各参数详见文献[18]，ADN系统各机组发电特性见文献[18]。整个系统调度周期内，各MG中风力、光伏及负荷预测数据来自文献[19]。

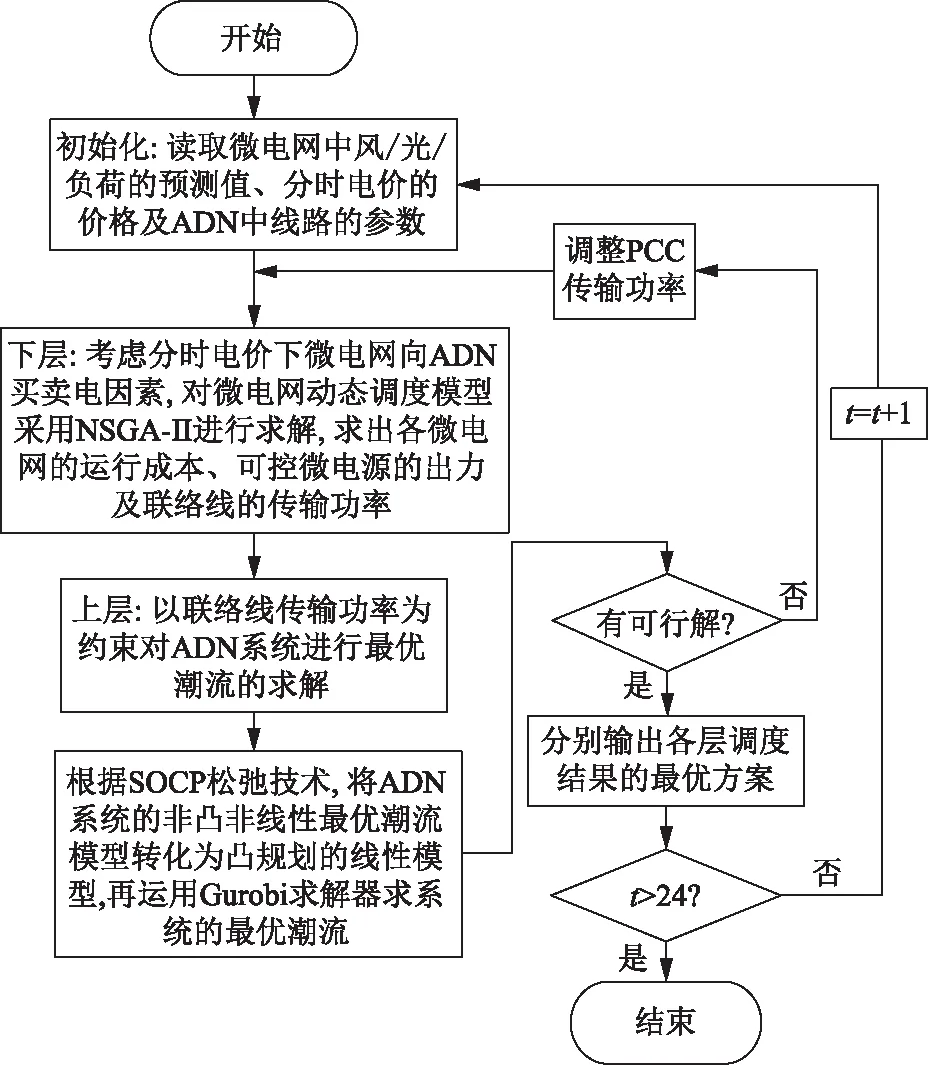
图1 分时电价下的双层优化调度模型求解流程Fig.1 Flow chart of solving bi-level optimal scheduling model under TOU

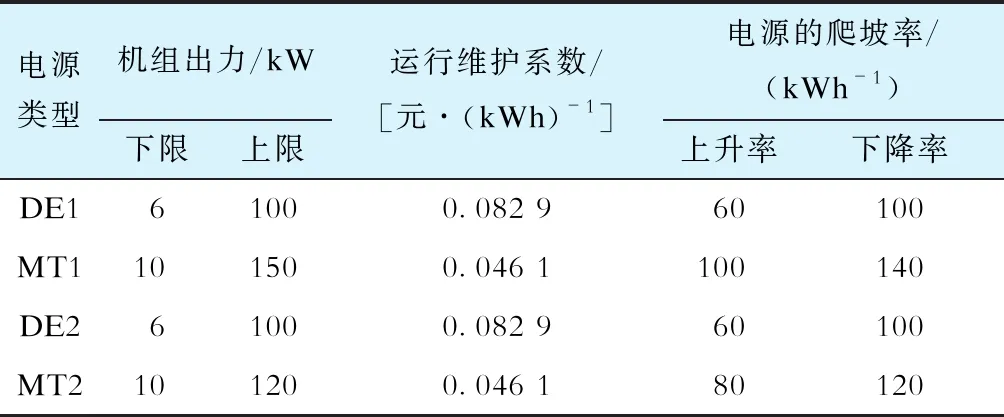
表1 可控电源技术参数 [20]Tab.1 Technical parameters of controllable power supply

表2 MG买电与卖电电价[21]Tab.2 Electricity purchase and sale prices of microgrid

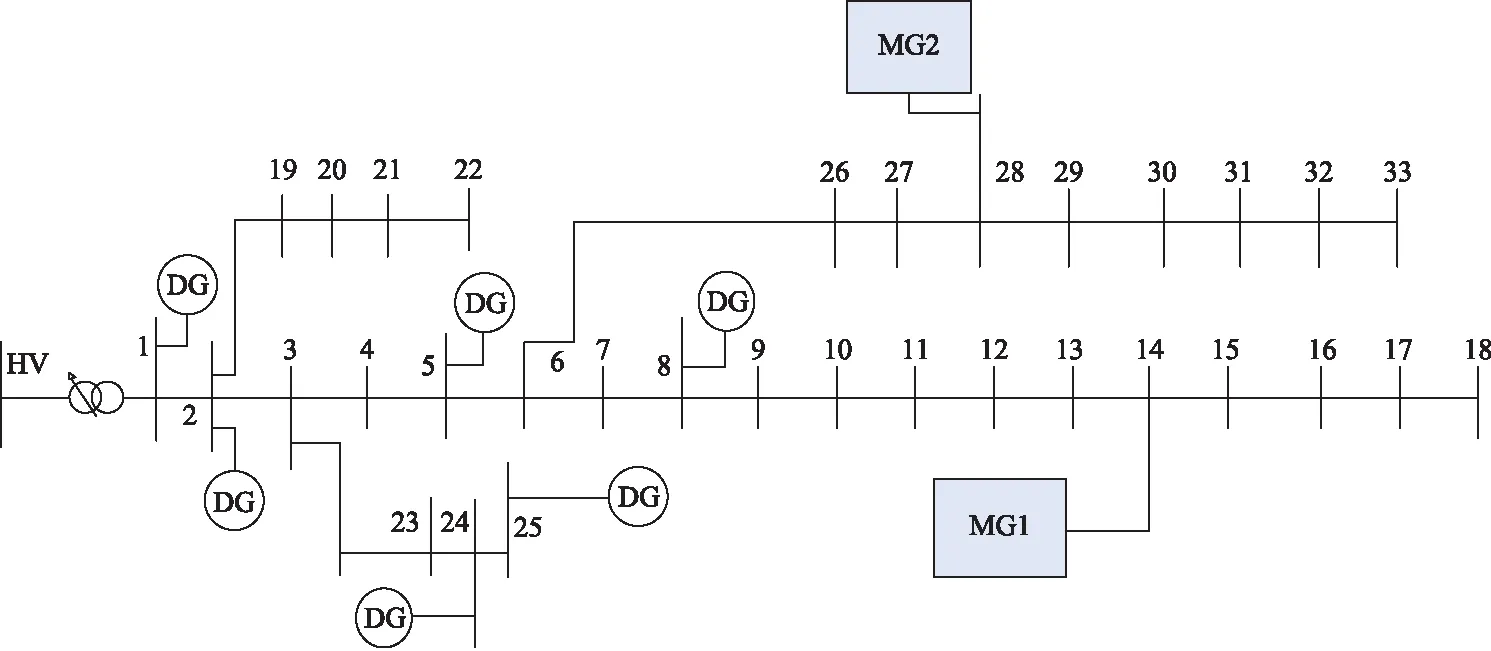
图2 含多MG的ADN系统结构Fig.2 ADN system structure with multi-microgrids

上层模型中负荷预测值为某城市地区1 d内的变化情况；在各MG中风力、光伏及负荷取值为某小区预测值。下层模型中NSGA-II相关参数：迭代次数kmax=200，种群规模Si=100，交叉和变异概率Pe=0.9,Pm=0.1。

4.1 并网MG层调度结果

根据分时电价下的双层优化调度模型求解策略要求，采用改进遗传算法对各并网MG的优化调度模型求解，分别求解得到各MG中DE、MT、负荷(Load)、SOC的最优值并绘制调度结果，如图3、4所示。

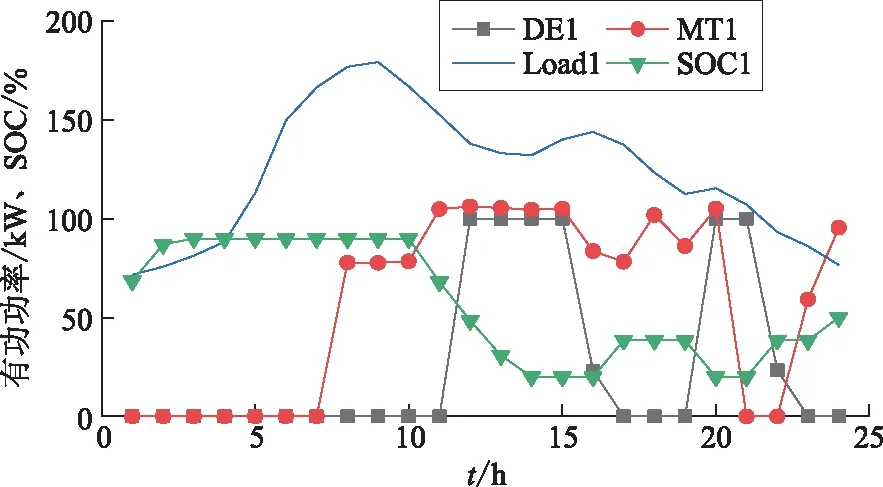
图3 MG1优化调度结果 Fig.3 Optimized scheduling results of MG1

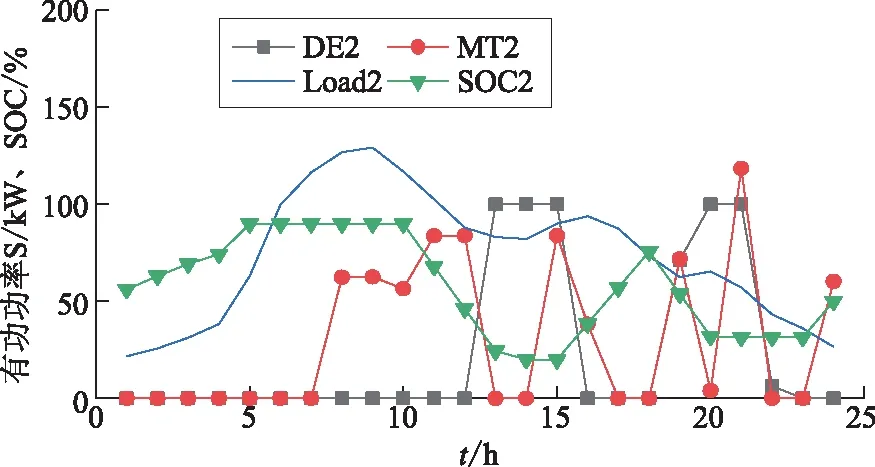
图4 MG2优化调度结果Fig.4 Optimized scheduling results of MG2

从图3和图4可以看出，1—4时段内由于MG1中风/光出力无法满足用电负荷的需求且MG内上午可控机组出力成本高于MG买电成本，根据MG的优化调度策略此时MG向ADN买电，并尽可能将蓄电池充电至饱和，以降低MG的运行成本；MG2中用电负荷需求低，此时风/光出力可以满足MG系统的稳定运行，所以MG2不买电且可控机组不动作。在5—10时段内，负荷达到高峰期而风/光出力跟不上负荷增长需求；在16—18时段内，风/光出力无法满足负荷的需求；在22时段内负荷虽然没有达到高峰，但出现风光出力骤减；在这些时段内根据优化调度策略，均需通过储能系统放电、可控机组出力以及向ADN系统买电来满足用电负荷的需求。在风/光发电充足时段或峰时段分时电价机制下，MG可在综合考虑运行成本的约束下，将优化出的多余功率卖给ADN，使得MG获得卖电收益(如11、15和23时段等)。

根据分时电价下的双层优化调度模型求解策略要求，采用改进遗传算法对各并网MG的优化调度模型求解，分别求解得出各MG的买卖电情况和各MG的运行成本情况并绘制调度结果，如图5、6所示。

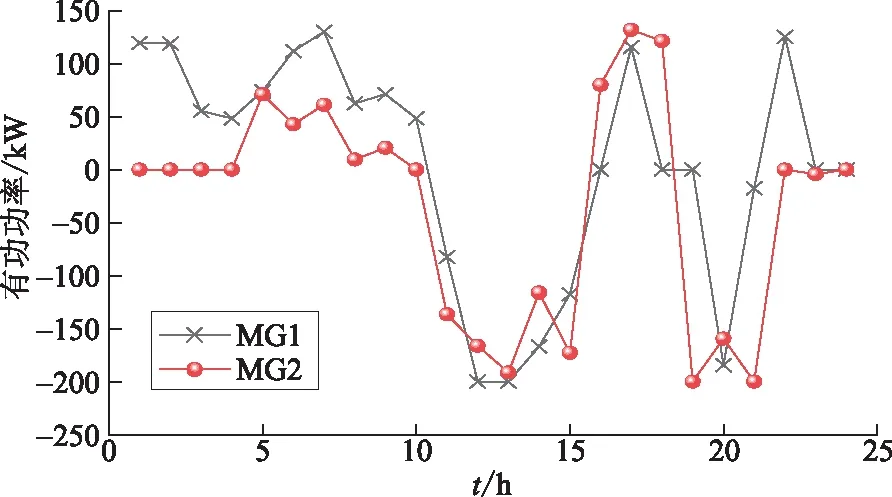
图5 MG向ADN系统的买/卖电功率 Fig.5 Buying/selling power of microgrid from ADN system

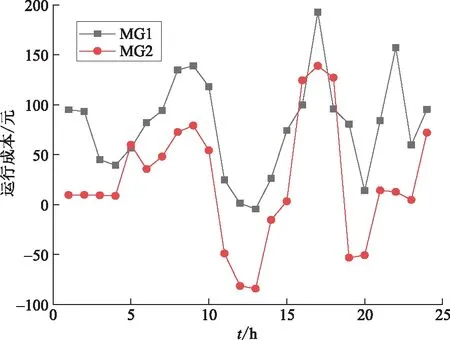
图6 2个MG的运行成本Fig.6 Operating costs of two microgrids

从图5和图6可以看出，多MG与ADN系统功率交互时，各MG内部负荷需求不同，导致其向ADN系统买/卖电功率不同(正值为MG向ADN买电功率，负值为MG向ADN卖电功率)。各MG的运行成本曲线与其买/卖电功率曲线的关系为正相关(正值为买电花费的费用，负值为卖电获得的收益)。

4.2 ADN层调度结果

根据分时电价下的双层优化调度模型求解策略要求，对于ADN层的最优潮流模型求解，采用Gurobi求解器对转换后的凸优化潮流模型进行求解，分别求出ADN系统网络中各机组出力和各节点电压标幺值并绘制调度结果，如图7、8所示。

图7 ADN中各机组出力及负荷预测值Fig.7 Output and load prediction values of each unit in ADN

从图7和图8可以看出：考虑多MG买/卖电因素时，在ADN系统优化调度过程中，8号、24号和25号机组后分支负荷较多，此类机组出力较大。根据ADN系统最优成本约束，在峰时段多MG向ADN卖电时，8号和25号机组出力有所降低，起到了削峰作用；其他各机组协调出力来共同维持ADN系统稳定运行。ADN系统中各节点电压随着输电距离的变化会有所波动，但其远端节点电压的标幺值均保持在可控范围内波动(0.93～1.06)；当多MG向ADN买/卖电时功率出现波动时，并不会影响ADN系统的稳定运行。

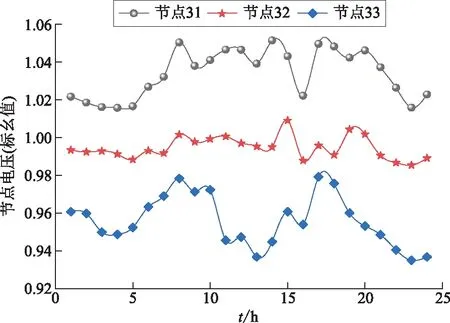
图8 ADN中远端节点电压Fig.8 Voltage at the far end of ADN

4.3 含多MG的ADN系统层调度结果

根据分时电价下的双层优化调度模型求解策略要求，求出ADN系统的经济成本及网损。为进一步体现本文所提策略及算法的优势(情景模式3)，分别设立了情景模式1与情景模式2：情景模式1为多MG不参与原ADN系统的优化调度，各自独立优化运行；情景模式2为多MG与原ADN系统通过联络线进行功率交互，实现能源最大化利用，但未考虑动态电价对原ADN系统的经济成本影响。根据各情景模式下的ADN系统优化调度结果绘制曲线，如图9、10所示。

图9 ADN系统的经济成本 Fig.9 Economic cost of ADN system

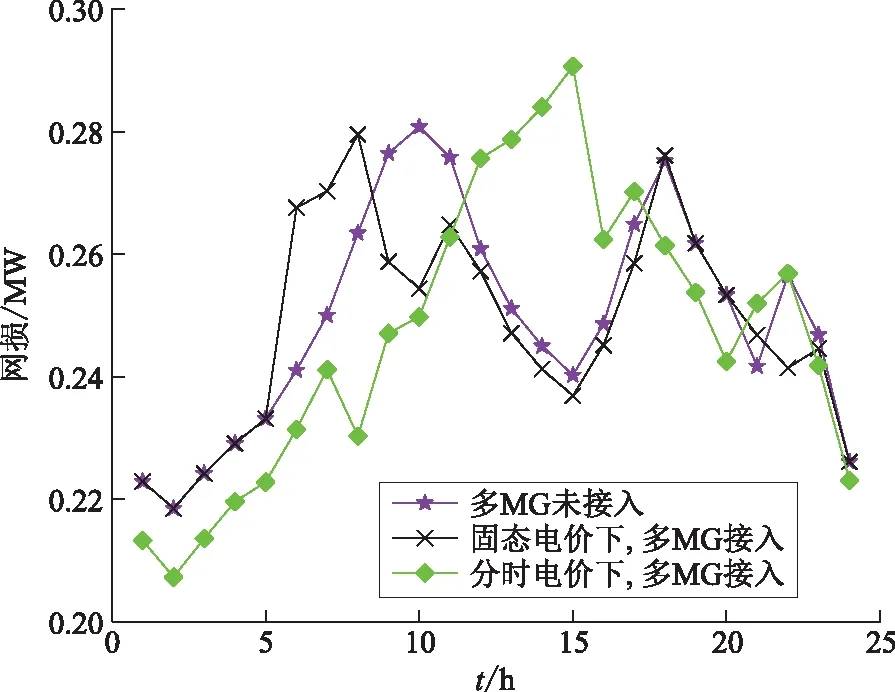
图10 ADN系统中的网损Fig.10 Network loss of ADN system

从图5和图9可以看出，在情景模式3分时电价下，含多MG的ADN系统经济调度结果中：当多MG处于买电状态时，ADN中各机组会根据优化算法而选择增加机组的出力，所以多MG接入ADN系统时ADN运行成本会有所增高；当多MG处于卖电状态时，MG卖电时段可以削减ADN中负荷对电能的消纳，从而减少ADN系统各机组出力，降低系统经济成本。从图5和图10中可以看出，情景模式3分时电价下含多MG的ADN系统经济调度结果中：当多MG处于买电状态时，MG看作虚拟负荷，此时ADN中各机组会根据优化算法增加出力，导致网损增多。当多MG处于卖电状态时，MG看作虚拟电源出力，可就近供电至ADN中负荷消纳，从而减少ADN系统机组出力，使系统网损有所降低。

统计24个时段内含多MG的ADN系统经济调度结果见表3。通过与情景模式1、2相比可以发现，采用情景模式3对整个系统进行经济调度时，系统的经济效益最佳。

表3 含多MG的ADN系统经济调度Tab.3 Economic scheduling of ADN systems with multi-microgrids

5 结束语

本文对含多MG的ADN系统的经济性进行研究，考虑多MG向ADN买/卖电及ADN系统中最优潮流等约束，建立分时电价机制下的多MG与ADN双层优化模型。以改进IEEE 33节点配电网系统为算例进行验证，结果表明所提模型及算法具有可行性且可以降低含多MG的ADN系统网损和经济成本。对于ADN层而言，当多MG向ADN卖电时，ADN层可以减少其他机组的出力，降低ADN系统的经济成本；反之当多MG向ADN买电时，ADN层通过卖电获得收益。对于MG层而言，当MG内可再生能源出力不足时，根据分时电价下的最优调度策略，可通过对储能系统放电、向ADN买电和调用可控机组出力来满足负荷需求，保证MG稳定优化运行；当MG内可再生能源出力充足有余时，可向ADN系统卖电获得收益。

本文所提模型及求解方法对未来大规模的MG并网供电具有一定的理论参考价值，同时为电力市场更好定电价有指导意义。