荧光法测定半导体禁带宽度*

时凯居 李睿 李长富 王成新 徐现刚 冀子武†

1) (山东大学微电子学院,新一代半导体材料研究院,济南 250100)

2) (山东浪潮华光光电子股份有限公司,潍坊 261061)

1 引言

光学带隙或禁带宽度是半导体的一个重要特征参数,它反映了价电子被束缚的强弱程度和半导体光学性能的优劣,同时决定了激发该半导体所需要的最小能量[1-3].因此,在光学研究中,测定一种新型半导体材料的光学带隙对于了解其结构特性、光学特性和实际用途具有重要的物理意义和现实意义.目前,常用的光学测试方法主要有吸收光谱法(或透射光谱法)[4-6].该方法因操作过程简单易行,而被相关研究者广泛采用.然而,在实际应用中吸收光谱法也存在着一些难以克服的缺点:1)对于生长在窄带隙衬底上的外延材料或结构,还必须事先进行衬底剥离才能进行测量,但这个剥离过程耗时费力,并有可能导致样品的损伤甚至损坏;2)如果外延层是由不同带隙的多层材料组成的复合结构,那么其他层的吸收也会对目标层的测量造成不可忽视的干扰;3)利用公式αhν=A(hν-Eg)p[4]对实验测得的透射谱的吸收边进行拟合以确定能量带隙时,有时会因为吸收边的不规则而难以完美拟合,并因此造成较大的测量误差[5],这里α,hv,A,Eg和p分别为吸收系数、入射光子能量、比例系数、禁带宽度和由半导体类型所决定的常数;4)由于上述测量使用的是宽光源,相应波长的输出功率较小,这样也会影响测量精度[6].

荧光(光致发光(photoluminescence,PL)或电致发光(electroluminescence,EL))测量是研究探讨半导体发光材料或器件结构特性和光电特性不可或缺的重要手段[7,8].利用荧光法测定半导体材料的带隙宽度,在一定程度上可以克服透射光谱法的固有弊端,同时也能够深入地洞悉该材料的结构特性与光学特性的内在关联,揭示载流子的产生、传输和复合发光过程的动力学机制[9,10].因此荧光法也是测定半导体带隙宽度的一个理想候选方法,并且已经有许多研究将荧光峰位能量默认为禁带宽度并结合费伽德定律(Vegard’s law)计算出相关的结构参数[11-14].然而,上述将荧光峰位能量简单地看作是禁带宽度的做法并不十分妥当,因为在很多情况下,样品结构的不完美会导致峰位能量与禁带宽度之间出现较大的偏差.众所周知,由于生长工艺的不成熟以及合适衬底的缺乏,致使所获得的半导体材料的结晶质量或结构质量不够完美,如杂质/缺陷相关的非辐射中心的存在[15,16],多元合金中组分起伏相关的局域中心的存在[17,18],以及异质结构中晶格失配所诱发的量子限制斯塔克效应(quantum confinement Stark effect,QCSE)的存在等[19,20].这些因素都会使辐射能量发生红移并导致测量结果和实际带隙(即本征带隙)之间存在较大的偏差,即所谓的斯托克斯位移.因此,如何优化荧光测试条件以减小或避免上述因素的干扰或影响,是获得较为精确测量结果的关键.

光学带隙也是温度的函数.对于本征半导体,它遵从瓦氏尼定律(Varshni law),即依赖温度的禁带收缩效应[21,22].本文采用荧光测量方法,重点探讨了典型目标温度下具有代表性结构特征的半导体带隙测定应满足的测试条件,即常温(300 K)条件下InGaN/GaN 多量子阱结构中InGaN 阱层的光学带隙测定应满足的测试条件,以期获得较为精确的光学带隙测量结果.

2 实验方法

本研究所涉及的几个样品(包括绿光样品SG1、SG2以及蓝光样品SB)均为基于InGaN/GaN多量子阱(MQWs)结构的发光二极管(LED),并且都是通过金属有机化学气相沉积方法在蓝宝石衬底或硅衬底上外延生长而成.其制备过程简述如下:以三甲基铝(TMAl)、三甲基铟(TMIn)、三甲基镓(TMGa)、氨气(NH3)、硅烷(SiH4)和二茂镁(Cp2Mg)分别作为Al,In,Ga,N,Si 和Mg 的源,并且在衬底上依次生长低温成核层、非故意掺杂的GaN 层、Si 掺杂的n 型GaN 层、InGaN/GaN MQWs 层(即有源区)、Mg 掺杂的p-AlGaN 电子阻挡层和p-GaN 接触层.芯片面积为1.16 mm ×1.16mm,样品结构及具体参数分别如图1 和表1所示(具体细节可参见文献[23-26]).

表1 样品的具体参数Table 1.Specific parameters of samples.

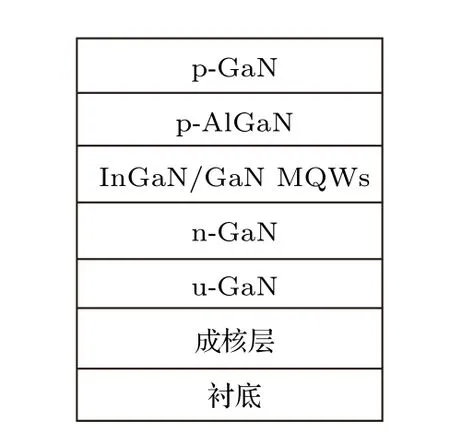
图1 样品结构示意图Fig.1.Schematic diagrams of samples.

研究所涉及的与上述样品相关的EL 数据,都来自本课题组之前的研究工作[23-26].主要包括:不同注入电流下EL 谱的温度依赖性;目标温度(300 K)下EL 谱的注入电流依赖性.对于上述EL谱的温度依赖性和注入电流依赖性测量,样品被置于封闭循环液态氦(He)制冷的样品室内,温度可调范围为6—350 K.一个Keithley 2400 源表被用作激发电流源,可调电流范围为0.01—350.00 mA.来自样品的信号经过会聚透镜收集后进入Jobin-Yvon iHR320 单色仪,并经单色仪分光后由热电制冷的Synapse CCD 探测器进行探测.

3 结果和讨论

图2 为注入电流为5 µA 时一个基于InGaN/GaN 多量子阱结构的绿光样品(SG1)和蓝光样品(SB)的EL 峰位能量和线宽的温度依赖性.由图2可见,绿光样品SG1的峰位能量和线宽都显示了一个近似的“V 形”(降低-增加)温度依赖行为;相比之下(图2 内插图),蓝光样品SB的峰位能量则显示了一个“S 形”(降低-增加-降低)温度依赖行为,同时它的线宽显示了一个近似的“W 形”(降低-增加-降低-增加)行为.这两个样品的上述行为均可归因于InGaN 阱层中组分起伏所诱发的势起伏以及由此产生的载流子复合的局域特征[27,28].然而,相比之下,绿光样品SG1有一个更强的载流子局域效果,这是因为在高温范围内(＞ 200 K)蓝光样品SB所展现的峰位能量随温度降低的行为近似地遵从自由载流子的一般热化过程(即遵从Vashni方程Eg(T)=Eg(0 K)-αT2/(T+β) ,其中Eg(T)和Eg(0 K) 分别表示温度为T和0 K 时样品的禁带宽度,α和β为常数)[21,22],而绿光样品的峰位能量却随着温度的增加而单调增加.这反映了在上述的高温范围内蓝光样品SB辐射过程是以自由载流子的一般热化为主,而绿光样品SG1则仍以局域载流子的热化为主.因此,与绿光样品SG1相比,蓝光样品SB在300 K 时的辐射能量应当更接近其真实的光学带隙.换言之,解局域(delocalized)自由载流子(即自由载流子)的支配性复合发光是测量其光学带隙不可缺少的前提条件.而对于深局域绿光样品,可适当提高注入电流来降低其局域效应,使其EL 峰位能量在高温范围内遵从Varshni 方程,以满足带隙测量条件.

图2 注入电流为5 µA 时,SG1 的EL 峰位能量和半高全宽(FWHM)的温度依赖性.插图为5 µA 时SB 的EL 峰位能量和FWHM 的温度依赖性Fig.2.Temperature dependence of the EL peak energy and FWHM for SG1 measured at 5 µA.The inset is that for SB measured at 5 µA.

图3 显示了绿光样品SG1的一个姊妹样品(SG2)在不同注入电流下其EL 峰位能量和线宽的温度依赖性.需要说明的是,与绿光样品SG1相比,绿光样品SG2有较低的InGaN 阱层生长温度,因此该阱层具有较高的平均In 含量和较强的局域效果.由图3 可见:在较低的注入电流下(小于0.5 mA),随着温度的增加(大于200 K),EL 峰位能量单调增加;在中等注入电流下(0.5—350.0 mA),随着温度的增加(大于160 K),EL 峰位能量首先以较快的速率降低,然后以较慢的速率降低.这表明在上述测试条件下(即小于350 mA),绿光样品SG2仍然有较强的载流子局域特征.而只有当注入电流等于或大于350 mA 时,其辐射过程才在高温范围内近似地遵从Varshni 方程.

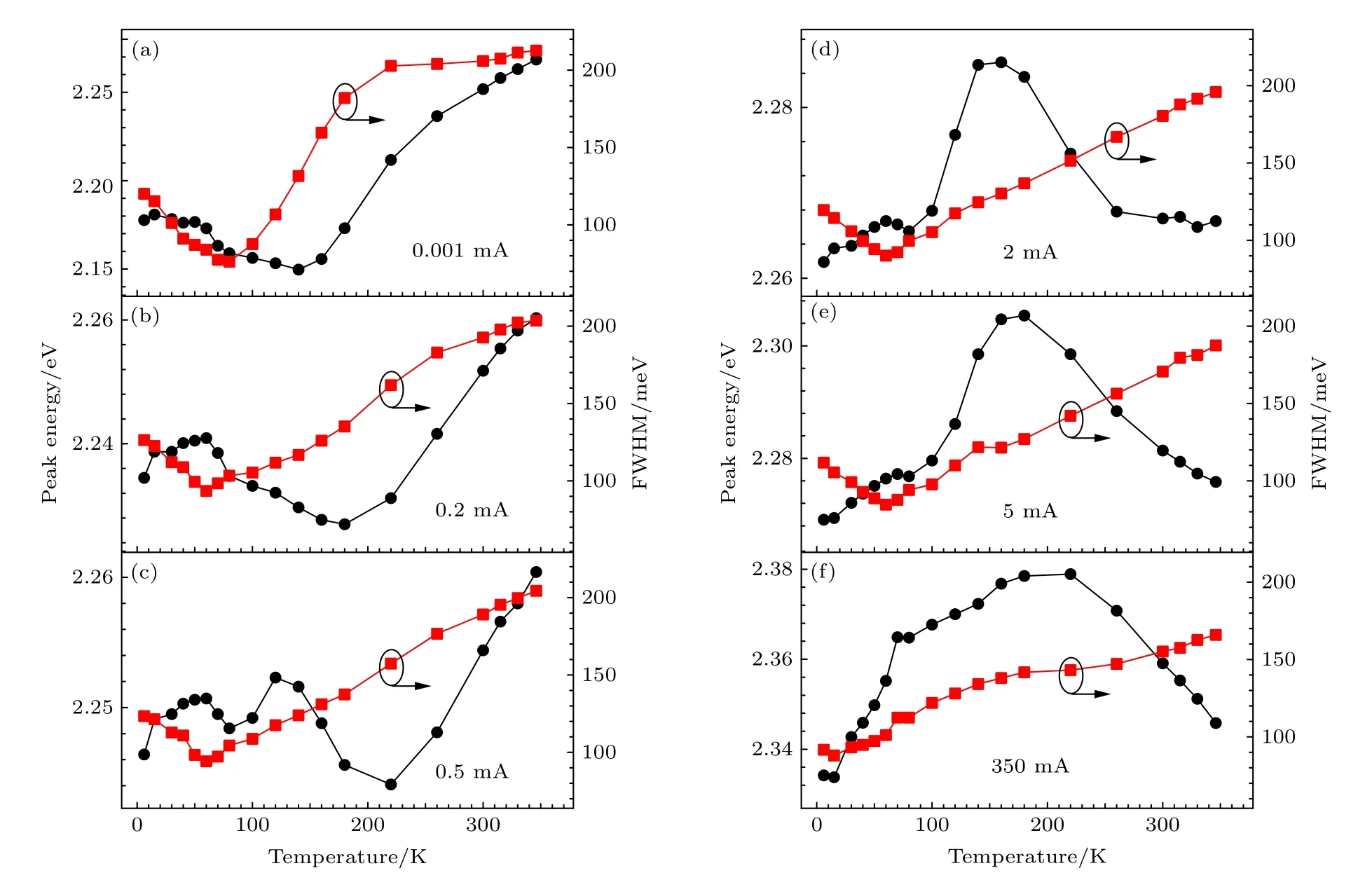
图3 注入电流为0.001 mA (a),0.2 mA (b),0.5 mA (c),2 mA (d),5 mA (e)和350 mA (f)时SG2 的EL 峰位能量和FWHM 的温度依赖性Fig.3.Temperature dependences of the EL peak energy and FWHM for SG2 measured at 0.001 mA (a),0.2 mA (b),0.5 mA(c),2 mA (d),5 mA (e),and 350 mA (f).

图4 显示了蓝光样品SB在不同注入电流下其峰位能量和线宽的温度依赖性.结果显示,在所有的注入电流下,峰位能量-温度曲线在包含300 K在内的高温范围内均遵从Varshni 方程.但是,在不同注入电流下,300 K 所对应的峰位能量却各不相同.一般来说,对于一个特定的结构,在某个固定温度下它的光学带隙应该是一个定数,不会随注入电流的变化而变化.上述结果表明,峰位能量遵从Varshni 方程并非是带隙测量的唯一前提条件,除此之外还需要考虑其他因素的影响.

图4 注入电流为0.01 mA (a),5 mA (b)和200 mA(c)时SB 的EL 峰位能量和FWHM 的温度依赖性(虚线代表Varshni 曲线)Fig.4.Temperature dependences of the EL peak energy and FWHM for SB measured at 0.01 mA (a),5 mA (b),and 200 mA (c).The dashed lines represent Varshni curves.

为了进一步探讨精确测量光学带隙所需要的测试条件,图5 给出了蓝光样品SB在300 K 下其EL 峰位能量的注入电流依赖性.由图5 可见:随着注入电流从0.01 mA 增加到200 mA,峰位能量首先增加,并且在0.02 mA 左右达到最大值,然后降低,并且在2 mA 左右达到最小值;随着注入电流的进一步增加,峰位能量单调增加到200 mA.相应于上述过程,其EL 线宽则表现为首先增加,并且在2 mA 左右达到最大值,然后减小到10 mA.随着注入电流的进一步增加(≥ 10 mA),线宽单调增加到200 mA.上述行为可解释为:随着注入电流的增加(≤ 2 mA),局域态的填充效应首先支配该样品的辐射发光过程(≤ 0.02 mA),然后非辐射复合开始增强并占据支配地位;随着注入电流的进一步增加(≥ 2 mA),非辐射中心逐渐变得饱和,并且QCSE 的屏蔽效应开始支配该样品的辐射发光过程(≤ 10 mA),然后这个屏蔽效应被随后的载流子的高能局域态的填充效应或导带底的填充效应所取代(10—200 mA).也就是说,当注入电流大于10 mA 时,InGaN 阱层中来自组分起伏相关的局域态(尤其是低能局域态)的填充效应、杂质/缺陷相关的非辐射复合以及极化场相关的QCSE的屏蔽效应不再明显,并且来自导带底(也可能包括近带边处高能局域态)的填充效应开始占据支配地位[25,29,30].结合图4 的测量结果(即10 mA 时在目标温度附近峰位能量已完全遵从Varshni 方程),图5 中10 mA 的临界电流值所对应的峰位能量可近似看作是该结构InGaN 阱层的光学带隙.需要指出的是,如果选取的电流远大于10 mA,那么阱层中显著的导带底的填充效应将会使得测量结果(即峰位能量)明显大于实际的带隙宽度.其他目标温度下的带隙宽度测量和上述300 K 目标温度条件下的测量方法类似.应当注意的是,在较高的注入电流(或光激发功率)下,量子阱层可能会发生载流子泄漏(overflow)现象[31-33],但这并不影响对阱层带隙的荧光测量,因为这些泄漏载流子对阱层的荧光辐射没有贡献.此外,在高密度载流子状态下,阱层中有可能还会发生俄歇复合,进而降低发光效率.然而,据我们所知,有关俄歇复合对辐射能量的影响机制的研究却鲜有报道.因此,俄歇复合是否会影响本文所述的带隙判定现在还不清楚,还需要进一步的研究和探讨.但我们猜想,俄歇复合对本文所述的带隙判定方法应该不会有明显的影响,因为俄歇复合是一种非辐射复合,并且一般来说,引起俄歇复合发生时所需要的注入电流(或光激发功率)的阈值要大于消除上述因素(即非辐射复合、局域效应和QCSE)所需要的临界值.

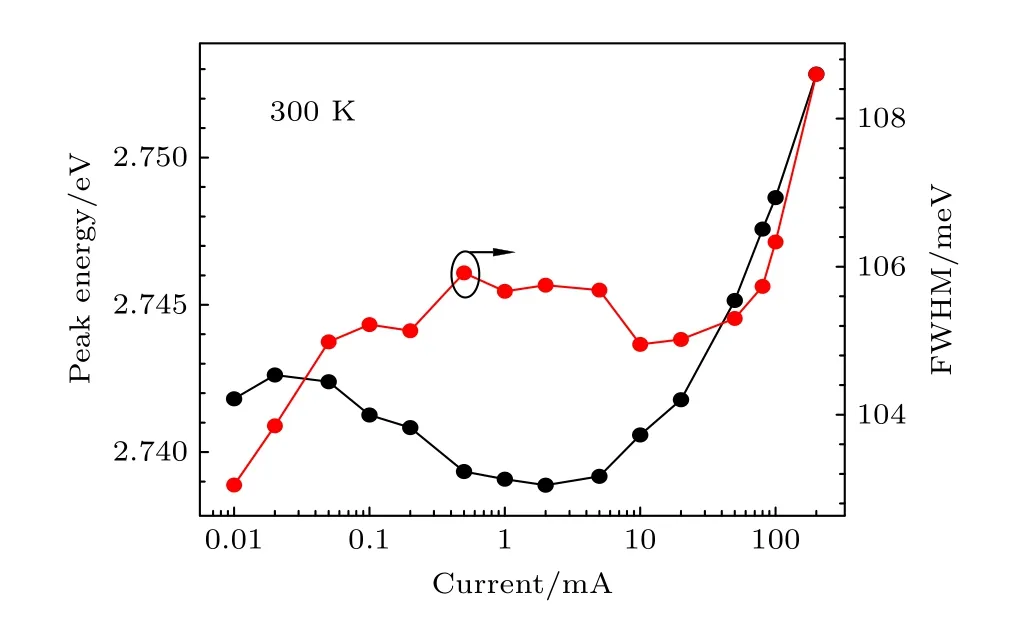
图5 温度为300 K 时SB 的EL 峰位能量和FWHM 的注入电流依赖性Fig.5.EL peak energy and FWHM as a function of injection current for SB at 300 K.

上述带隙测量方法中所包含的两个测量步骤(即不同注入电流下的EL 峰位能量和线宽的温度依赖性;目标温度下的EL 峰位能量和线宽的注入电流依赖性)缺一不可,具体原因如下:1)如果只测量某个注入电流下的峰位能量和线宽的温度依赖性,则只能据此判断在该注入电流下目标温度附近的辐射过程是否符合Varshni 方程,而难以判断在该注入电流和目标温度下QCSE 是否已经消失[26,27];2)如果只测量目标温度下的峰位能量和线宽的注入电流依赖性,则只能据此大致确定非辐射中心和局域(尤其是低能局域)中心达到饱和以及QCSE 被屏蔽时所需要的临界注入电流的大小,而难以判断在该注入电流和目标温度下来自高能局域中心的辐射是否仍然显著(即是否已经完全被导带底的填充效应所取代)[27].需要注意的是,由于样品结构的不同或者是测试条件的不同,当注入电流增加时,其辐射过程有时会表现为载流子的低能局域态的填充效应[30],有时会表现为从高能局域态到低能局域态的载流子散射效应[34,35],有时会表现为非辐射复合、QCSE 的屏蔽效应、高能局域态的填充效应以及导带底的填充效应,甚至有时这些效应会同时出现在某一激发过程中的不同激发阶段,并且它们出现的次序也不尽相同[23,25,35].但只要遵从上述的两个测量步骤,基本上就能够消除上述因素的干扰,判断出导带底的填充效应开始占据支配地位时的临界注入电流的大小.在此临界注入电流下,如果目标温度附近的峰位能量遵从Varshni方程,那么目标温度所对应的峰位能量即可近似地被看作是光学带隙能量.此外,尽管EL 方法和PL方法都可被用来测量带隙宽度,但相比之下,PL方法应该有更高的测量精度,因为该方法避免了外加电场对测量过程的干扰.EL 方法在测量中所施加的外部电场会额外增强有源区能带的倾斜程度,并由此导致QCSE 的进一步增强,从而导致阱层的有效禁带宽度降低.

4 结论

本研究选取了3 个由金属有机化学气相沉积方法外延生长的InGaN/GaN 多量子阱LED 的EL 数据作为分析对象,探讨了荧光法测定极化场中多元合金在某个目标温度下的光学带隙所需要满足的测试条件.对于这些InGaN/GaN 多量子阱结构,由于有源区中存在着杂质/缺陷、组分起伏以及界面晶格失配等现象,其辐射发光过程在不同程度上会受到非辐射复合、局域势起伏以及QCSE的影响,从而导致光学带隙的测量结果会出现不同程度的偏差.为了获得目标温度下较为精确的光学带隙,就必须优化测试条件,例如,在不同注入电流下测量荧光谱的温度依赖性以及在目标温度下测量荧光谱的注入电流依赖性.通过综合这些测量结果并选取合适的注入电流,来降低甚至消除非辐射复合、局域效应以及QCSE 所带来的不利影响.在这样的测试条件下,目标温度所对应的辐射峰位能量便可近似地认为是目标结构的带隙宽度.一般来说,由于上述因素(即非辐射中心、局域中心和极化电场)会不同程度地存在于目标半导体(包括元素半导体、二元或多元合金)或其相关异质结构中,因此该测试条件可适用于常见半导体(包括直接带隙和间接带隙材料)的带隙测量,尽管样品结构的多样性会导致其具有不同的光学特征.期待本研究方法或研究思路能对相关半导体材料的带隙测量有所帮助.