基于特征价格模型的轨道交通对沿线住宅价格影响研究——以长沙轨道交通1号线为例

唐钱龙，胡婉萱

(1. 中南大学土木工程学院，湖南 长沙 410075；2. 江西交通职业技术学院，江西 南昌 330013；3. 江西财经大学法学院，江西 南昌 330013)

特征价格模型是国内外学者运用最为广泛的研究模型，李菁等[1]针对武汉地区589 个商品房小区的房价数据，通过引入影响因子，观察影响因子的进入或剔除导致房价的变化；都沁军等[2]通过研究石家庄地铁1号线折射出土地增值效应与地铁站点距离的相关关系；汪静雪[3]从时间和空间2 个维度考虑住宅价格在地铁建设从开工−施工−竣工−运营阶段的不同影响。李嘉[4]从空间的角度分析武汉地铁站点对房价的影响，并测算地铁站点内的不同辐射距离对房价的影响程度。路刚[5]针对北京地铁9 号线辐射1 000 m 区域内对房价的影响因素进行研究，包括其外部性因素与建筑内部性因素，得出相似结论。鉴于此，基于特征价格模型，提取合适的特征变量，通过模型检验、描述性统计、半对数回归形式对城市轨道交通的外部经济性进行量化研究，得出相关结论。“十四五”规划和2035 年远景目标中指出，建设交通强国是实现各种运输方式一体化综合发展，提高网络效应和运营效率的重要环节。城市化进程的深入、经济的增长以及人口数量的增长都对中国城市公共交通提出了更高的要求。因为轨道交通有运输容量大、安全、出事故概率低、速度快等优点，使轨道交通成为各国解决城市交通问题的首选。迄今为止，中国地铁已历经五六十年，地铁这一公共交通受到越来越多国家的青睐。近年来，地铁不仅在一线城市站稳脚跟，很多二三线城市也看到了地铁得天独厚的优势，从图1可以看出，中国近十年来的轨道交通发展迅速，光从运输里程上看，中国地铁保持了稳定增长，从2010 年的1 471 km 发展到2018年的5 295 km，足足翻了5番。随着地铁为人们所熟知，地铁市场的红利值得期待。

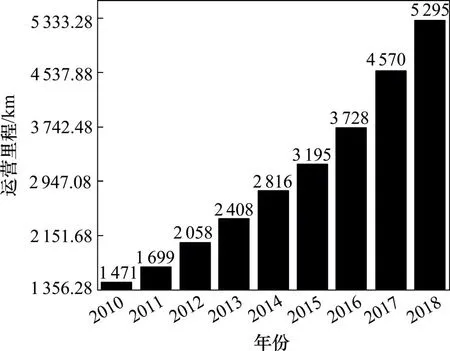
图1 中国轨道交通运营里程Fig.1 Operational mileage chart of rail transit in China

由图2 可知，自2010 年起，轨道交通客运量一直保持着稳定增长，直至2018 年达到2 127 659万人次，相对于公交，地铁以其优势迅速占据了市场。地铁近年来深入大众视野，地铁的作用已经扩展到各个行业各个角落，地铁的建设与运营不管是对于房地产业、零售业以及极其重视人流的快销产业都是一个重大商机。如何科学量化轨道交通的经济效益，是各大企业以及当代学者们不断探索的课题之一。住宅的价格与地铁有很强的相关性，因此，地铁无疑成为了消费者在选择住宅时考虑的一个重要因素，如何衡量地铁对周边房价的影响程度成为消费者以及房地产商估价不可避免要考虑的问题。

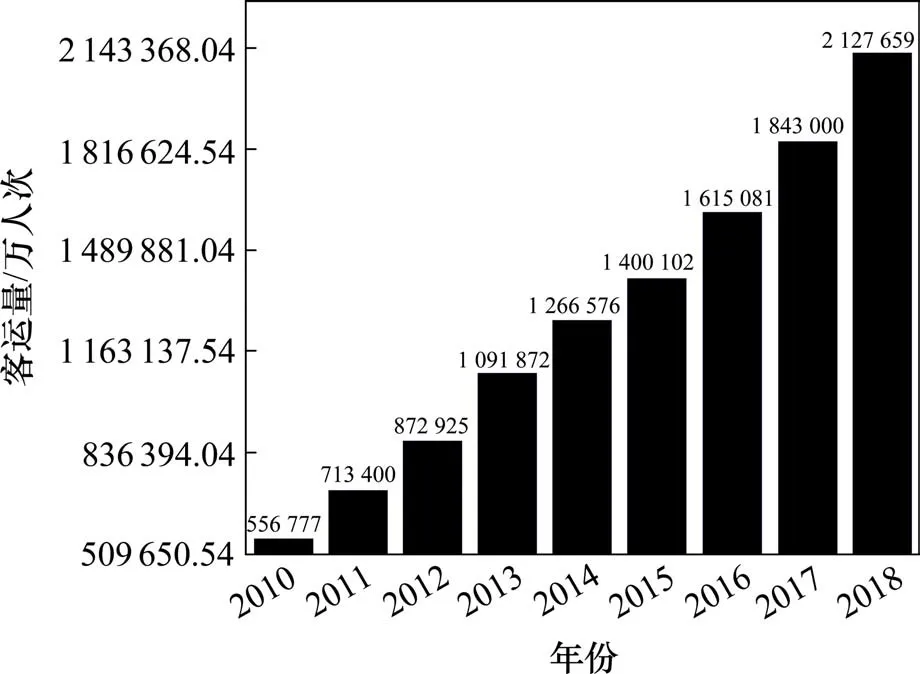
图2 轨道交通客运量Fig.2 Rail transit passenger volume

1 长沙市的基本状况

1.1 宏观经济发展状况

房价的影响因素往往受到宏观与微观因素的影响，尤其是房地产行业作为国家支柱性行业，容易受到国家宏观政策的影响。从数据上来看，长沙市近年来经济发展势头良好，有利于房地产行业的发展。2019 年全市实现地区生产总值达11 574 亿元，人均地区生产总值为13.79 万元，长沙市2010～2019 年地区生产总值如图3 所示。长沙市的GDP 总量和人均GDP 分别实现持久性增长，人均GDP 达到13.79 万元，如图4 所示。长沙市良好的城市经济发展势头给长沙市房地产行业的发展创造了有利的条件。

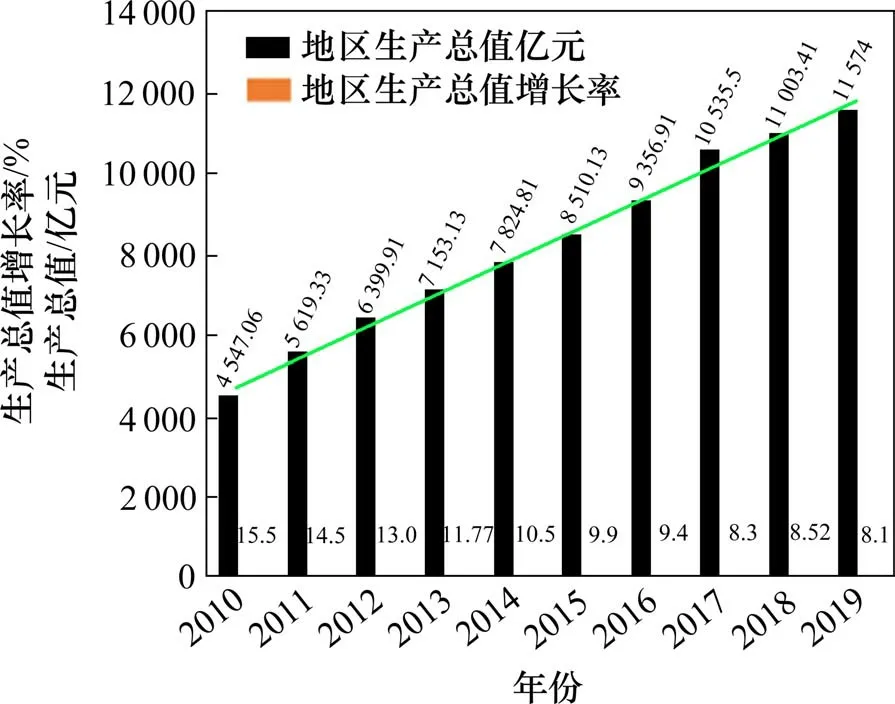
图3 长沙市地区生产总值变化情况Fig.3 Changes of GNP in Changsha

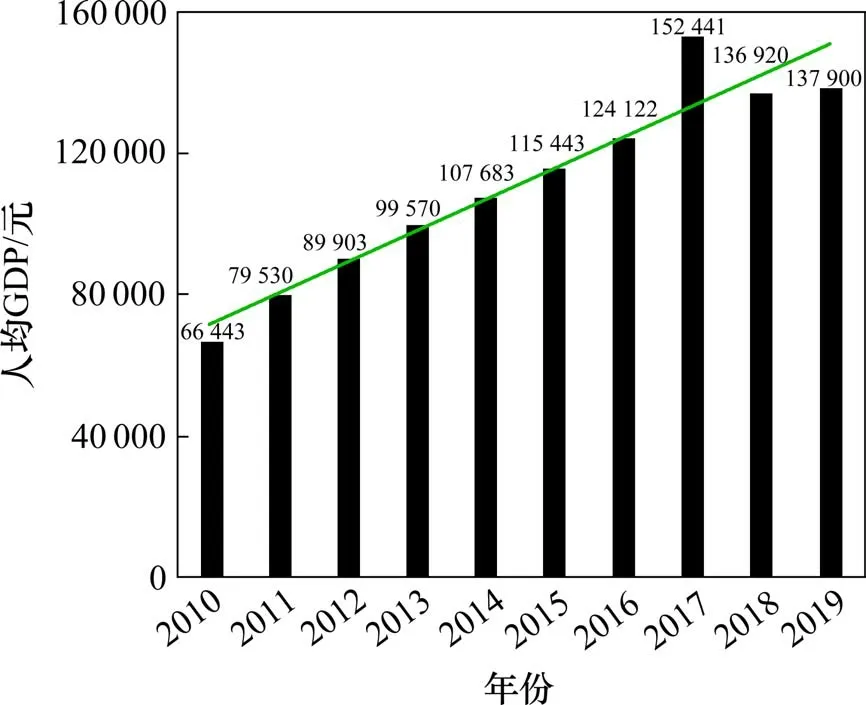
图4 长沙市人均GDP变化情况Fig.4 Change of per capita GDP in Changsha

长沙市近十年的全社会固定资产额保持稳定增长，2010～2019 年呈现增长趋势；房地产投资额在2010～2014 年的5 年间保持稳定增长，2015年有所下降，在2016 年～2019 年恢复增长趋势，如图5所示。

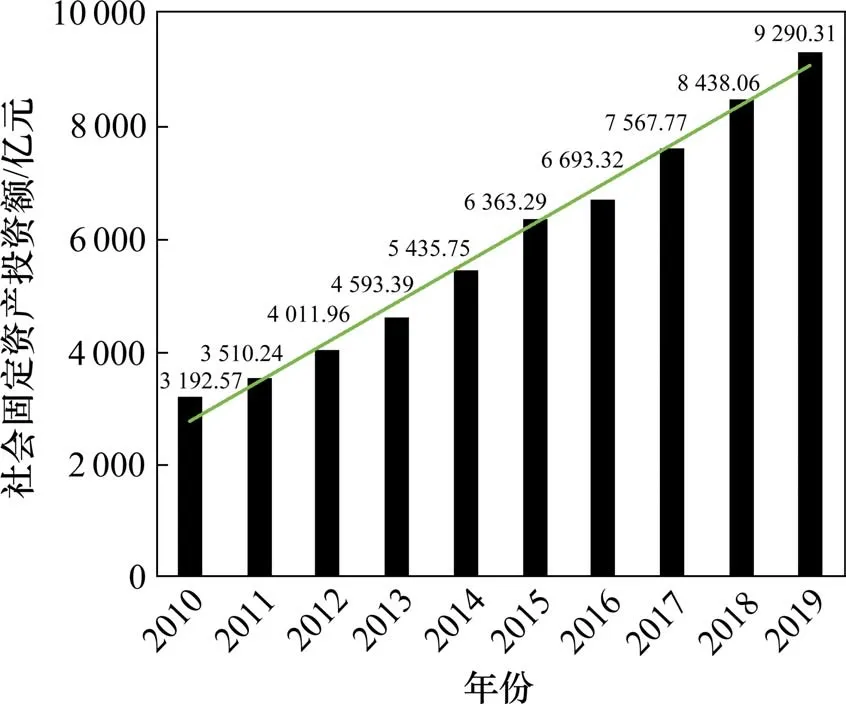
图5 长沙市社会固定资产投资额Fig.5 Social fixed assets investment in Changsha

1.2 房地产市场状况

长沙市近十年以来的土地供应量有着较大的起伏，在2010～2013 年土地供应量保持稳定，上下起伏不大，从2014～2019 年土地供应量大幅波动，并呈现出一升一降的趋势；土地出让金则在2014～2019 年保持着平稳增长的趋势，如图6所示。

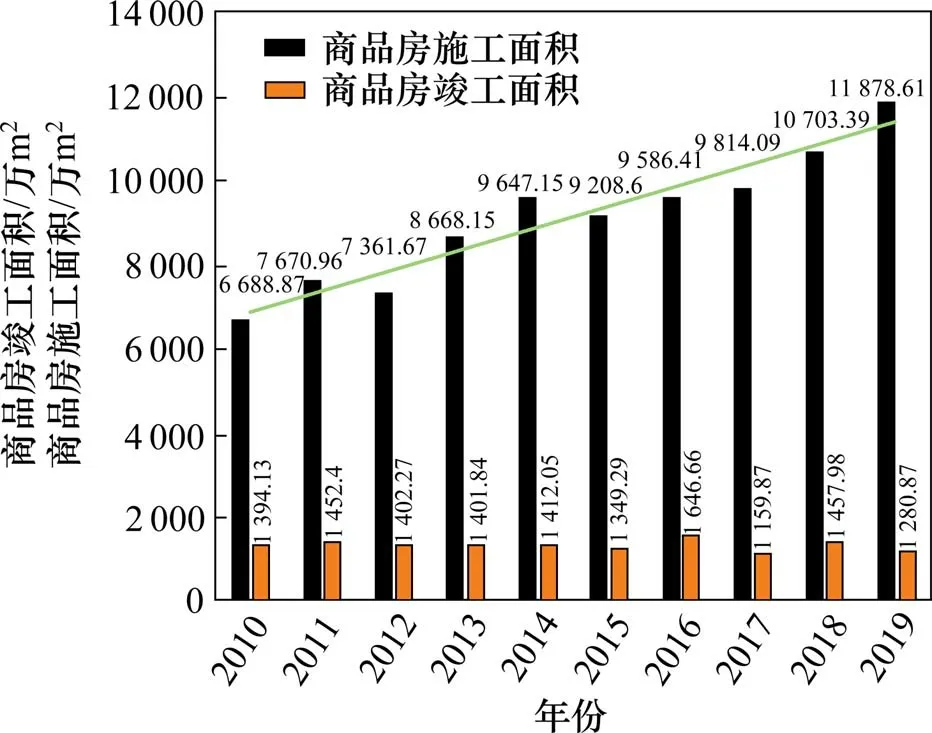
图6 长沙市土地出让金、土地供应面积总量变化情况Fig.6 Changes of land transfer fees and total land supply area in Changsha

长沙市2010～2019 年房地产施工面积起伏较大，在2012～2014 年保持稳定增长，在2015～2016 年稍有回落的趋势，但在2017～2019 年恢复增长，并在2019 年达到最大值至11 878.61 万m2；长沙市近十年的房地产竣工面积保持了幅度较小的增长，最大值出现在2016 年，为1 646.66 万m2，如图7所示。

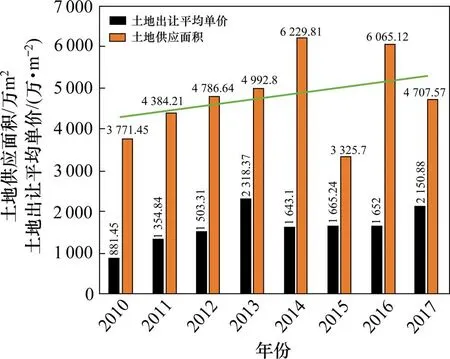
图7 长沙市房地产施工面积和竣工面积情况Fig.7 Construction area and completed area of real estate in Changsha

长沙市商品住宅成交价格在2010～2015 年上下起伏不大，保持循环起落，但从2016 年开始，商品住宅平均销售价格出现大幅上涨，并在2016～2019年保持稳定增长，在2019年达到了8 657元/m2，同2018年相比，上涨了5.35%，如图8所示。

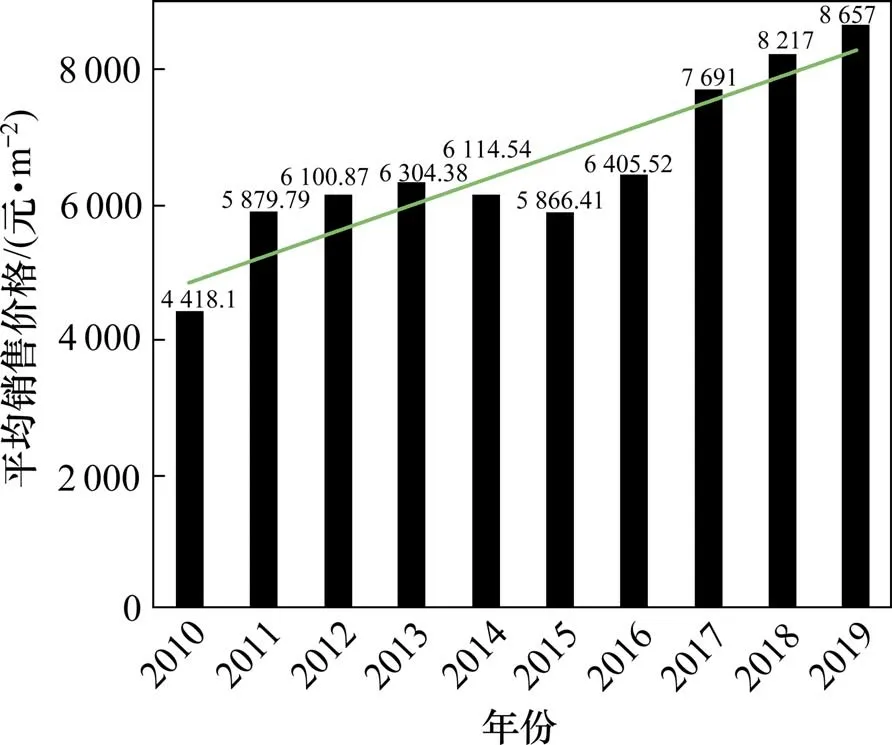
图8 长沙市商品住宅平均销售价格Fig.8 Average sales price of commercial residential buildings in Changsha

1.3 轨道交通发展现状

根据长沙市城市规划局官方发布的文件来看，迄今为止，长沙市已经有5 条地铁线路在运营当中，运营里程达到了161.2 km，在全国排名第15位。2020 年长沙市开通了3 号线1 期、5 号线1 期，根据相关数据统计，长沙市地铁日总流量已经突破了历史最高点，达到了157.4 万乘次。根据相关数据显示，长沙市近年在建轨道交通线路长度起伏较大，但总体为上升趋势，尤其是在2014～2017 年保持了稳定增长的趋势，并在2017 年达到近十年来长沙在建轨道线路长度峰值至140.58 km；长沙轨道交通建设换乘站数在近十年内也取得了可人的进步，在2018和2019年分别建成了71个站点，将站点覆盖整个长沙市，便利人们的工作与生活。

2010 年12 月长沙地铁1 号线正式开工建设，向北始于开福区政府站，沿黄兴路、芙蓉路通过20座车站一直延伸到尚双塘站，从2010年12月26日开工建设，历时5 年半建成，于2016 年6 月28日正式开通试运营。

2 研究设计

2.1 特征价格模型

2.1.1 特征价格模型的内涵

特征价格模型在研究对象满足具备不同特征这一条件的基础上，进而研究对象的价格与其不同特征之间的某种特殊关系，最终获得相关结论[6]。往往一件商品是由一个包含众多特征的集合构成，因此，通常来说，商品价格表现为特征的函数和随机干扰值之和[7]。特征价格模型在引入被解释变量、解释变量、虚拟变量进行函数关系分析领域中，通过与计量经济学的结合，具有不可忽视的意义。尤其是在房地产价格作为被解释变量分析其影响因素函数关系时，特征价格模型是一个绝佳选择。

特征价格理论提出，一般来说异质产品极具有普通商品的共性，又具有与之不同的个性[8]。产品作为这些特别属性的集合，在出售时，既可以是价值的估价，也应该是产品的特征价格的估价，可以衡量市场对于其的需求[9]。特征价格模型不仅应用于对商品的策划估价之中，更多的是进行多元回归线性分析，发现多种影响因素对被解释变量的实证影响，在满足一定条件情况下时，可以固化某个或多个因素对被解释变量的影响，单单聚焦于某个因素的线性影响作用[10]。

2.1.2 特征价格模型方程

特征价格方程，是以特征变量的变化引起价格的变化为核心[11]。在本文研究当中，价格应该是房价，而影响房价的各种特征则包括容积率、建筑面积、楼层、周边配套设施完善程度等。由于特征价格模型的方程式不单单是线性形式，故在选取方程进行分析时，首先需要选择拟合度较好的方程式作为模型分析的函数形式，以保证结论的精确性与合理性。

通常，特征价格模型的函数形式主要有以下3种[12]：

第1种是线性形式，是在进行线性回归分析中最为浅显简单的基本函数形式[13]，每当特征变量发生一单位变化引起的房价发生的价格变化情况；

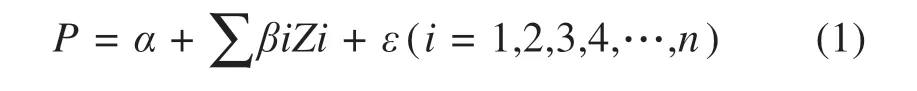
式中：P表示houseprice；Zi表示各特征变量；βi为第i个特征变量的系数；α代表常数；ε为随机误差项。

第2种是对数形式，由于研究对象以及变量数值尺度的限制，也是为了研究自变量与因变量之间的弹性关系，采取对数形式利于缩小数值尺度[14]，保证准确性，表示的是自变量的单位百分比变化所引起的房价的百分比增减；

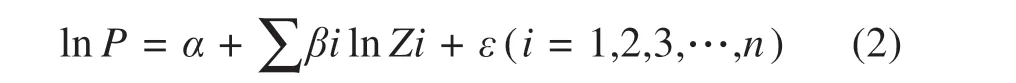
第3 种是半对数形式，即等式左边(被解释变量)采用对数形式，特征变量采用普通形式，该形式相对于对数形式的优势在于可以弥补对数形式等量右边不能去零的缺陷，表示自变量的每一单位变化引起的房价的单位百分比增减。

为了保证模型检验拟合度合理性，在2.4.1对3种函数形式进行模型检验，选择其中拟合度较高的模型进行数据实证分析。

2.2 研究对象、时期确定及样本选择

本文研究目的在于量化长沙轨道交通1号线对周边住宅价格的影响程度，此次研究涉及到2个主体—长沙轨道交通1号线和沿线住宅价格。从论文的时效性来看，长沙轨道交通1 号线自2010 年开工建设，2016 年开始通车运营，到2019 年，这条地铁线路已经是一条非常成熟的交通要道。选择这条线路作为研究对象，主要是为了研究1号线自开工建设始直至运营等整个过程对住宅价格的影响，体现时效性与全面性。在选取住宅样本价格数据的时候，注重全面化，尽可能全面地搜集2009 至2019 年近10 年的住宅样本数据，以保证论文研究所选取的房地产交易数据在年份上具有时效性和全面性。

本文搜集了长沙地铁1 号线各站点1 600 m 内的数据，所收集的样本楼盘主要分布在涂家冲站、铁道学院站、省政府站、中信广场站、侯家塘站、南湖路站、文昌阁站、桂花坪站。

2.3 数据来源

本文所有的研究数据均利用网络技术手段获得，关于轨道交通本身的数据来自于百度百科，关于宏观经济数据来自于本校针对学生开放的宏观经济与房地产数据库。至于本文的住宅样本数据(房屋成交价)则来自于房产中介公司，例如贝壳找房、房天下信息网、安居客、房途网。模型构建、空间影响研究的数据收集时间大体在2021年1月份完成。关于自变量中的楼盘类型(高层、中高层、低层)、房龄、容积率、绿化率、物业费、楼层等均从房天下网站的挂牌价格信息中获取；住宅样本至市中心、医院、学校的距离等关于周边设施情况的都由百度地图测量获得。

2.4 模型构建与变量选择

2.4.1 模型构建

本文将设定的变量(表1)代入住宅价格模型的线性方程、对数方程形式以及方程半对数形式，用SPSS20.0 分别估算3 种线性模型的拟合度测算，并决定在后续实证分析中采用何种形式。通过表1可以得出，模型的R方为0.638，调整后的R方为0.606，说明本模型的全体自变量总体上对应变量Inhouseprice 的影响限制性为60.6%，且D-W值为1.900，接近于2，该数据显示模型拟合度、误差项独立性良好。

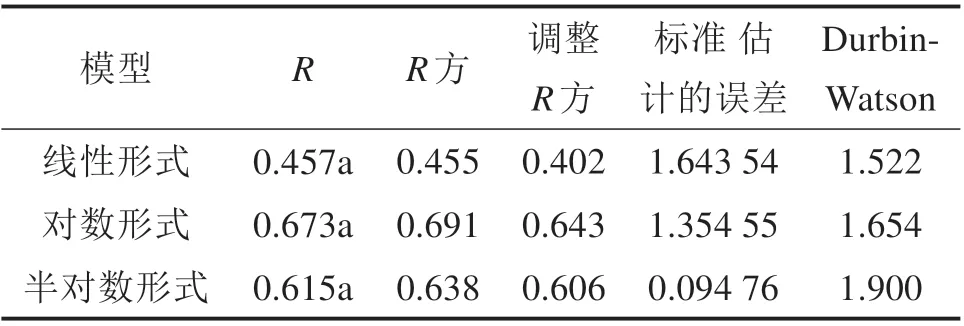
表1 模型汇总Table 1 Model summary

2.4.2 变量选择

在构建一个数据模型时，第1步就是要确定解释变量与被解释变量，变量的选择对于数据结果准确性与科学性都非常重要。影响住宅价格的因素很多，不单单是地铁交通这一个，包括建筑物自身的特征还有周围的因素。根据房价的影响因素分析，分为区位、邻里和结构3 类[15]，故本文选取特征变量时也按照该分类进行选择，其中区位特征变量根据楼盘距离地铁站点的距离分为Met‐ro0，Metro1 和Metro2；邻里特征变量主要考虑的是楼盘附近的基础配套设施虚拟变量，如super‐store，bus，hospital，school 和park 等；结构特征变量指的是楼盘本身结构因素，如建筑类型、建筑面积、容积率等变量。由于时间与精力有限，本文选择了在地铁线周边101个楼盘作为此次调查的样本数据，数据来源均来自于安居客、链接网、房途网等房地产网站，根据百度地图中的测距功能选取样本。具体变量汇总见表2。

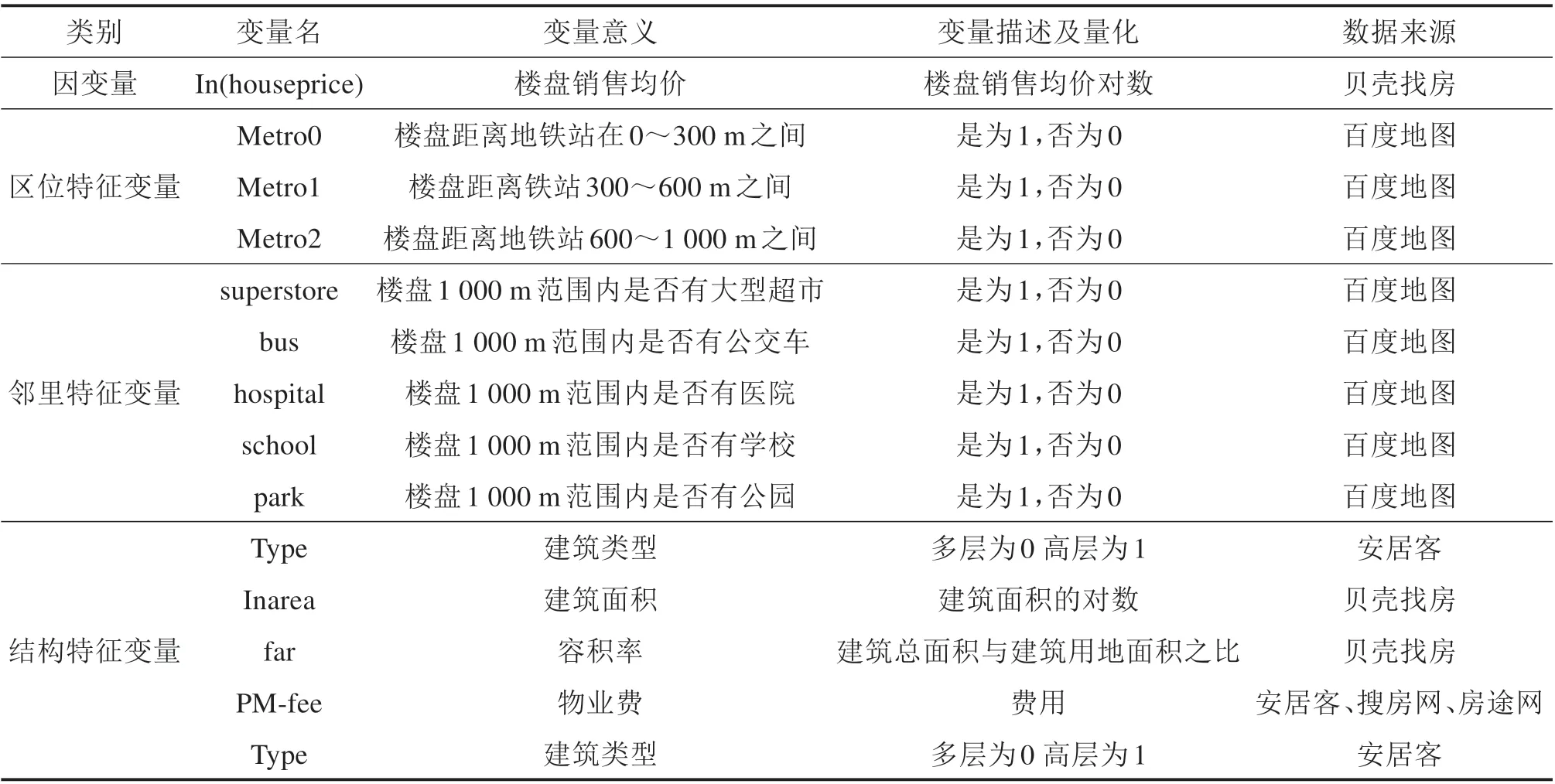
表2 各变量汇总表Table 2 Summary table of variables

3 实证结果及分析

3.1 描述性统计

利用SPSS工具获得描述性统计，见表3。

表3 变量描述性统计Table 3 Descriptive statistical table of variables

从表3 中可以看出，变量Lnhouseprice 代表的是1号线周边0～1 600 m 范围住宅的销售均价的对数，变量Metro0 表示的是0～300 m 以内的住宅区域范围；Metro1 表示的是300～600 m 以内的住宅区域范围；Metro2 表示的是600～1 000 m 以内的住宅区域范围；其他的是距离站点1 000 m 以外的住宅区域范围。

3.2 模型检验

表4为回归方程显著性检验结果，可得被解释变量的总平方和SST 为1.362，根据模型原理，在进行模型显著性检验时，模型对应的概率P越趋近于0，则证明该模型变量之间存在合理的线性关系[16]，从表4 可知，回归方程显著性检验的F 统计量的观测值为6.164，选择半对数线性模型具备合理性。

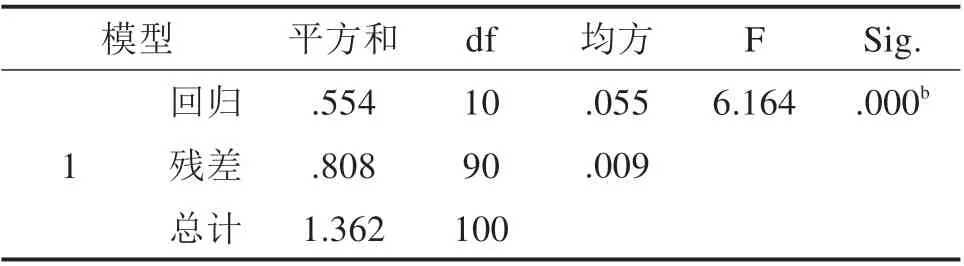
表4 AnovaTable 4 Anova

从图9 可以看出，当In(houseprice)作为被解释变量时，回归标准化残差总体分布在(−2.2)之间，近似呈正态分布，说明本文所构建的模型满足方差齐次性的假设[17]。

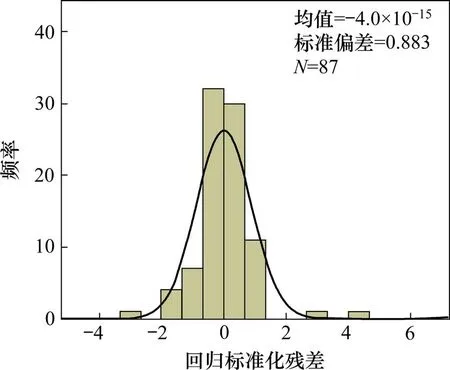
图9 回归标准化残差图Fig.9 Residuals of regression standardization

3.3 线性回归

由表5 可知，由于容积率变量(far)Sig.值0.067大于显著性水平0.05，则接受原假设，回归系数为0，排除此变量，将回归系数代入函数公式分析如下。

1) 空间影响效应

通过对地铁与站点距离对房价的影响进行分析，得到表5的回归系数，分析可以发现地铁站对沿线住宅价格的影响程度与房屋与地铁站点的距离密切相关，函数方程如下：

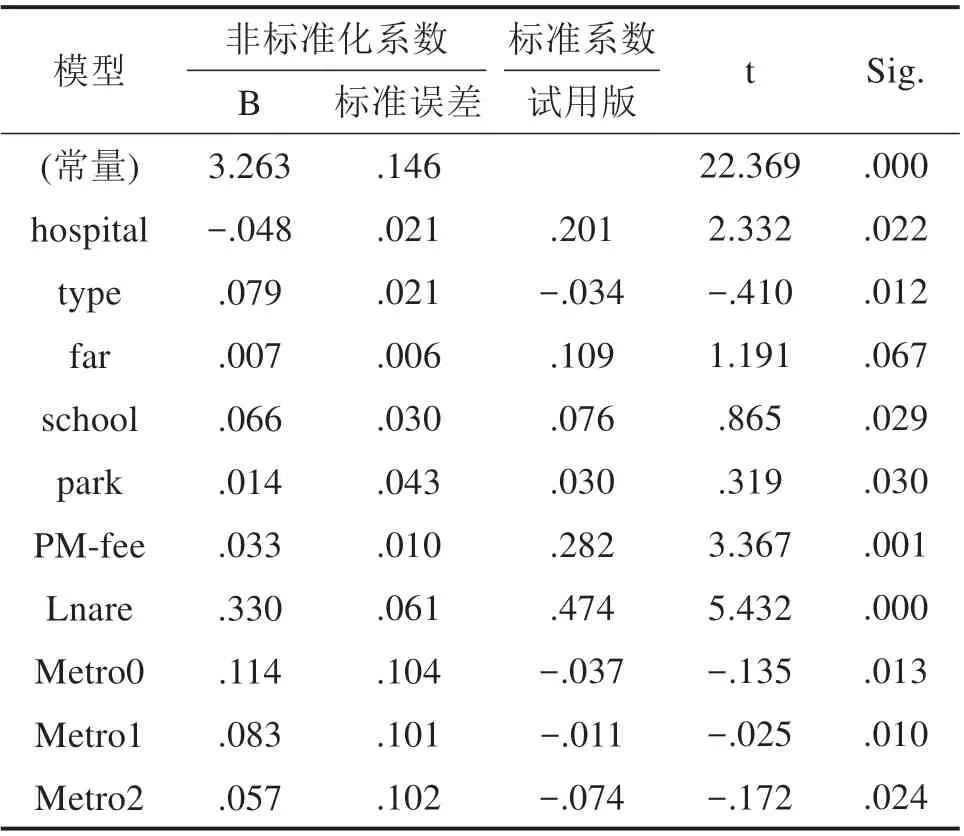
表5 系数aTable 5 Coefficient

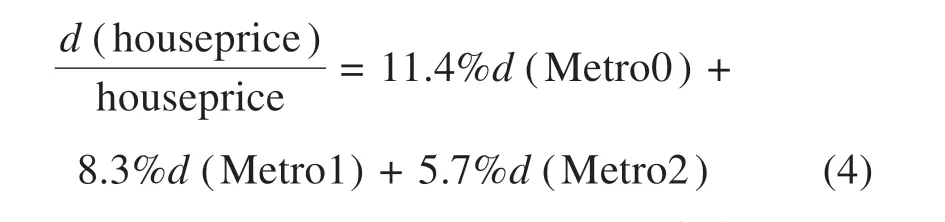
由此可得，当地铁站点与住宅距离变大时，回归系数呈现不断减小的趋势，最终得出结论：假设只考虑地铁这一个因素会影响住宅价格，当住宅位于距离站点0～300 m 时，其房价一般要比其他住宅高11.4%；当住宅位于距离站点300～600 m 的区域范围内时，其房价一般要比其他住宅高8.3%；当住宅位于距离站点600～1 000 m 的区域范围时，其房价一般要比其他住宅高5.7%；当住宅位于距离站点1 000 m 或者1 000 m 以外的区域范围时，地铁距离站点的距离对房价的影响一般，基本上可以忽略不计。

2) 其他因素对房价的影响，回归系数方程如下：

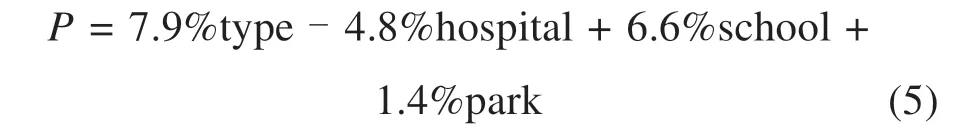
地铁的建设只是房价的影响因素之一，房地产本身因素以及周边配套设施完善程度也对房价有着重要的影响[18]，通过将楼层、容积率、周边设施(医院、公园)作为特征变量分析得到的回归系数可以得出：高层房屋要比普通房屋的价格高7.9%；房屋周边医院的配套与房价在一定条件下呈负相关，这与中国的风俗习惯有关；学校的配套会对房价产生6.6%的正相关影响；房屋公园的配套陈设对房价有着1.4%的正相关影响，这与人们对健康生活的追求有关。

4 结论

1)通过将长沙轨道交通1 号线作为研究对象，在分析长沙市宏观经济与住宅市场、交通建设现状的基础上，选取合适的特征变量，分析研究样本的价格数据和特征变量数据，最终选取了14 个特征变量，并成功建立长沙地铁1 号线的数据模型。

2) 通过研究地铁对周边房价的空间效应，在假设其他因素对房价没有影响，只考虑地铁这一个因素时，研究发现，住宅价格和住宅与地铁站点之间的距离呈负相关关系，通常住宅越接近地铁站点，它的价格也相对较高；反之可推，但这一影响也在一定范围内才成立，在住宅距离站点1 000 m 以外时，地铁这一因素对房地产价格产生的影响基本上可以忽略不计。

3) 通过以房屋成交价作为参照物，并对影响房价的因素进行变量设置，进一步量化轨道交通对效应对象房价的外部性经济效益，相对科学地探究了长沙市轨道交通1号线外部经济性。