卷积自编码器融合核近似技术的异常检测模型
2022-03-30武玉坤陈沅涛
武玉坤,李 伟,陈沅涛
(1.浙江邮电职业技术学院,浙江 绍兴 312366; 2.浙江工业大学 计算机科学与技术学院,杭州 310023; 3.长沙理工大学 计算机与通信工程学院,长沙 410114)
0 引言
异常检测是模式识别领域中众所周知的问题, 在正常或预期模式已知的情况下,分类器要识别的异常模式都是在训练集中稀缺或不存在的模式数据[1]。它可以定义为一类分类(OCC,one-class classification)问题,图像中异常行为的分类一直是一个非常有趣的话题,近年来许多研究都集中在检测异常图像和自动视频监控中的事件[2-3]。
通常,异常检测算法是通过学习数据的特征表示,然后把那些远离这个框架模型的数据视为异常;具有大量实例(训练集)的已知类别(正常模式)被称为正类或目标类。大量方法已被广泛用于异常检测问题。例如基于邻居的模型、基于统计的模型和基于深度学习的模型。Xu 和 Ricci使用单分类支持向量机来预测视频中的异常帧[4]。Kim和Grauman设计了一种用于检测异常活动的单类分类方法,称为时空马尔可夫随机场模型[5]。在文献[6]中,为OCC学习了一个概率模型,分类器是无监督的,不需要标记训练数据。在文献[7]中,训练无监督的深度信念网络(DBN,deep belief network)在相对低维空间中提取一组特征,并用DBN学习的特征训练一类分类器。一般来说,一类分类器对于大型和高维数据集中的决策表面建模效率低下,但是通过将分类器与 DBN 相结合,可以减少冗余特征并提高OCC 的性能。尽管在过去几年异常检测取得了丰硕的进展,但随着数据维度的增长,异常检测就越困难,原因在于任何一个异常样本都可能是一个罕见的实例,被观察到的概率也就越低。在没有人工监督的情况下对多维或高维数据进行稳健的异常检测仍然是一项具有挑战性的任务。因此需要有效的方法来检测大规模高维数据中的异常,并要对不同级别的数据噪声具有很强的鲁棒性。解决该问题广泛采用的方案是降低输入的维数,然后在相应的低维空间中进行检测异常。特征降维的方法有很多,比如主成分分析(PCA,principal component analysis)、核PCA[8]、自编码器(AE,auto-encoder)、非负矩阵分解(NMF, non-negative matrix factorization)、遗传编程、DBN等降维方法。其中,PCA和AE是两种常用的方法。基于PCA的降维方法保留特征值较大的数据信息,丢弃数据信息中具有较小的特征值。AE 是一种基于深度学习的数据降维方法,虽然基于 AE 的降维方法有更多的计算成本,但它已被证明在异常检测中进行特征降维非常成功。深度学习模型已经在图像和视频的监督分类中实现了最优的目标识别性能;之所以有如此高的性能的主要是因为他们可以自动提取特征,并具有卓越的图像表示判别能力。文献[9]中堆叠降噪自动编码器 (SDAE,stacked denoising auto-encoders) 仅使用正类进行训练单类分类器取得了良好的性能。然而,当直接应用于 OCC 问题时,SDAE 可能效率低下,因为自编码器重构层的特征空间映射可能是稀疏的,它不能保证重构层中数据的紧凑表示,在训练过程中,SDAE 的重构层是最小化所有实例的重构误差,而不是试图在特征空间中实现紧凑表示,这个问题阻碍了正类与负类的界定并且减弱了分类性能。
OCSVM是广泛使用的有效用于识别异常的无监督技术。但是OCSVM 在复杂的高维数据集上的性能不是最优的,所以很多文献已经提出了使用特征选择和特征提取方法来处理复杂的高维数据,以便与OCSVM相结合来实现异常检测。在深度学习取得前所未有的成功之后,许多结合使用深度特征提取学习和OCSVM的混合模型已经出现。使用自动编码器作为特征提取器,其中隐藏层表示作为传统异常检测算法(如OCSVM)的输入。由于混合模型使用自动编码器提取深度特征,然后将其提供给单独的异常检测方法,它们无法影响隐藏层中的表征学习。从某种意义上说,特征学习与异常检测任务无关,并且不是为异常检测而定制的。也就是说深度学习的表示学习与OCSVM的异常检测是解耦的,不能实现端到端的学习。另外一个限制是由于OCSVM是一种核学习方法,常用的核函数是高斯核函数,由于核矩阵(Gram)的计算,其计算复杂度随样本量的增加呈平方关系增长。针对此限制的解决方案是采用核近似方法,常用的核近似方法有Nystrom方法[10]与随机傅里叶核近似方法(RFF,random fourier features)[11]。Nystrom方法是得到核矩阵的一个低秩矩阵;随机傅里叶核近似方法是使用随机特征映射显式地将数据映射到一个欧氏内积空间。在平移不变核的情况下,可以使用随机傅里叶特征来设计大规模的核机器学习方法。在文献[11]中,作者提出了利用随机特征来逼近核的方法,而不是使用隐式特征映射。其思想是使用随机特征映射明确地将数据映射到一个欧氏内积空间,就可以使用欧氏内积来进行核近似。Huang等[12]表明,在语音识别中,用随机傅里叶特征进行核近似,浅层核机器学习与深度学习的性能相匹配,同时具有较高的计算效率。
随着当前大数据时代的到来,各种数据集规模越来越大,未知的异常类型越来越多样化,异常检测模型的准确性、鲁棒性以及高效性仍是首要考虑的因素。本文提出了基于深度卷积自编码器与核近似单分类支持向量机相结合的端到端的图像异常检测模型,深度卷积自编码器主要用于表示学习以及降维,深度自编码器学习到的有效特征使用随机傅里叶特征进行核近似,再输入线性单类支持向量机,使提出的模型具有更高的准确率与鲁棒性。
提出的模型在于将深度网络提取丰富特征表示的能力与OCSVM目标函数相结合,获得超平面以将所有正常数据点与原点分开。
本文的其余部分安排如下:第2节回顾了CAE与OCSVM和核近似的背景;第3节详细阐述了本文提出的混合模型;第4节介绍了所用的数据集、实验设置等;第5节对试验结果进行了分析与讨论。最后对本文进行了总结。
1 相关技术
1.1 深度卷积自编码器
自动编码器模型由Rumelhart等人提出[13],AE(auto-encoder)被认为是一种无监督的全连接单层神经网络,可以从未标记的数据集中学习特征表示。AE的核心思想是重建数据的原始模式,从而获得数据的降维表示。
最原始的自编码器网络是一个三层的前馈神经网络结构,由输入层、隐藏层、输出层(重构层)构成,如图1所示。整个自编码器由下面两个操作组成。

图1 自编码器基本结构
一是编码,数据从输入层到隐藏层的过程,其过程如式(1)所示:
h(x)=f(WTx+b)
(1)
其中:f是激活函数,x=(x1,x2,…,xn)∈Rn是输入向量,n表示输入层神经元的个数,h=(h1,h2…,hk)∈Rk是隐藏层的向量,表示输入向量的低维压缩表示,k表示隐藏层神经元的数量。W∈Rn×k是输入层与隐藏层连接的权重矩阵,b∈Rn×1是输入层的偏置向量。
二是解码:数据从隐藏层到输出层的过程,其计算过程如式(2)所示:

(2)

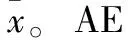
(3)
AE和DAE(deep auto-encoder)的主要局限性在于它们无法捕获图像和视频序列中的二维结构,这样的特性将导致网络参数的冗余,并且去除了可以从图像中提取的局部信息,而这在异常检测场景中特别重要,因为异常位于图像中。为了解决这个问题,Masci等人提出了CAE体系结构[14]。CAE与普通AE类似,卷积自编码器(CAE)将卷积神经网络(CNN,convolutional neural network)中的卷积滤波的优点与自动编码器的无监督预训练结合在一起。但它们之间的区别在于,在CAE中,权重在输入的所有位置之间共享,从而保留了二维空间的局部性,类似CNN[15]。损失函数类似于AE,如式(4)所示。
(4)

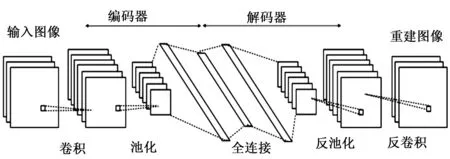
图2 卷积自编码器体系结构
即编码器和解码器分别由全连接改成卷积与反卷积操作,通过外层的池化与反池化将整个网络贯穿起来。CAE的编码过程包括卷积操作与池化操作,卷积操作表示为:
hk=σ(x*Wk+bk)
(5)
其中:hk表示第k个卷积面,σ表示激活函数,Wk和bk分别表示第k个权值和偏置,*表示二维卷积操作。卷积操作完成后进行池化,池化的方法包括最大池化,平均池化与随机池化,本文选择最大池化。CAE的解码过程包括反池化层,反卷积层;反卷积层通过反卷积执行卷积层的逆运算。反卷积层中的学习滤波器用作重构输入形状的基础,并考虑了所需的输出维度,如式(6)所示:
(6)

1.2 单分类支持向量机
Scholkopf等人[16]提出了单分类SVM,把SVM从二分类扩展到了单分类。给定一组训练向量xi∈Rn,i=1,…,N,其中所有的训练向量都属于同一个类。OCSVM构建了一个超平面,该超平面基本上将所有目标类数据点与原点分开,并使该超平面与原点的距离最大化。这主要是通过解决式(7)所示的优化问题来完成的。
s.t.ωTφ(xi)≥ρ-ξii=0,…N,
ξi≥0,i=0,…N
(7)
决策函数表示为:
(8)
如果xi属于目标类,取值为1,否则取值为0。其中,ω是权重系数,φ(·)是特征空间中的映射,K是核矩阵,ai是拉格朗日乘数,N是训练样本总数,v是一个控制训练集中离群点比例的正则参数,ρ是偏差项。决策函数中的ai可以通过公式(9)所示的对偶问题来获得。
(9)
其中:Qij=K(xi,xj)=φ(xi)Tφ(xj)。
从上述描述可以看出,为了寻找最优超平面的问题,即 OCSVM 的决策边界,超参数选择的至关重要[17]。为了解决这个问题,本文使用铰链损失函数来取代(7)式中的ξi。则式(7)转换为一个无约束的优化问题,如下式(10)所示:
(10)
其中:h(xi) 表示卷积自编码器的最后隐含层的输出。
1.3 随机傅里叶特征
为了解决核机器学习的可扩展性问题,核近似算法被广泛应用,由于随机傅里叶核近似方法具有较低的复杂度,且不需要预训练,因此本文主要采用RFF。Bochner定理[11]保证,只要核函数满足平移不变性,连续性和正定性,就存在一个概率分布p(·)的傅里叶变换与k(·) 对应,即:
(11)
其中:p(w) 是w的概率密度函数,对于高斯核函数,通过k(x,y) 的傅里叶逆变换计算p(w),可得w~N(0,2γI),其中I表示单位矩阵。利用标准蒙特卡洛近似积分方法逼近高斯核,D维独立同分布的权重向量(w1,w2,…wD) 可以从分布p(·) 中进行采样,核函数的偏移余弦映射如式(12)所示。
(12)
其中:wi∈Rd服从正态分布N(0,2γI)。应用核近似映射,非线性单分类支持向量机的无约束目标函数变换为:
(13)
2 提出的模型
这部分详细阐述基于CAE与OCSVM的组合模型,即深度卷积自动编码—单分类支持向量机(CAE-OCSVM)模型,用于高维和大数据集的异常检测的任务。该模型由两个主要组件组成,如图3所示。
义乌出口跨境电商企业在高速增长的同时,也面临着诸多不利因素。调查数据显示,10人以下跨境电商企业占66.67%,100人以上企业不到5%,运营时间超过3年企业少于30%,年交易额在人民币1000万元以内企业有70.37%,年销售额到达亿元的企业不足10%。与杭州、上海、深圳等地区的企业相比,义乌中小跨境电商出口企业数量多规模小,经营过程中要承担更高概率和更深程度的风险,因此,如何促进中小企业做大做强成为出口跨境电商的重要研究内容之一。
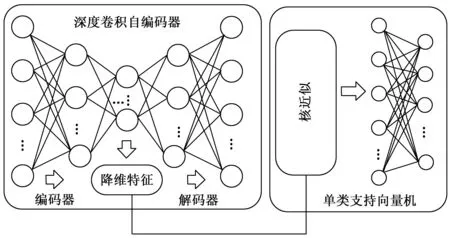
图3 提出的CAE-OCSVM框架模型
深度卷积自编码器主要用于降维,获得输入图像的压缩表示。单分类支持向量机向量机主要用于异常检测,为了使OCSVM也适用大规模高维数据集,本文使用随机傅里叶特征进行核近似。模型中卷积自编码器的瓶颈层的特征经核近似后直接作为线性OCSVM的输入,同时进行训练以优化两个模型的变量参数,这将会使得卷积自编码学习到的特征更有利于OCSVM把正常数据与异常数据区分开来。

(14)
其中:
(15)
式(15)表示卷积自编码器的重构误差,z是如公式(12)所示的随机傅里叶映射,α是平衡卷积自编码器重构损失与OCSVM间隔优化的超参数。从公式(14)的目标函数可以看出,在模型训练过程中,不仅考虑了单分类SVM的损失函数的最小化,而且也考虑了深度卷积神经网络的重构误差的最小化优化,在两者的作用下,将会学习到数据更加本质的特征表示,这将便于提高异常检测的准确性。目标函数使用梯度下降法进行优化,具体如算法如表1所示。

表1 提出的算法流程
3 试验配置
本文的方法以无监督的方式从高维数据中检测异常。在4个公开数据集上进行了试验,并与主流无监督方法进行了比较。4个公开基准数据集分别是MNIST, Fashion MNIST,CIFAR-10,STL-10,详细描述如表2所示。在某些应用中,异常情况具有通用性,例如入侵检测[18],从搜索引擎检索图像[19]等。针对这些应用,从每个数据集中选择一个类别作为普通类别,而将其余类别视为数据集中的异常类别。本文使用AUC(Area Under Curve)作为模型的性能评价指标。

表2 实验数据集
3.1 数据集介绍
MNIST:它包含70 000张黑白手写数字图片,类别从0~9,本文试验中选择某一类别作为异常类,样本是28*28的二维灰白图像。
Fashion MNIST:它是一些流行服饰的数据集,包含10个类别,跟MNIST类似,也是70 000张灰白图像,格式也是28*28的二维灰白图像。
STL-10:它与CIFAR-10类似,也是10个类别,每个类别包含1 300张彩色图像, 800张作为训练集,500张作为测试集,图像的尺寸是96*96*3。
3.2 基准方法
CAE-OCSVM模型与文献[20]的模型单类支持向量机(OCSVM),局部离群因子(LOF,local outlier factor),隔离森林(IF,isolation forest),深度卷积自编码器(DCAE,deep convolutional autoencoder)和深度支持向量数据描述(Deep SVDD,deep support vector data description)、深度嵌入聚类(DEC,deep embedded cluster)以及DAESVM的异常检测方法进行了比较。
3.3 数据预处理与参数设置
3.3.1 预处理
根据式(16),利用max-min归一化将所有输入图像的数值映射到[0,1]范围,进行归一化处理。
(16)
其中:xi为数据的属性值,min为该数据属性的最小值,max为最大值。
3.3.2 模型配置
本文采用的深度卷积自编码器的网络结构如图4所示,这个结构包含3个卷积层,3个反卷积层与1个稠密层,在稠密层上使用L2正则化。在编码器部分的过滤器的尺寸分别为5*5,5*5,3*3,卷积操作的步长为2*2,使用ReLu激活函数。稠密层的神经元数量是10,这样可以得到一个10维的压缩特征。本文采用Adam优化算法来进行神经网络的训练,所有数据集的学习率设置为0.001,每个数据集的最小训练批次与训练次数如表3所示。

图4 深度卷积自编码器结构

表3 训练参数设置
4 结果与讨论
为了评估该方法的总体性能,在4个公开可用的数据集上进行了实验,并与异常检测的5个常用方法的AUC进行了比较。 此外,分析了异常率的影响并将其与其他方法进行了比较。
4.1 4个数据集上的AUC比较
在4个高维数据集上评估了本文提出的模型,这些数据集的描述如表2所示。表4至表7显示了所提模型在MNIST, FASHION MNIST, CIFAR-10和STL-10数据集上的实验结果。每个结果都是运行五次的平均值。从以下表格可以看出,CAE-OCSVM模型优于其他经典异常检测方法,4个数据集的平均AUC为0.930、0.859、0.656、0.672。在表4的MNIST数据集中,尽管当正常类别分别为数字5、6和7时,LOF的AUC略高于所提模型,但所提模型总体上显示出更好的性能。在Fashion MNIST数据集上,从表5中可以看出,当正常类别为Dress与Shirt时,LOF模型的AUC分别为0.883和0.787,要高于本文模型的0.841和0.689,在其余类别以及平均AUC方面,本文模型的性能会更好。CIFAR-10的结果列于表6,当正常类别为Airplane,Cat,Dog和Ship时,CAE-OCSVM表现出良好的性能。 尽管对于其他正常类别,本文模型表现并不特别令人满意,但CAE-OCSVM的总体AUC达到了最佳,平均AUC为0.656。表7显示了数据集维度为27,648的STL-10的结果,当正常类别为Deer,Dog,Truck时,CAE-OCSVM的AUC性能略低于方法IF,特别是在类别Truck中,模型的性能低于IF、DCAE和OCSVM,但整体上可获得最佳性能。 其平均AUC为0.672,大于其它方法的AUC。

表4 模型在MNIST数据集异常率为0.1情况下的平均AUCs

表5 模型在Fashion MNIST数据集异常率0.1情况下的平均AUCs
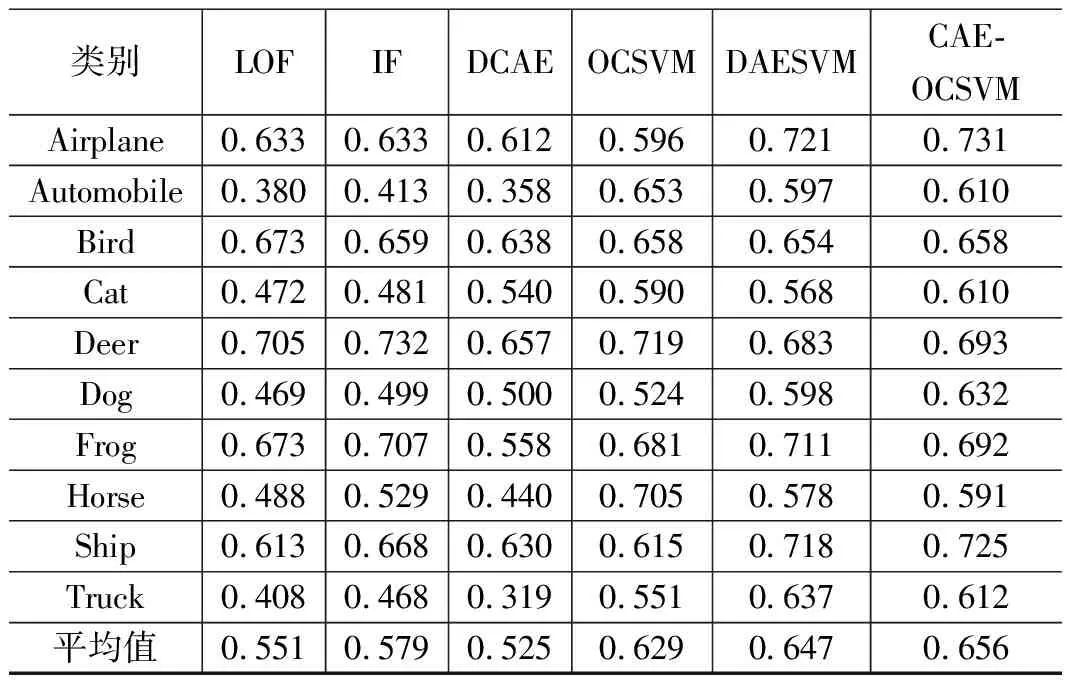
表6 模型在CIFAR-10数据集异常率0.2情况下的平均AUCs

表7 模型在STL-10数据集异常率0.2情况下的平均AUCs
4.2 数据集中异常率的影响
本文为了验证所提出模型的鲁棒性,设置异常率为0.1到0.5,试验结果如图5所示。从图5可以看出,本文模型的AUC值在不同的数据集以及不同的异常率中都是最大的。此外,从图5也可以看出,随着的异常率的变化,本文所提模型的AUC值的波动是最小的,而其他模型的AUC值却随着异常率的增加而下降较大,这充分验证了所提模型具有更强的鲁棒性与泛化能力。从图中结果可以看出,随着异常率的增大,各个模型的AUC性能基本上是呈下降趋势的,这也证明了模型对样本中存在少量异常点的异常检测能力。从图中也反映出了深度学习与OCSVM结合的模型在

图5 4个数据集上不同异常率的性能分析
异常率较小的时候,效果显著,DAESVM与CAE-OCSVM在异常率0.1~0.3之间时,两个模型的性能是最优的,这也体现了这种混合模型适合具有少量异常样本数据集的异常检测。
4.3 模型复杂度分析
根据提出的模型可知,模型主要包含深度卷积自编码器和单类支持向量机,模型的时间复杂度主要是两者时间复杂度之和,由文献[21]可知,卷积自编码器的时间复杂度为:
其中:K为卷积自编码器的卷积层数,M2为特征图面积,S2为卷积核面积,k表示第k个卷积层,Ck为第k个卷积层的卷积核个数。
而提出的模型的优势在于卷积自编码器器输出后进行核近似,然后通过线性支持向量机进行异常检测,故重点分析一下核近似支持向量机的时间复杂度的提升。假定训练集样本数为n,d为深度卷积自编码器的输出维度,也就是样本降维后的维度,D为随机傅里叶特征的空间维度,由文献[22]可知,使用SMO算法训练高斯核SVM的时间复杂度为O(n2),而求解线性支持向量机的时间复杂度为O(nD),随机傅里叶特征映射的时间复杂度为O(nDd);在单类支持向量机的参数设置中,本文使用k折交叉验证来决定高斯核的参数γ和正则化参数ν,令α,β分别表示搜索网格的长度,则高斯核SVM的时间复杂度为t0=O(kαβn2)线性SVM的时间复杂度为t1=O(kαβnD),随机特征映射的时间复杂度为变为t2=O(αnDd),那么从核近似到训练线性支持向量机的总的时间为随机特征映射的过程所花费的时间与训练单类支持向量机的时间之和,即TOCSVM~t1+t2,故所提模型的时间复杂度为T=TCAE+TOCSVM。
由分析可知,高斯核OCSVM的时间复杂度与样本数量的平方成正比,而核近似之后,经线性OCSVM训练的时间复杂度与样本的数量成线性关系,远远小于核支持向量机的训练时间。这充分证明了所提模型的高效性。
5 结束语
本文提出了一个新的图像异常检测模型,模型联合深度卷积自编码器与单分类支持向量机,深度卷积自编码器负责图像降维以及特征表示学习,单分类支持向量机负责异常检测。同时使用随机傅里叶特征对单分类支持向量机的核函数进行核近似,把3种技术联合起来,构建了一个新的模型目标函数,目标函数能够学习到数据集的本质特征,实现了一个端到端的训练模型。模型在4个图像数据集上进行了实验验证,并且与不同的异常检测模型进行了性能对比,从实验结果来看,提出的模型在整体性能方面优于其它异常检测模型。模型还在不同的异常率的情况下进行了实验,结果证实,提出的模型具有更好的鲁棒性与泛化能力。下一步将重点在多核近似方面进行进一步的研究,来进一步提高模型的泛化能力,同时将在更多的数据集上进行实验验证。
