改进孪生网络的脑电信号处理方法

杨怀花，叶庆卫，罗慧艳，陆志华

(宁波大学 信息科学与工程学院,浙江 宁波 315211)

0 引言

脑机接口(BCI,brain computer interface)是一种不依赖大脑外周神经与肌肉组成的正常输出通路，通过对大脑活动产生的信号进行分析，提取其中包含的动作意图，控制外部设备的新型人机交互方式[1]。脑机接口技术的研究对临床康复[2]、信息交流[3]以及休闲娱乐等领域的发展均具有较高的价值。目前，脑机接口方向的研究众多，运动想象脑电信号(MI-EEG，motor imagery electroenceph- alogram)作为自发性脑电一直以来受到研究学者的广泛关注。MI-EEG信号是一种时变性很强的非平稳信号，因此如何有效的对其进行特征提取和分类成为了目前研究的重点。

当前脑电信号特征提取的研究主要分为4个方面：时域、频域、时频域以及空间域等，常见的分析方法主要包括小波变换[4](WT,wavelet transform)、希尔伯特黄变换[5](HHT,hilbert-huang transform)、公共空间模式[6-8](CSP,common spatial pattern)、独立分量分析[9](ICA,independent component analysis)等，常用的分类方法主要包括线性判别分析[10](LDA,linear discriminant analysis)、支持向量机[11](SVM,support vector machines)、贝叶斯线性回归[12]、卷积神经网络[13](CNN,convolutional neural networks)等。由于深度学习的快速发展，神经网络成为了脑电信号识别分类的重要方法。

目前针对运动想象脑机接口系统中分类准确率低等问题，研究者们提出了很多改进方法。文献[14]提出了一种基于滑动窗口信息极大化原则(Infomax，information maximization)算法的动态独立分量分析方法。文献[15]提出了一种优化多球面支持向量数据(SVDD,support vector data description)的模糊聚类方法，并通过多个运动想象数据集的实验，完成了对运动想象脑电信号数据的较好的表达。文献[16]提出一种新的基于沃尔什哈达玛变换的特征提取方法，将提取的特征通过人工神经网络进行分类，得到较为准确的结果。文献[17]提出将从脑电信号中提取的时间、频率和位置信息，组合成2D信息输入到卷积神经网络(CNN，convolutional neural network)和堆栈自编码器(SAE，stacked auto encoder)结合的深度网络，得到较高的分类准确率。

基于以上的研究内容，本文提出一种3个权重共享子网络构成的改进孪生网络，将经小波变换结合经验模态分解预处理后的信号输入此网络，实现对脑电信号的特征提取和分类。通过对两个数据集的仿真，相比现有算法均取得更好的分类准确率，表明此方法能更好的应用到MI-EEG信号的分类识别，并具有一定普遍性。

1 算法原理

1.1 孪生网络改进原理

经典孪生神经网络由两个子网络构成，这两个子网络之间结构相同，并且共享权重和偏置等参数。若样本(x1，x2)和标签y输入孪生神经网络，其中输入样本类别相同标签y为1，相反标签为0，通过权重共享的子网络提取样本的低维特征，计算特征的距离度量样本相似度。代价函数为对比损失函数公式如下：

L(w,(y,x1,x2))=

(1)

其中:DW为输入样本经过孪生神经网络提取的低维特征之间的欧式距离，公式为DW(x1,x2)=‖f(x1)-f(x2)‖,f(x1)、f(x2)分别表示样本x1、x2经过神经网络映射出的低维特征，y为样本标签，max表示最大值，m为设定的阈值。

本文提出一种3个权重共享的子网络孪生系统如图1所示，其主要包括两部分：特征提取和相似度计算。在特征提取部分，本文选取5层的全连接神经网络。表1是网络结构的详细说明。为了防止过拟合现象，每层全连接层后使用dropout函数。对于大部分数据来说，ReLu 激活函数具有更好的拟合能力。因此隐藏层选取非线性的Relu作为激活函数，输出层则使用sigmoid 激活函数，使得结果介于0到1。

表1 网络结构

图1 改进孪生网络框架

当输入脑电信号样本组合x1、x2、x3时，通过3个共享权值的子网络提取低维特征，计算样本特征之间的平均距离来表示样本之间的差异，最后利用这个距离进行相似度判断。本文提出一种新的距离函数，如公式2所示：

DW(x1，x2，x3)=

(2)

其中:x1和x2、x3为输入的样本序列，f(x1)、f(x2)和f(x3)为经过神经网络提取的低维特征，DW(x1，x2，x3)为特征之间的平均距离，采用公式(1)作为损失函数进行训练。此距离函数消除了样本因随机选取产生的偶然性误差，使分类系统更加稳定，一定程度的提高了分类的准确度。

1.2 学习样本集采样算法

设预处理后的训练集为Xtrain、Ytrain，其中Xtrain为预处理后的小波分量训练集信号，Ytrain为训练集样本标签。

(3)

3)令i=1,…,n，因此可以得到包含n个样本组的学习样本集。

1.3 测试集样本采集

设预处理后的测试集为Xtest、Ytest，其中:Xtest为预处理后的小波分量测试信号集，Ytest为测试集样本标签。

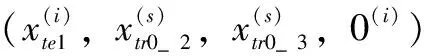
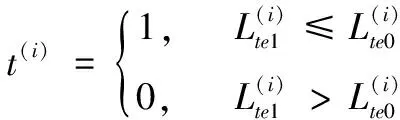
(4)

4)令i=1,…,l，其中l为预测样本长度。即依次对测试集Xtest中所有样本进行上述操作，可得到Xtest的预测标签。

1.4 信号预处理过程

脑电信号是一种非线性、非平稳的信号，小波变换是在一种时频域分析方法，更好的分析和处理了非平稳信号，早在1996年就被应用于运动想象脑电信号的去噪处理。对信号x(t)进行分解，其离散小波函数表示为：

(5)

其中:ψj,k(t)为基本小波。

由于脑电信号的电压普遍在μV量级，这一特点导致EEG信号极易受到眼动、肌电、高频噪声等干扰。因眼动干扰处于低频段并与脑电信号重叠，使得其去除较为复杂，而肌电和高频噪声则处于高频段。若将噪声相关的频段直接去除，则会导致一部分重要信息丢失，因此本文选取小波分量的最低频段和最高频段进行经验模态分解(EMD,empirical mode decomposition)，通过自相关函数将EEG信号与噪声信号尽可能进行分离。

EMD分解是一种非线性滤波器，将信号分解为若干个IMF，其中IMF需要满足以下两个条件：

1)整个数据中，极值点和过零点数目相等或最多相差为1。

2)在任意一点，由局部极大值定义的包络和由局部极小值定义的包络的均值等于0。

自相关函数选取的是脑电自身信号与时延后的信号之间的相似度，其表达式为：

(6)

其中:x(t)为原始运动想象脑电信号，Δτ为延时长度，Cov表示协方差，var则为方差。干扰噪声一般表现为低频、高幅度，因此对于含噪声成分较高的IMF分量，自相关函数较高。而脑电信号具有随机性较强、时变复杂等特点，因此其值较低。通过设定自相关阈值，筛选出脑电信号相关的IMFs分量进行重构，得到“纯净”的小波系数。

1.5 总体算法流程

算法流程如图2所示，主要步骤为：

图2 算法流程

1)将脑电信号进行预处理，然后经过5折交叉验证法将信号集分成训练数据和测试数据。

2)根据1.2节学习样本集采样算法构建三样本组合学习样本集，将其作为三权值共享的孪生神经网络的输入，根据对比损失函数，利用全连接神经网络更新权值和偏置等参数。当模型收敛或者到达设定次数时，模型训练结束，保存模型。

3)在测试过程中，根据1.3节依次对所有测试样本构造正负测试样本集，对比正负测试样本集平均距离，选择最小平均距离(即相似度最高)所对应的类别作为该待测样本的类别号。

2 实验仿真与分析

2.1 实验数据

本文提出的方法得到来自The largest SCP data of Motor-Imagery和BCI Competition II Data set III两个数据集的验证，接下来对其进行介绍。

数据集1来自公开标准数据集BCI Competition II Data set III，该组数据是通过年龄为25岁的健康女性进行想象左右手实验获得的。本实验共进行了7组,每组40次,共进行了280次试验。每一次试验持续时间为9秒, 在0～2秒时为休息时间；在第2秒时进行语音提示；第3秒开始屏幕上出现一个箭头，同时要求受试者进行相应的运动想象。数据的采集电极放置在国际标准的10～20导联系统c3、cz、c4位置，其中采样频率为128 Hz。实施示意图如图3所示。

图3 实施示意图

数据集2来自2018年提出的国际标准脑电信号数据库The largest SCP data of Motor-Imagery中的CLA左右手运动想象数据集，此数据集是由7名健康受试者(S1～S7)面对图形用户界面(eGUI)的相应提示执行左手、右手运动想象。数据的采集电极放置符合10～20导联标准，每组数据包含21个通道的EEG信号，采样频率为200 Hz。实验过程中，图形用户界面上显示一个左右手两类刺激信号，动作信号在屏幕上保持1秒，同时受试者执行了一次相应的心理意象，随后暂停1.5～2.5 s后结束单次试验，每段记录持续50～55分钟。对于7名实验对象采集的数据信息如表2所示。

表2 数据集信息

2.2 预处理过程

图4分别为数据集1左右手运动想象时通道c3、cz、c4的平均能量。由图(a)可知，cz通道的左右手想象运动能量几乎没有区别，由图(b)和图(c)可知c3、c4通道3.5～9时间段的平均能量差别较大，因此本文选取3.5～9时间段的c3、c4通道脑电信号进行小波变换。

图 4 各通道的信号平均能量图

在进行小波变换时，小波基[18-19]和自相关系数阈值的选取对脑电信号的处理影响较大。本文通过选取部分小波基用于离散小波变换，分别为dmey、db2、sym3、haar，经过多次实验对比，发现选取demy小波基分类准确率更高，稳定性更强。相关系数阈值是一个重要的参数，其值直接影响了伪迹与脑电信号的分离，在保持其他条件不变的情况下，采用不同阈值得到分类准确率。经过多次试验当阈值等于0.9时，正确率高达90%以上，因此本文选取0.9为相关函数阈值。

数据集1选取脑电信号样本3.5～9时间段的C3、C4通道脑电信号分别进行4层小波变换，其中选用demy为小波基，然后对小波分量的低频部分A4和高频段D1进行经验模态分解，将IMFs分量的自相关函数值小于0.9的进行重构，得到“干净”的小波分量，然后将各个通道的小波分量进行串接。

数据集2对21通道脑电信号进行5层小波变换，其中选用demy为小波基，然后对小波分量的低频部分A4和高频段D1进行经验模态分解，将IMFs分量的自相关函数值小于0.9的进行重构，得到“干净”的小波分量，然后将各个通道的小波分量进行串接。

2.3 评价指标

分类精准度被用来直接衡量信号分类的准确率，其公式为：

(7)

其中:TP和TN为左右手想象信号正确识别样本数量，FP和FN为左右手想象信号错误识别样本数量。

Kappa值是一个信号分类一致性的评价指标，其公式为：

(8)

其中:p0是总的分类正确率。对于二分类而言，每一类实际样本数为r1、r2，则每一个类别中预测样本个数p1、p2，pe则为：

(9)

2.4 实验结果

下面运用数据集1，对脑电信号进行预处理后，分别通过经典孪生神经系统和改进后的孪生神经网络进行脑电信号特征提取和分类，同时得到两种方法在测试集上的分类混淆矩阵如图5所示。由图5可知，改进孪生网络在左右手想象信号相比经典孪生网络均具有更好的可分性，测试集上的识别精度更高。

图5 经典和改进后孪生网络混淆矩阵

将本文的算法与目前性能较高的现有算法进行对比，其中用到对比算法主要有文献[14]中基于滑动窗口Infomax算法的动态独立分量分析方法，记为 ICA，文献 [15]使用AR算法和优化多球面支持向量数据的模糊聚类方法相结合的方法，记为AR-SVDD。文献[16] 中基于快速沃尔什哈达玛变换的特征提取方法，并结合ANN分类器进行分类，记为FWHT-ANN。文献[17]中CNN结合SAE提出的一个新的深度网络，记为CNN-SAE算法。文献[20] 提出的Renyi熵特征提取方法，结合BLDS分类器对信号进行处理，记为Renyi-BLDA。将经过小波变换结合经验模态分解预处理后的信号，输入经典孪生神经网络进行特征提取和分类的方法，记为WT_emd_siamese。分类结果如表3所示。

表3 不同特征提取算法的分类正确率

从表3可知，本文算法分类准确率均高于其他算法，其准确率提高了4.29～13.06%，表明所提算法能更好地实现脑电信号处理。WT_emd_siamese算法分类正确率到达87.50%，进一步证明了小波变换、经验模态分解结合孪生网络方法的可行性，这为运动想象脑电信号处理提供了一种新思路。

2.5 算法在不同数据集的进一步验证

为了进一步验证算法的有效性，对数据集2进行测试，并采用目前较为常用并取得较好结果的csp算法结合svm分类器办法进行基准验证，结果如表4所示。由结果可知，此方法平均分类正确率高达到90.36%，相对csp_svm分类性能提升了12.5%，且最高达到97.43%，去除数据集S2和S6实验对象，平均分类准确率高达94.30%，进一步证明了此算法在脑电信号识别方面具有较好性能。此外，本文提出算法kappa值高达0.907，其具有较好的一致性，分类结果可靠。

表4 数据集2所有受试者分类正确率

图6显示了在数据集2上两种算法测量的总分类混淆矩阵，如图6中数据显示，本文所提出的算法，相比csp_svm脑电信号处理办法，无论在左手还是右手识别中精确度都得到极大地提升，其中左手识别精度到达96.7%，这也证明了本文算法在运动想象任务中发挥着积极地作用。

图6 混淆矩阵

3 结束语

本文提出一种3个权重系数共享子网络构成的改进孪生网络脑电信号的分类方法。通过小波变换结合经验模态分解，对信号进行预处理，然后将预处理的小波分量通过改进的孪生神经网络系统进行特征提取和分类。将改进后的孪生网络与经典孪生网络相比，利用新的距离函数消除了偶然误差性，提高了分类正确率，使分类系统更加稳定，同时在特征提取部分选择简单的全连接神经网络，在保证了分类性能的同时，极大地降低了系统的复杂性。通过对BCI Competition II Data set III数据集进行仿真，本文提出的算法取得了94.29%的分类准确率，与现有的研究结果进行对比，可以更有效地进行运动想象脑电信号的分类。利用The largest SCP data of Motor-Imagery数据集进一步验证，结果表明本文提出的方法在相同的数据类型下依旧保持优异的性能。因此在接下来的研究过程中，可将此方法应用到其他类型的脑电信号分析，这为脑电信号处理提供了一种新思路。