分布式系统TTCAN调度优化算法研究
2022-03-30叶彦斐刘之境赵金玉
叶彦斐,刘之境,刘 帅,赵金玉
(河海大学 能源与电气学院, 南京 211100)
0 引言
CAN(controller area network)总线作为应用最广泛的现场总线之一,为分布式控制系统实现各节点之间实时、可靠的数据通讯提供了强有力的支持[1]。随着总线技术的发展,线缆测试仪也逐渐产生了分布式、信息化及网络化发展的新需求。在分布式线缆测试仪实际工作中,数千条测试线路数据需要同时传输、通信,其中不仅包括诸如通断检测状态、绝缘检测状态等需要优先处理的消息,也包括主机设置、信息查询、节点自检等等非周期性消息,从而对总线的稳定性及通讯效率提出了更高的要求。因此,需要设计或改进优化一种更高效、更可靠的基于CAN总线的应用层通讯协议,来更好地满足分布式线缆测试仪的需求。
TTCAN(Time-Triggered CAN)是一种以系统矩阵为核心,基于时间触发的总线协议。论文采用TTCAN作为分布式线缆测试仪中数据传输的应用层协议,针对TTCAN的系统矩阵进行优化设计,采用遗传算法、差分进化算法和动态优先级算法分别为线缆测试仪的周期性和非周期性消息调度策略进行设计及优化,以实现提高系统稳定性及总线传输效率的目标。
1 TTCAN的系统分析
TTCAN协议的核心是其独有的系统矩阵,其完整的传输周期被称为系统矩阵周期MP(Matrix Period)[2],一个MP具有多个基本周期BP(Basic Period)。单个基本周期BP由一个参考消息开始,对应系统矩阵中的一行。分布式线缆测试仪的系统矩阵中会存在若干周期性或非周期性消息,如图1所示。

图1 TTCAN的系统矩阵周期

2 TTCAN调度计划分析
2.1 TTCAN消息分析
一般来说,通讯系统中的消息被分为两种:时间触发消息和事件触发消息,这种分类隐藏了一个很重要的特征:消息的真实时间需求。
在通信系统中,按照任务的时延需求可以将消息分为3个种类[3]:硬实时消息、普通实时消息以及软实时消息,而在分布式线缆测试仪中,不同的消息种类对于时间延迟的要求也不同,诸如线缆通断、绝缘以及振动测试结果,必须及时从从站传输到主站,属于优先级最高的硬实时消息,必须安排在独占窗口中进行即时通讯。而诸如线缆测试启动、测试结束等按键指令,为了保证操作的流畅度,也应有较高的优先级。诸如各种设置、查询类消息属于普通实时消息,虽然也需要及时处理,但在测试过程中并不是特别重要,所以可以安排至仲裁窗口或自由窗口中。主机自检、LED自检等功能则划归为软实时消息,仅需在机器空闲时进行即可,不需要严格的响应时间要求。
对线缆测试仪的消息分析表明,一些比较重要的消息也可能被分配到仲裁窗口中,那么这类消息的通讯效率就会受到仲裁机制的影响,仲裁窗口中的其它普通消息也需要减少传输延迟。综上,扩大仲裁窗口的传输时间有利于整个系统性能的提高。论文的主要工作是保证硬实时消息及时传输的同时,最大限度地提高仲裁窗口传输时间。
2.2 构建初始矩阵
PSA(标致雪铁龙集团)消息集常用于基于现场总线的分布式系统的基准测试[4],论文选择PSA消息集模拟线缆测试中可能出现的消息通信情况,以验证通信优化方法的可行性,并增加了一些延时约束使其更符合实际情况。
如表1中所示的修改的PSA消息集可以模拟线缆测试过程中可能出现的周期性消息通讯情况,共有12个硬实时消息需要进行处理,每个消息所需要的传输时间各不相同,并且由于同一条线缆的多项测试结果应在较短时间内完成传输,所以一些消息之间会构成控制环路。为了保证线缆测试系统的时效性,需要使所有消息的传输时间以及消息间形成的控制环路都得到满足。
根据表1中的消息集,可以得到矩阵的系统周期TMP为80 000 μs,基本周期TBP为10 000 μs,共存在8个基本周期[5],那么初始矩阵为8行;按各消息周期时间计算得到在一个系统周期内总共需传输的消息数为52,至少需要7列进行消息集传递,加上每行第一列参考消息和最后一列仲裁窗口,初始矩阵选9列。用相对简单的装箱算法可以得到初始矩阵,如图2所示。
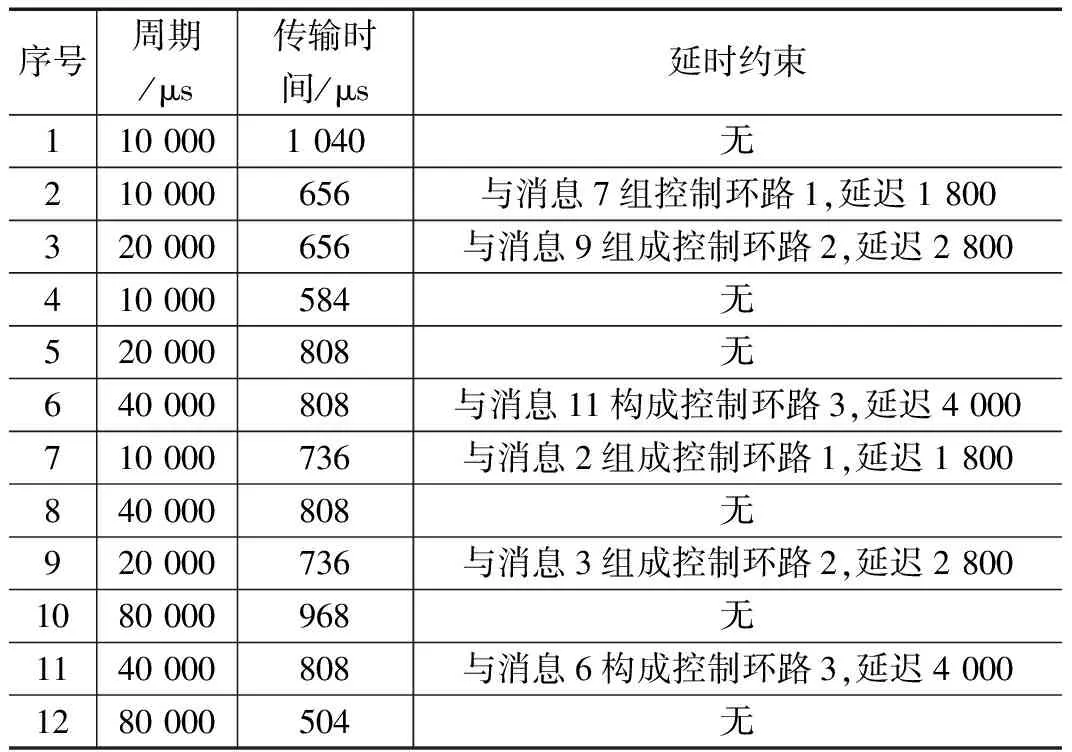
表1 PSA消息集
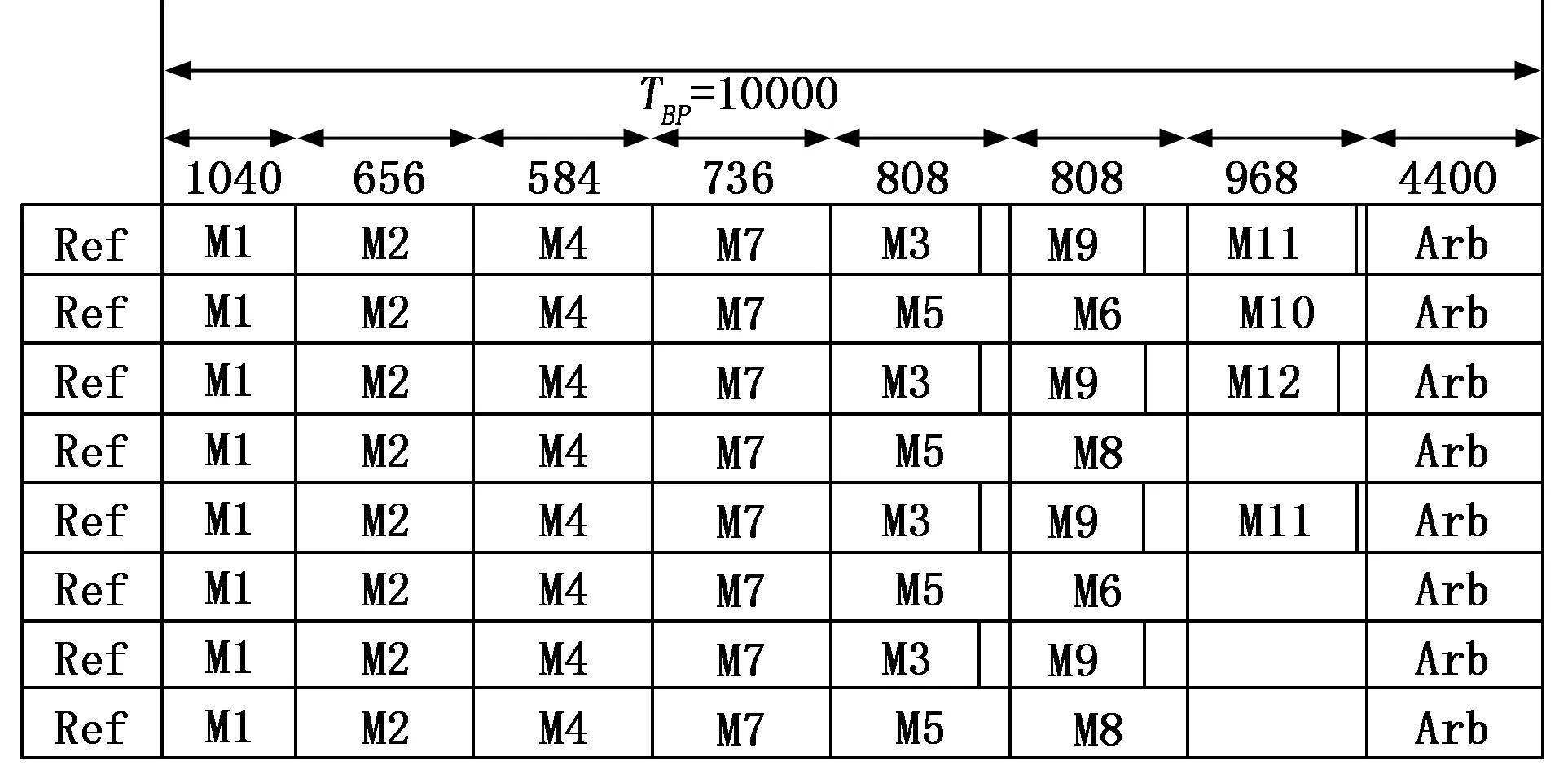
图2 初始系统矩阵
矩阵单列须满足该列中所有消息的传输时间需求,则单列列宽须大于或等于该列所有消息传输时间的最大值,这导致矩阵的独占窗口中存在很多空白区域,这些空白显然会造成总线传输效率的下降[6]。论文通过设计、优化消息调度策略,对系统矩阵中各个消息的合理安排,尽量缩短整个独占窗口的通讯时间,以扩大仲裁窗口、提高总线通讯效率。
3 消息调度优化算法
3.1 周期性消息优化
3.1.1 编码
首先对矩阵进行编码:
如图3(a)所示,将M1至M7所处的列数作为消息编码,如M1处在矩阵第1列,那么M1的编码就是1,可得到图3(b)中M1至M7在矩阵中的编码为[1,1,2,3,2,3,3]。

图3 矩阵编码
同理可得到图2初始系统矩阵中M1至M12编码为:[1,2,5,3,5,6,4,6,6,7,7,7]。
3.1.2 优化目标
设j表示表1中各消息的序号,i表示图2初始系统矩阵的列数。xij根据对应序号为j的消息在某列是否存在取值1或0,若第k列存在,则xkj的值取1,否则取0。
例如,j=3时,消息3存在于第5列,则x53为1,x13、x23…为0。
由于同一个消息只会在矩阵的同一列出现,且每行最多出现一次,可得:
(1)
优化目标可分为两部分,一部分表示独占窗口所占用时间的最小化,另一部分表示总线的利用率。Cj表示消息j所需的传输时间,通过Cjxij表示消息j在某一列中所占用的传输时间因为必须保证任意一列的所有消息都可以正常传输,所以矩阵列宽取该列所有消息的最大值。则最小化独占窗口时间可表示为:
(2)
同时将总线的利用率表示为:
(3)
Tj为消息j的传输周期,将式(2)和式(3)叠加可得到目标函数,以达到减小独占窗口传输时间的同时总线利用率最大化的效果。
3.1.3 条件约束
初始矩阵生成后,矩阵的总行数是固定的,必须对矩阵进行适当的约束,确保整个矩阵每一列消息的数量不能超过该列的初始行数,即单个消息j在矩阵中出现的次数必须小于等于矩阵的行数[7],可得如下的表达式:
(4)
设:
(5)
同时总线须满足延时约束,需要保证控制环路的延时在设定的范围内,根据实际线缆测试情况,若控制环路对应的两个消息的序号分别为j1、j2,其周期都为BCT,对应的列为i1、i2,最大网络延迟可表示为:
(6)
Cmin和Cmax指的是表1消息集中最小和最大传输时间,Cj2为消息j2的传输时间,Td为两消息之间的最大网络延迟,设:
(7)
3.1.4 目标函数
经过总线通讯调度优化,将独占窗口占用时间最小化,总线利用率最大化,同时还需要满足矩阵行数约束和控制环路延迟约束。引入罚函数法对约束条件进行处理,将不等式以罚函数的形式融入目标函数,可以降低优化难度,提高优化效率[8]。将总线利用率取倒数并调整数量级以匹配独占窗口占用时间的数量级,可得到目标函数表达式:
(8)
其中:
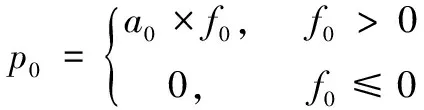
(9)
p1在i2>i1时为:
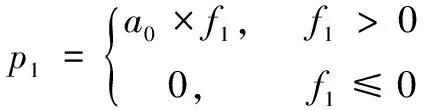
(10)
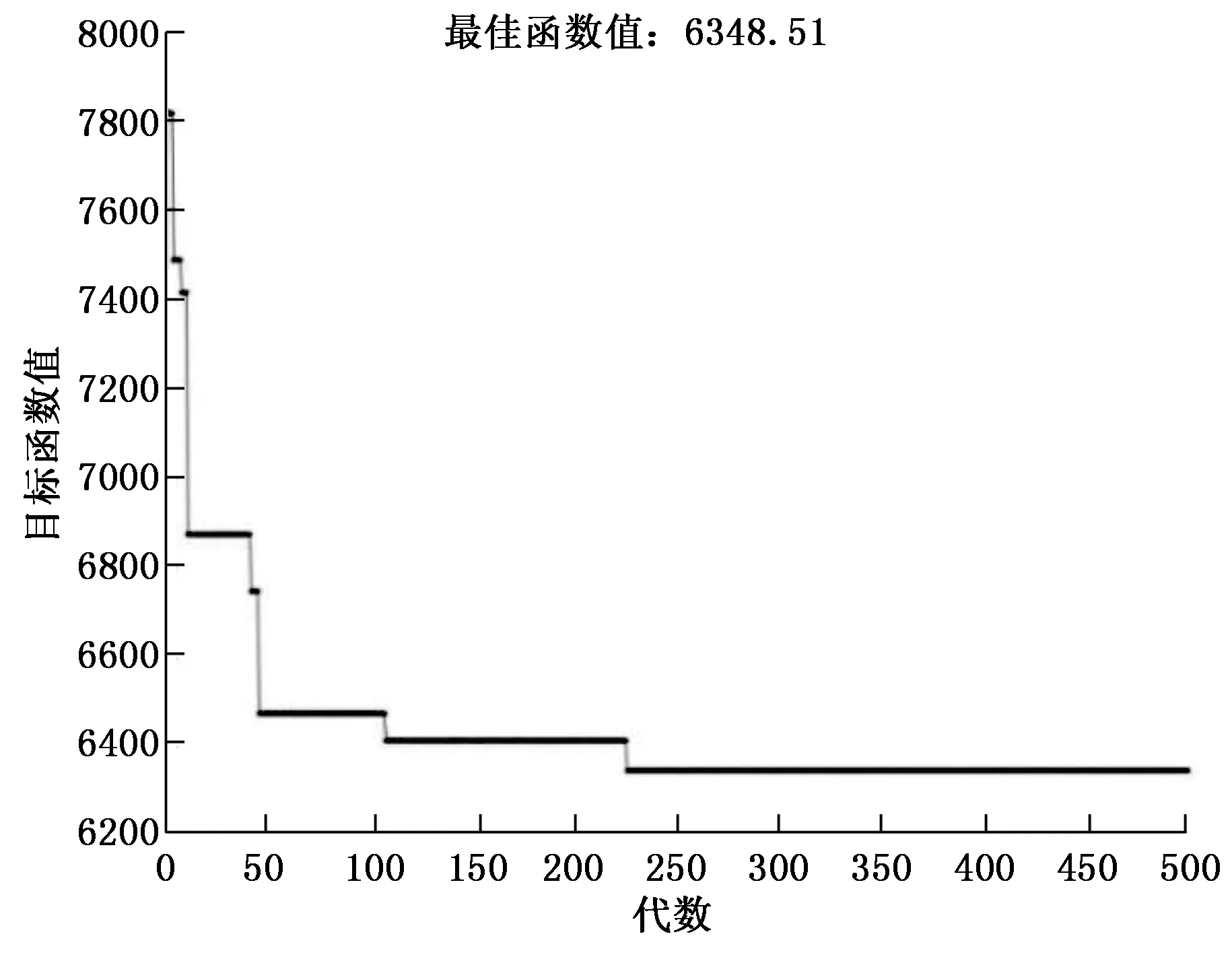
在i2 (11) a0和a1为惩罚因子,一般取较大的常数值。论文中a0取值400,a1取值5 000,不符合约束条件的F值会因此数值过大而被算法淘汰。 差分进化算法可以有效规避算法陷入局部循环的问题,其主要用于求解连续域上的优化问题,论文主要是整数优化,属于离散优化,所以可以借鉴0~1规划中对于差分进化算法的改进[9]。 佳点集法是一种用更少的试验次数产生更加均匀的点序列、更逼近被积函数曲线[10]的初始种群生成方法。该方法有效避免了随机生成初始种群的弊端,且通过佳点集生成的种群精度与维数无关,有效提高了函数的运算效率。因此论文采用佳点集法生成初始种群,其定义为:设Gs为S维欧氏空间中的单位立方体[11],如果r∈Gs,形为: 1≤k≤θ (12) 若偏差φ(θ)满足: φ(θ)=C(r,ε)θ-1+ε (13) 其中:C(r,ε)是只与r,ε(ε>0)有关的常数,则称pθ(k)为佳点集[12],r称为佳点。取: r={2cos(2πk/p)},1≤k≤s (14) p为满足(p-s)/2≥s的最小素数,或: rk={exp(k)},1≤k≤s (15) {a}表示a的小数部分。用任意给定的θ个点的函数值构成的任何加权和来近似计算函数在S维欧氏空间单位立方体Gs上的积分时,取θ个佳点所得的误差是最小的[13],此时最小误差为: (16) 其中:pθ(k)是一个包含有θ个点的佳点集。 其次,为提高算法的局部搜索能力和全局搜索能力,加快收敛速度,采用自适应的变异因子及交叉因子。 变异是差分进化算法的重要步骤,常用变异操作有随机变异法和最优变异法。 随机变异法如式(17)所示选取随机个体变异: υα,β(t+1)=xα,β(t)+F(xp1,β(t)-xp2,β(t)) (17) xα,β表示第α个个体的第β个分量,α=1,2,…,M,β=1,2,…,n。其中p1,p2为[1,M]中任意选取的互相不等的随机整数,M为父代个体总数,F为变异因子,t为当前进化代数,υα,β(t+1)为暂量,参与差分进化算法接下来的交叉、选择操作。 最优变异法如式(18)所示选取最优个体变异: υαβ(t+1)=xbest,β(t)+F(xp1,β(t)-xp2,β(t)) (18) 随机变异法全局搜索能力较强,但收敛速度较慢;最优变异法一定程度上提高了局部搜索能力,但会使算法更容易陷入局部循环。 根据这两种变异的特点,论文提出了渐进的变异策略,如式(19): υαβ(t+1)=λxαβ(t)+(1-λ)xbest,β(t)+ F(xp1,β(t)-xp2,β(t)) (19) 最后针对整数优化,对变异和交叉后的个体取整并求绝对值,以保证算法的解为整数。 3.3.1 松弛度 LLF(Least Laxity First)算法根据消息的松弛度(紧急程度)评估优先级,松弛度越低的消息优先级越高。设Δtp为有效生存期,即消息从生成到截止的时间,设消息从抢占总线到发送成功所需的时间为ti,则消息的松弛度ΔtL=Δtp-ti。总线内的各通讯消息因松弛度不同,优先级会被动态调整。 3.3.2 动态标识符 总线通过对标识符进行仲裁实现消息调度功能,动态调度非周期性消息需要动态调整其标识符。对消息标识符ID的更改会影响其标记消息种类和功能以及作为各节点消息滤波凭据的作用。STM32芯片内部自带bxCAN收发控制器。bxCAN内置的消息过滤器组可屏蔽、位宽可变,可以实现总线消息传输的硬件过滤功能,节约了CPU开销的同时,过滤器组可以选择性过滤标识符ID的部分位[16]。LLF算法对总线非周期性消息的调度通过该功能实现。 3.3.3 实际应用 由于独占窗口中存在一些空闲时间,可将部分非周期性消息通过该窗口进行通讯。将周期性消息标识符最高位设置为1,非周期性消息最高位标识符设置为0,使其优先级低于周期性消息,避免出现堵塞现象。将剩余标识符位中后Y位设定为固定部分用于消息过滤及功能识别,其余位中可变部分设为动态部分,可得系统中可调度的消息数量为2Y。 设总线所有消息的最大有效生存期为Δtpmax,动态部分数值大小为IDdynamic,则由总线各节点完成计算: (20) 为确保有效生存期最小的消息也能够实时发送,应保持调整周期应小于所有消息传输时间的最小值对动态ID进行调节。该功能通过STM32芯片的定时器实现。 针对周期性消息,在MATLAB中先使用遗传算法进行程序设计,以便与改进型差分进化算法进行对比。 首先随机生成初始种群,种群大小选择2 000并用式(8)所示目标函数计算个体适应度。接着采用轮盘赌选择法进行个体选择并进行交叉步骤,交叉后代比例选择0.8[17]。然后进行复制、变异,选择精英数目为50,并将适应度函数值偏差设为e-100[18],迭代结果如图4所示。 图4 遗传算法优化结果图 得到的结果通过矩阵排列如图5所示。 图5 优化的系统矩阵 可以看到独占窗口的通讯时间由图2中的初始化矩阵中所示的5 600 ms降低到了5 448 ms,传输同样的消息量所需时间缩短了2.7%,起到了良好的优化效果。 接着使用上文所述的改进型差分算法对矩阵进行优化,首先通过佳点集法生成初始种群,接着采用式(19)所示渐进变异法对初始种群进行变异,然后引入自适应的交叉指数pc=et-T/T进行交叉操作,最后通过式(9)计算适应度后进行选择操作,通过迭代可以得到结果如图6所示。 图6 差分进化算法优化结果图 可以看到函数在迭代至68代时就已经收敛到了遗传算法计算出的最优值,得到了相同的优化效果。通过比较遗传算法和差分进化算法的进化曲线,发现改进型差分算法收敛速度较快。且在实际的多次实验中发现差分进化算法收敛稳定性高,不容易陷入局部循环。遗传算法已经可以达到对周期消息矩阵进行优化的效果,但是优化速度仍然不够理想,且经常会出现陷入局部循环的现象,而差分进化算法可以有效地规避这样的问题。 非周期消息通讯采用了抢占多任务的结构,在满足任务实时调度的同时,抢占多任务会带来CPU资源的浪费和内存总开销的增加[19]。因此在保证调度质量的前提下,任务切换的频繁程度可以用来评估系统的通信效率,切换越频繁,通信效率越低[20]。通过MATLAB程序仿真比较相同时间内应用算法前后整个总线系统切换次数如图7所示。 图7 系统切换次数仿真图 图7显示,在使用优化算法后系统的切换次数较使用优化算法前有明显降低,证明了优化算法可以有效地减少系统抢占现象,可以显著提高总线传输效率。 论文针对分布式线缆测试仪这一分布式系统的实际应用中可能出现的时滞问题,分别对周期性消息和非周期性消息提出了不同的优化方案,将周期性消息的调度问题转化为整数优化问题,并通过改进型的差分进化算法进行了有效的优化,得到了优化的系统矩阵,提高了总线利用率;对于非周期性偶发消息,通过基于松弛度的动态优先级调度方案,保证了偶发性消息的可靠传输。
3.2 差分进化优化算法改进


3.3 非周期性消息优化
4 仿真结果分析



5 结束语
