基于深度卷积神经网络的点云三维目标识别方法研究
2022-03-30李豪杰杨海清
李豪杰,杨海清
(浙江工业大学 信息工程学院,杭州 310012)
0 引言
三维激光扫描技术被广泛应用于自动驾驶[1]、建筑施工[2]以及遥感测绘等领域[3],其通过三维激光扫描仪或者三维激光雷达等扫描设备来获取被测物体空间和表面纹理等信息,具有分辨率高,采集速度快以及非接触式等优点。三维扫描设备得到的是被测物体的三维点云信息,其抗干扰能力强,不受外界因素影响,从而更有利于目标识别与姿态估计[4]。然而,传统基于三维点云数据的目标识别方法有着计算数据量大以及速度慢等问题[5],因此,对基于激光点云数据的三维目标识别方法进行研究具有十分重要的现实意义。
近年来,学术界对基于点云数据的三维目标识别方法进行了很多相关研究。在以深度神经网络为代表的深度学习还没有兴起之前,计算机视觉领域主要采用传统的机器学习方法对点云目标进行分类和检测,如支持向量机(SVM,support vector machine)[6]和决策树(Decision Tree)[7]等。文献[8]采用基于点云梯度的局部最优分割方法对激光雷达扫描的点云目标进行梯度分割以提取出障碍物轮廓,并根据障碍物三维点云数据特征,利用基于核的支持向量机有效完成了障碍物分类。然而,传统机器学习算法的鲁棒性能和泛化能力较差,无法满足现实生活中复杂场景下应用的需要。因此,研究人员将研究重点转向了对点云数据特性的挖据上,引入降维思想将三维点云转化为深度图,借助图像中的关键点检测方法提取点云特征点。文献[9]利用三维激光雷达传感器的隐式拓扑将三维点云目标映射到二维图像上,并提出了一种基于深度直方图的移动对象半自动分割方法和引入变分图像修复方法来重建被物体遮挡的区域,实际三维激光雷达街道场景验证了该算法的有效性。
随着人工智能时代的到来,深度学习算法在目标识别任务中取得了广泛的应用和突破性的进展[10]。典型的卷积结构需要高度规则的输入数据格式,所以无序散乱点云数据首先需要转换为常规的三维体素网格或图像集合[11],这会导致数据不必要的损失,且带来额外的工作量。针对上述问题,文献[12]提出了一种三维点云目标分类和语义分割神经网络-Pointnet,该模型保证了输入点云的排列不变性,学习每个输入点对应的空间编码并通过对称函数得到全局特征,Pointnet为从目标分类到场景语义分析应用程序提供了统一的体系结构,测试效果证明该模型的有效性和优越性。
针对Pointnet网络无法获得空间点局部结构信息的问题,文中将方向卷积编码方式应用到深度卷积网络中,通过对由FPS算法选取的局部区域中心点进行3次方向编码卷积来捕获局部形状特征。同时,针对点云数据旋转性会造成目标识别结果不稳定的问题,引入空间变换网络(STN,spatial transform network)来使点云目标识别模型具有空间不变性,从而进一步提高目标识别精确度和鲁棒性。在ModelNet40、ShapeNetCore数据集上的实验结果表明了文中提出的点云目标识别方法的有效性和优越性。
1 三维点云数据特征
1.1 旋转性
在获取点云数据时,三维扫描设备的旋转会导致不同时刻采集的同一点云目标的空间坐标信息(x,y,z)发生旋转变化,如图1所示。

图1 点云旋转性
虽然图1中的(a)和(b)是相同点云,但坐标值因为经过旋转变化而发生改变,对应的卷积操作结果分别入式(1)和式(2)所示:
Ga=Conv(K,[e1,e2,e3,e4,e5])
(1)
Gb=Conv(K,[f5,f4,f3,f2,f1])
(2)
其中:G为卷积结果,e1~e5和f1~f5为输入点云的各个点的坐标信息,Conv(·)为卷积操作。
根据式(1)~(2)的计算结果,Ga≠Gb。虽然(a)和(b)是相同的点云,但是因为经过旋转,坐标发生改变,卷积结果也不同,所以卷积操作对点云的旋转变化不具有鲁棒性。文献[12]采用T-net姿态对齐网络对点云的旋转特征进行学习,但是受限于训练数据规模,以及点云旋转特征难以捕捉等问题,模型效果还有待提高。因此,文中提出一种空间变换网络来更好地解决点云旋转性问题。
1.2 排列不变性
三维点云通常呈无规则随机分布,且点与点之间没有顺序之分,具有排列不变性,每一组点云数据可以有N!(N为点数)种排列方式,即相同的点云可以有N!种矩阵表示,如图2所示。

图2 点云排列不变性
图2中, (a)和(b)是相同的点云数据,但矩阵表示不同。假设分别对(a)、(b)中的点云数据进行卷积操作,如式(3)~(4)所示:
Ga=Conv(K,[f1,f2,f3,f4,f5])
(3)
Gb=Conv(K,[f5,f4,f3,f2,f1])
(4)
其中:G为卷积结果,f1~f5为输入点云的各个点的坐标信息,Conv(·)为卷积操作。
根据式(3)~(4)的计算结果,Ga≠Gb。虽然(a)和(b)是相同的点云数据,但是因为矩阵表示不同,卷积结果也不相等,所以卷积操作无法保证点云的排列不变性。因此,将点云数据直接输入到传统卷积神经网络的进行学习的方法存在困难。为了解决上述问题,文中采用max-pooling池化操作解决点云数据排列不变性问题。
2 三维点云目标识别模型
2.1 空间变换网络(STN)
为了使三维点云目标识别模型具有空间不变性,即对于发生旋转变换的点云输入,模型仍能够对其正确进行分类,本文采用空间变换网络(STN,spatial transform networks)来自适应三维点云的旋转变换,将数据进行空间变换和对齐[13]。STN由本地化网络(Localisation network)、网格生成器(grid generator)及采样器(sampler)3个部分构成,如图3所示。

图3 STN 结构
本地化网络以feature map或者是点云数据为输入,输出为空间变换所需的参数θ,变换矩阵可以为任意形式。网格生成器通过θ和定义的空间变换方式得出输出V与输入U的映射T(θ),即实现点云坐标的对应关系,如式(5)所示:
(5)

输出V的所有坐标点是先定义好的,根据Aθ和V中每个坐标就可以计算出输入U的坐标,为了使求得的U中的坐标为整数,利用双线性差值法进行取值,采样器根据该坐标点获取到U中的特征,并将其填充到输出V中,如式(6)所示:
(6)
STN可用于输入层,也可插入到卷积层或者其它层的后面,不需要改变原 CNN模型的内部结构[14]。
2.2 深度卷积点云特征提取网络
将STN应用到传统的深度卷积神经网络中,以避免三维点云旋转性造成的网络识别结果不稳定,并采用max-pooling差异化对称函数来解决因点云数据排列不变性导致的点云数据无法
直接输入到传统CNN网络的问题,搭建的深度CNN点云特征提取网络入图4所示。

图4 点云特征提取网络结构
网络中重复的mlp是通过共享权重的卷积实现的,第一层是1×3卷积核(对应三维坐标输入),之后都是1×1大小的卷积核。经过两个空间变换网络和两个mlp之后,将原始输入的三维特征映射到高维空间,通过max-pooling层得到1×1 024的全局特征。最后经过全连接层得到k个score,连接Softmax输出层得到分类结果。
针对图4中点云特征提取网络无法提取点云局部拓扑特征的问题,引入了方向卷积编码方法,如图5所示。

图5 点云局部特征提取网络
首先,采用FPS采样方法[15]选取局部区域中心点,具体过程为:先随机选择一个点,再以离此点最远的点为起点继续迭代,直至获得需要的点数,该方法相比随机采样能够更完整得通过区域中心点采样到全局点云。
然后,对中心点分别沿X,Y和Z轴3个方向进行3级编码卷积来捕获局部形状特征,将中心点的特征放入张量M∈R2×2×2×d,三阶段定向卷积如式(7)~(9)所示:
M1=g[Convx(Ax,M) ]∈R2×2×d
(7)
M2=g[Convy(Ay,M1) ]∈R2×d
(8)
M3=g[Convz(Az,M2) ]∈R1×d
(9)
Ax,Ay,Az是要优化的卷积权重,Convx,Convy和Convz是沿X,Y和Z轴方向的卷积,g是激活函数。经过方向编码卷积后,每个点被表示为能够以方向编码方式表示中心点周围的形状图案的d维度的矢量。
2.3 点云目标分类
Softmax回归是逻辑函数在多类分类问题上的推广[16],其可以将一个含任意实数的K维向量映射到到另一个K维实向量中,并保证向量中每个元素值都在 (0,1) 之间且所有元素的和为1。文中采用Softmax回归函数对上一节深度卷积网络提取的全局特征进行处理,得到每一个类别的概率值,如图6所示。

图6 点云目标分类结构
对于给定样本,Softmax回归预测的是属于某一类别的概率如式(10)所示:
(10)
其中:x为样本,c是类别,wc是第c类的权重向量。
3 试验结果与分析
实验的硬件环境为Intel Xeon W-2123处理器,Tesla v100 32G显存显卡。
3.1 三维点云目标识别
实验使用ModelNet40[17]和ShapeNetCore[18]两个形状分类基准数据集来验证模型的性能。ModelNet40数据集是由40类人造目标产生的12 311个数据样本组成,该数据集将其中9 843个数据模型作为训练集,剩余2 468个数据作为测试集。而ShapeNetCore数据集更为丰富,有高达51 300数据样本总数,分为55个类别,数据集按70%/10%/20%的比例划分为训练机、验证集和测试集。
网络模型叠加不同区域的局部特征获得的全局特征可进一步用于目标识别,如图5网络结构所示。 在网格表面区域均匀的选取1 000个点,将每个点的空间坐标归一化后输入到网络模型中,同时为了提高模型的泛化能力,采用数据增强[19]的方法,对点云数据绕Z轴随机旋转一定角度,并在每个点的空间坐标加上均值为0标准差为0.02的高斯噪声。
在相同数据集上使用基于体素化、多视角二维图像的传统点云数据处理方法,以及PointNet基准点云处理卷积网络来和文中提出的直接输入数据的三维点云目标识别模型作对比,得到的结果如表1和表2所示。

表1 不同模型在ModelNet40上的目标分类效果比较

表2 不同模型在ShapeNetCore上的目标分类效果比较
从表1~2可以看出,文中提出的点云识别模型相比于基于体素的方法与基准点云模型取得了最佳准确率,文中所提点云卷积网络模型直接采用点云数据输入,避免了复杂的手工提取特征过程。相比于点云基准网络PointNet,文中所提模型加入了方向卷积编码模块具备利用点云局部特征的能力,在两个数据集上准确率分别提升了1.2%、1.4%。
3.2 网络模型结构验证分析
三维点云目标经过刚性旋转后的坐标信息将发生改变,为了克服点云目标旋转所造成的识别结果不稳定,在已有的深度卷积网络结构中引入STN方法来自适应的将数据进行空间变换和对齐,和其它对无序点云输入数据处理方法在ModelNet40数据集上进行对比,结果如表3所示。

表3 STN网络对模型准确率的影响
从表3中可以看出,在输入层之后加入STN之后,模型的识别率提高了1.3%。此外,对STN加入正则化约束以后,识别率进一步提高了0.4%。本次实验输入的点云数据仅包含(x,y,z)三维坐标信息,在处理更高维的点云输入数据(如包含RGB颜色信息)时,采用正则化约束的识别效果将有更大的提升。
由于实际采集的点云数据的点云位置信息易受到腐蚀,部分点云数据会产生丢失,从而造成点云密度分布不均,因此需要进一步验证文中所提模型对采样数据的鲁棒性。在ModelNet40数据集上测试不同实验条件下的分类精确度,如图7所示。实验条件为随机删除一定比例的采样点数。
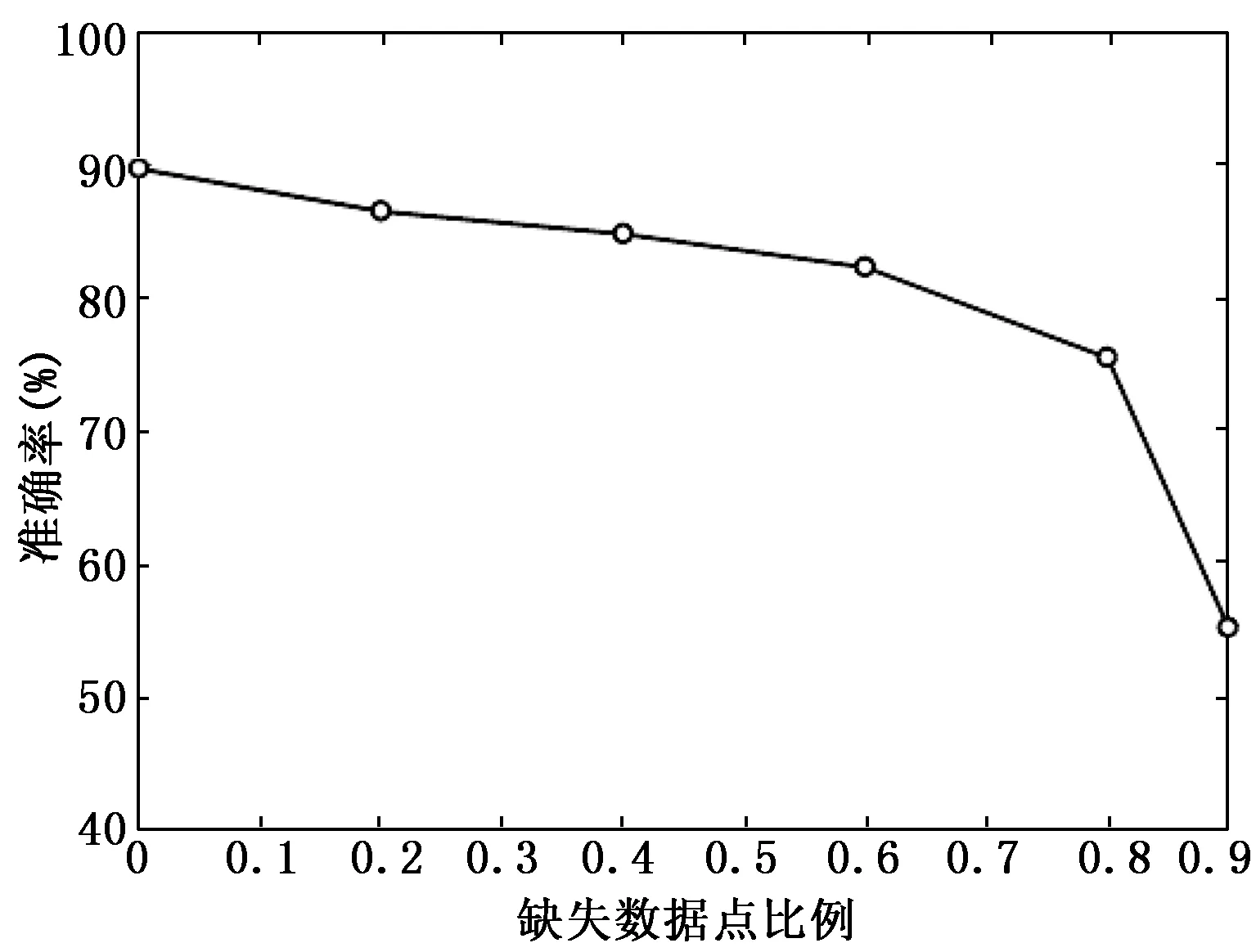
图7 不同数据缺失比例下的识别率变化
从图7可以看出,在60%采样点丢失的情况下,文中所提模型分类准确率仅下降了7.4%,实验结果表明了点云方向编码卷积网络模型在处理输入数据缺失和不均匀时有较强的鲁棒性。
3.3 网络模型可视化
深度卷积点云目标识别网络实质上将输入的低维特征(N*3)映射到高维特征(N*1 024),再采取对称函数(max-pooling)来综合得到全局特征,整个网络结构如图5所示。为便于分析,将进入对称函数前一层的特征进行可视化,具体做法是标注在每个维度上取最大值的点云数据点坐标,得到这些标注的关键点坐标与原始点云目标如图8所示。

图8 输入点云目标(左)与网络模型提取的关键点(右)对比图
所标注的关键点决定了最后网络输出的全局特征,从图8中可以看出它们描绘了一个点云目标的大致骨架结构,这样意味着即使一些非关键点数据的缺失也不会影响到网络的最终判断,也证明文中提出的卷积点云目标识别网络的鲁棒性。
4 结束语
鉴于已有的深度卷积点云目标识别模型无法有效提取点云局部拓扑特征,文中通过FPS算法选取局部区域中心点,并对中心点进行3次方向编码卷积来捕获点云目标局部形状特征。同时,采用空间变换网络来解决因点云数据旋转性会造成导致的目标识别结果不稳定问题,进一步提高了目标识别精确度和鲁棒性。文中提出的点云目标识别方法有效提高了识别精度,相较于PointNet在ModelNet40和ShapeNetCore两个数据集分别提高1.2%和1.4%。
