基于遗传算法求解一类分数阶扩散方程反问题
2022-03-29邱中龙胡彬王泽文
邱中龙,胡彬,王泽文
(东华理工大学 理学院,江西 南昌 330013)
众所周知,分数阶扩散方程已成功应用于许多反常扩散物理现象的建模中[1-3]。为了更好地对反常扩散物理现象建模,多分数阶项的时间扩散方程被提出来,一些学者对之进行了细致研究[4-7]。设Ω是空间ℝd中具有光滑边界∂Ω的有界开区域(1≤d≤3),为Ω的闭包,并设T>0,本文考虑如下多时间分数阶项的扩散方程:
其中u=u(x,t)为某种物理量在空间x点t时刻的分布,q1,q2,…,qS是正常数,β1,β2,…,βS是时间分数阶阶数且满足:
定解问题(1)中的时间分数阶均指卡普托(Caputo)型分数阶导数,即:
同时,设aij(x)∈C1()和c(x)∈C(),且c(x)≤0,以及存在常数μ>0,使得:
这里C()表示在上连续的函数全体,C1()表示在上具有一阶连续导数的函数全体。
现实物理世界中,扩散方程中分数阶阶数βs、常数系数qs以及反应系数C(x)可能是未知的,需要通过附加的测量数据来确定它们,这就是分数阶扩散方程反问题需要研究的内容之一。文献[8]研究了识别多分数阶阶数的反问题,在已知分数阶个数的前提下,作者利用边界内部某个点的测量数据,通过同伦正则化算法识别多分数阶的阶数。文献[9]考虑了在时间分数阶扩散方程中同时重建空间源项和分数阶阶数的反问题,在不同的观测数据下,分别证明了一维和二维情形下反问题解的唯一性,构造了一种交替最小化的数值反演算法。
本文主要考虑以下两个反问题:
反问题I: 假设q1,q2,...,qS,aij(x),c(x)和u0(x)均已知,且分数阶项数S已知,由数据u(x0,t),t∈I⊆[0,T]识别分数阶阶数β1,β2,…,βS;
反问题II: 假设aij(x)和u0(x)均已知,分数阶项数S已知,由附加数据u(x0,t),t∈I⊆[0,T],重建q1,q2,...,qS和β1,β2,…,βS。
上述反问题的唯一性已在文献[5]中得到证明,在此以下述引理形式给出该结论:
引理1设d=1时有u0(x)∈C()和2≤d≤3时有u0(x)∈C1()。u是定解问题(1)的解,v是下述定解问题:
其中aij(x)∈C1()且满足(5)、c(x)∈C()且c(x)≤0。对于给定x0∈Ω,若u(x0,t)=v(x0,t),t∈I,则有βs =αs,qs=rs,s=1,2,…,S。
对于应用遗传算法求解非线性问题,已经有些学者进行了研究。文献[10]将爬山算法和传统遗传算法相结合,提出一种求解非线性方程组的改进遗传算法。文献[11]为了优化传统多址通信信道编码的效率以及误码率,提出基于遗传算法的多址通信信道编码优化方法。文献[12]基于最大熵法引入拉格朗日乘子构建样本可能的概率密度函数,而后将拉格朗日乘子的求解转化为最小值优化问题,并利用遗传算法的寻优功能搜索问题的全局最优解,从而得出了最大熵法与遗传算法在确定数据概率密度函数中的有效性和可行性。文献[13]将无功优化规划可归结为非线性的条件组合优化问题,然后利用遗传算法进行求解,但其在遗传算法的基础上对一些环节做出相应的改进,利用灵敏度加强算法的交叉、变异性,使得遗传算法在求取全局最优解时有着更好的表现,进而使得算法整体的效率得到提升。
对于时间分数阶扩散方程反问题,文献[14]考虑了由柯西(Cauchy)数据重建方程中的分数阶阶数和零阶项系数的反问题。文献[15]研究了一类同时重建分数阶阶数和初始分布的反问题,证明了反问题的解是唯一的。本文考虑一类多个时间分数阶项的扩散方程反问题,将识别分数阶阶数及其系数转化为优化问题,然后利用遗传算法求解该优化问题,算法过程中正问题的解法与文献[8][16]类似。本文接下来的安排如下:第二小节将反问题建模为优化问题并给出基于遗传算法的求解方案;第三小节介绍了如何利用精确数据和噪声数据对反问题进行数值模拟;第四小节给出结论。
1 基于遗传算法的数值反演方案
1.1 反问题的建模
记m(t)=u(x0,t),t∈I⊆[0,T]。设m(t)测量数据为mδ(t),满足:
其中δ是误差水平。记f =(β1,β2,…,βS)T或者f=(β1,β2,…,βS,q1,q2,…,qS)T,并记对应于f的正问题的解(1)为u(f)(x0,t)。于是,可将反问题归结为极小化泛函:
在极小化问题(7)中,u(f)(x0,t)通过有限差分方法计算得到。接下来,我们以Ω =(0,l)为例说明正问题的有限差分方法,并记此时的aij(x)为D(x),且D(x)∈C1[0,l]和D(x)>0,x∈[0,l]。
首先,将区域[0,l]×[0,T]划分为M×N网格,其上的网格点为(xm,tn),且xm=mh(m=0,1,…,M),tn=nτ(n=0,1,…,N),其中空间步长,时间步长,网格比为。记,Dm=D(xm),cm=c(xm)。
然后,根据分数阶导数的定义(3),可将其直接离散为:
对于(1)中第一个方程的右端,采用具有二阶精度的数值微分公式离散为:
最后,在(8)(9)两式中舍去高阶小量,即得到(1)中第一个方程的有限差分格式:
即为:
对于m=1,2,…,M-1,将上式简记为:
其中:
至此,得到了计算u(f)(x0,t)的有限差分格式(11)。
其中B =b[ij]M-1×M-1,且:
1.2 基于遗传算法的求解方案
遗传算法(Genetic Algorith m)最早是由美国的约翰·霍兰德(John holland)于20世纪70年代提出的,该算法是根据大自然中生物体进化规律而设计的,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。遗传算法已被人们广泛地应用于组合优化、机器学习以及信号处理等领域。
对于反问题I,将待识别的分数阶阶数βs(s=1,2,…,S)记作向量f=(β1,β2,…,βS)T。根据反问题I的假设条件,构建如下约束条件:
其中:
对于反问题II,我们将分数阶阶数βs(s =1,2,…,S)和分数阶项的组合系数记作向量f =(β1,β2,…,βS,q1,q2,…,qS)T。显然,向量f满足约束条件:
其中:
因为本文采用有限差分格式计算得到u(f)(x0,tj),所以遗传算法中的适应度函数实际上是(7)中泛函的离散形式,其中的积分由梯形公式近似得到:
其中tj是区间I的N等分点。在确定约束条件和适应度函数后,即可建立反问题的遗传算法求解方案,其中遗传算法的计算步骤如图1所示:

图1 遗传算法计算步骤图
2 数值模拟
本文仅就以下定解问题:
进行数值模拟,从而说明基于遗传算法的数值反演方案在一定程度上是可行的。数值模拟中,我们始终取T=1,测量数据始终取u(,t),t∈[0.3,1.0],正问题计算中始终取网格步长。误差数据按以下方式获得:
其中r(t)是[-1,1]上服从正态分布的一个随机数,δ是相对误差水平。接下来的数值模拟中,我们始终用f表示反演问题的精确解,而用finv表示反演解,他们之间的相对误差定义为。
2.1 反问题I的数值模拟
为简单起见,取q1=q2=…=qS=1,f=(β1,β2,…,βS)T。在遗传算法中,设置种群大小为100,交叉概率为0.8,变异概率为0.1。运行10次取平均的计算结果见表1和表2。

表1 相对误差δ =0时分数阶阶数的反演结果

表2 相对误差δ =3%时分数阶阶数的反演结果
2.2 反问题II的数值模拟
在反问题II 中,分数阶阶数β1,β2,…,βS、系数q1,q2,…,qS均未知,记待识别参数变量为f =(β1,β2,…,βS,q1,q2,…,qS)T。在遗传算法中,种群大小取为100,交叉概率为0.8,变异概率为0.1。运行10次取平均的计算结果见表3和表4。
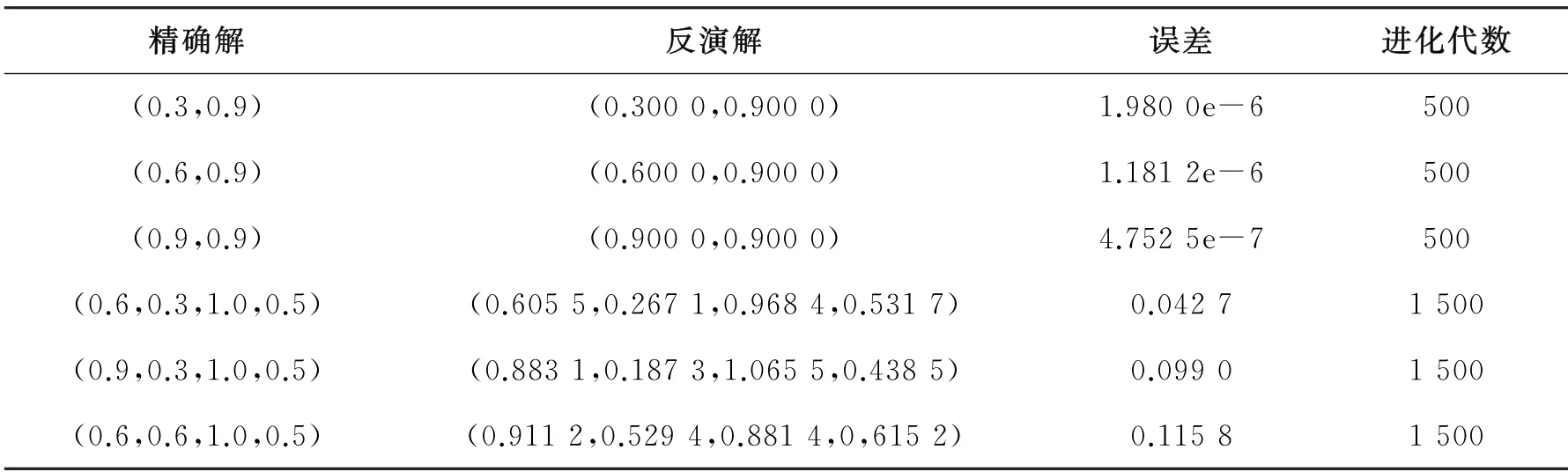
表3 相对误差δ =0时分数阶阶数和系数的反演结果
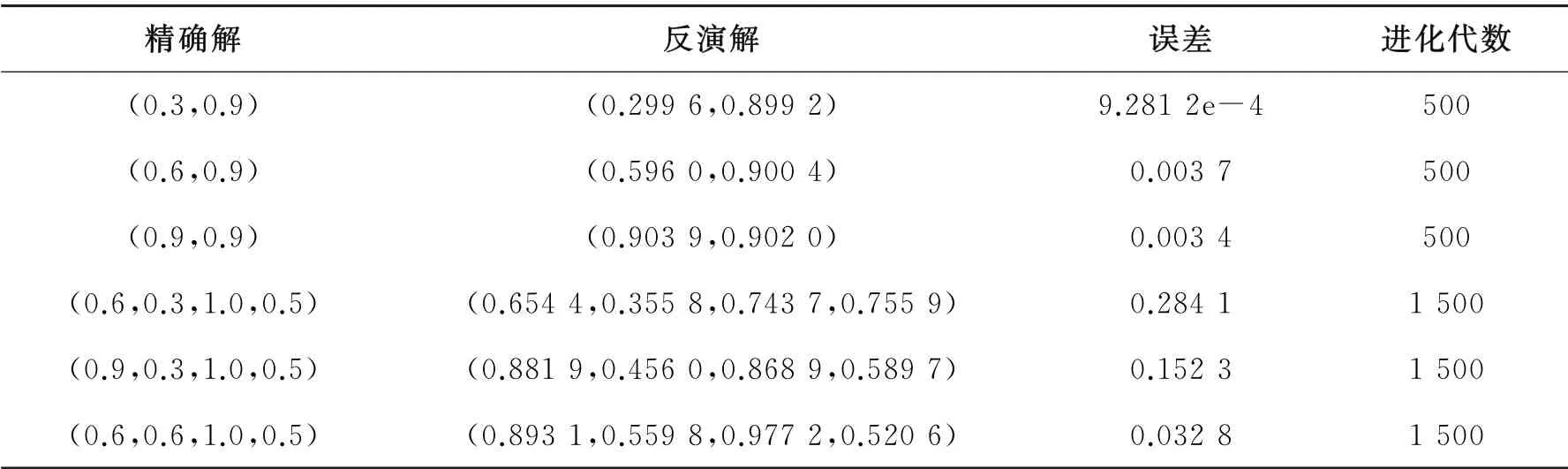
表4 相对误差δ =3%时分数阶阶数和系数的反演结果
3 结论
本文利用空间域内的测量结果,研究了分数阶扩散方程中的两个反问题。在已知反演问题是唯一的情况下,给出基于遗传算法的求解方案后,利用遗传算法进行了精确数据的和随机噪声数据的数值反演模拟。通过数值模拟的结果,可以看出:在只有两个参数待识别时,反问题I和反问题II均具有很好的反演效果,特别是基于精确数据的反演结果非常好;当待识别的参数个数增多后,反演效果就差强人意了,但是所得结果已经靠近真值,故可以作为其他方法的迭代初值。因此,当待识别的分数阶阶数和其组合系数的个数比较多时,如何有效地重建这些参数是需要继续深入研究的。
