分布数据缺失的最优传输研究*
2022-03-29阮一鸣杨建斌
阮一鸣, 杨建斌
(河海大学 理学院,江苏 南京 211100)
1 引言
最优传输本质是刻画分布与分布之间的最优距离,在图像处理、机器学习和经济学等各个方面都有应用[1-7]. 在实践中受各种因素的影响,获取的分布数据会出现缺失的情形,例如在图像处理领域,图像在存储过程中由于硬件或软件的原因会造成像素或灰度值缺失等,此时利用最优传输理论及其模型会出现求解较为困难且计算结果误差较大的问题.如何在数据缺失情形下得到最优传输问题的相应结果,同时求解估算缺失的数据,是最优传输领域中的一个关键问题.
相对于给定的代价函数,最优传输问题则是寻求把一种分布转化为另一种分布的最有效的方式,其主要可分为蒙日(Monge)问题和康塔洛维奇(Kantorovich)问题. 其中蒙日型最优传输问题的一般形式如下:
考虑X和Y是完备可分的度量空间,给定概率测度μ∈P(X),v∈P(Y),其中P(X)和P(Y)代表X和Y上所有概率测度所构成的空间,给定代价函数c(x,y)∶X×Y→[0,+∞),蒙日型最优传输问题则是求解
(1)
T#μ=v为约束条件,T为一个推前算子,由映射T诱导的推前测度T#μ定义为(T#μ)(A)∶=μ(T-1(A)),其中A⊂Y是任意可测集合. 由于空间∑(μ,v)∶={T∶X→Y|T#μ=v}在弱收敛下不是封闭的,这导致了求解蒙日型最优传输问题的内在困难性[8].
康塔洛维奇则将蒙日问题中的传输映射松弛成传输方案,即转换为联合概率分布γ(x,y)∈P(X×Y),其边际概率分布分别为μ(x)和v(y),即满足
(2)
给定两个概率测度μ∈P(X)和v∈P(Y)以及相应的代价函数c(x,y)∶X×Y→[0,+∞),其中X和Y是完备可分的度量空间,则康塔洛维奇型最优传输问题则是求解
(3)
其中联合概率测度γ属于传输方案空间
(4)
考虑(X,d)为完备可分的度量空间,P(X)为度量空间(X,d)上所有概率测度构成的空间,对任意概率测度μ、v∈P(X),μ和v的s阶Wasserstein距离定义为
(5)
其中,s∈[1,+∞),Π(μ,v)为对应上述的传输方案空间.当s=1时,W(μ,v)称为EMD距离(Earth Mover′s distance),即推土机距离或陆地移动距离.康塔洛维奇问题解除完全确定性传输的限制[4],其模型更简捷有效,因此在实际中具有更为广泛的应用与研究.
近年来,对于最优传输问题的求解也逐渐成为优化领域的一个热点.但从匈牙利算法[9]和拍卖算法[10]到经典的线性规划算法[11],均存在较高的时间复杂度,对于大规模的问题仍具有较大的局限性,而熵正则化算法[12-13]的提出则加速了最优传输问题的计算求解.本文在模型中加入熵正则项来平滑数据缺失的最优传输问题,提出了一种求解数据缺失情形下的最优传输问题的熵正则化算法,同时将其应用于运输问题与图像检索问题,并给出相应的实例,数值算例表明了算法对于求解数据缺失的最优传输问题的有效性.
2 数据缺失的最优传输问题
2.1 离散最优传输问题
考虑如下两个离散分布:
(6)

给定相应的代价矩阵C=(cij)∈Rn×m,则离散最优传输问题可描述为
(7)
其中,W(μ,v)即EMD距离,γ为耦合矩阵,γij=γ(xi,yj)为传输方案,表示从xi运输到yj的质量,cij=c(xi,yj)表示xi运输到yj所花费的代价.pi=p(xi)和qj=q(yj)分别代表分布数据xi和yj所对应的概率权重向量.则问题(7)所对应的优化模型可表示为
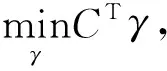
(8)
其中

b=.
2.2 分布数据缺失的最优传输问题

假定离散分布μ对应的点云数据已知,分布v对应的点云数据有k个数据缺失,设缺失的数据为y1,y2,…yk,且其所对应的概率权重向量为q1,q2,…qk,此时与经典的最优传输问题相比,目标分布增加了k个自由度,需同时考虑最优传输方案γ以及对应缺失的数据y1,y2,…yk.与问题(7)相比,增加了k个未知量,则此问题可表述为
(9)
则问题(9)所对应的优化模型可表示为
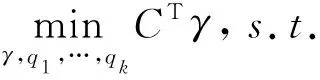
(10)
其中,
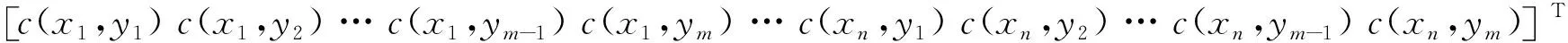
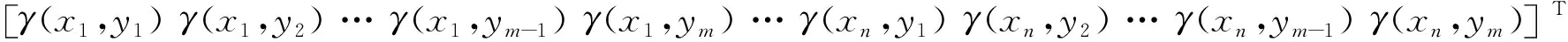

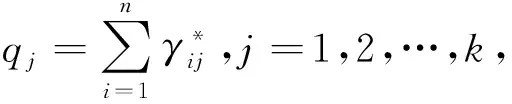
3 数据缺失情形下的最优传输的求解算法
3.1 熵正则化
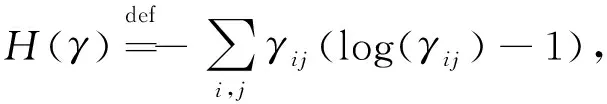
(11)
其中,ε表示正则化系数,此时的近似最优传输问题便成为ε-强凸函数,故其具有唯一解.
3.2 数据缺失情形下的最优传输的求解算法
对于问题(11),可将其等价地转化为相应的投影问题,且投影度量为KL散度[13],定义为
(12)
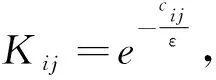
(13)
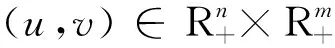
γ=diag(u)Kdiag(v),
(14)
从而可得本文算法.

1:l=0,v(0)=1m
2:whilel 3:u(l+1)=p./Kv(l) 4:A=KTu(l+1) 8:l=l+1 9:end while 考虑若干个货物从仓库运到工厂,其中X=(x1,x2,…,xn-1,xn)代表n个工厂,工厂xi的需求量为wxi,Y=(y1,y2,…,ym)代表m个仓库,仓库yj的储存量为wyj,货物从工厂xi运送至仓库yj的代价为cij=c(xi,yj).若工厂的需求量WX=(wx1,…,wxn-1,wxn)已知,仓库储存量WY=(wy1,wy2…,wym-1,wym)有部分数据wy1,wy2…,wyk未知,此时运输问题可表示为基于问题(9)的最优传输问题,即 (15) 其中γij=γ(xi,yj)代表相应的传输方案.下面给出一个实例. 其中缺失的数据[wy1,wy2…,wy4]=[107.049 4,18.958 0,19.017 2,159.975 4]. 图像检索,本质用一个图片去和数据集中的图片一一匹配,从而检索出满足条件的图片.在2000年Rubner[16]提出EMD距离的定义并将其应用于图像检索领域.基于最优传输理论,图像检索通常分为两步,首先提取图像的特征从而得到一个高维的直方图或向量来表示图像;其次计算两幅图像的特征间的EMD距离来度量图像特征间的相似度.以上方法对于图像数据未缺失的情形具有较好的效果,若待检索图片即目标图片存在部分未知(即图像特征存在未知或缺失),此时利用上述方法进行处理则较为困难. 考虑图像为灰度图像,对于给定的灰度图像则其对应的直方图在中的离散分布满足(6)式.在离散意义下,图像可看成从图像中提取的特征直方图,此时若两幅图像直方图的组数分别为N和M,直方图之间的传输可用N×M的联合概率矩阵γ表示,其中γij=γ(xi,yj)代表对应位置所传输的质量.假定目标图片分布直方图部分缺失即对应图像特征或灰度值有所缺失,检索数据集图片直方图未缺失.给定两张图片P和Q,其中P为检索数据集中图片,Q为目标图片,则P和Q特征可用灰度直方图描述.其特征集合:P={(p1,wp1),(p2,wp2),…,(pn,wpn)},Q={(q1,wq1),(q2,wq2),…,(qm,wqm)},其中pi是检索数据集中图片的第i个特征,qj是目标图片的第j个特征,wpi是特征pi的权重,即其对应直方图块值,设目标图片特征wqk+1,…,wqm缺失,代价矩阵cij=‖pi-qj‖2.给定分布直方图缺失的目标图片与检索数据库中的图片,两张图片的相似程度则可用EMD距离来衡量,即此图像特征缺失的图像检索问题可转换为基于问题(9)的最优传输问题,即 (16) 基于上述理论以及本文算法,需求解图片直方图之间的最优传输方案γ从而求出图片间的EMD距离. 下面给出一个实例.选取10张256*256图片构成检索数据集,选取图片特征数量为50,即直方图块数量为50,目标图片为灰度值缺失图像,特征有20个缺失,其中目标图片直方图及其缺失部分与对应特征缺失的目标图片见图1,图片黑色部分为图像特征缺失部分,检索数据集见图2. 图1 目标图片特征分布直方图、特征缺失的目标图片 图2 检索数据集图片 设定目标图片为图片0,检索数据集图片为图片1-10,分别计算图片0与数据集图片1-10之间的EMD距离见表1. 表1 目标图片与数据集图片特征分布的距离(20特征缺失) 从表1得到,目标图片与图片3的EMD距离为0.008 5,小于与其他图片的EMD距离,即目标图片与图片3最为相似,也与先验保持一致. 探究了分布数据缺失情形下的最优传输问题,给出其基本理论以及对应优化模型,针对模型的较大稀疏性,在问题中加入熵正则项来平滑数据缺失情形下的最优传输问题,从而提出了一种数据缺失情形下的最优传输的熵正则化算法,将其应用于运输问题以及图像检索问题,结果验证了模型及算法的有效性.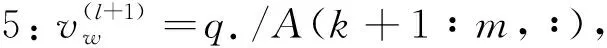
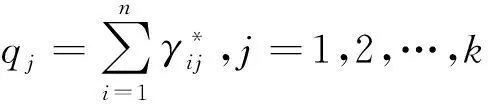
4 实际应用
4.1 基于运输问题的应用


4.2 基于图像检索问题的应用



5 结语
