乡村公路管理养护效能考核方法及应用
2022-03-29钱圣隆
钱圣隆
(南通市公路事业发展中心如东分中心,江苏 南通 226400)
在乡村公路管养考核中,需要对各镇管养的路段进行评价,涵盖安全性、舒适性等各方面要求。在近年来推进的“四好农路”工作中,乡镇管养效能也成为考核评价管养工作中极为重要的一环,关系到各项工作能否落到实处、关系到交通参与者能否享受到“四好农路”创建过程中带来的制度红利,管养工作提质增效也是交通强国带动区域经济发展的重要手段之一。
但在实际工作中,对于乡村公路管养考核仅采用单项扣减分数的做法,在对各条长短差距较大的路段进行打分时,常常出现里程较长的路段整体较好但零散扣分项较多,里程较短的路段管养极差但总扣分项不多。同时,在对于不同扣分项权衡时,缺乏统一标准,以此造成评价过程中主观因素影响极大,在一定程度上未能反映出真实管养效能。因此,在理论上统一乡村公路管养评价标准,建立统一的指标体系并用于实际检查考核中就显得尤为重要。
1 模型建立
为了能够利用层次分析法对各路段管养情况进行评价,需建立起被评价系统的层次结构模型,建模过程如下:
1.1 明确评价目的
评价目的是对各路段管养情况、病害数量等进行综合评价,并进行排序,供决策者使用。
1.2 提出评价对象
常见农村公路管理养护问题有很多,本文一方面将常见问题、病害进行梳理归纳,另一方面将各类相似的问题进行了整合,尽量减少数据分析难度,最终形成常见的问题、病害清单。
1.3 确定评价准则
当前,随着“四好农村路”创建工作不断推进,乡村公路建管养运的内涵也随之不断深化、提升。传统乡村公路的通行要求已不能满足时代的需要,对于乡村公路管养考核不能只满足于通达,还应不断提升来满足日益增长的人民群众的需要。故本文将乡村公路管养评价指标根据是否影响交通安全正常通行、是否有较大隐患或影响应急响应、影响当季工作重点、影响路域环境整洁美观等方面对各类病害及问题的重要性进行评价。
1.4 建立系统的层次结构模型
根据评价对象和评价准则,可以构建含16个要素的结构模型,见表1。根据评价要求,可建立起该系统的层次结构模型,见表1。

表1 常见病害、问题的结构模型
2 建立判断矩阵并计算优先级向量
(1)先以路线管养效能为基准,对准则层建立判断矩阵,见表2。之后,需计算其矩阵特征值并核实数据一致性,如病害评价矩阵其特征值及一致性为:[0.181 4、0.020 2、0.058 2、0.085 9、0.141 3、0.141 3、0.010 4、0.010 4、0.0432、0.085 9、0.085 9、0.0582、0.020 2、0.0142、0.014 2、0.028 9]。CI=0.0621,CR=0.0387,一致性可接受。

表2 层次分析法判断矩阵
(2)再以准则层为依据,对方案层要素建立判断矩阵。下面对某镇检查考核问题汇总,见表3。

表3 某镇检查考核问题汇总(部分)
首先,需根据不同路段里程折算病害/问题,将不同问题数量划定不同评定等级,据此形成路线对比矩阵。由于此时有16个准则,故有16个判断矩阵,在此仅列出部分,见表4。
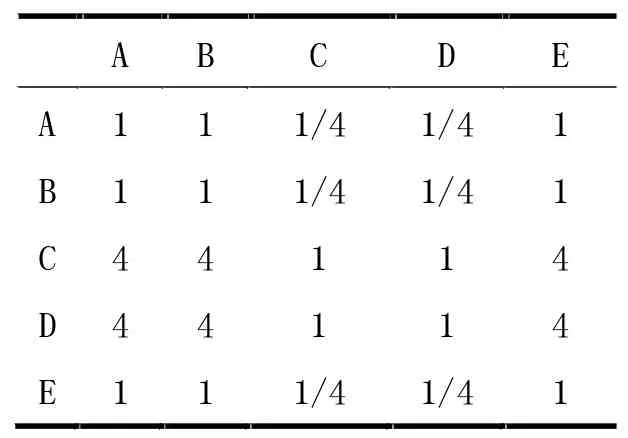
表4 各路线坑塘评价矩阵
数据特征值:[0.116 4,0.116 4,0.325 4,0.325 4,0.116 4],CI=-0.034 3,CR=-0.029 9,数据一致性可接受。
(3)确定总体优先级。根据上文所计算出的特征值,可计算五条路线对各病害的权重为,见表5。
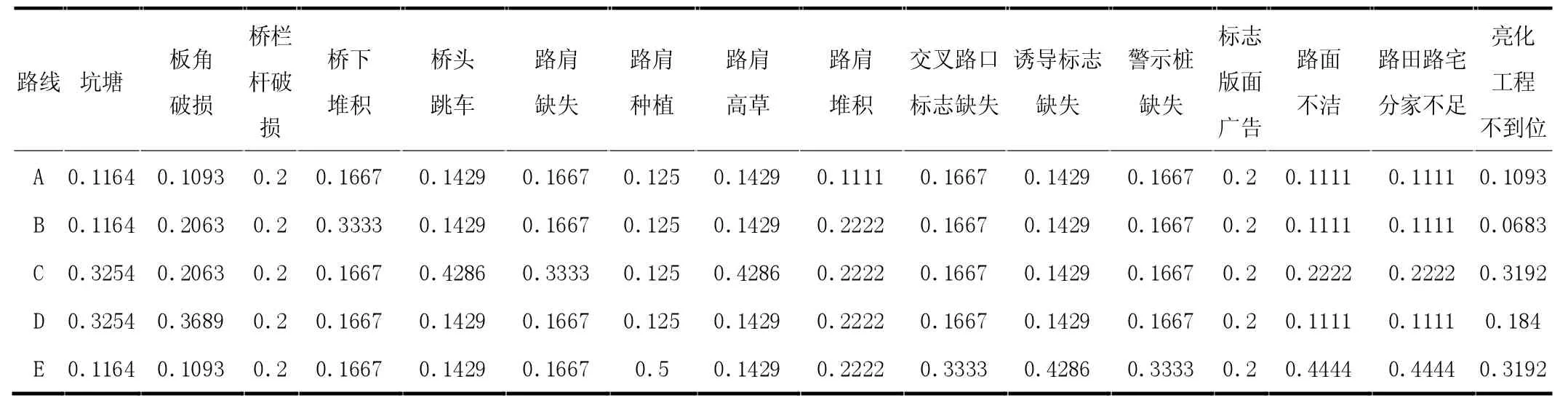
表5 各条路线病害、问题相对权重
结合路线管养效能判断矩阵的特征值可得出总体优先级,见表6。
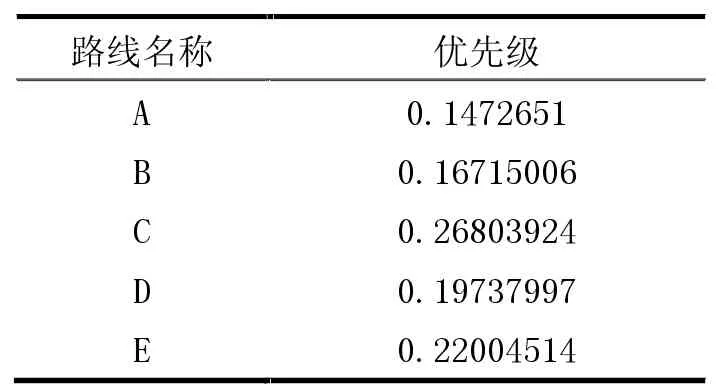
表6 各路线总体优先级
根据总体优先级向量,5条路线的管养排序情况为(从优至差):A>B>D>E>C,与主观评价相同。
3 应用要点
本文中针对不同路段的管理养护效能进行考核评价,可以看出在应用层次分析法评价道路管养效能时,需注意如下几点:
(1)正确建立层次模型
因为层次分析法是以系统的层次结构模型为基础进行数据分析的,因此必须要求在计算时保证层次结构模型正确建立,在此基础上才能得到正确、可行的结论。
(2)判断矩阵一致性检验
由于判断矩阵在建立时,仅考虑两两对比得出结论,这种方法一方面便于评价指标的建立,但也因此存在一定偏差风险。仅当判断矩阵一致性较好时,该矩阵才可用。因此一般采用计算判断矩阵的最大特征值来进行检验。
(3)合理划分评价等级
在建立不同问题的路线对比矩阵时,由于各类问题及病害分布数量具有极大差异性,因此在针对不同问题评价时,就需要采用不同的方法进行判别。如路侧高草问题,单公里问题数量变化范围为0~1,而交通标志缺失问题,单公里问题数量变化范围可能仅为0~0.1,因此针对不同问题采用不同的评价层级才能更加合理地建立判断矩阵。
