二维椭圆零件排样问题研究

2022-03-29丛玉龙蒋兴文

科技创新与应用 2022年7期

张闯，高强，2*，丛玉龙，蒋兴文，周明

（1.沈阳工程学院，辽宁沈阳 110136；2.沈阳建筑大学机械工程学院，辽宁沈阳 110168）

在大型工业产品中，如机床、轮船及飞机常常需要很多的小零件，如螺钉、螺帽、螺栓和活塞等。在零件的生产过程中，第一步是需要依照零件产品尺寸从原材料中截取初级产品。在这道工序中，不同的截取方案具有不同的材料利用率，而原材料的利用率（原材料截取初级产品的总体积与原材料体积之比）直接影响产品的生产成本。在市场上，零件的截面（表面）形状是多种多样的，有圆形、矩形等，零件的厚度（高度）尺寸也是大小不一的。在原材料尺寸固定的前提下，截取初级产品后产生的废料最少是企业的追求。

本文以6 060 mm×2 160 mm板材加工尽可能多的横径为60 mm，竖径为40 mm的正椭圆形产品为例，探讨满足产品数量要求的整体切割方案。

1 外切矩形件直接排样

二维零件排样问题是近年来的研究热点[1]，首先将椭圆简化为外切矩形，通过紧密切割[2]（无缝隙排列）的方式建立模型，即矩形件排样优化。将原材料水平放置，以原材料左下角为坐标原点（0，0），以长边所在直线为x轴，短边所在直线为y轴，建立平面直角坐标系。但紧密切割存在横向摆放、竖向摆放两种情况如图1所示。

图1 矩形件排样

首先若将产品横向摆放，并且彼此间无缝隙紧密排列。排列到最后可能会出现横向摆放不足以摆放一块，但是竖向摆放还有余量的情况。同理竖向摆放会出现横向摆放不足以摆放一块，但是横向摆放还有余量的情况。

对于横向摆放，先采用从上往下逐排摆列摆放的方式，假设先将t1块产品紧密横放排列，t2块产品紧密竖放排列；再从下往上逐排排列摆放，将t3块产品紧密竖放排列，t4块产品紧密横放排列。n为可切割的产品数，可建立数学模型：

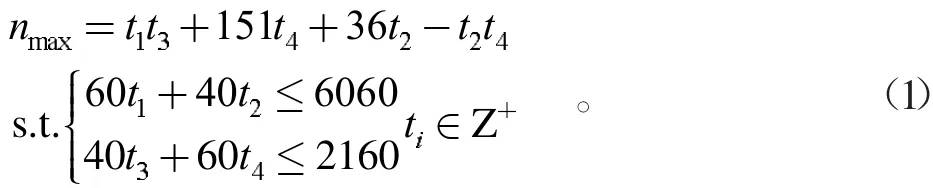
同理，对于竖向摆放，可建立数学模型：

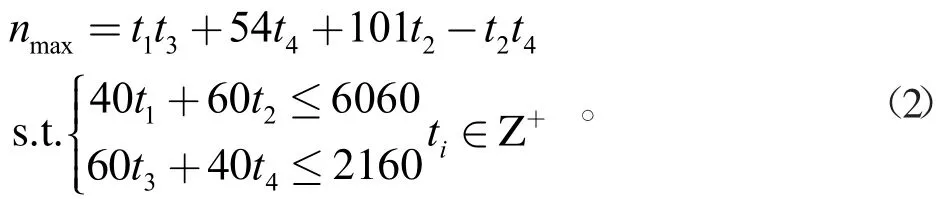
求解后结果见表1，最优结果为5 454块。

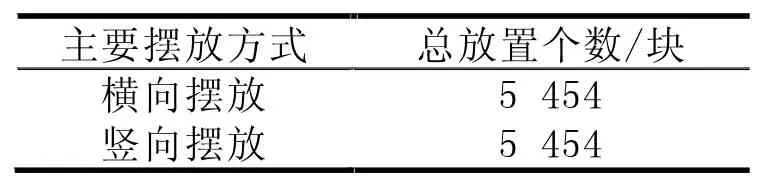
表1 矩形件排样求解结果

2 外切矩形件优化排样

由于外切矩形件直接排样在面对不同规格零件时，需要重新建立数学模型，实用性较差。故将其算法优化[3]，增强算法的实用性。

将第i块产品中心的坐标与切割方向记为（xi，yi，di），其中i=∈N*，di=±1，（xi，yi）表示第i块产品的中心坐标，di=1表示第i块产品的长边水平切割，di=-1表示第i块产品短边的水平切割。为了使原材料的利用率最大，只需总的产品所占面积最大，即可满足切割产品数目最多。

在约束条件上要确保以下三点：

（1）任意两块产品不能重合，即横坐标或纵坐标满足式（3）两种关系之一。

（2）每块产品必须要在原材料的范围内，即需要同时满足式（4）两种关系。

（3）产品的总面积必须大于等于零，且不能超过原材料面积，即需要满足式（5）的关系。

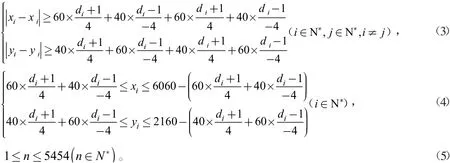
综上，该数学模型可以表示为：

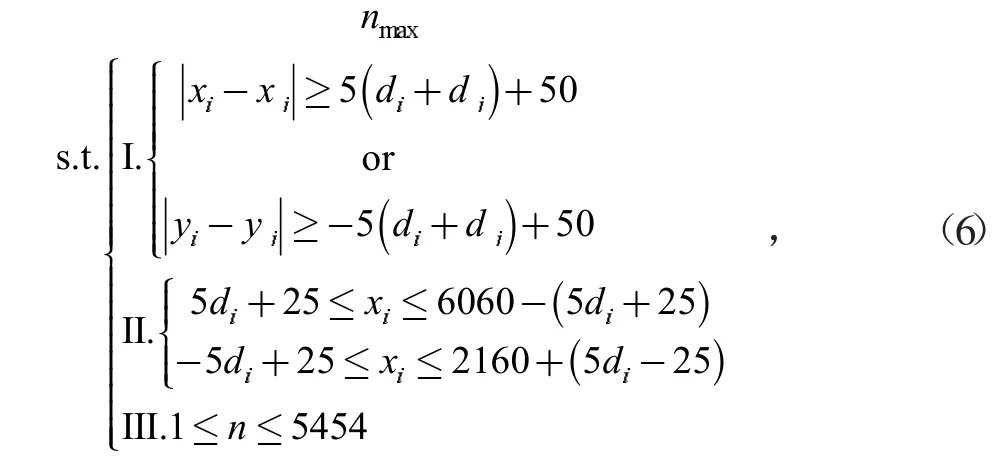
其中：i∈N*，j∈N*，i≠j，n∈N*。

求解结果为最多摆放5 454块，与外切矩形件直接排样相同，但建模与计算速度较外切矩形件直接排样更快，该模型可适用于复杂的矩形切割问题，但对于椭圆切割问题，该方法空间利用率过低，无法满足设计需求。

3 椭圆最小密排优化

上述模型通过将椭圆简化为矩形，通过矩形件排样的算法建立模型，得到了最佳的切割方式，这种模型如果是切割矩形件可以得到最优解，但是切割椭圆由于椭圆面积仅占外接矩形面积的π/4，约为78.5%，显然不是最优解。而椭圆致密的排列方式一定是要使每一个椭圆尽可能地靠近，并且是按照一定规律排列，如同理想原子的排列一样。

阿克塞尔图早在1910年就对圆形的六角密堆积进行了证明[4]，对于圆形而言，六角密堆积是最致密结构，致密度为，其排列方式如图2所示。

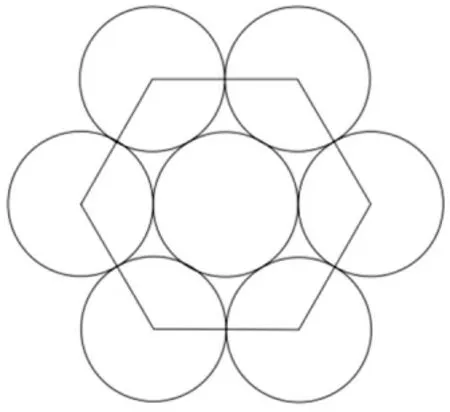
图2 六角密堆积示意图

圆的六角密堆积是平面上最有效的堆积方式，所以像椭圆这种的圆锥曲线轮廓的工件，可以根据圆的六角密堆积建立仿射坐标系[5]，将椭圆类比成圆，进行密堆积排列。再对上述算法进行优化，即可得到最优解。

对于椭圆的密堆积排列，首先建立仿射坐标系，该问题不需要建立三维仿射坐标系，在平面内建立二维仿射坐标系即可。即原坐标系内的任意一点（x，y）原本表示为r→=xι→+yJ→，现在仿射坐标系内（x′，y′）的坐标表示为r→=x'ι→+y'J→=xι→+1.5yJ→。通过坐标反变换，即可得到椭圆的密堆积排列如图3所示。