基于五维超混沌的太赫兹调制跳变性能分析

丁元明，赵佳倩，冯建新

(大连大学 通信与网络重点实验室，辽宁 大连 116622)

0 引言

太赫兹波是一种频率100 GHz～10 THz的电磁波，兼具毫米波以及红外可见光电磁波的优点，具备高频率、窄波束等特性，应用于军事以及民用通信具有更好的抗干扰性和抗截获性[1-3]。

传统抗截获方式有扩频通信和跳频通信[4-6]，利用扩频码和跳频图案的不确定设计，提高信号的抗截获性能。但是，随着通信信号处理技术和机器学习理论的发展，对于扩频和跳频信号的检测、分选、识别等技术较为成熟，采用单一调制的扩跳频通信体制难以保障安全。因此，一种系统复杂度更高的抗截获通信技术就变得很有必要[7-8]。

调制跳变技术作为一种新的加密传输方式，将通信信号的调制方式作为优化对象，通过对调制方式的跳变设计，使敌对方无源探测系统的调制识别机制失效，从而实现良好的抗截获性和较高的频谱利用率。但是，目前对于调制跳变技术的相关研究仍处于起步阶段。调制跳变技术由四川大学高勇提出[9]。刘亚擎等人[10]将调制跳变和跳频系统相结合，提出了调制方式和信号频率联合跳变的抗截获通信系统框架。马卓[11]最先提出将混沌技术应用于调制跳变，提出了基于信息熵和混沌编码的调制跳变通信方法，提高了信号的保密传输能力。邰能建等人[12]针对调制跳变系统的同步，提出了一种匹配相关双驻留并行捕获方法。刘鹏飞等人[13]在传统三维Lorenz混沌系统的基础上，提出了加权反馈三维混沌系统的调制跳变技术，得到复杂度更高跳变图案，提高了系统的抗截获能力。

由上可见，当前研究对信号传输的保密性还不能达到实际应用的要求，存在系统复杂度低、抗截获性能差亟需解决的问题。基于Logistic、Lorenz等低维混沌系统导致通信系统的复杂度低、抗截获性能差，同时，由于调制跳变系统常用于实际电子对抗场景，为确保通信系统信号的安全、稳定传输，需要采用更精确的信噪比估计算法。针对以上问题，本文基于传统的低维混沌系统，综合考虑跳变图案的不确定性和计算复杂度等因素，提出了系统复杂度更高的五维超混沌系统；根据太赫兹信号的高频率、低功率等特殊性，提出了一种基于频域的信噪比估计算法。通过仿真实验表明，在一定的计算复杂度下，本文所提的基于五维超混沌系统的太赫兹调制跳变系统可以根据信道的实时状态，自适应地选择合适的调制方式，有效提高了通信系统的抗截获性能。

1 五维超混沌系统模型

1.1 典型的三维Lorenz系统

本文以经典的三维Lorenz混沌系统为基础，系统的表达式如下[14]：

(1)

式中，x1，x2，x3为混沌系统的输入变量，其一阶导数为输出变量；a,b,c为系统参数。通过改变系统的参数，可以得到不同的Lyapunov指数。在系统中，具有一个正的Lyapunov指数，就定义其为混沌系统；具有2个或者2个以上的Lyapunov指数，就为超混沌系统。对于经典的三维Lorenz混沌系统，由于其参数较少，系统复杂度有限，被破译的风险较大。

1.2 基于三维Lorenz系统的五维超混沌系统

依据文献[15]所提的状态反馈方法，本文在传统三维Lorenz混沌系统的基础上，综合考虑系统的计算复杂度，用状态反馈方法在三维Lorenz系统中引入第四维反馈变量和第五维反馈变量，可获得一个新的五维超混沌系统如下：

(2)

式中，a,b,c,d,e是系统参数。根据式(2)进行仿真可知，当系统参数分别取值10，28，8/3，6.1，-2.8时，系统的Lyapunov指数数值趋于稳定，为λ1=3.310 9,λ2=1.283 4,λ3=0.7,λ4=-5.225 8,λ5=-5.235 1有3个值恒大于零。因此，在一定的计算复杂度下，本文所使用的五维混沌系统为超混沌系统，相比于传统的三维Lorenz混沌系统具有更高的复杂度。

1.3 五维超混沌系统的复杂度评估

近似熵(Approximate Entropy，AE)通常是一种用来对序列变化复杂程度进行评估的数学度量，一般采用序列的近似熵方法来表示其中序列变化波动的规律性以及其变化的不可预测性[16-17]。在序列中，新信息产生的概率是决定序列近似复杂程度的重要因素之一，新信息产生的概率越大，复杂度就越高，混沌性也就变得越好，那么序列AE值也就更大。

若已知序列为s(i)，其维数为N，则可通过序列s(i)产生m维向量u(i)，如下：

u(i)=[s(i),s(i+1),...,s(i+m-1)]，

(3)

式中，i=1,2,...,N-m+1。

定义向量d[u(i),u(j)]为向量u(i)的最大差值：

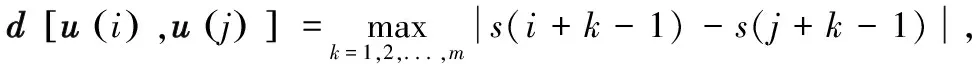
(4)

式中，j=1,2,...,N-m+1,j≠i。

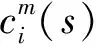
(5)

式中，num表示d[u(i),u(j)]≤s的总数。

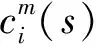
(6)

则序列AE可表示为：

AE(m,s,N)=φm(s)-φm+1(s),m≥2。

(7)

通过对序列的近似熵值进行计算，可以实现对序列复杂度的评估和分析。

2 基于五维超混沌的太赫兹调制跳变系统

2.1 太赫兹调制跳变系统结构

本文研究的调制跳变技术是数字通信系统中的调制解调部分，其系统模型如图1所示。主要包括调制方式分类、调制分类提取、调制方式排序3个方面。

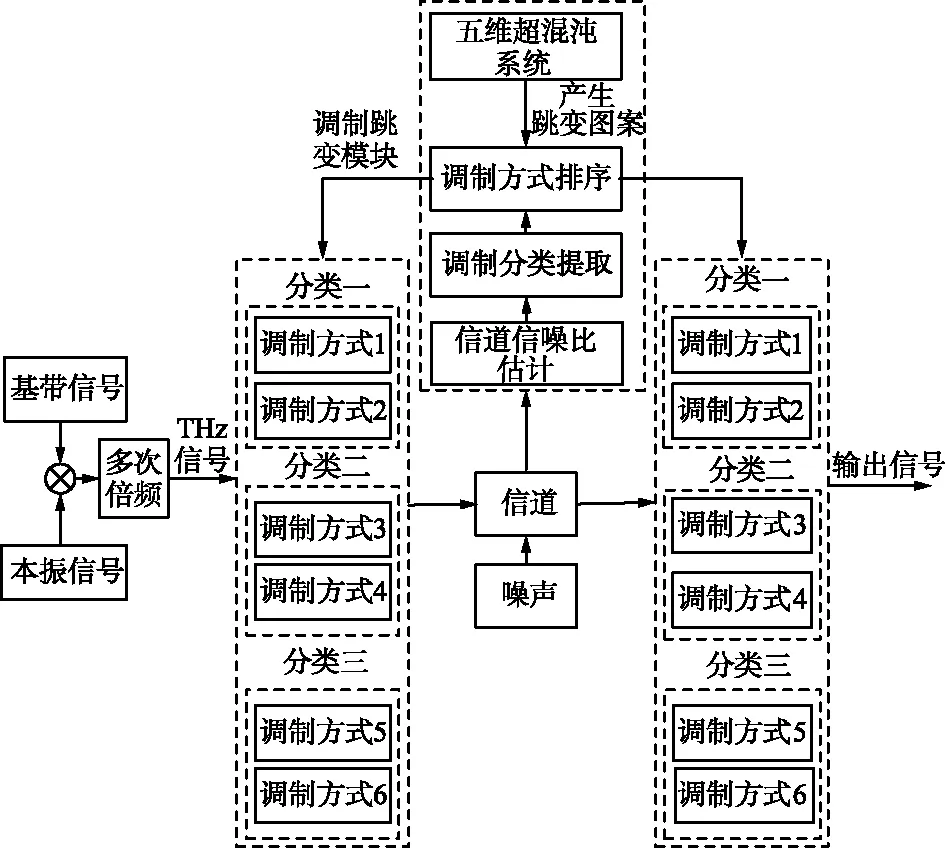
图1 调制跳变系统结构框图Fig.1 Structure diagram of modulation hopping system

根据图1所采用的太赫兹调制跳变系统。通过将基带信号和本振信号进行相乘混频滤波，产生混频信号，再经过多次倍频等环节获得所需频率的太赫兹信号。

在信号发射端设置多种调制方式，根据信噪比估计值提取并选择适合的调制类，再通过五维超混沌系统产生的跳变图案随机地选取一种调制方式。信号接收端需要根据先验的跳变图案进行解调，如果缺少先验信息则无法解调，使得太赫兹信号传输不易被截获，安全性更高。

2.2 跳变图案

构建好的五维超混沌系统可以产生具有强随机特性的实值序列，调制跳变需要在此基础上进一步将其转换成跳变图案，对式(2)产生的随机序列进行量化、映射处理。

本文采用扩大取模法对超混沌序列进行处理。首先去除实值序列整数部分，并将其小数部分扩大10n倍，进而根据量化级数进行取模运算，量化后序列q如下:

q=f1(f2(|xi-f2(xi)|×10n),K)，

(8)

式中，xi为超混沌实值序列，i=0,1,2,3,4；K为量化级数；n为扩大级数；f1(x,y)为取余函数；f2(x)为向下取整函数。

在每种调制类别中设置2种调制方式，所以K取值为2，即产生的序列q值只有0和1两种情况，跳变图案值为2。因此，本文采取一种简单的映射方法，设置门限值为10 000，当序列值低于门限值时映射为第一种调制方式，否则选择第二种调制方式。

2.3 调制分类提取

在无线通信中，信道的信噪比(Signal to Noise Ratio,SNR)是一个重要指标。在根据误码率和信噪比关系对调制方式进行分类之后，可以选择信噪比作为控制参数，以此来确定在不同时刻具体使用哪一种调制类别。

目前比较常用的信噪比估计是基于时域的算法，其中最经典的是最大似然估计法，其通过对序列进行训练或对反馈序列进行判决，以此来构造似然函数。但是，这种算法不适用于信号功率低、信噪比不理想的通信信道，会带来一定的误差。此外，由于太赫兹信号具有高频率、低功率等特殊性，太赫兹通信过程中受到的干扰主要来自高斯白噪声。针对上述情况，本文拟采用一种频域SNR估计算法。

图2为接收信号频域图。

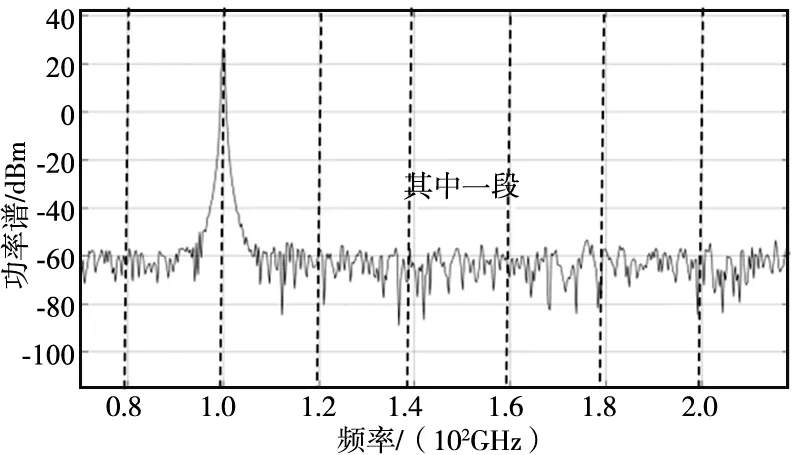
图2 接收信号频域图Fig.2 Frequency domain diagram of received signal

频域SNR估计算法步骤如下：

(1) 先对接收信号进行滤波处理；

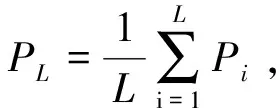
(3) 根据信号的频谱特性，在集合u中分别找出与Pm(m=1,2,…,L)左右距离最近且平均功率小于Q的两段值Pn,Pk(n,k=1,2,…,L,n≠k≠m)，对Pn与Pk的频率进行差值计算，可求出发射信号所在的频率范围，以及发射信号的平均功率PX，即:

(9)

(4) 将步骤(3)中所求得的频率范围剔除，剩下的部分就是噪声PN，对剩下的部分求均值，可得噪声的平均功率，即:

(10)

(5) 根据步骤(3)和步骤(4)计算出接收信号的SNR估计值。

3 仿真结果及分析

本文设置的仿真条件为:选择ASK,FSK,PSK,MSK,2DPSK,2QAM六种调制方式，并在每种调制类别中设置2种调制方式。基带为170 GHz太赫兹信号，信道为高斯白噪声。

3.1 SNR估计

在高斯白噪声下，传统的时域估计算法和频域估计算法的信噪比如图3所示。

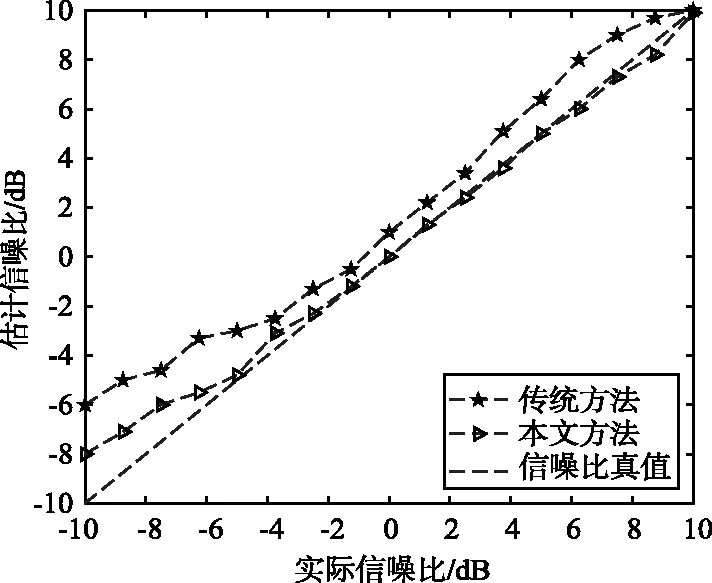
图3 不同估计算法的信噪比Fig.3 SNR of different estimation algorithms

相比于传统的时域估计算法，所提出的频域方法的信噪比估计值更贴近于真值。由于频域方法对信号中噪声剔除的比较干净，所以信噪比估计性能更好。

3.2 系统复杂度验证

混沌序列的AE越大，序列的复杂度越高，其混沌性也就越好。本文对传统的Logistic序列、三维混沌系统、文献[18]所设计的六维超混沌系统，以及本文所提的五维超混沌系统进行仿真对比，得到的仿真结果如图4所示。

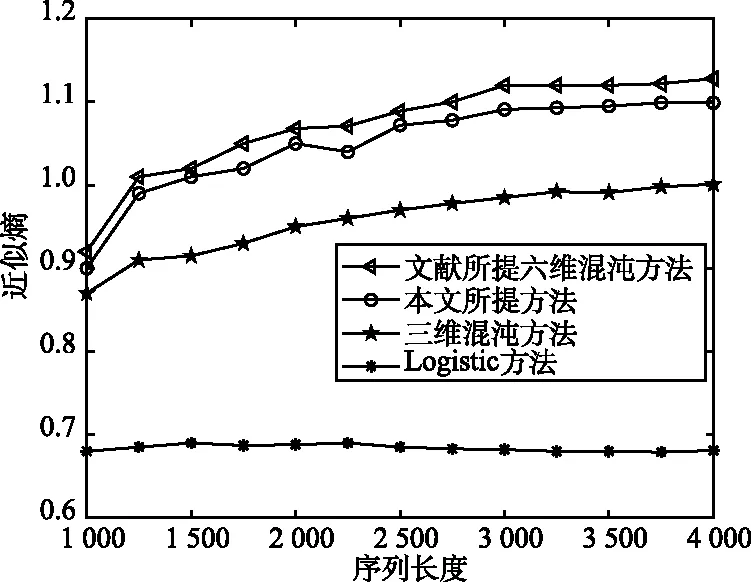
图4 不同混沌序列的近似熵值Fig.4 AE of different chaotic sequences

通过图4的仿真对比可以看出，在序列长度不断增加的情况下，Logistic序列的近似熵基本保持在0.68左右，而其他三种算法的近似熵随着序列长度的增加逐渐变大，即系统复杂度也在不断增加。并且可以看出，一维的Logistic序列的近似熵值明显低于其他序列，文献提出的六维超混沌系统的近似熵值最高，并最后稳定在1.12左右，其次是本文所提出的五维超混沌系统，最后稳定在1.1左右。

由仿真结果可以看出，本文所提的五维混沌系统的近似熵值接近六维混沌系统，差别不大，但明显优于三维混沌系统。同时，由于随着混沌系统维数的增加，系统计算复杂度呈明显增加趋势。因此，本文所提的五维混沌系统综合性能更好。

3.3 太赫兹调制信号

在误码率eBER=10-4情况下，可以计算出不同调制方式所需的信噪比，如表1所示。

表1 不同调制方式所需SNR

根据表1，将这6种调制方式为三类，即A={ASK，FSK}、B={PSK,MSK}、C={2DPSK,2QAM}。对太赫兹信号进行调制跳变和解调，信号源和接收机一直处于工作状态，所得到的仿真结果如图5所示，其中横坐标为信号频率，纵坐标为信号功率。

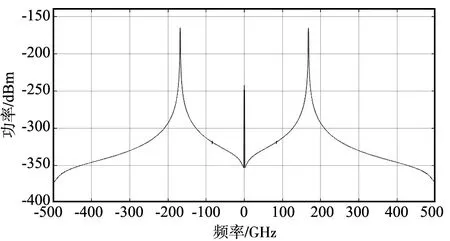
(a) 调制前的太赫兹信号

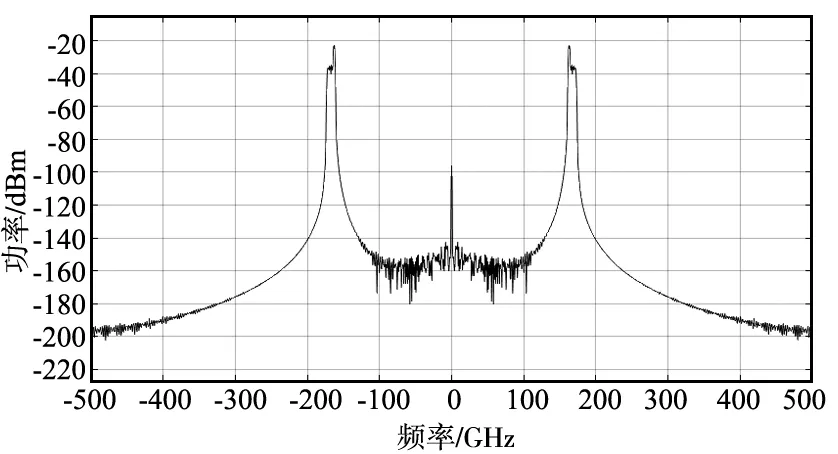
(b) 解调后的太赫兹信号图5 调制解调信号对比Fig.5 Comparison of modulation and demodulation signals

由仿真结果可知，当频率为170 GHz的太赫兹信号经过调制跳变系统后，输出的信号波形与输入信源信号波形几乎无明显变化。同时，结合信噪比估计和系统复杂度验证的仿真结果，说明本文所提方法有较好的抗截获性能。

4 结束语

本文在传统的三维Lorenz混沌系统基础上，提出一种基于五维超混沌系统的太赫兹调制跳变方法，通过信噪比估计、排列组合熵计算和调制信号仿真，定量地说明了该方法可以得到更精确的信噪比和更高的系统复杂度，使得调制信号具有更好的抗截获性能。综上所述，与传统的抗截获方法相比，所提的五维超混沌太赫兹跳变系统可以大大地增强系统的安全性和稳定性，因此适用于对太赫兹通信系统的二次加密。