一类一阶常微分系统周期边值问题正解的存在唯一性
2022-03-29何婷
何 婷
(西安电子科技大学数学与统计学院, 西安 710126)
1 引 言
本文研究如下一阶常微分系统

(1)
的周期边值问题的正解的的存在唯一性,其中a,b:[0,1]→[0,∞)连续且在[0,1]的任何子区间上不恒为0,f,g:R→R连续,f(0)≥0,g(0)≥0,且f(t),g(t)关于t∈[0,∞)是单调递增的.
近年来,一阶常微分方程(组)正解的存在性得到了广泛研究[1-9].其中,2001年Zhang 等[7]运用 Krasnoselskii 不动点定理,在一定条件下得到了问题
y′(t)=-a(t)y(t)+λh(t)f(y(t-τ(t)))
(2)
正周期解的存在性.其中a(t),h(t),τ(t)是连续的T-周期函数,a(t),h(t),f(t)非负, 存在t0∈[0,T]使得a(t0)>0.同时, 诸多学者致力于研究相应于问题(2)的微分系统[10-12],如2012年Chen等[11]讨论了问题
ui′(t)=-ai(t)ui(t)+
λbi(t)fi(u),i=1,2,...,n
(3)
正周期解的存在性,其中u=(u1,u2,...,un)∈Rn,得到如下结果:
定理A 设
(i)ai,bi∈C(R,[0,∞))是ω-周期函数且



则存在正数λ*,使得当0<λ<λ*问题时(3)至少存在两个正周期解;当λ=λ*时问题至少存在一个正周期解;当λ>λ*时问题不存在正周期解.
然而,就我们所知,多数文献都只是研究了问题的正周期解的存在性、多解性及不存在性,而少有得到正解的唯一性.一个自然的问题是:什么条件能保证一阶常微分系统(1)正解的存在性及唯一性?本文试图在f于0和∞处超线性(次线性),g于0和∞处次线性(超线性)条件下对研究问题(1)正解的存在性及唯一性进行探讨.
本文总假定:
(H1)a,b:[0,1]→[0,∞)连续且a,b在[0,1]的任何子区间上不恒为0;
(H2)f,g:R→R连续;
(H3)f(0)≥0,g(0)≥0,f(t),g(t)关于t∈[0,∞)单调递增.
本文的主要结果如下:
定理1.1设(H1)~(H3)成立且

则问题(1)至少有一个正解(u,v)∈(C1[0,1])2.
定理1.2设(H1)~(H3)成立且
(H6)f(t)在t∈(-∞,0]单调递减;

则问题(1)至少有一个正解(u,v)∈(C1[0,1])2.
定理1.3设(H1)~(H3)成立且
(H9) 存在p,q>0且pq<1使得对任意τ∈(0,1)有f(τt)≥τpf(t)及g(τt)≥τqg(t),t>0.则问题(1)至多有一个正解(u,v)∈(C1[0,1])2.
2 预备知识
引理2.1[13]设G1(x,y),G2(x,y)分别为边值问题

(4)
和

(5)
的格林函数.计算可得
寡日照天气对设施内辐射、温度和相对湿度均有影响,其中对辐射的影响要大于对温度和相对湿度的影响。本研究建立的寡日照条件下番茄生长模型可用于模拟分析不同程度寡日照条件对设施番茄生长的影响。相对于番茄叶面积指数和株高,寡日照天气对生物量的影响程度最为显著。
易见存在m,M>0,使得
0 引理2.2设(H1)~(H3)及(H6)~(H7)成立.则存在常数G>0,使得对于δ∈[0,1],问题 的所有解有 max{‖u‖∞,‖v‖∞}≤G, 证明 由引理2.1,问题(6)等价于如下积分方程组: (7) 设(u,v)是问题(6)的解.根据假设(H3),(H6)和Gi(x,y)>0,i=1,2得u,v≥0.由假设(H7),存在A>0,使得 (8) 如果‖u‖∞≤A, 则‖v‖∞≤Mf(A).同理,如果‖v‖∞≤A则‖u‖∞≤Mg(A).若‖u‖∞>A,‖v‖∞>A则有 ‖u‖∞≤Mg(‖v‖∞) (9) 和 ‖v‖∞≤Mf(‖u‖∞) (10) 结合(8)~(10)式可得 所以‖u‖∞>A,‖v‖∞>A不成立.综上,令 G=max{A,Mf(A),Mg(A)}. 引理得证. Z={u∈C[0,1]:α≤u(x)≤β,x∈[0,1]}. 显然Z为X的有界闭凸集. 定义算子T:Z→X, Tu(x)= x∈[0,1]. 对于任意u∈Z, Tu(x)= mg(mf(α))≥α. 另一方面,又有 Tu(x)= Mg(Mf(β))≤β. 因此,Tu∈Z.根据Arzèla-Ascoli定理,T:X→X为全连续算子.由Schauder 不动点定理,至少存在一个u∈X满足Tu=u.再令 v(x)∈C1[0,1]满足 从而u(x)∈C1[0,1]满足 定理得证. 定理1.2的证明 设Y=(C[0,1])2,其范数定义为‖(u,v)‖=max{‖u‖∞,‖v‖∞}.则问题(7)的解等价于积分方程 的解(u,v)∈Y. 定义映射Lδ:Y→Y, 显然,任意δ∈[0,1],Lδ是紧算子.从而求解问题(1)等价于找映射L1在Y中的一个不动点. 设BG是Y上的一个球域, BG={(u,v)∈Y:‖(u,v)‖ 根据引理2.2可知,Lδ在边界∂BG上没有不动点.令I:Y→Y为单位映射.根据Leray-Schauder度的紧同伦不变性,任意δ∈[0,1],有 deg(I-L1,BG,0)=deg(I-Lδ,BG,0)= deg(I-L0,BG,0)=deg(I,BG,0)=1. 则L1在BG内有一个不动点(u,v).结合Gi(x,y)>0(i=1,2)和假设(H2),(H3),(H6),(H8),有u(x),v(x)>0,∀x∈[0,1].证毕. 定理1.3的证明 设(uj,vj),j=1,2是问题(1)的两个正解.定义 Λ={λ∈(0,1]:u1-θu2,v1-θv2≥0, x∈[0,1],θ∈[0,λ]} (11) 显然,Λ≠∅.令τ=supΛ并假设τ<1.则对于x∈[0,1]有 u1(x)-τu2(x)≥0,v1(x)-τv2(x)≥0. 由式(3)和假设(H2), (H9), 对于任意x∈[0,1]有 同理有v1(x)≥τpv2(x),x∈[0,1].进而有 -(u1(x)-τu2(x))′+a(x)(u1(x)-τu2(x))= g(v1(x))-τg(v2(x))≥(τpq-τ)g(v2(x)) 和 -(v1(x)-τv2(x))′+b(x)(v1(x)-τv2(x))= f(u1(x))-τf(u2(x))≥ (τpq-τ)f(u2(x)). 若对任意x∈(0,1)有f(u2(x))≡0,g(v2(x))≡0,那么这与u2(x),v2(x)是问题(1)的正解矛盾.从而一定存在x1,x2∈(0,1)满足f(u2(x1))>0,g(v2(x2))>0.又因为τpq-τ>0可以推出任意x∈(0,1), u1(x)-τu2(x)≥0,v1(x)-τv2(x)≥0, 则存在μ>λ使得μ∈Λ.这与τ=supΛ矛盾.因此,τ=1,且对于任意x∈[0,1], u1(x)-u2(x)≥0,v1(x)-v2(x)≥0. 同理,对于任意x∈[0,1],有 u1(x)-u2(x)≤0,v1(x)-v2(x)≤0. 从而u1=u2,v1=v2.定理得证. 当问题(1)变为 时,同样也可以得到问题正解的存在性及唯一性,即下面的条件结果. 假设 (H1′)a,b:[0,1]→[0,∞)连续且a,b在[0,1]的任何子区间上不恒为0; (H2′)f,g:[0,1]×R→R连续; (H3 ′) 对于任意x∈[0,1],f(x,0),g(x,0)≥0,且f(x,t),g(x,t)关于t∈[0,∞)单调递增. 定义 及 定理4.1设(H1′)~(H3′)成立且 则问题(12)至少有一个正解(u,v)∈(C1[0,1])2. 定理4.2设(H1′)~(H3′)成立且 (H6′) 对于任意的x∈[0,1],f(x,t)在t∈(-∞,0]单调递减的; (H8′) 存在x,y∈[0,1],f(x,0)>0且g(y,t)>0,t>0. 则问题(12)至少有一个正解(u,v)∈(C1[0,1])2. 定理4.3设(H1′)~(H3′)成立且 (H9′) 存在p,q>0且pq<1使得对任意τ∈(0,1)有f(x,τt)≥τpf(x,t)及 g(x,τt)≥τqg(x,t),t>0,x∈[0,1]. 则问题(12)至多有一个正解(u,v)∈(C1[0,1])2. 定理4.1的证明 定义算子T′:Z→X, T′u(x)= x∈[0,1]. 对于任意u∈Z,有 mk(mh(α))≥α. 另一方面,有 MG(MF(β))≤β. 后面的证明与定理1.1的证明过程一样,略.证毕. 定理4.2和定理4.3的证明分别与定理1.2和定理1.3的证明过程类似. 考虑方程组 其中0 容易验证假设(H1)~(H3)成立.此外,∀c>0,有 从而假设(H4)成立,同理,假设(H5)成立.另外,当τ∈(0,1)时,有 同理,当τ∈(0,1)时有g(τv)>τpg(v).假设(H9)成立.因此,结合定理1.1和定理1.3,问题存在唯一正解(u,v)∈(C1[0,1])2.
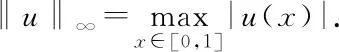


3 主要结果的证明
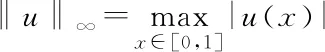

















4 主要定理的推广




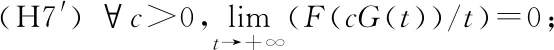









5 应 用
