生物统计附试验设计教学中引入效力分析的思考

吴江鸿

（内蒙古民族大学动物科技学院，内蒙古 通辽 028000）

x2检验与u检验是生物统计学中最常用的两种假设检验，两者均可检验服从二项式分布的样本。在遗传学研究中，常常会对两种质量性状利用统计次数法获取次数资料，如教学中常用x2检验分析两种毛色动物的杂交F2代出现的毛色分离比例是否符合某种遗传比例[1]。同时这类问题也可转化成某一种性状属性的观测百分数是否与理论百分数相同的形式，这样就可以利用单个样本百分数的假设检验进行分析。

本文就明道绪、刘永健主编的第六版生物统计附试验设计中127页的例7.1进行比较分析[2]，发现两种方法得出的结论不同。进而引入效力分析比较了两种检测方法的可靠性。

1 利用x2的假设检验

【例】观察白色羊与黑色羊杂交F2代的毛色，其中白色羊为181只，黑色羊为79只。检验白色羊与黑色羊杂交在F2代的毛色分离是否符合3∶1的理论比例。

本题属性类别数k=2，df=k-1=2-1=1，所以进行x2检验须对x2作连续性校正，计算x2c。检验步骤为:

提出无效假设与备择假设。

H0:白色羊与黑色羊杂交在F2代的毛色分离符合3:1的理论比例；

HA:白色羊与黑色羊杂交在F2代的毛色分离不符合3∶1的理论比例。

计算理论次数。

假定白色羊与黑色羊杂交在F2代的毛色分离符合3∶1的理论比例，计算理论次数：

白色的理论次数T白=260×3/4=195

黑色的理论次数T黑=260×1/4=65

x2c的计算。

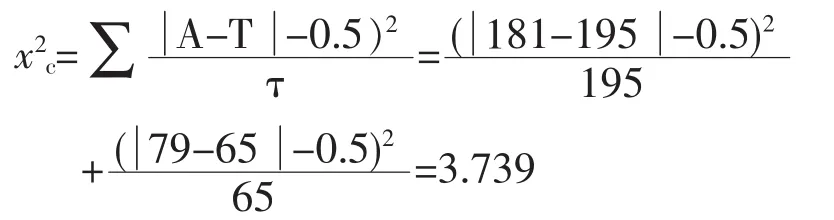
统计推断。

查 x2表得 x20.05(1)=3.84，x2c=3.739＜x20.05(1)，P＞0.05，接受无效假设H0白色羊与黑色羊杂交在F2代的毛色分离符合3∶1的理论比例。

2 利用u的假设检验

该例可根据F2代羊群中不同毛色羊在整体中所占比例与其理论比例进行比较（见图1），即根据某一特定毛色羊分类为单个样本的百分数的假设检验。

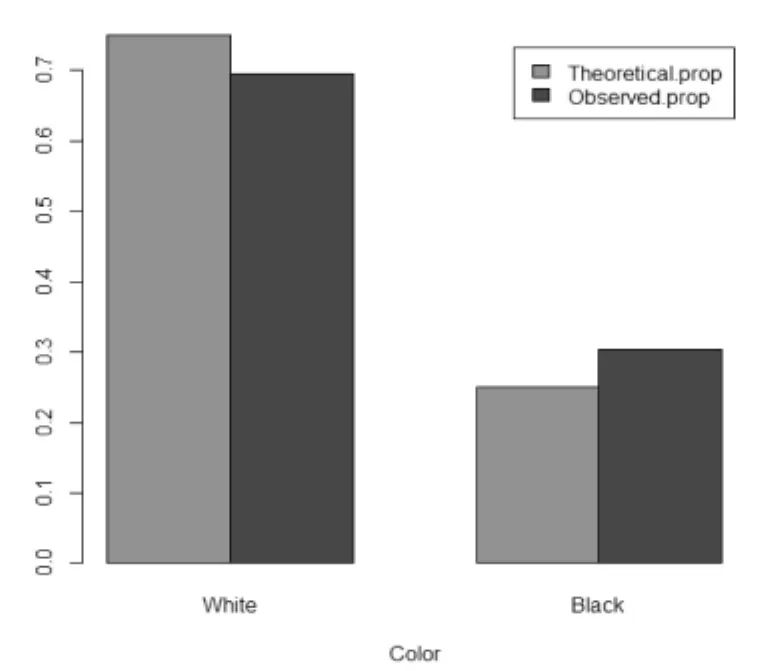
图1 F2代羊群中黑白毛色观察比例与理论比例

2.1 比较白色羊的比例与理论遗传比例

如将该题进行变形，计算260只F2代羊群中白色羊的观察比例样本百分数白是否与其理论遗传比例p0相一致，则为单个样本百分数的假设检验。

H0:p=75%，该群体中白色羊的比例与理论遗传比例相同；

HA:p≠75%，该群体中白色羊的比例与理论遗传比例不相同。

u值计算。

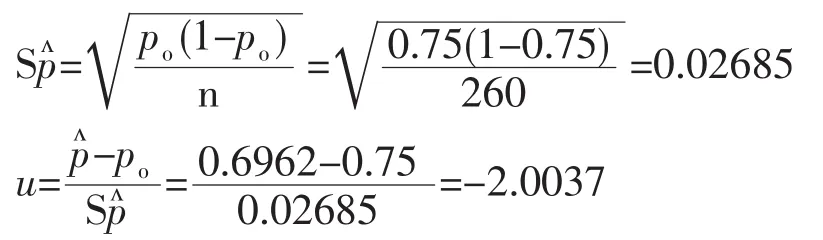
统计推断。

|u|＞1.96，所以 P＜0.05，因此否定 H0，接受 HA:p≠75%，该群体中白色羊的比例与理论遗传比例不相同。

2.2 比较黑色羊的比例与理论遗传比例

如将该题进行变形，计算260只F2代羊群中黑色羊的观察比例样本百分数黑是否与其理论比例p0相一致，此时，，np0=260×25%=65＞30，不用对 u 进行连续性校正。检验步骤为：

提出无效假设与备择假设。

H0:p=25%，该群体中黑色羊的比例与理论遗传比例相同；

HA:p≠25%，该群体中黑色羊的比例与理论遗传比例不相同。

u值计算。

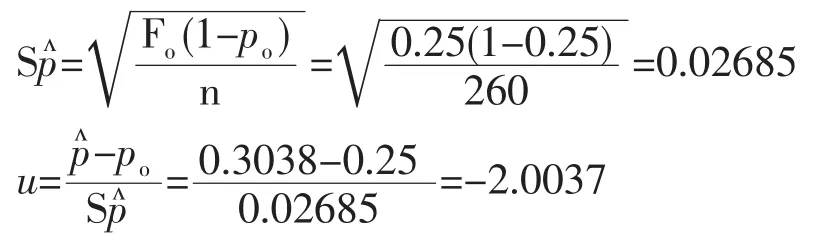
统计推断。

u＞1.96，所以 P＜0.05，因此否定 H0，接受 HA:p≠25%，该群体中黑色羊的比例与理论遗传比例不相同。

3 两种检验方法的效力分析

为了比较两种方法对同样的样本数据进行检验时出现不同的结果，本节将系统地比较x2检验与u检验的应用场景与效力等问题。通过比较x2检验与u检验对同一样本数据的假设检验发现，在0.05显著水平下，两种方法得出的结论相反。即表明如果该样本中白色羊与黑色羊杂交在F2代的毛色分离符合3∶1的理论比例是真实存在的，那么x2检验的结果正确。这样就说明u检验在对该样本数据的检验过程中犯了一类错误。

如果该样本中白色羊与黑色羊杂交在F2代的毛色分离符合3∶1的理论比例，x2检验的结果不正确，这就说明x2检验在对该样本数据的检验过程中犯了二类错误。为了比较两种检验方法的可靠性，首先列出两种检验方法的应用场景与条件（见表1）。

表1 u检验和x2检验的比较

x2检验与u检验在该试验样本的分析中哪种更可靠一些,对此需要进行可靠性检测。效力分析（Power Analysis）对于试验设计非常重要，它可帮助确定在指定显著性水平下开展某项试验所需要的样本量，并通过评估该试验设计的统计效力，给出在现有的样本量下该试验结论的可靠性[3]。如果结论的可靠性非常低，那么完全可以宣布这个试验是无效的，应该修改或者终止试验[4]。本文利用R软件包pwr对两种检验方法进行了效力分析[5]。将两者的显著水平都设置为0.05，样本数设定为260。计算该样本数据在两种检验方法下的效应值：x2检验的效应值为effect.size=ES.w1(P0,P1)=0.1242458；而以黑色羊为例检验的效应值为=0.0538。然后分别计算两者的检测效力 （power），power （x2）=0.5173613，而 power（u）=0.1396603。从结果可知，两种方法在样本量为260的情况下效力值都不是很理想，没能达到 0.8。但是 power（x2）＞ power（u），比较而言x2的检测效力更高一些，较为可靠。

4 结论

在本科教学中引入检测效力的概念非常重要，每一种假设检验方法在处理不同样本数据时的检测效力是不同的，不能将统计学的公式简单带入，求出P值就万事大吉，要分析不同假设检验的检测效力，以及判断得出的结论是否可靠。另外效力分析（Power Analysis）对于试验设计也非常重要，它可以帮助确定在指定显著性水平下开展某项试验所需要的样本量，更可以帮助研究者进行更合理的试验设计。