阻力和升力加速度指令快速解析与跟踪制导
2022-03-29刘刚
刘刚
(中国运载火箭技术研究院,北京 100076)
升力式飞行器在大气层内的滑翔段一般有初始能量过剩、准平衡滑翔、倾侧转弯和无动力等特点,其制导任务通常是使飞行器在到达给定的待飞纵程时将其高度、速度、航迹方向角、弹道倾角等多个参数控制到期望的值,以实现和下一个飞行段的顺利衔接。解决滑翔段制导问题应用较多的制导方法有预测校正制导[1-9]、阻力加速度跟踪制 导[10-14]、三 维 制 导[15-16]、解 析 制 导[17-21]等。在预测校正制导中,攻角剖面一般事先给定为一个随速度或马赫数变化的固定剖面,在制导中攻角仅在给定剖面基础上做小幅调整。攻角是一个重要的控制量,预测校正制导中给定攻角剖面的做法在一定程度上制约了攻角在制导中的作用。阻力加速度跟踪制导是一种成功获得航天飞机的工程应用的制导方法,但是该方法依赖于参考轨迹,灵活性不强。相比于其他方法,解析制导的研究相对较少。文献[17]把准平衡滑翔条件与解析预测制导相结合,形成一种不依赖参考轨迹和攻角剖面的滑翔段解析制导方法,该方法用倾侧角进行航向和终端速度控制,用攻角进行终端高度和纵程控制,取得了较好的效果,说明解析法用于滑翔段制导具有可行性。文献[19]以谱分析法寻求运动方程的解析解,并形成再入解析制导方法,但是其数学工具比较复杂,应用难度较大。
本文尝试探索一种基于直接解析的滑翔段制导方法。思路如下:首先,利用阻力加速度和攻角的单调性关系,在每个制导周期实时设计出满足终端速度约束的阻力加速度指令,靠改变攻角进行跟踪,实现对终端速度的控制;其次,通过引入虚拟目标和伪视线角的概念,将比例导引应用于滑翔段,通过纵向比例导引生成航迹坐标系的升力加速度指令,靠改变倾侧角进行跟踪,实现对终端高度和终端弹道倾角的控制。对于航迹方向角(或待飞横程)的控制,通过倾侧角按反转走廊边界改变正负号实现。本文提供的方法可摆脱对参考轨迹和攻角剖面的依赖,计算量很小,可快速生成制导指令,实现对终端高度和终端速度的较高精度控制。
1 滑翔段制导问题
滑翔段制导问题可表述如下:假设飞行器已经处于准平衡滑翔飞行状态,当前待飞纵程为L0、高度为h0、速度为v0。制导终端约束为:使飞行器在待飞纵程为Lf时,高度为hf、速度为vf、弹道倾角为θf,航迹方向角偏差Δχf(或待飞横程)小于给定值。
2 终端速度的控制方法
注意到,在升力式飞行器滑翔段飞行的任一时刻,若其他参数都不变,只改变攻角大小,根据空气动力学原理,在约0°~90°的攻角范围内,飞行器阻力加速度的绝对值和攻角具有单调递增关系,攻角越大,阻力加速度的绝对值越大。利用这一特点,可以通过改变攻角获得期望的阻力加速度。只要设计出满足终端速度约束的阻力加速度指令,再通过改变攻角对其进行跟踪,就能实现对终端速度的控制。
2.1 阻力加速度指令在线快速解析
首先,需要设计满足终端速度约束的阻力加速度指令。假设飞行器自当前状态到终端状态的飞行时间为t,期间假设可以通过制导跟踪策略使得飞行器以固定的阻力加速度¯ax飞行,到达终端纵程时的速度为vf。忽略航迹方位角的影响,仅考察飞行器在纵向平面的运动,飞行路程s为

由牛顿一维质点运动学,有

由式(2)得

将式(4)代入式(3)可得



由式(5)和式(6)可得

为了适应不同飞行任务的要求,可再引入一个加权系数kax:

由式(1)、式(7)和式(8)有

阻力加速度指令加权系数kax可根据飞行任务的特点进行设计,加权系数剖面可以采用待飞纵程为横坐标进行设计,如图1所示。
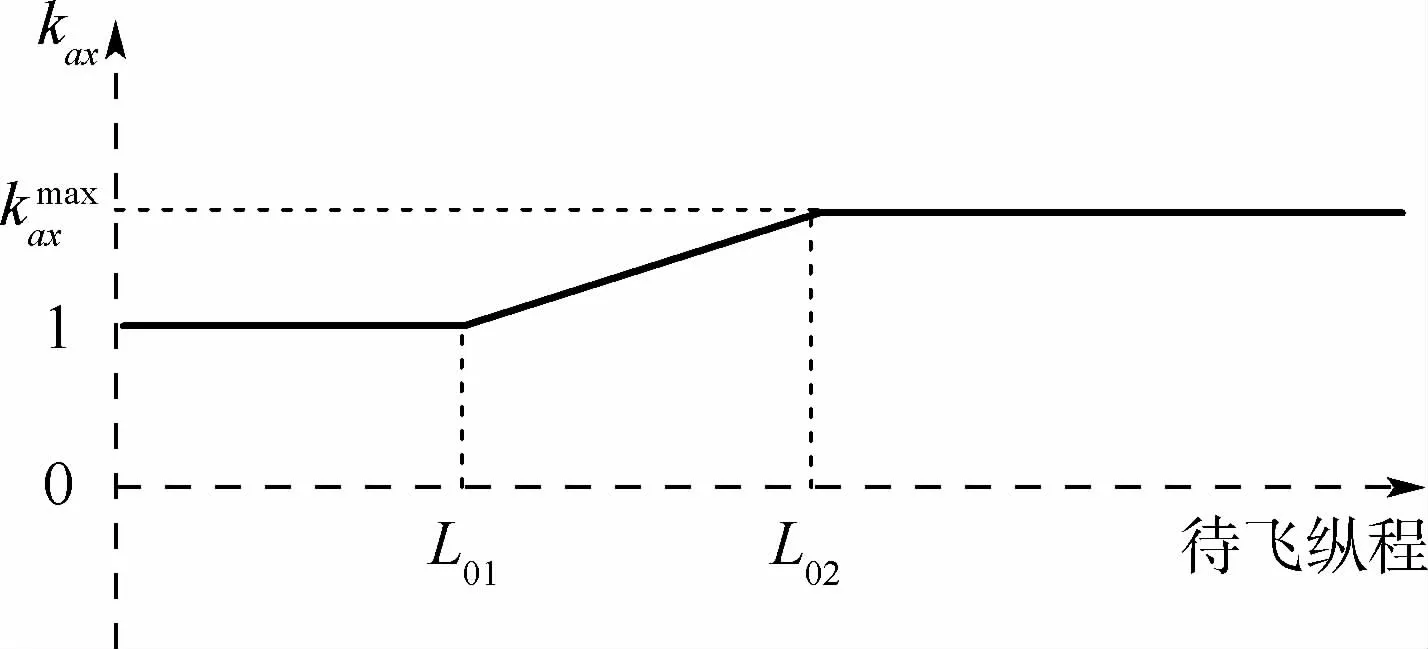
图1 典型的阻力加速度加权系数剖面Fig.1 Typical drag acceleration weighting coefficient profile
2.2 用攻角跟踪阻力加速度指令

式中:fx、fy为飞行器本体坐标系视加速度,对于无动力升力式飞行器仅由气动力产生,可由加速度计直接测量;αgx为惯性攻角,是在忽略风速的情况下由飞行器的地速和姿态角的导航值计算出的攻角估计值。
对于升力式飞行器,在一定攻角范围内,飞行器的阻力加速度和攻角具有单调性,攻角越大,阻力加速度的绝对值越大。因此,可以通过改变攻角对阻力加速度指令进行跟踪。
指令攻角α*(惯性值)以增量形式按下式计算:

式中:αgx为当前惯性攻角;kα为增益系数(正值)。
另外,需要根据飞行器姿态控制能力对指令攻角进行限幅和限速。由于本文方法中的攻角指令是增量形式的,kα取值与制导周期有关。若kα取值过大,将触发指令攻角限速,此时一般不会对制导精度产生不良影响,也不会出现攻角指令震荡;但是若kα取值过小,将影响阻力加速度跟踪效果。
2.3 倾侧角的阻力加速度跟踪模式


式中:σ*为在倾侧角的阻力加速度跟踪模式中指令倾侧角的大小;σmax1为在倾侧角在阻力加速度跟踪模式中的最大允许值,该值对于飞行初期的最大热流有很大影响,一般设计为小于全程倾侧角最大允许值σmax。σmax1过小会影响阻力加速度指令的跟踪效果,因此需要根据具体任务折中考虑。
进入倾侧角的阻力加速度跟踪模式的判据可按式(14)计算:
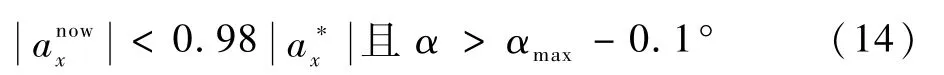
退出倾侧角的阻力加速度跟踪模式的判据可按式(15)计算:

为了简化制导逻辑,可在滑翔段初期直接将倾侧角置为阻力加速度跟踪模式。在后续飞行中,只要满足式(15)的判据,即退出阻力加速度跟踪模式,切换为升力加速度跟踪模式。后续不再重复进行模式切换。在升力加速度跟踪模式中,倾侧角将用于跟踪升力加速度指令,不再用于跟踪阻力加速度指令。
3 终端高度和终端弹道倾角的控制方法
比例导引是一种精度高、所需过载小的末制导方法。比例导引的原理是:先计算从飞行器到目标点的视线角和视线角速度,再使飞行器速度矢量的变化率与视线角速度成比例,这样即可使飞行器精确击中目标。但是,这种方式不能直接用于滑翔段制导,其原因是:滑翔段飞行距离很长,一般为数千公里,与地球半径达到同一数量级,受到地球曲率的影响,从飞行器到目标的视线会处于地平线以下,如果直接使用比例导引会使飞行器在飞行半途中坠地。这是将比例导引用于滑翔段制导需要解决的一个问题。为了在滑翔段应用比例导引,本文提出虚拟目标、伪视线角和伪视线角速度的概念,通过带倾角约束的纵向比例导引生成航迹坐标系的升力加速度指令,通过改变倾侧角进行跟踪,实现对终端高度和弹道倾角的控制。
3.1 基于比例导引的升力加速度指令解析方法
虚拟目标是指以制导终端纵程Lf和终端高度hf为特征参数的一个虚拟的目标。伪视线角是指在忽略地球曲率情况下计算的从飞行器到虚拟目标的视线角,伪视线角速度是指在忽略地球曲率情况下计算的从飞行器到虚拟目标的视线角速度。由于本文中比例导引仅用于纵向,不需要横向参数。在纵向,带终端弹道倾角约束的比例导引公式为
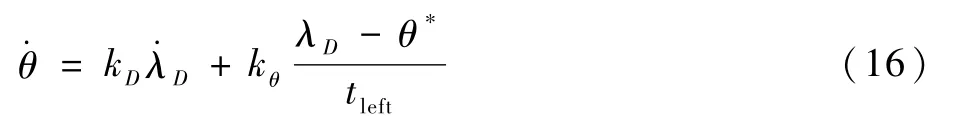
根据比例导引的原理,若满足式(16),可使飞行器以弹道倾角θ*击中虚拟目标。由虚拟目标的定义,可知这实际上正好满足了制导终端纵程、终端高度和弹道倾角约束。
式(16)中,纵向伪视线角速度和纵向伪视线角计算公式如下:
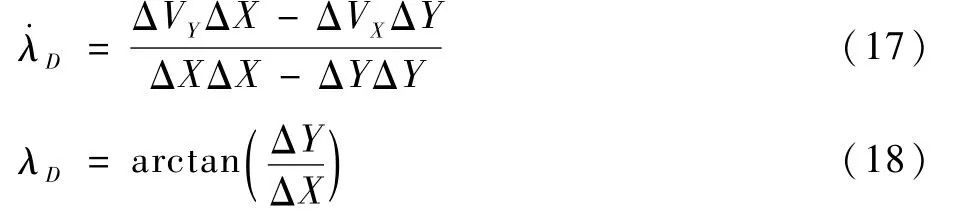
式中:ΔX、ΔY和ΔVX、ΔVY分别为从飞行器到虚拟目标的相对位置和相对速度,表达式为

剩余飞行时间tleft按下式估算:

由飞行动力学有
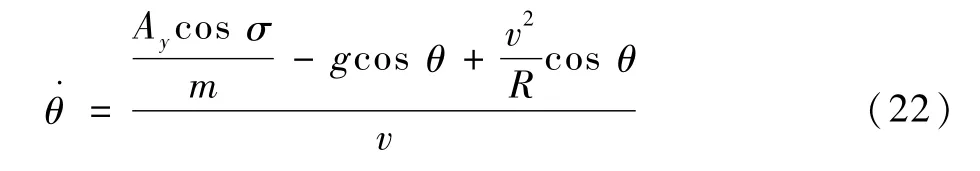
式中:Ay为飞行器的升力;R为飞行器到地心的距离;σ为飞行器倾侧角;m为飞行器质量;v为飞行器对地速度。
另外,定义:

由式(16)、式(22)和式(23)可得

式(24)即为基于比例导引的升力加速度指令(航迹坐标系)解析值,其中第1项为高度控制项,第2项为重力补偿项,第3项为离心力补偿项,第4项为终端弹道倾角控制项。这里,比例导引的相关参数都是由常规导航参数解析得到的,并不需要增加额外的传感器。
3.2 倾侧角的升力加速度跟踪模式

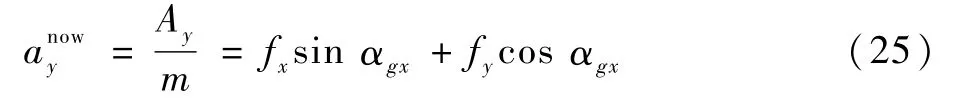


否则,

式中:σmax为最大允许倾侧角。
同样,需要根据飞行器姿态控制能力对指令倾侧角进行限速。本节的控制策略仅得到倾侧角的大小,倾侧角的正负由第4节策略确定。
4 航迹方向角控制方法
第2节和第3节中的方法给出了攻角指令(含正负号)和倾侧角指令(仅绝对值),用于进行速度、高度和弹道倾角控制。在3.2节中,飞行器多余的升力加速度被倾侧角分配到侧向,会影响飞行器的侧向运动。为了对航迹方向角偏差Δχ(或待飞横程H)进行控制,采用与预测校正制导类似的方法,设计一个侧向偏差走廊,当飞行器侧向运动超出走廊边界时,通过改变倾侧角的符号进行横向控制。典型的侧向偏差走廊如图2所示。
航迹方向角偏差Δχ定义为

式中:χt为飞行器当前的航迹方向角;At为从当前飞行器到目标的大地方位角。χt和At都以指向当地正北为零,以向东偏为正。
指令倾侧角的符号Signσ初始值为
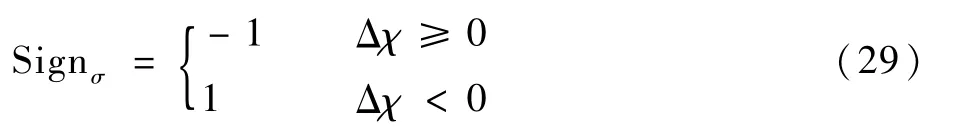
后续倾侧角反转触发逻辑为:若当前Signσ=-1且Δχ≤-Δχmax时,触发正向反转;若当前Signσ=1且Δχ≥Δχmax时,触发负向反转。Δχmax为按图2计算的侧向偏差走廊边界。
5 过程约束的满足途径和方法流程
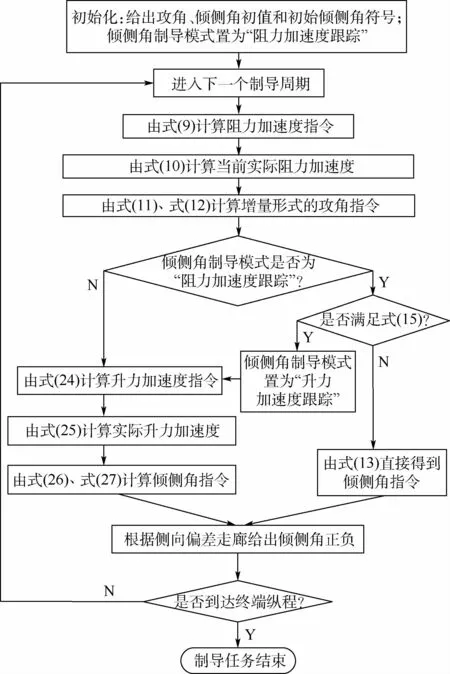
图3 制导方法流程Fig.3 Flowchart of guidance method
6 仿真校验
6.1 模型参数
采用文献[10,22]中的飞行器参数,飞行器质量为1 000 kg,参考面积为3.5 m2,升力系数和阻力系数按下式计算:
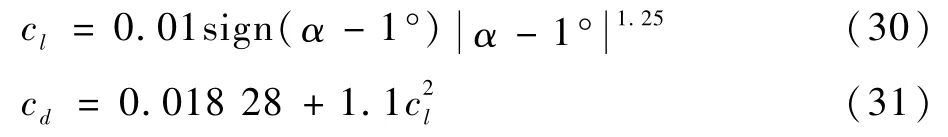

表1为任务初始和终端参数。表中:λ为经度,φ为大地纬度。终端条件为距离目标点(经度27.85°,纬度0°)的待飞纵程为100 km。对于终端坐标无具体要求。仅有终端速度、高度、航迹方向角偏差和弹道倾角要求。文献[10]中无弹道倾角约束,本文为了验证方法额外附加了终端弹道倾角约束。过程约束为过载小于5g,驻点热流小于2 500 kW/m2,动压小于15 000 Pa。

表1 任务初始和终端参数Table 1 Initial and terminal parameters of task
6.2 约束条件敏感因素分析
1)最大热流的敏感因素分析
考察倾侧角在阻力加速度跟踪模式中的最大允许值σmax1对最大热流的影响。分别将σmax1取为70°、80°、90°,其余仿真条件都相同,仿真结果如图4所示。可见,σmax1越大,最大驻点热流越大。因此,需要合理选取σmax1。

图4 σmax1取不同值时的最大驻点热流Fig.4 Maximum stagnation heat flux for different values ofσmax1
2)最大动压的敏感因素分析
首先,考察阻力加速度加权系数剖面对动压的影响。在图1所示的剖面中,分别取如表2所示参数设置。
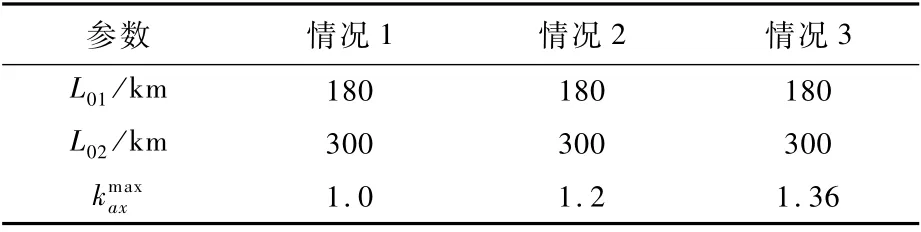
表2 阻力加速度加权系数剖面设计Table 2 Design of drag acceleration weighting coefficient profile

图5 阻力加速度加权系数最大值取不同值时的动压Fig.5 Dynamic pressure for different drag acceleration weighting coefficient maximum values
其次,考察期望终端弹道倾角对动压的影响。将期望终端弹道倾角θ*分别取0°、-2°、-4°,其余仿真条件都相同,仿真结果如图6所示。可见,当将期望终端弹道倾角θ*取0°时,最大动压达到17 000 Pa以上,超出了约束值,当θ*取-2°或-4°时,最大动压大幅减小。产生这种现象的原因是:为了拉平终端弹道倾角,会使飞行器在速度较高时高度降低,处于大气密度较大的环境。
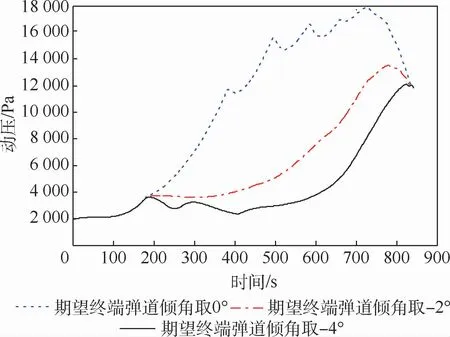
图6 期望终端弹道倾角取不同值时的动压Fig.6 Dynamic pressure for different expected terminal trajectory inclination angles
6.3 标称状态下仿真
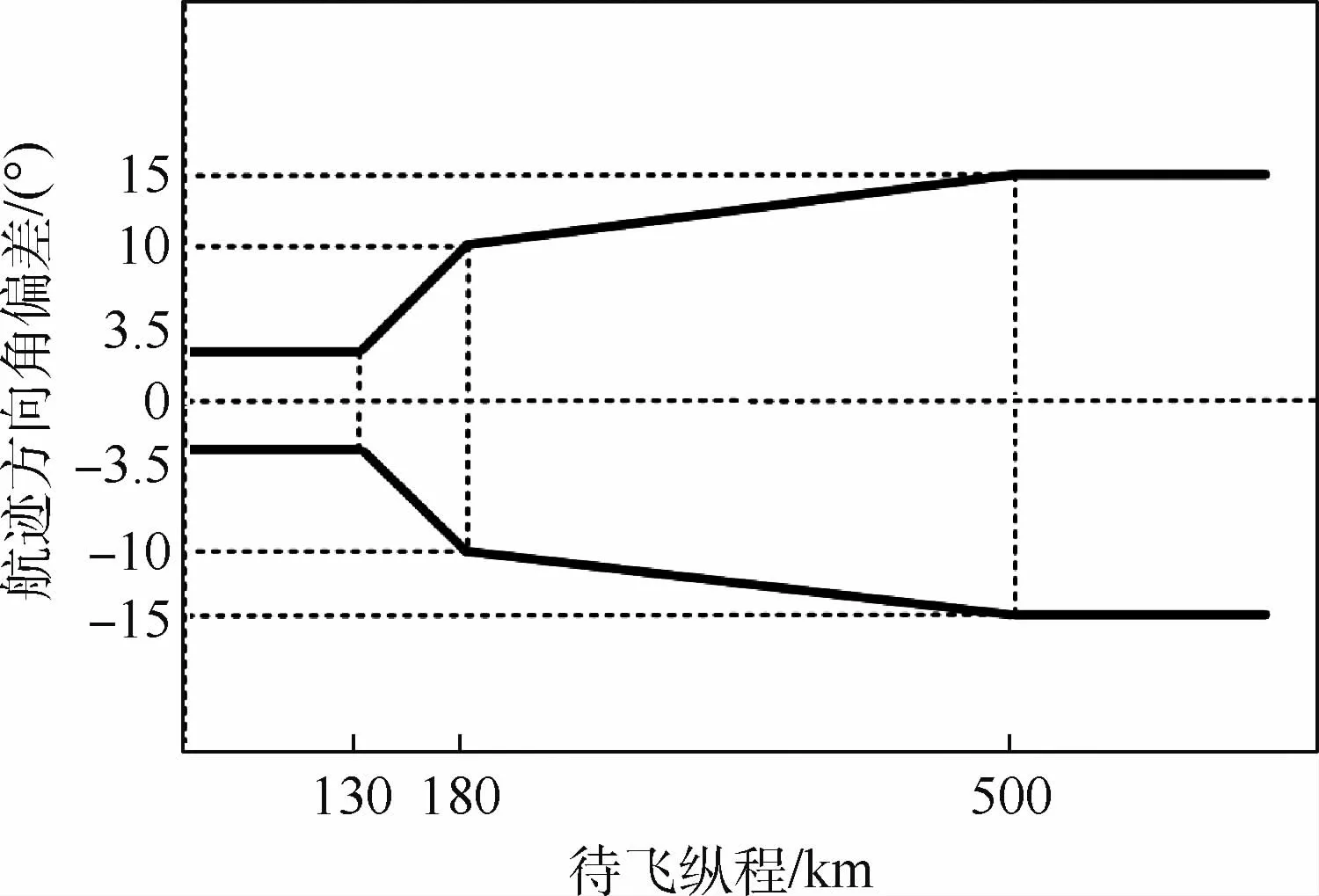
图7 侧向偏差走廊设计Fig.7 Design of azimuth deviation corridor
在标称状态下进行仿真,在距离目标点(经度27.85°,纬度0°)的待飞纵程小于或等于100 km时仿真结束。仿真曲线如图8~图18所示。
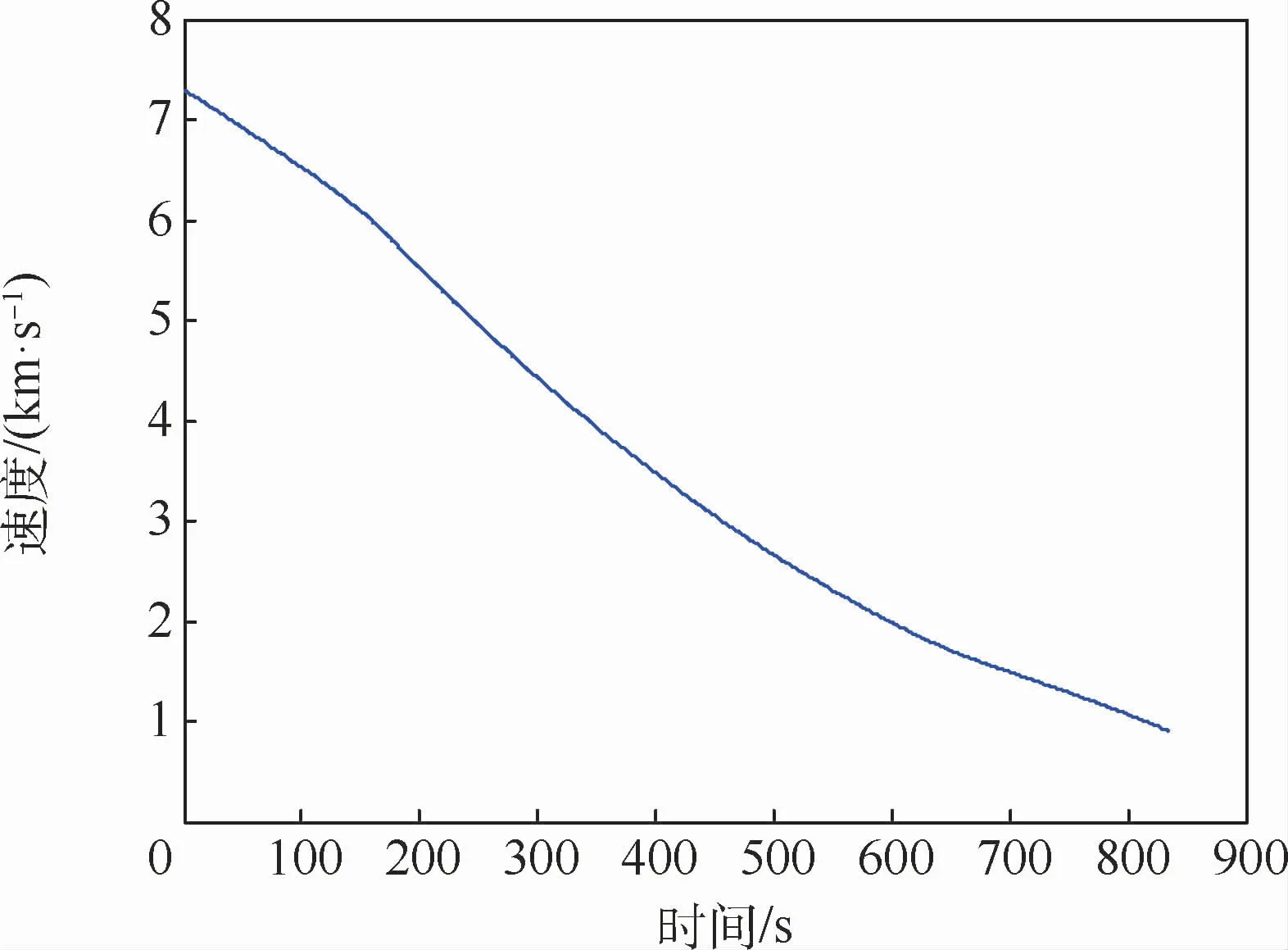
图8 速度曲线Fig.8 Velocity curve
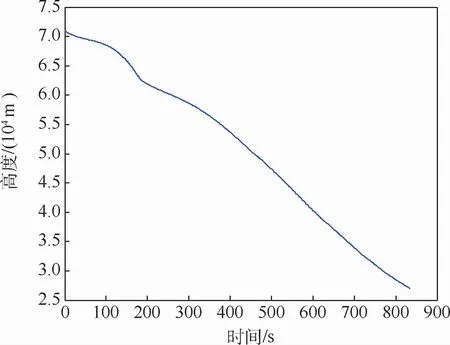
图9 高度曲线Fig.9 Height curve

图10 弹道倾角曲线Fig.10 Trajectory inclination angle curve
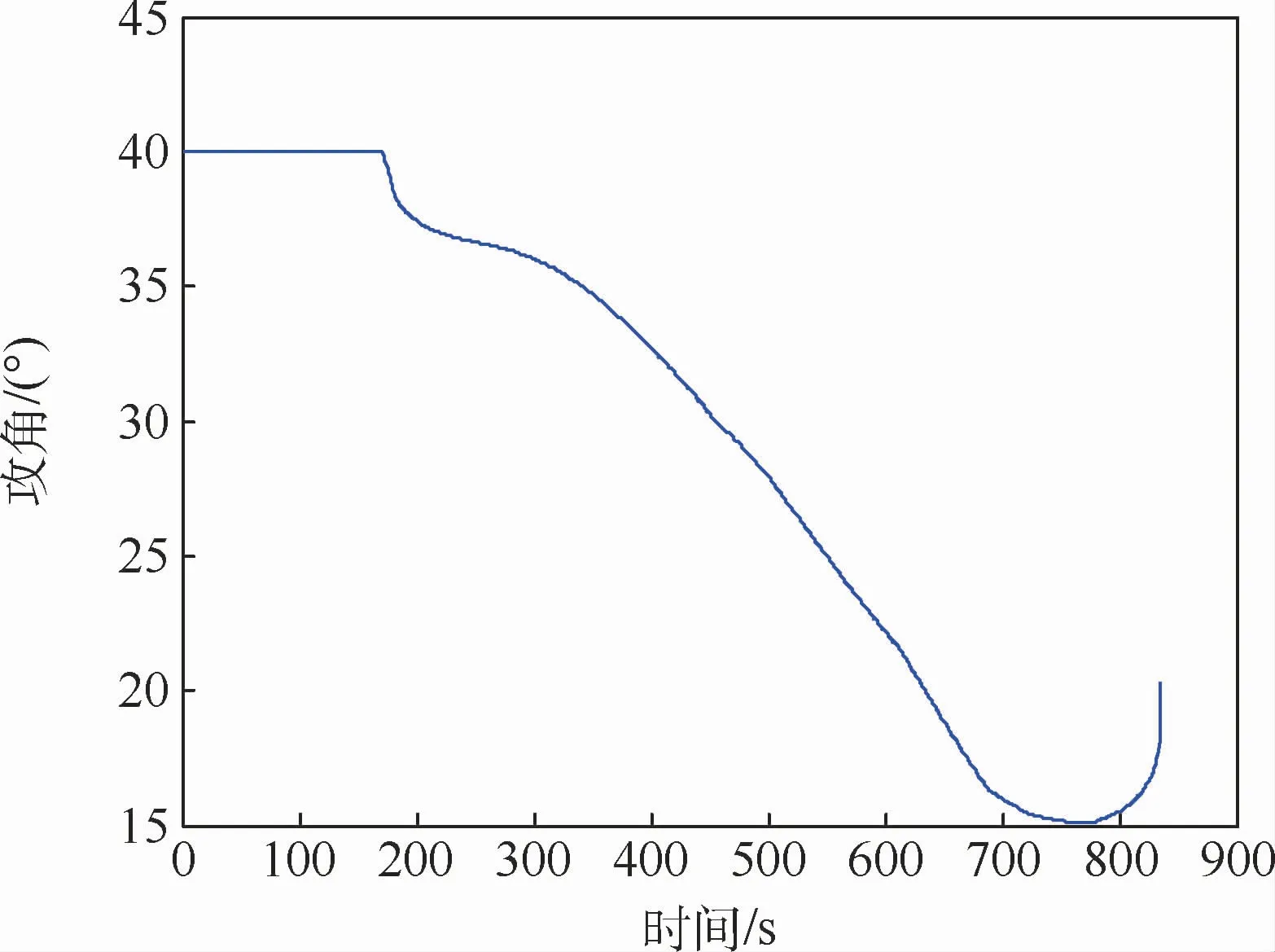
图11 攻角曲线Fig.11 Attack angle curve

图12 倾侧角曲线Fig.12 Inclination angle curve
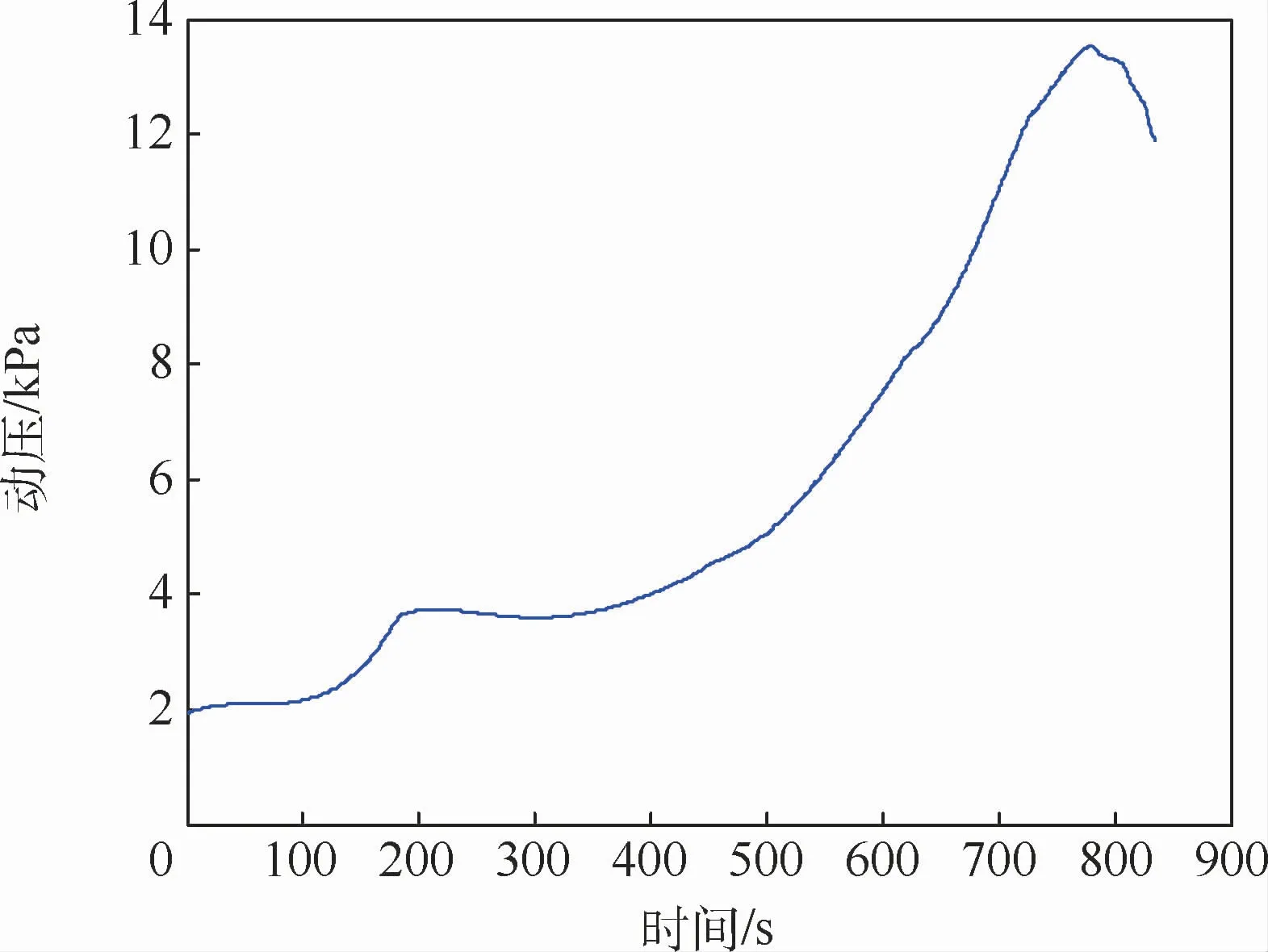
图13 动压曲线Fig.13 Dynamic pressure curve

图14 驻点热流曲线Fig.14 Stagnation heat flux curve

图15 法向过载曲线Fig.15 Normal overload curve
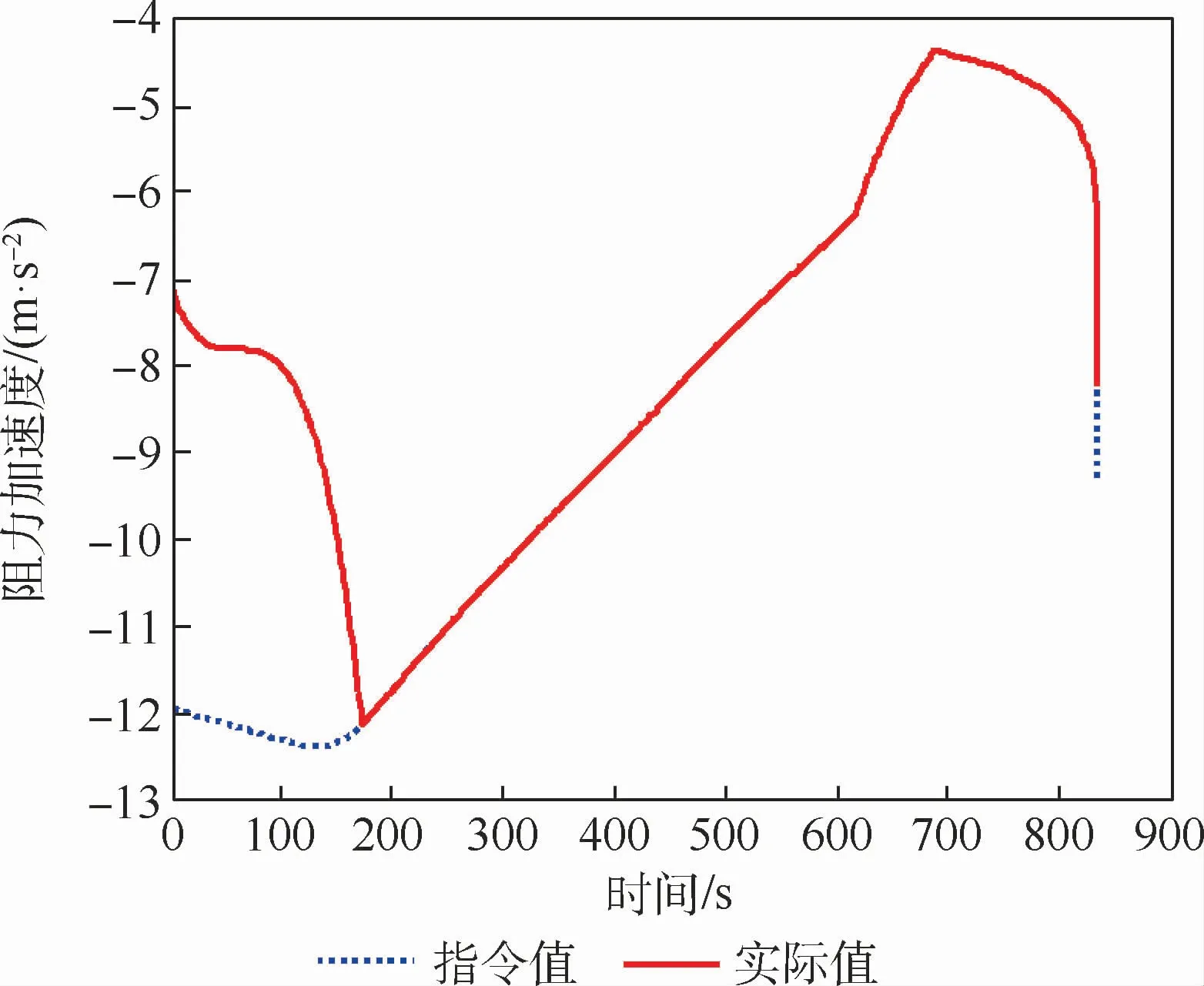
图16 阻力加速度曲线Fig.16 Drag acceleration curves

图17 升力加速度曲线Fig.17 Lift acceleration curves
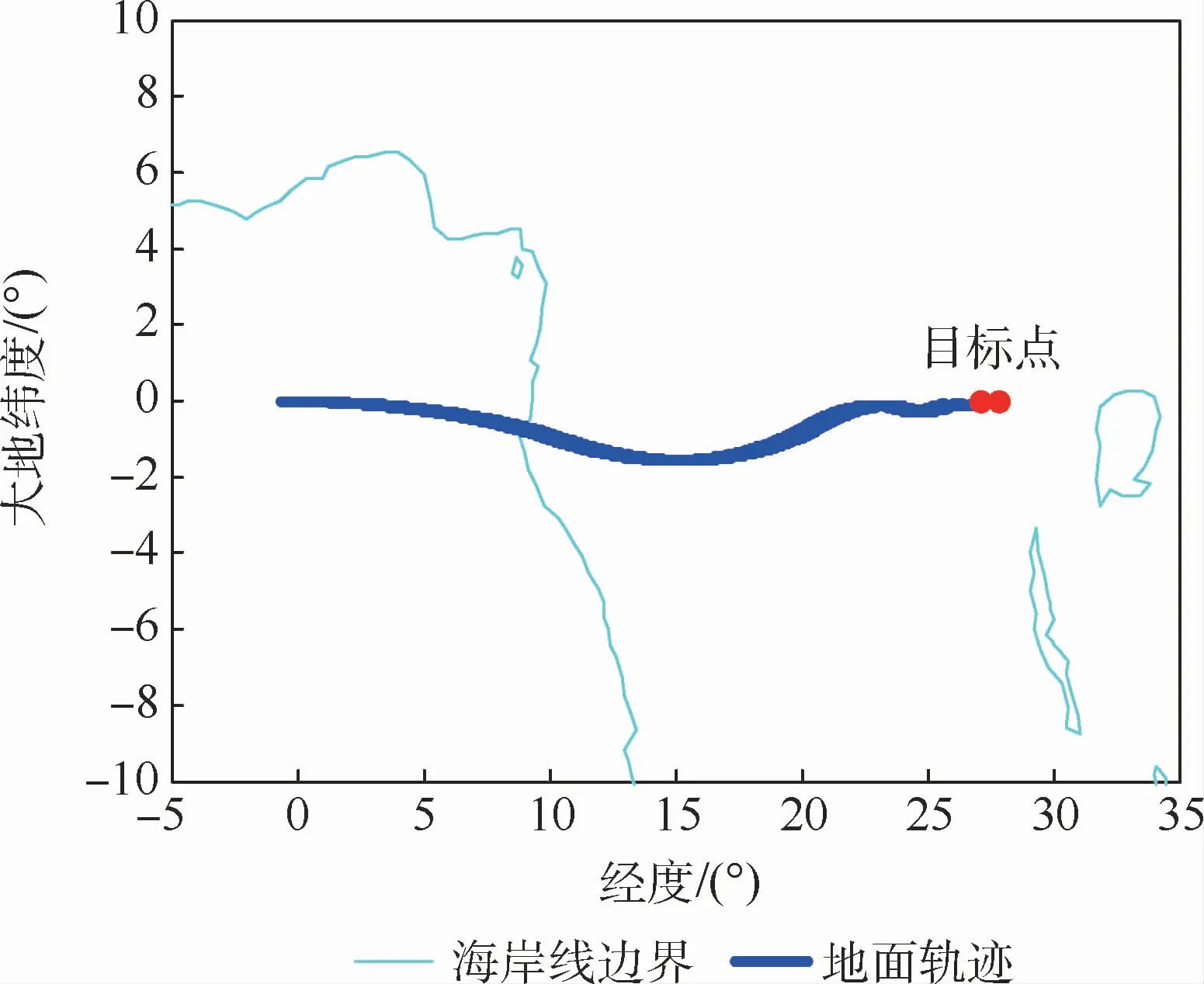
图18 地面轨迹Fig.18 Ground track
从图11和图12可见,约170 s前,倾侧角处于阻力加速度跟踪模式,此后倾侧角转入升力加速度跟踪模式。由图16可见,此期间实际阻力加速度与指令值曲线基本重合。由图17可见,升力加速度指令全程为正值,因此不需要采用大于90°的倾侧角进行跟踪,除了在倾侧角的阻力加速度跟踪模式和倾侧角反转过程中,其余飞行段航迹坐标系的实际升力加速度与指令值曲线基本重合。这说明由解析给出的阻力加速度指令和升力加速度指令在大部分飞行时间内尤其是后期能通过攻角和倾侧角得到有效跟踪。在飞行最末的十分之几秒时间加速度不能跟上指令是由比例导引的末端效应引起,对于制导精度影响很小。由图13~图15所示,动压、热流、过载约束均满足要求。另外,解析法在线生成的攻角和倾侧角制导指令剖面都比较平滑,且即使在倾侧角反转过程中飞行器的高度也不会出现明显跳跃。
6.4 蒙特卡罗仿真
为了验证本文方法对于不确定性的适应能力并评估控制精度,采用蒙特卡罗打靶方法进行仿真,选取的打靶仿真偏差项同文献[10],如表3所示。表中:ρ为大气密度。仿真过程中,上述误差在取值范围内随机选取。此外,还按高度施加了高空风场。高空风由南北向风和东西向风叠加而成,南北向风风速向北为正,东西向风风速向东为正。最大和最小风剖面如表4所示。蒙特卡罗仿真时,先根据高度插值得出最大、最小东西向风和最大、最小南北向风。根据2个随机数在最大值和最小值之间随机给出东西向风和南北向风的大小。

表3 蒙特卡罗仿真偏差项Table 3 Deviation term of Monte Carlo simulation

表4 高空风剖面Table 4 Upper wind pr ofile
蒙特卡罗打靶2 000次,终端参数散布频率直方图如图19~图26所示。

图19 终端速度散布图Fig.19 Scatter of terminal velocity

图20 终端高度散布图Fig.20 Scatter of terminal height
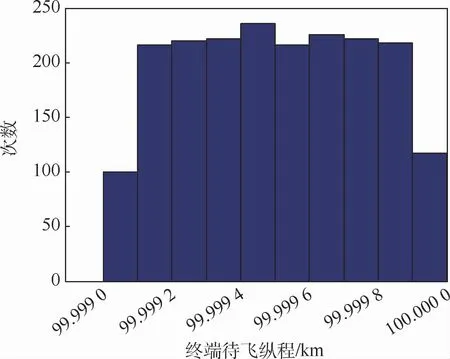
图21 终端待飞纵程散布图Fig.21 Scatter of terminal longitudinal range to go

图22 终端弹道倾角散布图Fig.22 Scatter of terminal trajectory inclination angle
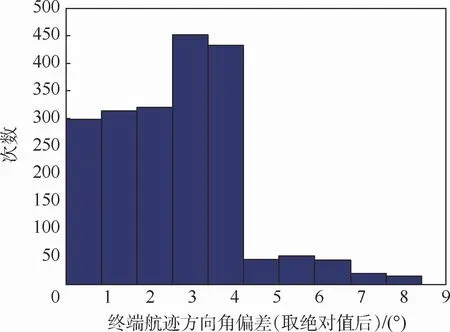
图23 终端航迹方向角偏差(绝对值)散布图Fig.23 Scatter of terminal azimuth deviation(absolute value)

图24 最大动压散布图Fig.24 Scatter of maximum dynamic pressure

图25 最大驻点热流散布图Fig.25 Scatter of maximum stagnation heat flow

图26 最大法向过载(本体坐标系)散布图Fig.26 Scatter of maximum normal overload(body coordinate system)
终端控制精度与文献[10]对比如表5所示。

表5 终端参数控制精度Table 5 Control accuracy of terminal parameters
可见,采用本文方法,对终端高度、终端速度的控制精度高于文献[10]。终端航迹方向角和终端弹道倾角的散布范围也小于文献[10]。由于本文方法以待飞纵程为迭代终止条件,纵向位置不存在误差。最大动压、最大热流、最大过载均满足约束要求。该方法与文献[17]类似,都具有不依赖参考轨迹和攻角剖面、计算量小等优点。
7 结 论
本文引入虚拟目标和伪视线角的概念,将比例导引应用于滑翔段,通过一维质点运动学解析并加权直接得到阻力加速度指令,利用阻力加速度和攻角的单调性关系实现有效跟踪,从而形成一种阻力和升力加速度指令在线快速解析与跟踪的制导方法。仿真表明:①本文方法对于终端速度、高度都可实现较高精度的控制,对终端弹道倾角也有一定的控制能力。②本文方法制导误差最大的参数是终端航迹方向角(或横向位置)偏差,其原因是:由于航向采用了基于侧向偏差走廊的bang-bang控制模式,受飞行器滚转通道姿态控制能力的制约,终端航迹方向角无法实现高精度控制。
若在接近终端时以侧向比例导引进行航向控制,可大幅提高终端航迹方向角(或横向位置)控制精度,但是这与终端速度控制不能兼顾,会以增大终端速度控制偏差为代价。在滑翔段制导中如何同时实现终端速度、高度、航迹方向角(或横向位置)的高精度控制仍有待于后续深入研究。
