基于有限时间引导律的欠驱智能船舶循迹控制

冯辉，胡胜，余文曌，*，徐海祥

（1.高性能船舶技术教育部重点实验室，武汉 430063； 2.武汉理工大学 船海与能源动力工程学院，武汉 430063）

在大数据和人工智能等新兴技术的影响下，研究无人化、绿色和安全的智能船舶已是大势所趋。作为智能船舶关键功能之一，智能航行受到了广泛的关注并得到了迅速的发展［1］。其中，循迹控制是实现智能航行功能的关键技术之一。

循迹控制是指控制欠驱智能船舶沿着一条预定的路径航行，并且这条路径与时间无关［2］。目前，国内外关于循迹控制的研究已有较多成果。Encarnação等［3］在Serret-Frenet坐标系中依据期望路径重新定义输出信号，将控制目标转化为位置误差和艏向角误差，但缺点是控制器的设计十分复杂。为了简化控制器的设计，有学者将循迹控制系统分为2个子系统：引导律和控制系统［2］。在获得路径信息和环境信息后，引导律计算出控制系统的输入信号，即期望艏向角；控制系统则产生相应的控制信号，使船舶的实际艏向跟踪引导律给出的信号，完成循迹控制目标。

LOS（line-of-sight）引导律［4］因其结构简单、收敛性好等优点而被广泛应用于循迹控制。但在实际运行环境中，船舶受到风浪流等环境因素的干扰，即横向环境力的作用，在循迹过程中会存在漂角。但欠驱动结构无法产生横向的控制力，因此船舶的实际运动轨迹将偏离期望的运动轨迹，限制了传统LOS引导律的应用。因此，如何减小漂角对循迹效果的影响是目前的研究热点。

减小漂角影响的一种最直接的方法就是测量漂角。文献［5］使用加速度计测量横向和纵向的加速度，再通过积分得到横向和纵向速度，进而计算出漂角，但缺点是加速度的测量值易受噪声的污染从而导致计算出的速度存在较大的误差。文献［6］利用全球导航系统计算漂角，但成本较高且精确性较差。另一种方法是利用积分LOS（ILOS）引导律。Børhaug等［7］针对传统LOS引导律无法抵抗环境干扰的问题，提出了一种应用广泛、具有积分作用的ILOS引导律，并证明了其全局一致渐进稳定性。文献［8-9］在Børhaug等［7］的基础上，在设计引导律时考虑了航速，简化了参数调整过程，但使得该算法的响应速度易受航速的影响。文献［10］针对直线接圆弧路径不连续问题提出了一种参数化ILOS引导律，使控制输出更加平滑，但引导效果易受期望路径插值的边界条件影响。文献［11］设计时变增益的ILOS引导律减小位置超调，但前向距离的上限和下限难以确定。文献［12］提出一种自适应ILOS（ALOS）引导律，将漂角视为固定参数，通过设计自适应项估计漂角。文献［13］在引导系统建模时考虑流速的影响，提出了一种直接ILOS引导律和间接ILOS引导律用以应对时变的海流，但无法应对其他未建模环境干扰的影响。文献［14］设计了一种降阶的扩张状态观测器，用来估计由外部干扰引起的时变漂角，但未考虑引导系统的有限时间稳定性。

近年来，有限时间控制方法因其更好的控制性能受到了广泛的关注，并得到了迅速发展［15］。文献［16］利用有限时间收敛的干扰观测器，以估计时变的大漂角，提高了曲线循迹的精确性。文献［17］提出了有限时间收敛的引导律，其不仅证明了漂角观测器的有限时间收敛性，还证明了位置跟踪误差的有限时间收敛性，但该方法的缺点是漂角的估计值易受传感器测量噪声的影响。

本文在现有国内外研究的基础上，提出了一种基于自适应控制理论的有限时间引导律，其控制参数可随横向偏差的变化而进行自适应调整，提升引导系统的响应速度，同时可适用于风浪流等环境载荷干扰下的欠驱智能船舶循迹控制，用于补偿船舶在循迹过程中受到的流载荷的干扰，并证明了该引导律的有限时间稳定性。通过仿真实现了欠驱智能船舶水平面内的直线和曲线循迹，并进行了仿真对比实验。

1 问题描述

1.1 船舶数学模型

欠驱船舶的水平面三自由度运动学和动力学方程如下［2］：

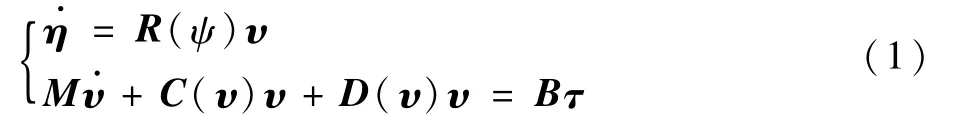
式中：η=［x，y，ψ］T为船舶在固定坐标系下的位置，x、y、ψ分别表示船舶在固定坐标系中的横坐标、纵坐标、艏向角；R（ψ）为坐标系旋转矩阵；υ=［u，v，r］T为船舶在运动坐标系下的运动速度，u、v、r分别表示船舶在运动坐标系中的纵向速度、横向速度、转艏角速度；M为包含水动力附加质量的惯性矩阵；C为包含附加质量的科里奥利向心力矩阵，由船舶自身和附加质量共同作用产生；D为阻尼系数矩阵；B为控制输入配置矩阵；τ=［τu，0，τr］T为控制输入矩阵，τu为船舶纵向推力，τr为转艏力矩。

因此，可以通过在式（1）的运动学和动力学方程中加入海流的速度，建立流载荷干扰下的船舶操纵运动方程，如下：

式中：υr=υ-Vc为船舶相对海流的速度。

1.2 有限时间稳定性

有限时间稳定是指系统状态能在有限时间内收敛到平衡点。考虑如下系统：

式中：x（t）表示系统状态；f：→Rn为包含原点的定义域 到n维空间Rn中的一个连续函数；0∈Rn表示零向量。

1.3 引导律

引导律的推导是在一个二维平面内完成的，其中，期望路径通常由一系列路径点（xp（θ），yp（θ））相连组成，如图1所示，其中θ为大于零的路径参数变量。图中：γp为期望路径上任意一点处的切线与正北方向的夹角，即Serret-Frenet坐标系与固定坐标系之间的旋转角。

假设在固定坐标系中，船舶的位置坐标为（x，y）。由图1可知，船舶在Serret-Frenet坐标系中的坐标为

图1 LOS引导律原理Fig.1 Geometrical illustration of LOS guidance law

式中：xe为纵向偏差；ye为横向偏差。

旋转角γp定义如下：

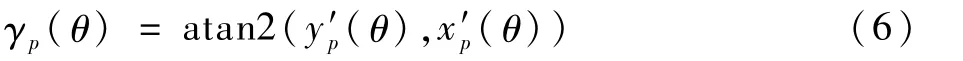
式中：x′p（θ）=∂xp/∂θ；y′p（θ）=∂yp/∂θ。

假设1 通常在直线或者直线圆弧循迹时，xe并不影响引导律的引导效果，为了简化计算，故假设xe=0。

假设3 船舶的实际艏向角可以准确跟踪期望艏向角，即ψ=ψd。

由式（5）和假设1可得

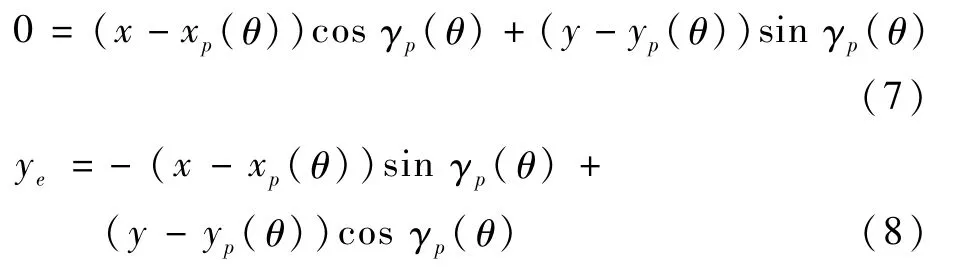
由式（1）可知船舶的运动学方程为

将式（9）代入式（8）得

注2 船舶在直线循迹或圆弧循迹时，漂角为一定值。但对于直线圆弧组成路径，漂角会发生缓慢的变化。因为漂角的动态特性变化慢于控制带宽变化，所以可通过自适应项估计漂角。

将式（10）展开，并结合假设2可得

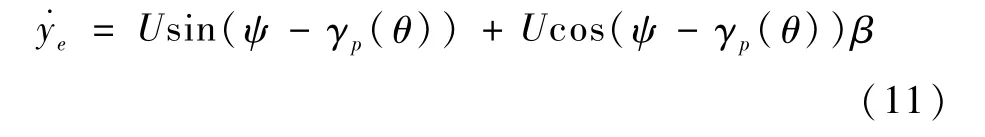
2 有限时间引导律

本文提出的有限时间引导律定义如下：

其中：参数k1＞0，k2＞0，参数0＜α＜1。

考虑到系统漂角β未知，建立如下误差跟踪系统：

定理1 对于系统（13），在满足假设3的前提下，设计的引导律（12）可以使系统（13）有限时间稳定，即

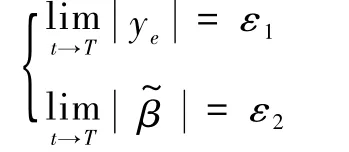
式中：ε1和ε2为大于零的极小常数。

证明 将式（12）代入式（11）中可得

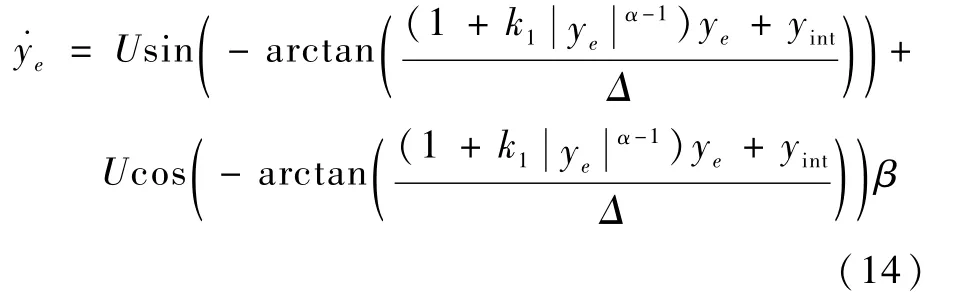
由于

将式（15）和式（16）代入式（14）得

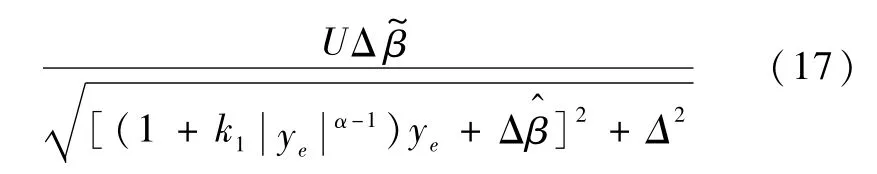
定义李雅普诺夫函数如下：

式（18）对时间求导并将式（17）代入可得

令

则式（19）可以改写为

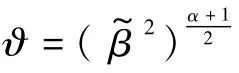
由文献［18］可知，存在参数0＜θ0＜1，满足：

得到

通过引理1可知，系统（13）是有限时间稳定的，并且收敛时间T1满足：

证毕

3 仿真实验

3.1 仿真条件

为了验证本文所提出的有限时间引导律的有效性，以武汉理工大学一艘欠驱智能船舶为模型进行了直线循迹仿真实验和曲线循迹仿真实验，并与文献［7］中的ILOS引导律进行对比分析，采用PID控制算法进行纵向和艏向控制器设计。

3.2 仿真结果与分析

1）直线循迹仿真

仿真条件设置如表1所示，引导律参数k1=1，α=0.8，k2=0.008。其他仿真条件如表1所示。

直线循迹的期望路径为连接表1中2个路径点的直线。图2为直线循迹航行路径曲线，图3为直线循迹横向偏差曲线。图2表示2种方法均能引导船舶沿期望路径航行。但是从图3中可以看出，本文引导律可以使ye更快地收敛至零且没有超调，大约在t=110 s时收敛至零；传统ILOS引导律的ye收敛速度较慢，大约在t=150 s时收敛至零。由此可知，本文引导律相比传统ILOS引导律在直线循迹时，ye的收敛速度更快，具有更好的引导效果。图4为比例系数kp随时间变化曲线。图5表示2种方法的实际艏向角都可以较好地跟踪期望值。

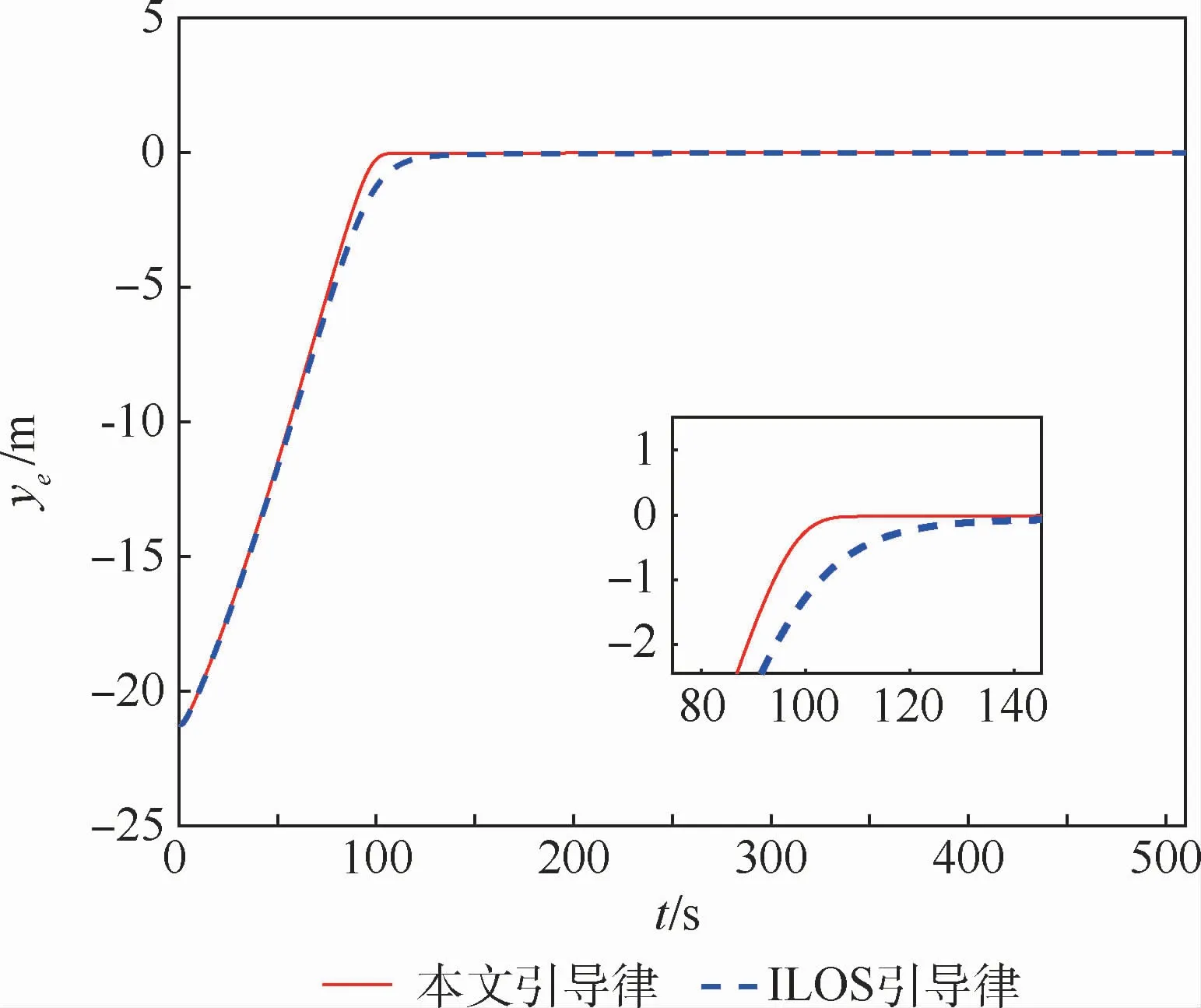
图3 直线循迹横向偏差曲线Fig.3 Curves of straight-line path following cross-track error

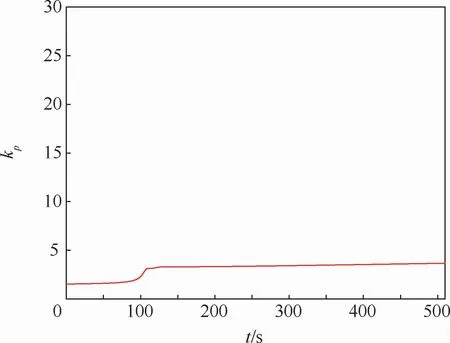
图4 直线循迹引导律比例系数变化曲线Fig.4 Curve of straight-line path following guidance law proportional coefficient

图5 直线循迹艏向角变化曲线Fig.5 Curves of straight-line path following heading angle

表1 直线循迹仿真条件Table 1 Simulation conditions of str aight-line path following

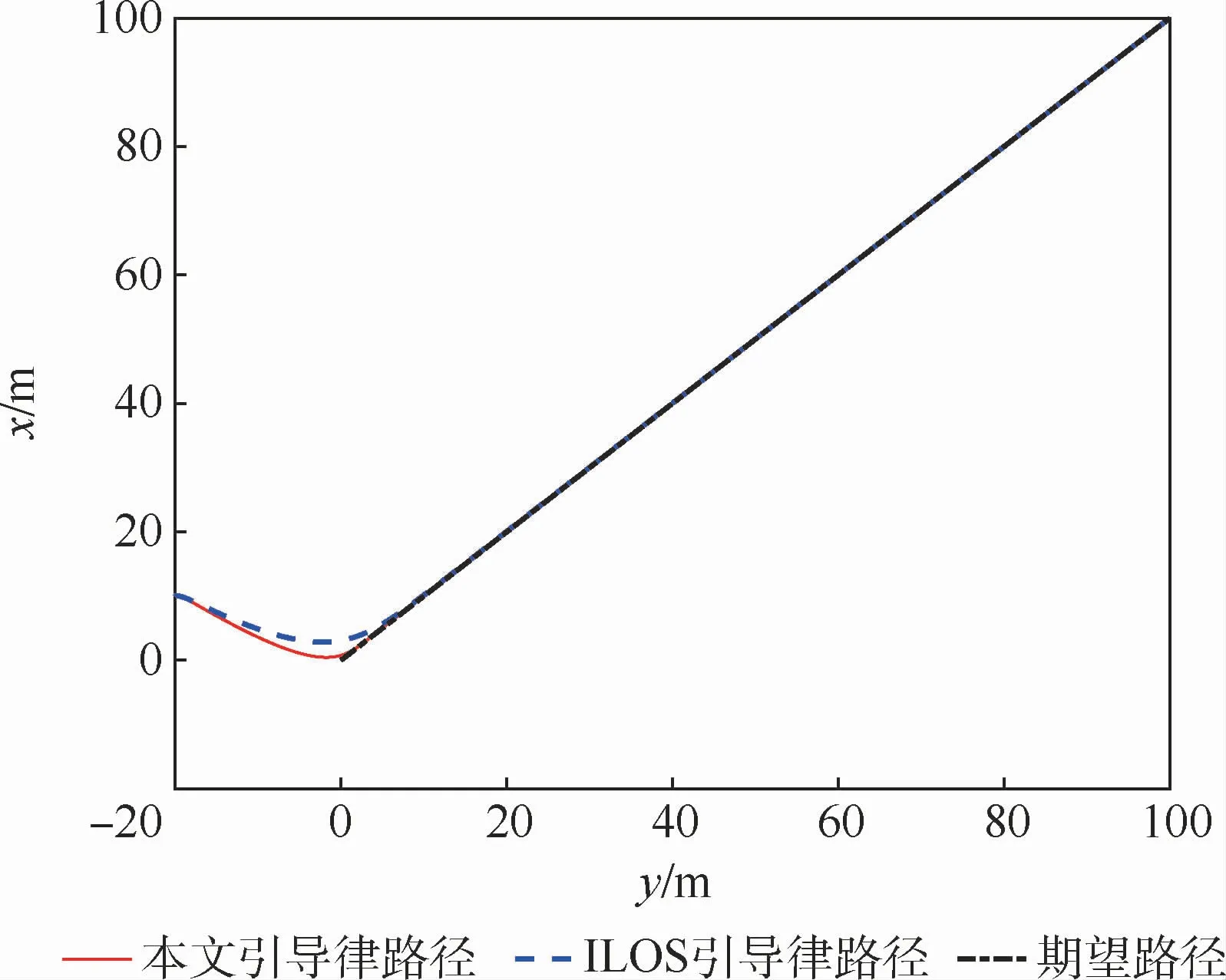
图2 直线循迹曲线Fig.2 Curves of straight-line path following

2）曲线循迹仿真

仿真条件设置如表2所示，引导律参数k1=0.4，α=0.8，k2=1。其他仿真条件如表2所示。曲线循迹的期望路径为连接表2中5个路径点的直线圆弧曲线。图6为曲线循迹航行路径曲线，图7为曲线循迹横向偏差曲线。图6表示2种方法均能引导船舶沿期望的曲线路径航行，但本文引导律的路径更接近期望路径。为了进一步比较2种方法引导效果的优劣，从图7中可以看出，本文引导律的ye收敛速度更快。在3处转弯路径处，ye由于曲率的增大而增大，本文引导律的ye的峰值分别为0.01 m、0.04 m和0.04 m，传统ILOS引导律的ye的峰值分别为0.03 m、0.3 m和0.3 m；本文引导律的ye重新收敛至零所花费的时间分别为148 s、127 s和127 s，传统ILOS引导律的ye又重新收敛至零所花费的时间分别为148 s、241 s和241 s。图8为比例系数kp随时间变化曲线。

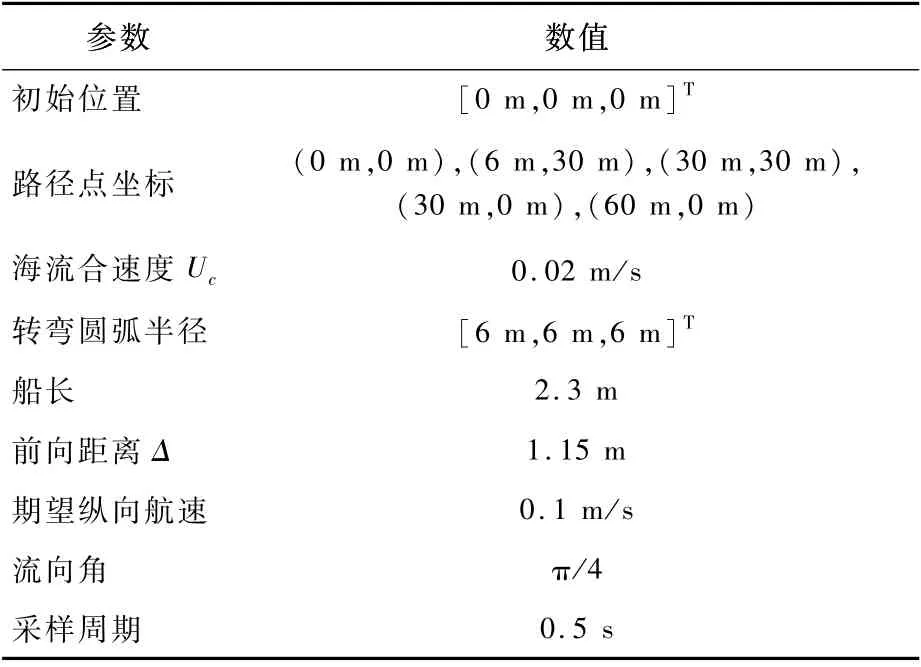
表2 曲线循迹仿真条件Table 2 Simulation conditions of curved-line path following

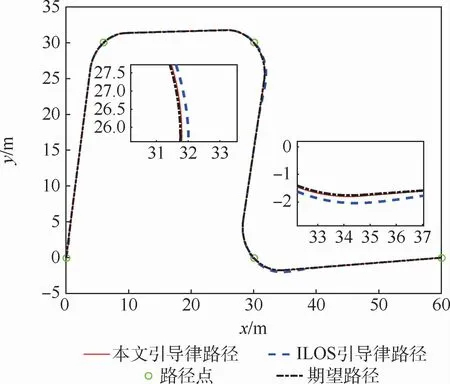
图6 曲线循迹曲线Fig.6 Curves of curved-line path following

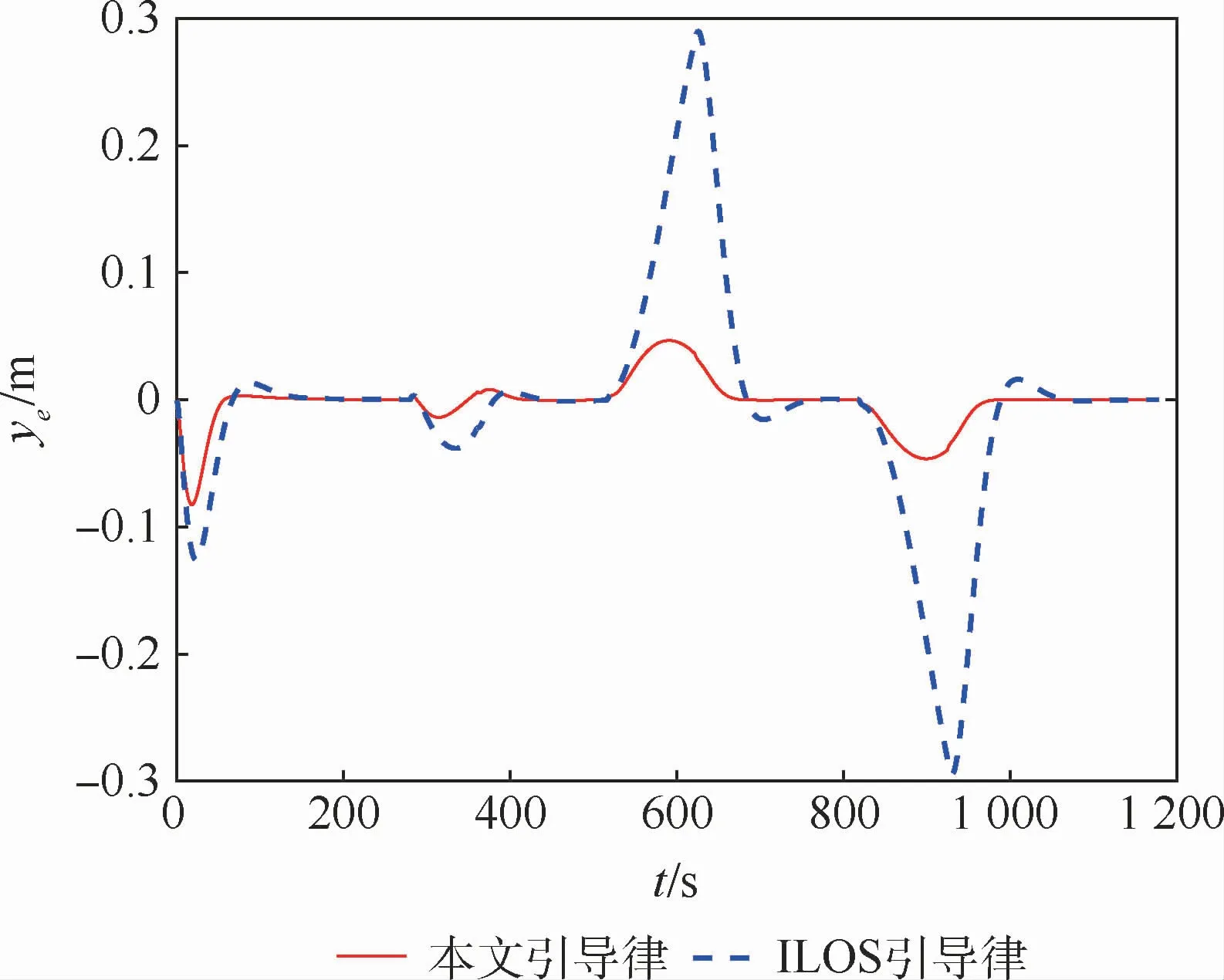
图7 曲线循迹横向偏差曲线Fig.7 Curves of curved-line path following cross-track error

结合图3和图4、图7和图8分析可知，比例系数随横向偏差的变化关系有大误差、小增益和小误差、大增益的特点。由图7和图8可知，当横向偏差稳定于零附近时，比例系数有较大的变化（如图中的80～280 s，448～515 s，697～816 s，997～1 175 s），原因是：横向偏差此时是一个逐渐趋近零的极小值，而比例系数对趋近零的极小值变化非常敏感，因此比例系数在此过程中变化较大。但由于横向偏差是极小值，当横向偏差趋于零时，比例系数的变化并不会影响引导效果。

图8 曲线循迹引导律比例系数变化曲线Fig.8 Curve of curved-line path following guidance law proportional coefficient

图9表示曲线循迹情况下，2种方法的实际艏向角也都可以较好地跟踪期望值。从图5和图9的艏向角对比曲线可以看出，在相同PID控制参数控制下，2种方法的艏向角跟踪效果都较好，但2种方法计算的期望艏向角不同，证明本文引导律计算的期望艏向角相比传统ILOS引导律更加合理和有效。

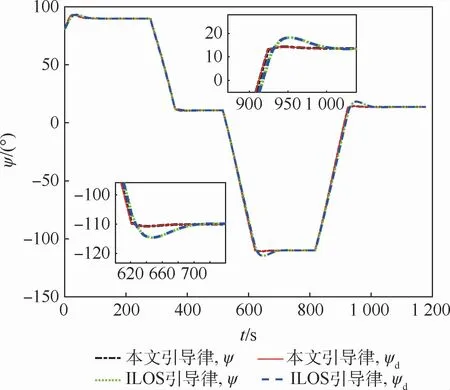
图9 曲线循迹艏向角变化曲线Fig.9 Curves of curved-line path following heading angle

4 结 论

经过理论分析和仿真对比实验，得到以下结论：

1）所提出的有限时间引导律适用于直线循迹和曲线循迹，设计的自适应项可以补偿环境干扰和路径曲率对循迹效果的影响。

2）基于有限时间稳定理论证明了漂角未知时，横向偏差控制系统在应用所提出的有限时间引导律时是有限时间稳定的。

3）通过直线循迹和曲线循迹仿真对比实验结果可知，相比于传统ILOS引导律，本文所提出的有限时间引导律可以使横向偏差更快收敛至零附近且超调量更小。

综上所述，对于欠驱智能船舶循迹控制，提出的有限时间引导律具有更大的应用潜力。本文未涉及控制器研究，但船舶运动受模型不确定和时变外部环境干扰的影响，将导致动力学控制性能变差，因此，下一步将研究模型不确定和时变外部环境干扰情况下欠驱智能船舶循迹控制器设计问题。