基于有效中转时间预测的不正常航班恢复技术

何坚，果红艳，，姚远，卞磊，*，唐红武，王殿胜

（1.北京工业大学 信息学部，北京 100124； 2.中航信移动科技有限公司，北京 100029）

航班计划表是航空公司提前几个月制定好的航班计划，包括每个航班的出发地、目的地、离港时间、到港时间及指定的执行飞机等信息。航班计划表的制定需考虑旅客的季节性、机组人员的排班、飞机的定期维护等多方面因素。在航空公司的日常运营中，飞机故障和恶劣天气造成的机场关闭、机场容量限制、空中交通管制等，都会导致航班不能按计划执行［1］。同时，飞机价格昂贵及其日常巨大的维护成本，使得航空公司尽可能地减少飞机闲置时间，以获得更大的利润。由于一个航班任务受到干扰后，会对其后续航班造成一系列的影响，为了减少航班计划受干扰带来的损失，航空公司需要及时修改航班计划表，重新安排飞机、机组等资源，不正常航班恢复问题由此提出。

航班恢复问题涉及8个必要因素：开始恢复时间、结束恢复时间、飞机、机场、航班、航线、干扰、航班中转时间。开始恢复时间是用户指定的开始进行航班恢复的时间，结束恢复时间一般是当日的24：00。在航班恢复过程中，飞机是执行航班任务的主体，飞机具有初始可用时间、初始可用机场、结束可用时间、结束可用机场、注册号等属性。恶劣天气可能会造成机场关闭的情况，机场关闭时禁止飞机到港、离港，只有在机场开启时进出该机场的航班才能正常执行。航班包括离港时间、到港时间、离港机场、到港机场、执行的飞机等多种属性。飞机执行的航班任务组成了该飞机的航线。航班恢复过程中包含多种干扰因素，如飞机故障、空中交通管制等。航班的中转时间是当前航班的离港时间减去前序航班的到港时间，在大多数航班恢复模型中，航班中转时间被设置成一个固定的常数。梁哲等［2］将30 min的固定中转时间应用到基于列向量生成算法的飞机恢复研究中。Yu等［3］将40 min的固定中转时间应用于时空网络模型中求解航班恢复问题。乐美龙等［4］将60 min的固定中转时间应用到基于贪婪随机自适应搜索过程的飞机优化恢复方案研究中。

固定的航班中转时间往往会影响实际恢复效果。本文的主要贡献在于引入了有效中转时间的概念。有效中转时间为特定的飞机在特定的时间、特定的机场、特定的天气状况下所需要的最短中转时间。在航班恢复过程中，根据航班的离港机场、到港机场、离港时间、天气及分配飞机的机型，使用LightGBM［5］方法预测该时间，替代原本的固定中转时间。在保证航班中转时间充足的前提下，减少航班中转任务中无意义的等待时间，提升飞机利用率。实际实验数据验证了有效中转时间在航班恢复问题中的有效性，降低了航班恢复的成本。将列向量生成算法与时空网络模型进行横向比较，验证了飞机数量较多的恢复问题中，列向量生成算法可以在更短的时间内，达到与时空网络模型近似的恢复效果。

1 研究现状

Teodorovic＇和Guberinic＇在 不 考 虑 航 班 取 消 的情况下建立模型，以减少乘客总延时为目标，采用分支定界法求解模型［6］，但示例只有3架飞机，缺少在大规模数据下的测试验证。Jarrah等［7］在只考虑航班延误或取消的情况下，以成本最小化为目标，加入了备用飞机及转移飞机的策略，提出由延迟模型、取消模型构成的时空网络模型，但该模型无法同时解决航班延误和取消的问题。Yan和Lin［8］以时空网络模型为基础，在机场关闭的情况下，提出将航班延误、航班取消及转移飞机等调度方法添加到一个框架中的调度模型。Cao和Kanafani［9-10］在Jarrah等［7］建 立 的 延 迟 模 型 基 础 上提出了0-1二次规划模型，能够同时包含航班延迟和航班取消。Thengvall等［11-12］针对机场关闭后的多机队飞机恢复问题，提出了基于多商品网络的3种模型。梁哲等［2］进一步改进了Thengvall等［11-12］的工作，提出了同时具有机场容量约束及维护灵活性的列向量生成算法。

虽然现有航班恢复模型已考虑了多方面的约束条件与恢复策略，但都没有考虑航班中转时间对航班恢复的影响［13-17］。航班中转时间是前一个航班到港后，下一个航班离港前飞机在机场停留的时间。现有不正常航班恢复模型中，通常将中转时间看作一个固定的常数［18-19］，而在实际中，由于天气、机场流量等因素影响，航班中转时间也是时刻变化的，固定的中转时间会造成部分航班在执行完中转任务后，需要等待一段时间才能离港，降低了飞机的利用率。对此，根据航班相关特征，对每个航班的有效中转时间进行预测。梯度提升树（gradient boosting decision tree，GBDT）模型［20］是常用的预测算法，但在大数据的情况下，GBDT模型训练速度相对较慢。LightGBM模型是GBDT模型的一种［21］，用于解决GBDT模型在海量数据处理上遇到的问题，其具有训练速度快、模型精度高的优点。Ke等［21］在多种数据集下实验证明，当模型的准确率相同时，LightGBM模型的训练速度是GBDT模型的20倍以上。因此，LightGBM模型被广泛应用于交通预测［22］、价 格 评 估［23］等 方 面。航 班 历 史 信 息 数 据量较大，选择使用LightGBM模型对航班的中转时间进行预测，将预测结果应用于不正常航班恢复模型中，通过列向量生成算法求解，生成新的航班计划。

2 基于LightGBM的航班有效中转时间预测模型

在分析影响航班中转时间主要因素基础上，建立基于LightGBM的航班有效中转时间预测模型及评估技术。

2.1 影响航班中转时间因素分析

航班的预计中转时间为当前航班的预计离港时间（estimated time of departure）与前序航班的预计到港时间（estimated time of arrival）之间的差值。为了有效预测航班的中转时间，选取了2018年5月至2019年10月某航空公司的实际航班数据进行特征分析。该数据集包含了不同机型、时间、位置及多种天气条件下的航班中转时间记录，具体特征如表1所示。影响航班中转时间的因素主要包括：

表1 数据结构特征Table 1 Data structure characteristics

1）机型因素。不同机型的飞机在执行航班中转任务时，需要完成的工作量不同。例如，座位数少的飞机在执行乘客登机、离机、装卸行李等任务时工作量较小，需要的时间较短。

2）离港机场因素。不同规模的机场每天航班起降架次有很大差异。2017年北京首都国际机场航班日高峰达到1 863架次，而长沙黄花国际机场仅有548架次。机场的繁忙程度会体现在航班起降架次上，机场繁忙时，可能会出现跑道被占用等资源不足的情况，航班只能在地面等待，中转时间随之增加。

3）到港机场因素。航班到港机场与离港机场之间的距离可能影响航班执行中转任务的工作量，对中转时间造成影响。

4）天气因素。当天气条件不佳时，为了保证飞行安全，可能会导致航班延误，造成航班的中转时间增加。

5）时间因素。图1表示了数据集中2018年5月至2019年5月每个月的离港航班总数。不同月份离港航班数有明显的波动。将2018年5月2日的航班数据以1 h为时间间隔分成24个时间段，每个时间段的离港航班个数如图2所示，10：00—21：00之间，离港航班数量明显多于其他时段。航班的时间因素与机场的起降架次相关，会对航班的中转时间造成影响。此外，初始航班计划会对航班的中转时间造成影响。例如，某架飞机计划到港时间为09：00，该飞机执行的下一趟航班将于17：00离港，该航班的中转时间为480 min，这种数据会影响航班中转时间的预测。因此，对所有的航班数据进行预处理，将航班中转时间偏大的数据剔除，只保留中转时间在30～75 min之间的样本。筛选后的数据集包含12万条航班信息。

如图1和图2所示，航班的中转时间与离港时机场的流量紧密相关。在不同的月份或同一天的不同时间段内，航班的离港数量存在较大差异。因此，对原始数据集进行处理，提取到航班离港的月份、时间段数据。依据上述航班中转时间影响因素，选取航班的离港机场、到港机场、机型、离港时间段、离港月份、天气信息作为影响航班中转时间预测模型的特征。

图1 离港航班个数与月份关系Fig.1 Relationship between the number of departure flights and the months

图2 2018年5月2日离港航班个数与时间关系Fig.2 Relationship between the number of departure flights and the time on May 2，2018

此外，针对原始数据集中存在数据缺失、数据重复问题，对原始数据进行缺失值填充、去重操作，对出发机场及到达机场通过mapping方式将类别信息映射成数值，再将机型、雪雨等天气信息使用独热编码（one-hot encoding）转换成数值信息。

2.2 基于LightGBM的航班有效中转时间预测

采用LightGBM模型对航班的中转时间进行预测，LightGBM采用具有深度限制的按叶子生长（leaf-wise）策略，能够提升模型的精确度，降低过拟合的风险；同时，该模型使用直方图算法，大幅度减少了内存占用、执行时间。

将2018年5月至2019年7月的9万条数据作为训练集，将2019年8月至10月的3万条航班数据作为测试集。提取的特征如2.1节所述，预测目标为航班的中转时间，属于连续值的预测问题，这类问题属于机器学习中的回归问题。模型的性能使用均方根误差（root mean square error，RMSE）及平均绝对误差（mean absolute error，MAE）来衡量，计算公式如下：

采用相同的特征，将LightGBM模型与GBDT模型进行实验对比，实验结果如表2所示。Light-GBM模型的RMSE及MAE这2个评估指标均优于GBDT模型，并且LightGBM模型的训练时间小于GBDT模型。

表2 不同模型航班中转时间性能对比Table 2 Performance comparison about different models’flight transit time

3 基于列向量生成算法的不正常航班恢复

基于第2节航班中转时间预测模型，预测出恢复期内所有航班被任意飞机在整点时刻执行时的中转时间。设计了基于列向量生成算法的不正常航班恢复算法，在每次使用航班中转时间时，根据航班执行的整点时刻、天气、离港机场、到港机场、执行任务的飞机等信息，从航班中转模型的预测结果中读取该航班的中转时间，作为有效中转时间。

3.1 基于列向量生成算法的不正常航班恢复算法

系统为每一航班设定最大许可延误时间，据此可采用航班延误、航班取消、航班交换3种策略实现不正常航班恢复。其中，当航班的延误时间小于该数值，航班允许延误，可以使用航班延误的策略来降低航班恢复方案的成本；当航班的延误时间超过该数值，航班通常会被取消，将飞机资源留给其他航班使用；在航班恢复过程中，可采用同类型飞机相互替代的方法（即航班交换策略）来设计恢复方案。此外，航班恢复过程受到可用飞机数量和机场运行、关闭状态的影响。考虑飞机故障、机场关闭的情况，设计基于列向量生成算法的低成本航班恢复方案。

基于列向量生成算法的不正常航班恢复算法的流程如图3所示。该流程主要分成4个阶段：初始化过程、主问题的求解、子问题的求解及生成恢复方案。在初始化过程中，为每个飞机选择执行的航班序列，形成飞机的航线；在主问题中以恢复成本最小化作为目标，建立整数规划模型，并计算其松弛模型，为每个飞机选择执行的航线；在子问题中，为飞机选择恢复成本更低的航线加入主问题的航线选择集合中，主问题与子问题迭代执行，直到所有飞机的子问题都无法找到比当前主问题选中航线更优的航线，迭代过程结束；计算主问题的整数规划模型，根据模型选中的航线，生成航班恢复方案。

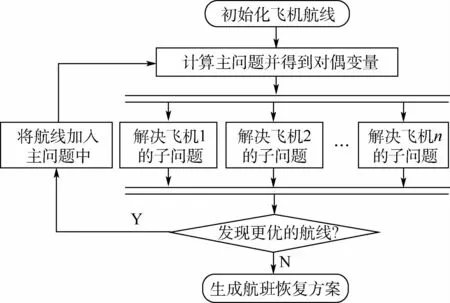
图3 列向量生成算法解决不正常航班恢复问题的流程Fig.3 Flowchart for solving irregular flight recovery problems by column vector generation algorithm

为了清晰描述航班恢复问题的过程，定义以下几类符号：

1）集合。可用飞机的集合P，航班的集合F，航线的集合L，机场的集合A。

2）参数。航班f取消的成本cf，飞机p执行航线l的成本cp，l，航班f属于航线l时bf，l值为1，否则bf，l值为0，航线l终止于机场a时bl，a值为1，否则bl，a为0，航班f原计划由飞机p执行时sp，f值为0，否则sp，f为1，恢复期结束时机场a需要的飞机数量ha，换飞机个数上限sp，恢复期结束后任何机场中每个飞机不平衡的成本cub；恢复期结束后所有机场不平衡的飞机个数numub（参数cf、cp，l、ha、sp、cub、numub均大于0）。

3）决策变量。如果飞机p执行了航线l时xp，l值为1，否则xp，l值为0，如果航班f被取消时yf值为1，否则yf值为0。

基于上述符号，建立如下航线选择整数规划模型：

航班恢复过程以成本最小化为目标，如式（3）所示，恢复成本包含取消航班的成本及执行航班的成本。恢复过程主要考虑如下约束：式（4）为航班覆盖约束，表示每个航班只能执行一次，或者取消该航班；式（5）为飞机任务约束，表示每个飞机最多只能执行一条航线；式（6）为机场的飞机流平衡约束，恢复期结束时，各个机场停靠的飞机个数应该等于恢复期结束后待执行航班需要的飞机个数；式（7）表示在主问题的计算结果中，所有飞机选中的航班集合内，换飞机的航班个数之和不能超出限制个数；式（8）和式（9）表示决策变量的取值约束。

3.2 航班恢复算法的初始化过程

航班恢复过程中，初始化过程的目的是为主问题中飞机航线提供初始的选择方案。实验分析发现，列向量生成算法的初始解会对算法的迭代次数产生很大影响。当初始解足够好时，列向量生成算法可经过几次迭代就得出最终恢复方案。对此，采用初始化原始航线的方法为每架飞机生成一条初始航线，步骤如下：

步骤1 以飞机注册号、计划离港时间对航班进行排序；根据航班的状态（航班执行中、航班未离港、航班已到港）、航班预计飞行时长、机场的状态（机场开启、机场关闭）及飞机的状态（飞机正常、飞机故障）计算每架飞机在恢复期内的初始可用时间、初始可用机场。

步骤2 从飞机集合中选出一架飞机，若飞机正常，执行步骤3，若飞机故障，执行步骤4。

步骤3 遍历飞机的初始飞行计划，根据飞机所在机场、可用时间、离港机场、到港机场的状态信息选出飞机执行的下一个航班任务，更新该飞机的可用时间及机场信息，遍历完该飞机执行的所有航班之后，将该飞机从飞机集合中删除，并将航线加入到航线集合中。

步骤4 查看飞机的可用时间，若飞机在整个恢复期内都不可用，则该飞机的航线为空；若飞机在恢复期内一段时间内不可用，只能在飞机的可用时间安排航班任务。

步骤5 继续执行步骤2，直到飞机集合为空，初始化过程结束，每个飞机都得到一条初始航线。

3.3 航班恢复算法的主问题

航班恢复主问题的求解过程就是飞机航线的选择过程，属于整数线性规划问题。航班恢复主问题的整数规划模型在3.1节中已经说明。模型的目标函数如式（3）所示，模型以恢复成本最小化为目标。在主问题的计算中，需要考虑多种类型的约束，式（4）～式（6）均为主问题求解的物理约束。此外，提出航班恢复实际业务中对换飞机总个数的业务条件约束，如式（7）所示。梁哲［2］和Yu［3］等都没有此类型的约束，但在航班实际运行中，这样的约束是必要的，也是符合航空公司具体操作规范的。解决不正常航班恢复问题的流程如图4所示，图中展开说明了主问题的计算流程，在计算主问题的整数型性规划时，需要构建物理约束（式（4）～式（6））、业务条件约束（式（7））及决策变量约束（式（8）、式（9）），并根据可行航线集合生成恢复方案。

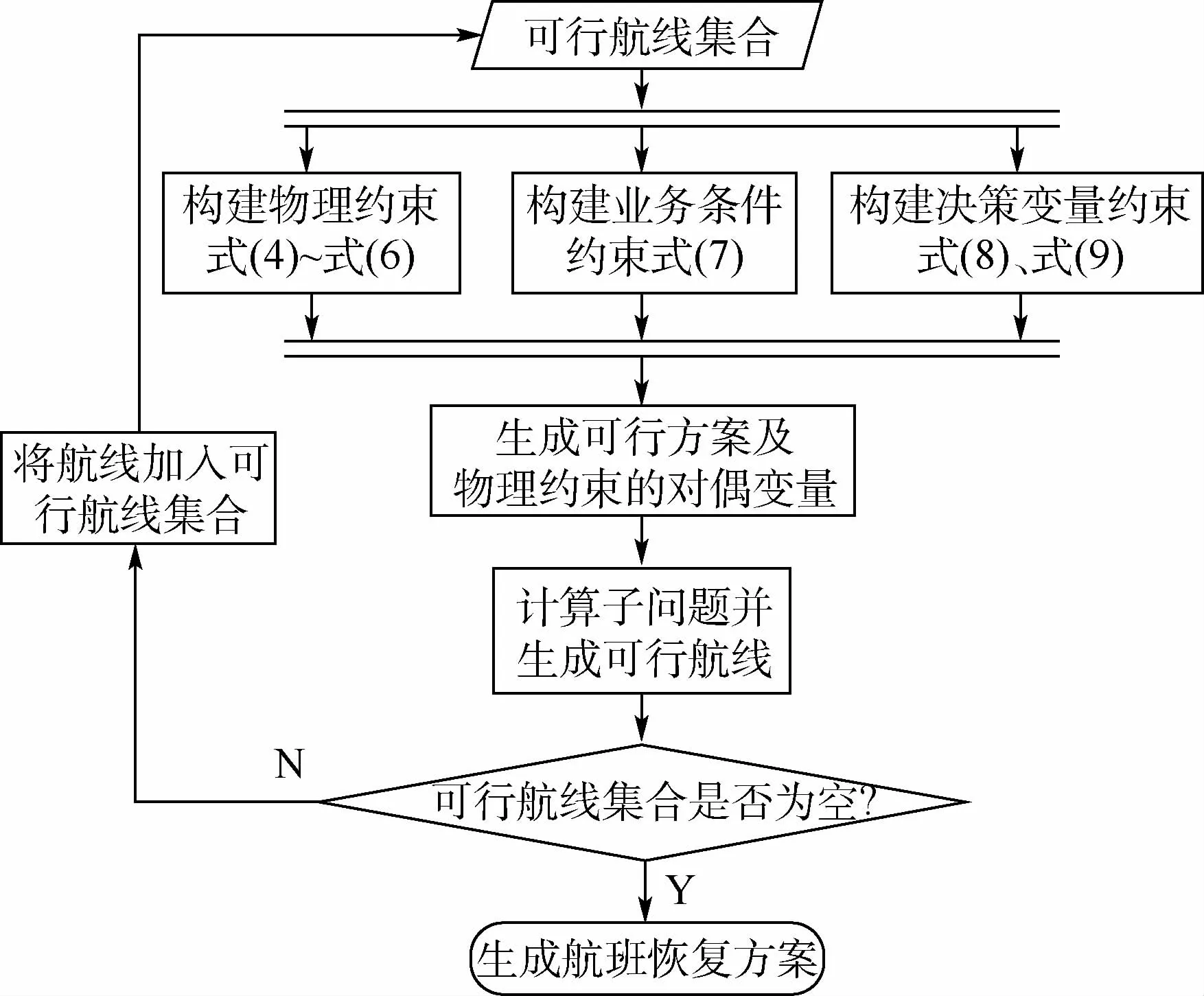
图4 列向量生成算法主问题的流程Fig.4 Flowchart of main problem using column vector generation algorithm

在实际应用中，式（6）的飞机流平衡约束可能造成模型无解。因此，可以去掉此约束并采用式（10）在目标函数中增加飞机不平衡成本因子来修正式（3）。

为了使用列向量生成算法计算航班恢复问题，对主问题的整数线性规划模型进行线性规划松弛，将约束条件式（8）和式（9）替换为式（11）和式（12）的非整数约束，建立松弛模型。

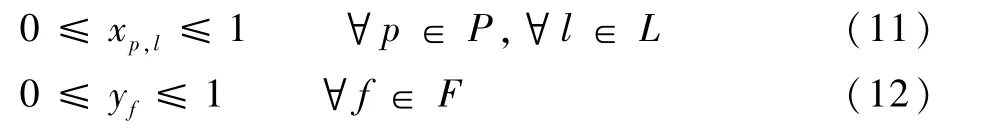
3.4 航班恢复算法的子问题

子问题的任务是计算每个飞机的所有可行航线的简约成本，从而选择出成本最优的解。如图5所示，图中展开介绍了子问题的处理流程，在子问题的计算中，仅需要考虑主问题中物理约束带来的影响。令αf表示式（4）中对于航班f的对偶变量，令βp表示式（5）中对于飞机p的对偶变量，令γa表示式（6）中对于机场a的对偶变量，飞机p执行航线l的简约成本¯cp，l按照式（13）计算：

图5 列向量生成算法子问题的流程Fig.5 Flowchart of subproblem using column vector generation algorithm

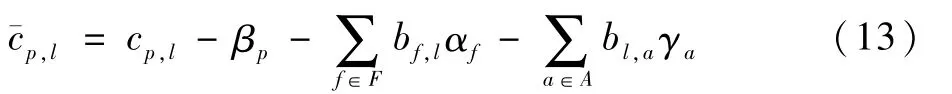
飞机p执行航线l的成本cp，l根据式（14）计算：

飞机p执行航线l时的平均航班简约成本meanp，l按照式（15）计算：

为了筛选出飞机的最优可行航线，应计算出飞机p所有航线的简约成本的最小值minc，p及整条航线上所有航班的平均简约成本的最小值minmeanc，f，按照式（17）、式（18）计算：

若minc，p＜0，则飞机p选中的航线l优于该飞机在主问题中选中的航线；若minc，p≥0且minmeanc，f＜0，则飞机p选中的航线l优于该飞机在主问题中选中的航线；若minc，p≥0且minmeanc，f≥0，则飞机p的最优航线就是主问题中选择的航线。

使用列向量生成算法进行航班恢复的步骤如下：

步骤1 生成航班恢复初始解，将初始解加入主问题的航线集合R中。

步骤2 根据R计算主问题的线性模型，得出计算结果及对偶变量αf、βp、γa，并根据每个选中航线的总成本及选中航线上的总航班数，计算出每个选中航线上所有航班的平均航班成本¯cp。

步骤3 根据航班计划的预计离港时间、预计到港时间计算出所有航班的计划执行时间。根据飞机的可用时间、飞机的可用机场、机场的可用时间、航班的预计离港时间、航班的计划执行时间这些信息，并且将恢复期开始时间、恢复期结束时间作为航线的限制信息，控制航线的长度，使用枚举法，为所有飞机生成全部可行航线集合S。

步骤5 若集合C中存在航线，将C中的所有航线加入集合R中，执行步骤2；若C为空集合，则执行步骤6。

步骤6 根据主问题的整数规划模型，计算出整数解。

步骤7 根据步骤6中的整数解，生成新的航班计划表。

4 实验及结果分析

采用JetBrains PyCharm 2019对本文算法进行了编程实现。算法运行在Win10操作系统，运行内存为32 GB，并使用大规模数学规划优化器Gurobi求解主问题的线性规划及整数规划模型。

实验数据均来自于航旅纵横APP官方平台（http：//www.umetrip.com/），其计算及数据可为航班运控、航延服务、疫情防控［24］等提供精准服务。数据按航班规模分为5组，航班个数分别为50、100、200、400、800，飞机个数分别为19、37、71、144、305，算例中给出了离港、到港涉及机场的总和。算例中存在飞机故障及机场关闭的情况，恢复期内涉及的航班个数及机场个数、飞机故障个数等信息如表3所示。表4为每个算例的成本参数。

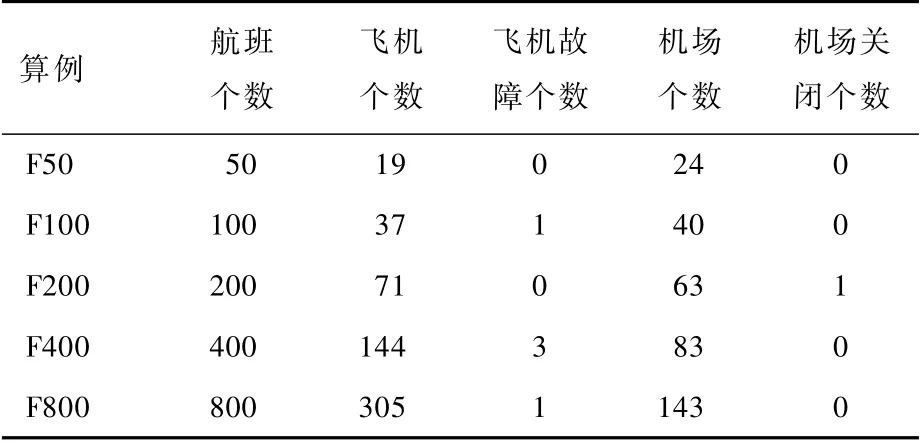
表3 算例基本参数Table 3 Basic par ameters of calculation examples

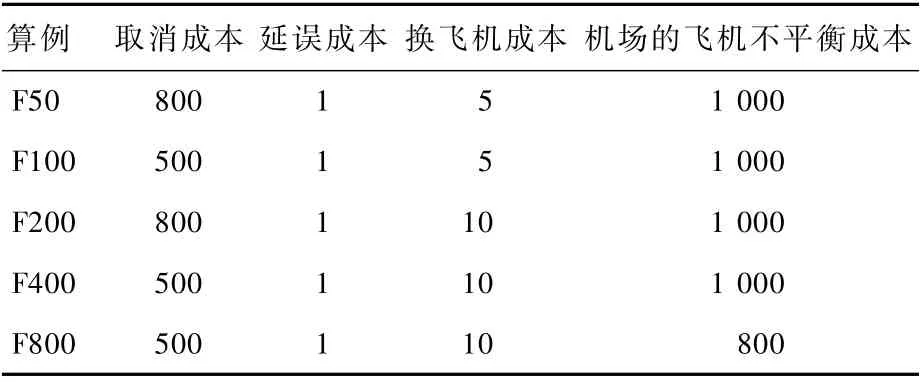
表4 算例成本参数Table 4 Cost parameter s of calculation examples

实验选择以时空网络模型的恢复结果作为对照，将时空网络模型的恢复结果与改进后的列向量生成模型恢复结果进行比较。其中，未使用有效中转时间的时空网络模型及未使用有效中转时间的列向量生成模型分别记作模型A及模型B，2个模型的恢复结果如表5、表6所示。使用了有效中转时间的时空网络模型及使用了有效中转时间的列向量生成模型分别记作模型C、模型D，2个模型的恢复结果如表7、表8所示。

表5 模型A的计算结果Table 5 Calculation r esults of Model A

表6 模型B的计算结果Table 6 Calculation results of Model B

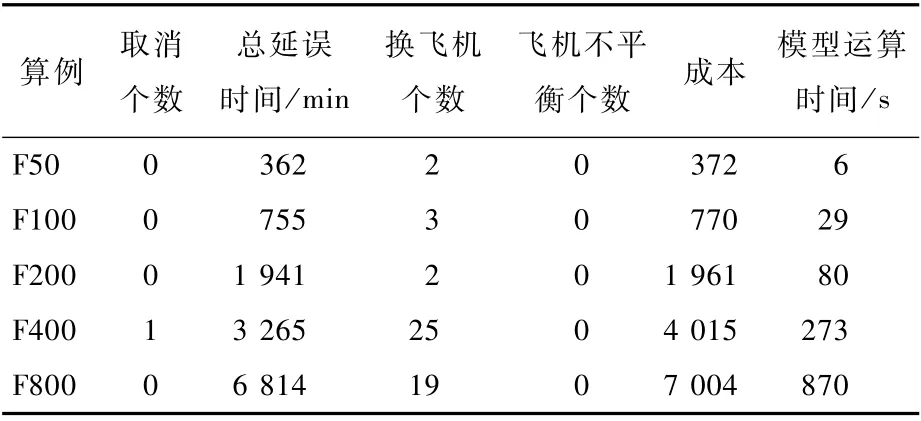
表7 模型C的计算结果Table 7 Calculation results of Model C

表8 模型D的计算结果Table 8 Calculation results of Model D

将算例F800（航班数800）作为样本，航班的中转时间分布情况如表9所示，表中包含设置的固定中转时间及在当前中转时间下能够完成中转任务的航班比例。当固定中转时间为30 min［2］时，没有航班能够完成中转任务，当固定中转时间为40 min［3］与60 min［4］时，大多数航班不能完成中转任务，当固定中转时间为75 min时，63.15%的航班能够完成中转任务。因此，选取75 min作为固定中转时间，应用到模型A、模型B中。所有算例的换飞机个数限制在30架内，时空网络模型采用30 min［3］的时间窗口。上述3个模型的恢复成本包括航班延误成本、航班取消成本、换飞机成本及机场的飞机不平衡成本4部分。通过恢复结果的对比可以发现，应用了有效中转时间的列向量生成模型（模型D），能够取得最小的恢复代价。同时，与时空网络模型相比，列向量生成算法在运行时间上有很大的优势。模型A、模型B在不同航班规模下的运行时间如图6所示。随着算例规模的增加，列向量生成模型运行时间的增长速度远小于时空网络模型。

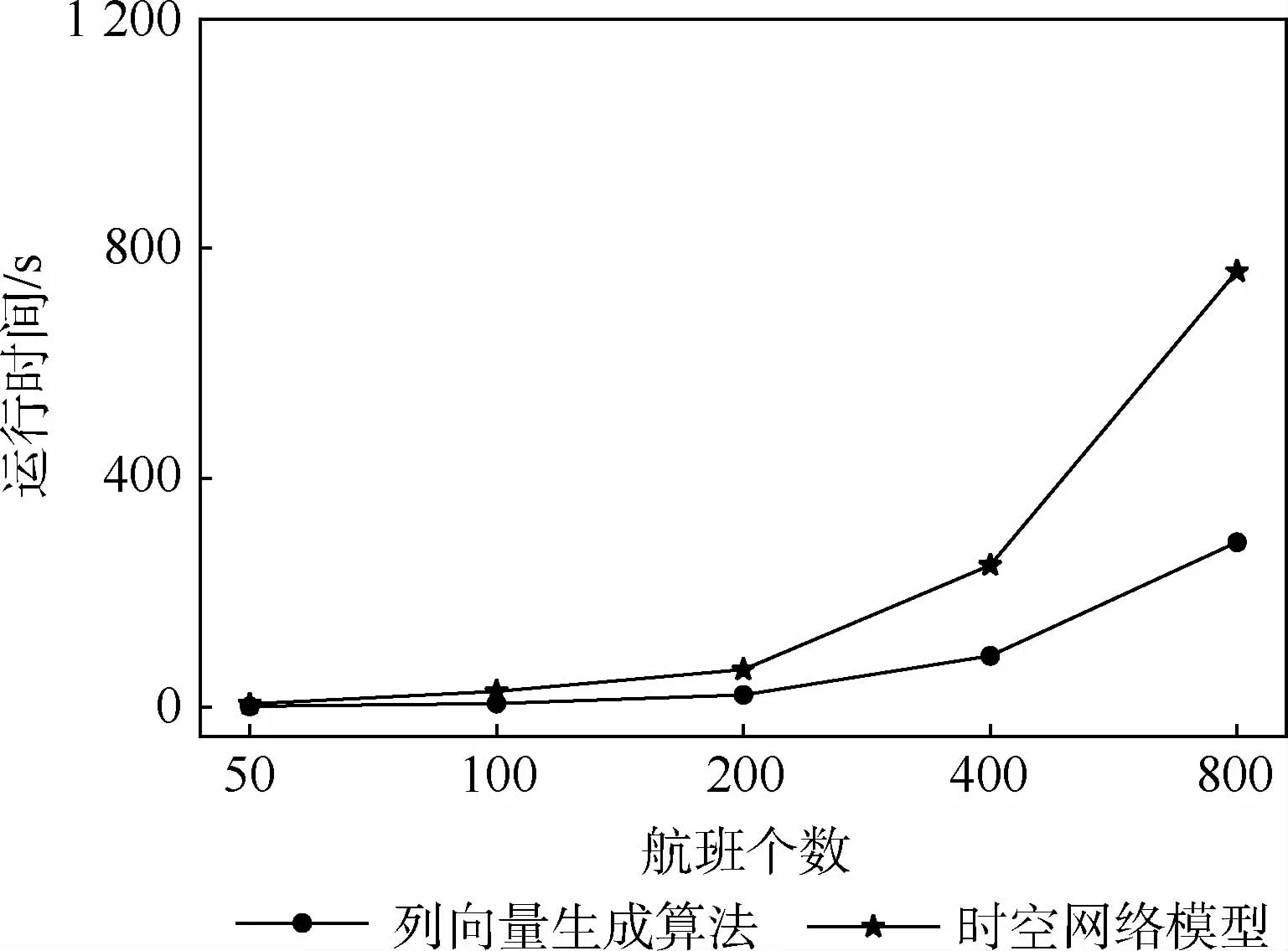
图6 列向量生成算法与时空网络模型运行时间对比Fig.6 Comparison of operation time between column vector generation algorithm and spatio-temporal network model

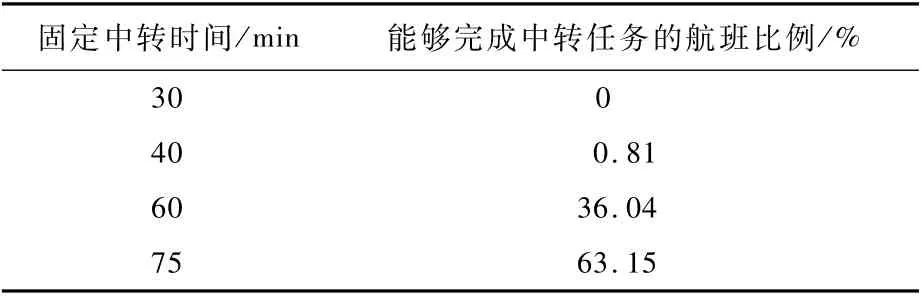
表9 算例F800的航班中转时间分布Table 9 Flight transit time distribution of scenario F800

模型D使用Gurobi优化器对主问题的求解结果如表10所示。其中，LP为迭代结束时主问题线性规划模型的最终计算结果，IP为主问题整数规划模型的最终计算结果，最优间隔比例由式（19）计算得出。模型D的4个算例的最优间隔比例均为0%，取得了最优解，算例F400没有取得最优解，但是该算例的最优间隔比例仅为0.059%，证明了列向量生成算法的有效性。

表10 基于模型D的优化器实验结果Table 10 Experimental results of optimizer based on Model D

对比表5和表6，由于时空网络模型是采用将所有的航线直接进行优化计算的方式，航线个数随着航班规模的增长迅速增加，使得模型在求解大规模问题时计算速度非常慢。列向量生成算法采用迭代的方式选择航线，使得每次迭代过程的计算量都远小于时空网络模型，并且列向量生成算法可以通过控制迭代次数的方式在有限的时间中求得最低的恢复成本。时空网络方法采用离散的航班延误时间，在某个时间间隔内，航班未能执行，只能在下一个时间间隔才可能离港，离散的延误时间可能会导致模型求出的最小成本高于最优解的最小成本。而列向量生成算法采用连续的航班延误时间，飞机可用时就可以分配飞机离港，解决了这一问题。同时，时空网络模型需要将时间轴划分成多个相同长度的时间窗，时间窗口的长短不易控制，如果时间窗口较长，时空网络模型求得的恢复成本会偏高，而时间窗口较短，模型的恢复成本会降低，但是模型的求解时间会更久。列向量生成算法采用连续的延误时间，不需要考虑这一问题。通过对比列向量生成算法及时空网络模型的恢复结果，列向量生成算法存在恢复成本高于时空网络模型的情况，若列向量生成算法在筛选满足子问题约束的航线时没有遗漏，则列向量生成算法可以取得与时空网络模型相同或者更低的恢复成本。由此可知，列向量生成算法筛选满足子问题约束的航线，并加入到主问题的优化集合中，这一特点使得列向量生成算法在计算最优解时，可能遗漏最优解中包含的航线。列向量生成算法的这一特点及时空网络模型的时间窗口较长都可能导致模型求得的恢复成本比最优恢复成本高，因此时空网络模型与列向量生成算法各有优劣。但是在大规模航班恢复过程中，2个模型的恢复成本相似时，时空网络模型的计算时间可以达到列向量生成算法的3倍以上，影响了恢复结果的实时性。因此，在计算大规模航班恢复问题时，列向量生成算法的优势明显。表7、表8显示了将航班有效中转时间预测模型分别应用到时空网络模型和列向量生成算法中的航班恢复结果，与表5、表6相比，虽然模型的运行时间可能稍有增加，但是2个模型的恢复成本均有显著的下降。

5 结 论

将航班中转时间预测模型与改进后的列向量生成算法相结合，提出了一种基于有效中转时间的不正常航班恢复模型。通过对比实验，得出以下结论：

1）基于列向量生成算法的航班恢复模型与时空网络模型相比，在恢复成本基本一致的情况下，计算时间更少。并且随着航班规模的增加，在时间上的差异会进一步增大。当航班规模是400架时，时空网络模型的恢复时间是列向量生成算法的2.97倍；当航班规模是800架时，时空网络模型的恢复时间是列向量生成算法的3.67倍。

2）将有效中转时间应用于不正常航班恢复模型，虽然模型的计算时间有所增加，但航班的恢复成本明显降低。在大规模恢复场景下，可以将航班恢复成本减少36.3%。

不正常航班恢复问题涉及到飞机恢复、机组恢复、乘客恢复3个阶段，本文中只针对飞机恢复阶段进行了研究，下一步可以针对后2个阶段进行研究，逐渐完善所提出的不正常航班恢复模型。在飞机恢复问题中，只考虑了以恢复成本为目标的航班恢复问题，在未来的研究中，可以将航班恢复成本与航班正常率等多个目标同时添加到航班恢复模型中，实现多目标条件下的航班恢复模型。