应用GWR估算贵州省表层土壤全钙空间分布

黎 喜， 杨胜天，*， 罗 娅， 李超君， 张 军， 吴习锦， 张宇嘉， 潘子豪

(1.贵州师范大学 地理与环境科学学院， 贵州 贵阳 550025； 2.北京师范大学 水科学研究院， 北京 100875)

贵州省(24°30′～29°13′N，103°31′～109°30′E)地处中国西南腹地，位于云贵高原，平均海拔为1 100 m，地形整体呈现为西高东低，常年气候温暖湿润，年均降水量在1 100～1 300 mm，年均气温为14.8℃，全省面积的97.5%为山地、丘陵，其中73%为喀斯特地形，喀斯特面积高达10.91万km2，占全省国土总面积的61.92%，土层浅薄且不连续，属于典型的生态脆弱区，同时也是世界上喀斯特地貌发育最为典型的地区之一。

喀斯特地区土壤富钙性特点明显影响和制约岩溶生态系统的运行机制[1]。喀斯特地区土壤中钙的分布特征对土壤中元素的沉积、溶解、理化指标以及水化学特征等都有重要影响，驱动并制约岩溶环境的元素迁移和生物有效性[2]。作为植物必须的营养元素，土壤中钙的含量直接影响植物的生长和发育[3]，与此同时，土壤中钙与有机碳的关系，直接影响到土壤生态系统平衡的维持，钙含量在不同岩石和土壤中的差异，导致钙在环境中分布的异质性[4]。由此可见，在土壤具有富钙性特点的喀斯特地区，对土壤中钙的空间分布特征开展研究具有重要的意义，有助于认清和了解土壤中钙的变化过程和区域化反应，同时能够加强对于土壤中钙迁移转化规律的科学认识，进一步揭示钙元素在喀斯特地区的生态与经济价值，可为喀斯特地区生态农业经济发展与生物多样性维持机制以及生态系统功能与稳定等相关研究提供一定的理论与基础数据积累。

1 材料与方法

1.1 数据采集与分析

于2019年10月在贵州省(荔波、施秉、红枫湖、安顺、平塘、惠水、花溪)采集表层土壤全钙数据，包括实际采集0～20 cm土层样品258个，案例推理样点100个，两类样点数据最终用于建模的样点共计290个，用于验证的样点共计68个(验证样点全部为实际采样数据)。采集土壤样品经自然风干、磨碎和过筛后备用，利用原子吸收分光光度计法测定土壤全钙含量，测定所参考标准为NY/T 296—1995《土壤全钙、镁、钠的测定》。

1.2 环境因子选取

选择气候、植被、地形以及岩性因子作为辅助表层土壤全钙预测的环境因子。预选的环境因子分别为年均气温、年均降水量、植被覆盖指数、地表粗糙度、坡度以及岩性钙值。气候数据来源于美国国家航空航天局网站(http://www.nasa.gov/)，植被数据来源于美国USGS(http://glovis.usgs.gov/)网站的Landsat8卫星数据，地形数据来源于中国地理空间数据云网站(http://www.gscloud.cn/)，岩性钙值数据来源于研究区1∶50万数字地质图和各类型岩性所对应的土壤全钙均值经ArcGIS软件处理后获取。

1.3 逐步线性回归

为避免由各环境因子之间的相关性引起多重共线性问题，从而导致模型模拟效果降低以及预测结果严重失真，故采用逐步线性回归方法选择最佳的环境因子。逐步回归分析的主要思路是在全部自变量中按其对因变量的贡献大小，由大到小地逐个引入回归方程，而对因变量贡献不显著的自变量不会被引入回归方程。

Y=β0+β1x1+β2x2+…+βixi+ε

(1)

式中，β0为常数；β(1，2，…，i)为自变量系数，ε为残差。

1.4 地理加权回归

地理加权回归(geographically weighted regression, GWR)模型由英国地理学家Fotheringham等提出，该模型利用自变量和因变量间的关系在不同空间上的变化进行非参数局部空间回归建模，模型中自变量的回归系数随空间位置而变化，对于空间数据具有较强的局部分析能力[5]，目前该方法在国内外已被多位学者应用，并取得了较好结果[6-10]，表达式为：

(2)

式中；(μi，vi)为第i个样点的地理位置，yi和xik是因变量y和自变量集xk在空间位置(μi，vi)处的实测值，β0(μi，vi)为在空间位置(μi，vi)处的常数项，βk(μi，vi)表示第i个样点的第k个回归系数，εi是第i个样点的随机误差。

1.5 数据验证

主要采用两种精度验证方法，一是利用实测样点值与预测样点值进行对比进度验证，利用线性拟合获取二者的相关性程度，以此表示模型预测的精度。二是利用在研究区内已有的相关研究，获取研究区内的平均值，再利用ArcGIS软件提取模型所预测的对应区域均值进行误差分析，以此表示模型预测的精度。

2 结果与分析

2.1 表层土壤全钙及环境因子的变异

从表1可知，研究区表层土壤全钙含量在0.81 ～33.99 g/ kg，平均值为11.03 g/ kg，变异系数为61%，土壤全钙含量整体水平较高，属中等变异强度，具有较高的空间异质性；坡度、岩性钙值以及植被覆盖指数也呈中等程度变异，其变异系数分别为77%、55%、21%；地表粗糙度、年均温度以及年均降水呈弱变异性，其变异系数分别为7%、8%、9%。

表1 表层土壤全钙及环境因子的描述性统计

2.2 模型估算辅助变量选择

从各环境因子与表层土壤全钙间的相关性(表2)可知，与全钙含量的相关系数为岩性钙值(0.33)>坡度(0.29)>植被覆盖指数(0.27)>地表粗糙度(0.26)>年均气温(0.21)>年均降水量(0.19)，其中岩性钙值与表层土壤全钙含量相关性最高，年均降水量和表层土壤全钙含量相关性最低。

表2 表层土壤全钙与环境因子的相关性

从表3可看出，模型2的效果要优于模型1(模型2的R2大于模型1)，故最终影响表层土壤全钙空间分布的主导环境因子为岩性钙值和坡度。

表3 逐步线性回归建模的决定系数

2.3 表层土壤全钙空间分布估算

基于GWR模型的贵州省表层土壤全钙空间分布估算模型如下：

(3)

式中，Ca为因变量，x为环境变量，β0(μi，vi)为常数项的回归系数，(μi，vi)xik为第i个样点上的第k个回归系数，是地理位置的函数，(Y)分别是指岩性钙值和坡度两个环境变量的回归系数，(S)为研究区岩性钙值的栅格图像，为研究区坡度的栅格图像，εi为随机误差项。

应用GWR估算的贵州省表层土壤全钙含量为0 ～23.44 g/kg(图1)，其空间分布特征主要表现为西南地区、东北地区以及西南向东北的过渡地区含量较高，而东南地区与西北地区普遍偏低。通过比较可发现低值区域所占的面积较小，且其表层土壤全钙含量较为接近，大多在0 ～8.61 g/ kg，说明在富钙性的喀斯特地区其表层土壤全钙含量整体水平较高。

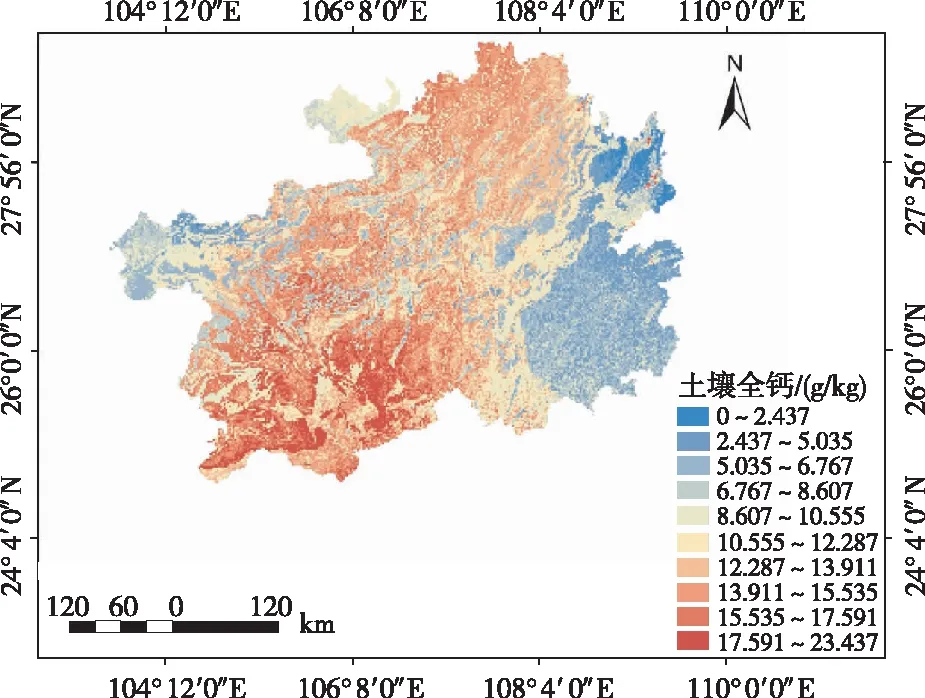
图1 基于GWR模型的表层土壤全钙空间分布

2.4 主导因子对表层土壤全钙空间分布的影响

通过两个主导环境因子的回归系数(岩性钙值回归系数0.05～1.09，坡度回归系数-0.08～0.36)可知(图2)，具有最大回归系数绝对值的环境因子是岩性，说明对研究区表层土壤全钙空间分布影响最重要的环境因子是岩性，其次为坡度，这与表层土壤全钙与环境因子的相关性分析结果一致。

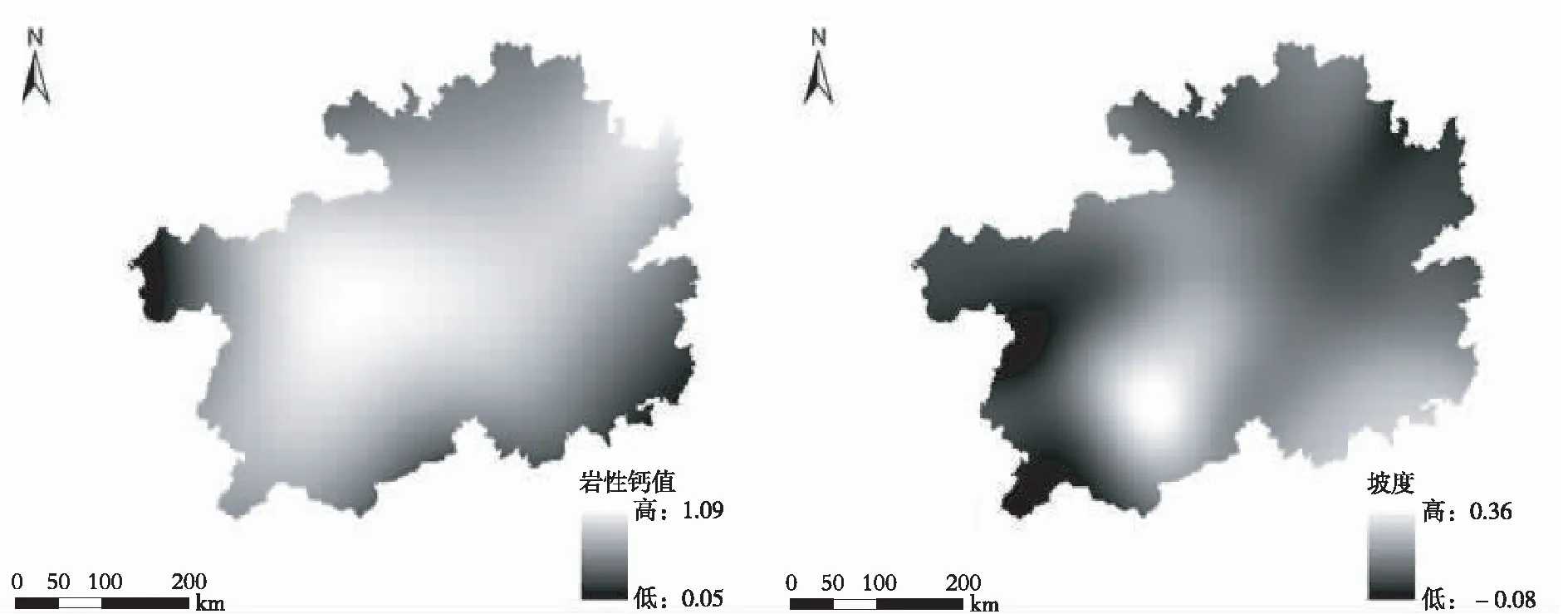
图2 表层土壤全钙解释变量回归系数的空间分布

回归系数的正负值，反映的是在多变量交互作用下自变量与土壤养分间的相关性方向，正的回归系数代表正的影响或相关，负的回归系数代表负的影响或相关。岩性因子对表层土壤全钙呈正的影响关系，且其影响程度从西南地区向东北地区递减，西北地区和东南地区影响程度最小。呈现该现象的原因可能是因为岩石作为土壤化学元素的主要来源[11]，基岩的类型会直接影响成土化学元素的组成，进而在一定程度上影响表层土壤化学元素的空间分布[12]。坡度因子对表层土壤全钙的影响从北部地区向南部地区递增，呈正的影响关系，但在西部地区和东部地区对土壤全钙呈负的影响关系。出现该现象的原因可能是因为坡度的大小会影响坡上水分以及土壤颗粒向坡下运移的速度和数量，从而影响土壤生物过程和化学过程，改变相应土壤性质[13]。从土壤侵蚀的角度上理解，即随着坡度的增大，土壤颗粒固有重力将更有利于溅散土粒向下坡运动，同时坡度的增大，降低了土壤的稳定性，土壤抗蚀能力减弱[14]，从而影响表层土壤全钙含量的空间分布。

2.5 表层土壤全钙空间分布估算模型精度验证

利用68个样点的实测值与其对应点位的预测值进行精度验证对比分析(图3a)可知，实测值与预测值二者呈现出较好的线性相关关系，相关系数R2为0.75，明显高于0.5，证明模型具有超过50%的预测精度。

区域精度验证分析(图3b)进一步表明，模型所预测的最大误差为29.2%，最小误差为6.6%，而平均误差仅为14.88%，因此，模型模拟的数据结果与实测数据结果具有较高的一致性，同时也进一步验证了模型模拟数据结果精度具有较好的可靠性。

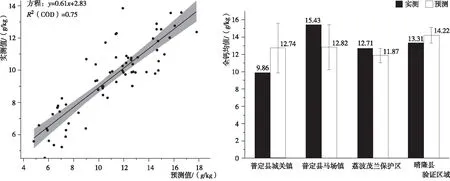
图3 土壤全钙实测值与预测值精度验证

3 结论与讨论

应用GWR对贵州省表层土壤全钙空间分布进行有效估算与分析，结果表明，1) 贵州省表层土壤全钙存在异质性且变异强度较大，影响其表层土壤全钙空间分布的主导因子为岩性和坡度，二者与表层土壤全钙呈显著正相关关系，表层土壤全钙空间分布异质性特征深受岩性和地形因子的影响。2) 贵州省表层土壤全钙含量为0 ～23.44 g/kg，表层土壤全钙含量整体水平较高，空间分布特征主要表现为西南地区、东北地区以及西南向东北的过渡地区含量较高，而东南地区与西北地区普遍偏低。3) 应用GWR模型估算贵州省表层土壤全钙空间分布整体结果较好，精度验证进一步表明模型具有较好的可靠性，模型估算精度优于传统的最小二乘回归。

应用GWR有效地对贵州省表层土壤全钙进行了空间分布的估算，估算结果具有较好的可靠性，但由于土壤养分制图精度受多种主客观因素的影响[15]，其制图精度有待进一步提高。首先，在样点的采集上，由于地理环境以及人力成本的原因，未能进行大面积的样点数据采集，使得模型估算精度可能受到一定影响，其次，在试验过程中也可能存在人为操作的误差使得模型估算精度受到影响，最后，选择的环境影响因子类型及数量可能也会影响模型估算的精度，因此，在接下来的进一步研究中，需进一步加大采样点的分布密度，并尽可能地控制好实验误差，筛选出更多对土壤钙元素有影响的环境因子作为协助变量进行建模，进一步提升模型估算的精度。