基于G-N迭代的双星时频差定位融合算法
2022-03-29徐英杰张文俊吴癸周郭福成
徐英杰, 张 敏, 张文俊, 吴癸周, 郭福成
(国防科技大学电子科学学院, 湖南长沙 410073)
0 引言
星载无源定位系统以其侦察范围广、不受天气气候影响、观测站是运动的等优点而受到国内外学者的广泛关注,目前已被普遍应用于军事和民用领域。星载无源定位技术中常用的观测量有到达时间差(Time Difference of Arrival,TDOA)、到达频率差(Frequency Difference of Arrival,FDOA)和到达角(Angle of Arrival,AOA)等,其中多星时差频差定位凭借其可瞬时定位及高定位精度的优势,在对雷达等脉冲辐射源的定位中应用更加广泛。
国内外的学者对多星时差频差定位算法进行了大量的研究,但以上研究仅针对单次定位进行改进且卫星使用数量多为三颗以上。文献[7]指出卫星定位系统在过顶期间会多次截获到地球上静止辐射源发出的信号,而有效利用多次截获的数据进行融合并定位可以提高定位精度并减少成本。
针对多次观测融合算法的研究,贾兴江等人针对双/多无人机测角频差系统提出了一种融合多次观测数据的定位算法,该算法在单次定位的基础上,引入了批处理加权最小二乘融合算法以及序贯加权最小二乘融合算法,实现了多次观测信息的有效融合。张莉等人提出了一种在观测站存在误差的情况下,运动双站对巡航目标的时差频差定位算法,该算法有效融合多次观测的数据并达到了克拉美罗下界(Cramer-Rao Lower Bound,CRLB)。文献[7]针对三星编队过顶期间对辐射源多次观测,提出了一种基于高斯-牛顿(Gauss-Newton,G-N)迭代的三星时差定位融合算法,该算法仅使用多次观测的时差信息和辐射源高程信息进行定位。实验证明该算法定位性能达到了CRLB且优于现有的位置合批处理方法。
本文将在时差定位的基础上融入频差信息,提出一种将多次观测的时差频差数据与高程信息融合的双星时差频差定位算法。具体思路为将不同时刻下观测到的时差信息和频差信息融合并结合辐射源高程信息构建代价方程,利用G-N迭代求解非线性最小二乘问题,迭代初值可以通过单次定位粗略得出,在使用相同数据的条件下,获得比现有位置合批处理方法更高的定位精度。
1 定位数学模型

将卫星1作为参考卫星,则双星在时刻下观测到的卫星2与1之间的TDOA定义为21,,即

(1)
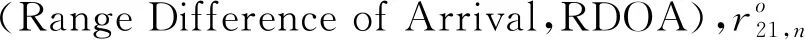

(2)
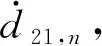
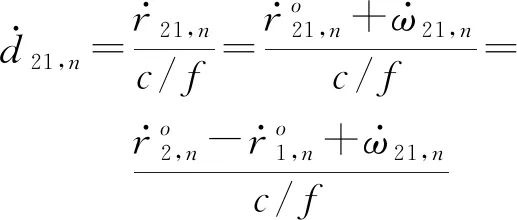
(3)
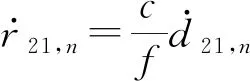
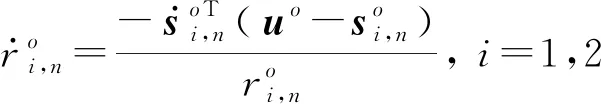
(4)
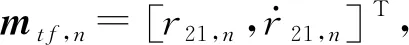
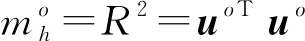
(5)
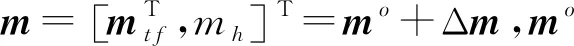
2 位置合批的融合算法
2.1 CRLB
由于考虑卫星存在误差的情况,因此未知参数=[T,T],令=[,],则
ln(;)=ln(;)+ln(;)=
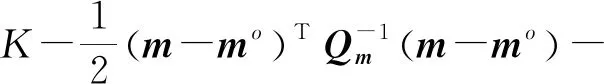
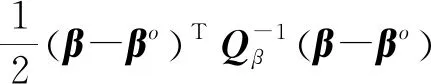
(6)
式中为常数。则未知参数的CRLB为

(7)
式中,
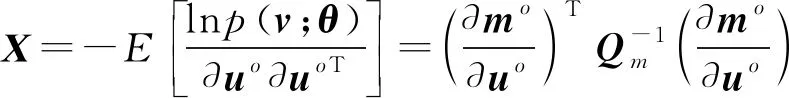

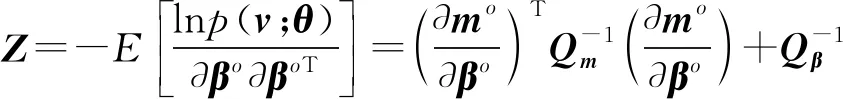
经计算可得辐射源的CRLB为
()=+
(-)
(8)
2.2 位置合批处理
工程上现有的位置合批处理方法主要有三种:一是取理论上的最优单次定位结果。假设在卫星过顶期间可以在个时刻截获到辐射源信号,则将时刻的单次双星时差频差定位理论误差设为(=1,2,…,),理论上的最优单次定位结果表示为

(9)
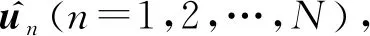

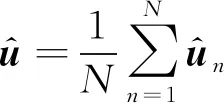
(10)

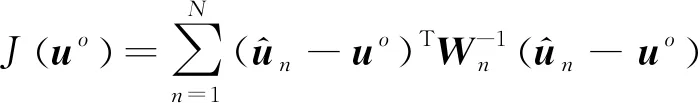
(11)
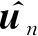
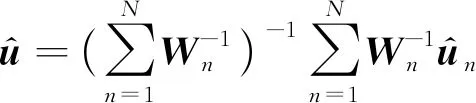
(12)
以上三种位置合批处理方法从理论上讲并不是最优的数据融合方法:理论上的最优单次定位结果仅使用了一次观测的数据;所有定位点的直接平均结果没有考虑卫星编队在不同位置下的定位精度是不同的;所有定位点的加权平均结果所使用的加权矩阵是单次定位所得。为此下文介绍了一种融合多次观测数据的理论最优定位算法。
2.3 基于G-N迭代的时差频差定位融合算法
本文算法参考文献[10]给出了一种仅需估计的加权最小二乘算法,其表达式如下:
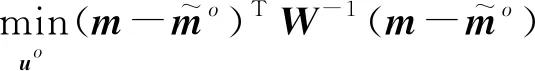
(13)


-1,,=1,…,,…,
(14)
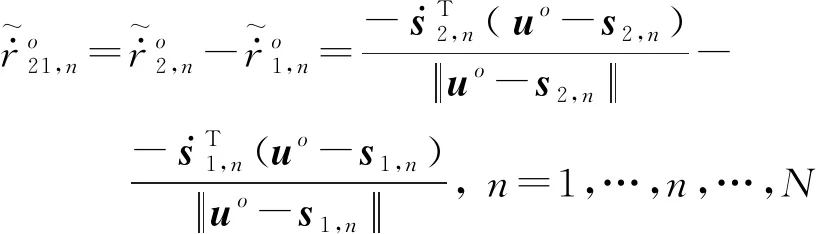
(15)
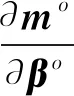
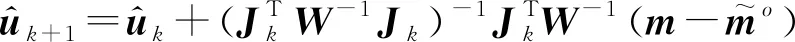
(16)
式中,为雅克比矩阵,

(17)
迭代初值可选取个观测时刻中的任一时刻得到的单次定位结果,其单次定位求解可参考文献[11]。通过球面迭代可将算法从正球面模型转换到WGS-84椭球模型来提高定位准确性。
3 仿真分析
本节通过实验验证上述算法。令辐射源位置的经纬度分别为1178° W和196° N,其高程为零。用于实验的卫星星历点数据基于STK软件生成,将同轨双星的轨道高度设为1 100 km,轨道倾角设为634°,星间距设为104 km,轨道历元时刻规定从2020年8月29日4时开始,卫星采样间隔设为1 s,整轨取960个星历点数据作为样本。
将时刻下观测的时差频差误差协方差阵,设为

(18)
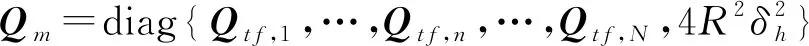
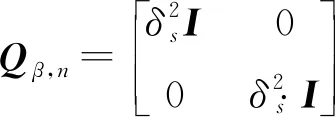
(19)

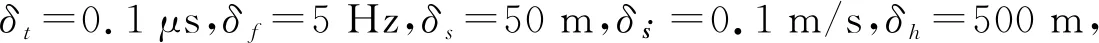
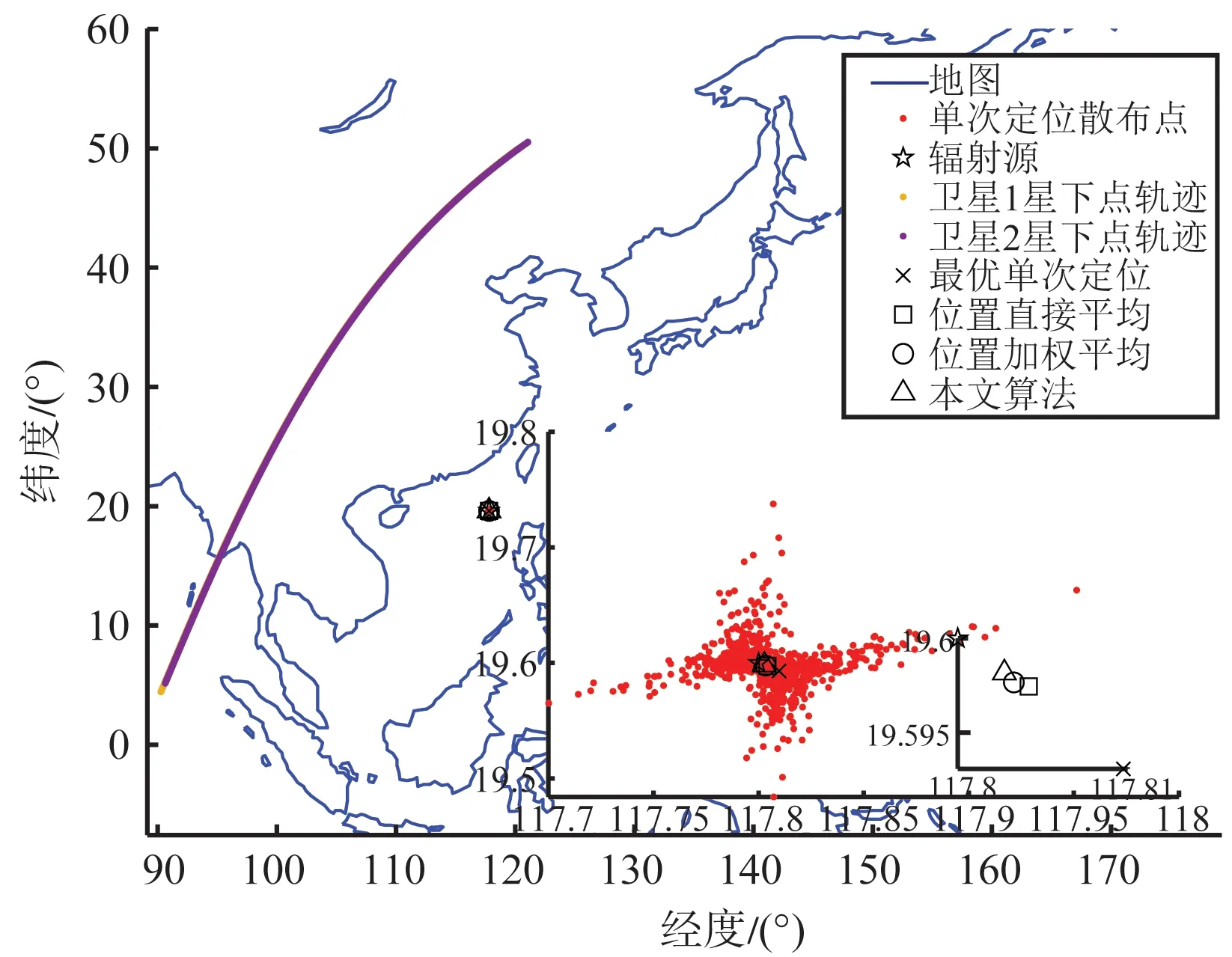
图1 卫星星下点轨迹和各种方法的定位点分布
通过计算位置估计的均方根误差(Root Mean Square Error,RMSE)来比较本文提出的算法和工程上常用的位置合批处理方法之间的性能,RMSE表达如下:
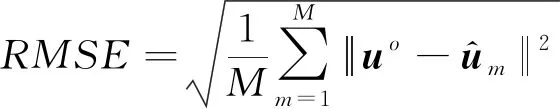
(20)
首先考虑理想情况下的电磁环境,这里的理想环境指卫星每秒都能截获到辐射源信号,测量误差和卫星误差依然存在。我们取融合次数分别取30,60,120,240,320,480和960次,即对得到的960个星历样本每间隔960s进行一次均匀采样,用采样所得星历点数据进行融合定位,比较不同融合次数下各种位置合批处理方法的定位精度,实验结果如图2所示。
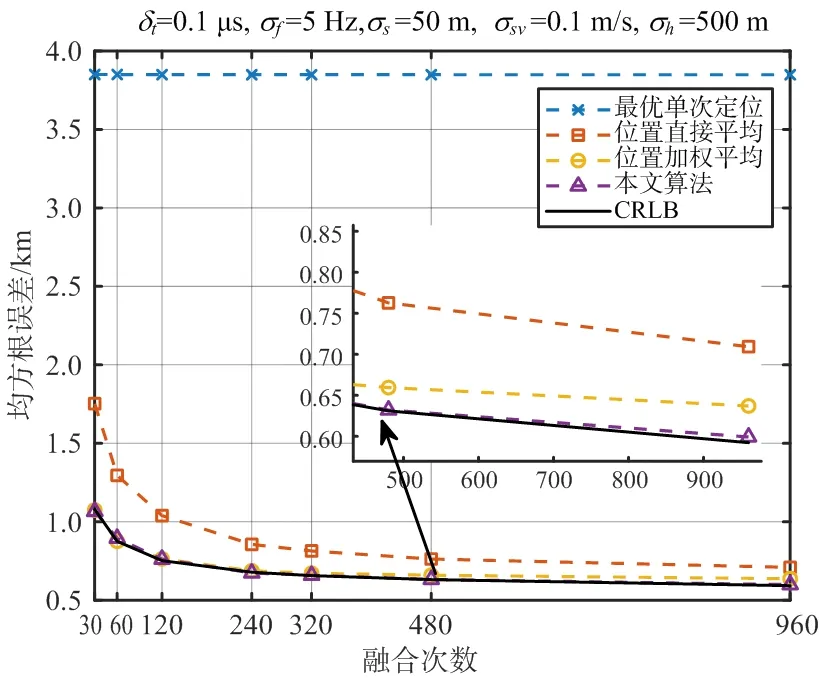
图2 理想电磁环境各种方法的定位精度对比
通过实验结果可以得出,在相同条件下,本文算法和位置加权平均都能达到CRLB,随着融合次数逐渐增多,本文算法的性能开始优于位置加权平均,而位置加权平均性能开始偏离CRLB;位置直接平均的性能要次于前两种方法,但是在融合次数较多的情况下要优于最优单次定位。
但是在实际工程应用中,空间电磁环境是复杂多变的,卫星过顶期间可能仅仅截获几次辐射源信号,因此这里取融合次数分别为2,3,4,5,6,8和10次,同样对得到的960个星历样本每间隔960/s进行一次均匀采样,用采样所得星历点数据进行融合定位,同样比较不同融合次数下各种位置合批方法的定位精度,实验结果如图3所示。
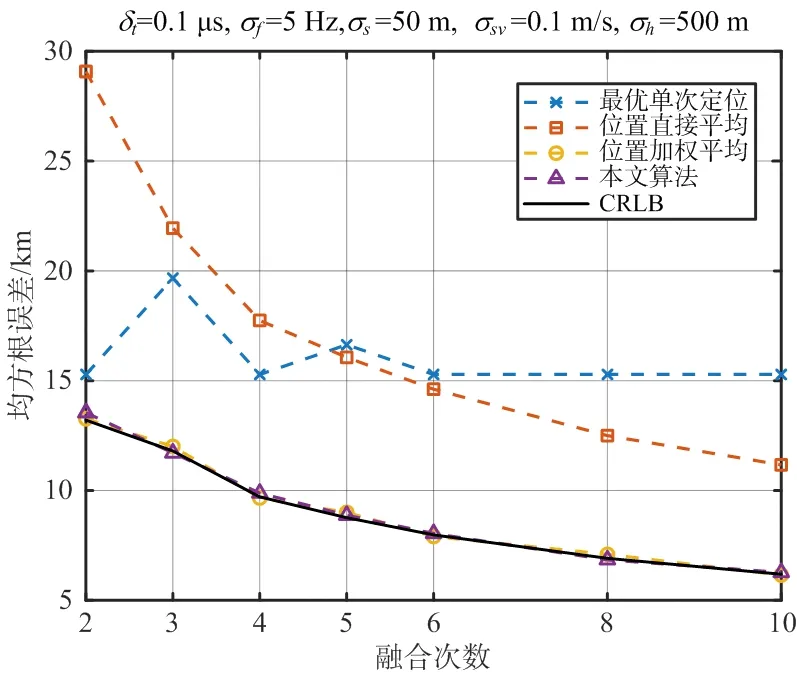
图3 复杂电磁环境各种方法的定位精度对比
通过实验结果可以得出,在相同条件下,本文算法和位置加权平均的性能都能达到CRLB且优于位置直接平均和最优单次定位;最优单次定位的性能一开始优于位置直接平均,当融合次数大于5次之后,位置直接平均的性能开始优于最优单次定位。
4 结束语
本文提出了一种基于G-N迭代的双星时差频差定位融合算法,有效地利用多次观测的时差频差和高程信息进行定位。通过实验验证,本文算法在理想电磁环境和复杂电磁环境下的定位精度要优于工程上现有的最优单次定位、位置直接平均和位置加权平均等位置合批处理方法。
