ARIMA模型和神经网络模型对我国GDP预测分析

李欣祎

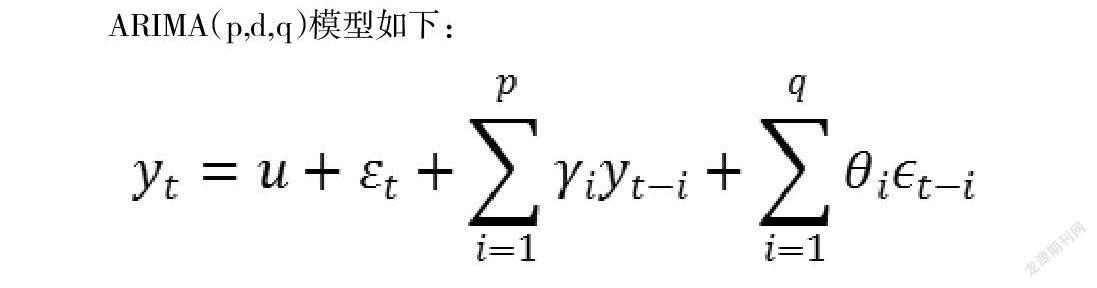
摘 要：国内生产总值（GDP）是衡量一个国家经济发展的重要指标，将宏观经济发展现状量化，研究近几十年来国家经济变动趋势和发展规律。本文主要借助ARIMA模型、BP神经网络两个模型，选取2000-2019年我国GDP季度数据进行拟合，分别将GDP季度数据划分为训练集和测试集，将两个模型拟合效果进行比较，研究发现，ARIMA模型的拟合效果较好。最后借助ARIMA对我国2020-2021年GDP进行预测。

关键词：ARIMA;BP神经网络;GDP

随着全球化进程的加快，我国综合国力得到大幅提升。经济快速发展的同时，暴露出一系列的弊端，贫富差距分化严重，社会矛盾问题凸显。此时，研究衡量我国经济发展的数据指标，对我国GDP的动态分析和预测对于及时调控国家的政策具有一定的重要意义。当前对GDP的研究主要借助时间序列模型，通过历史数据模拟未来数据变动趋势。此外还有借助机器学习算法等，模型操作简单，易于理解。近些年来，许多学者对GDP进行多方位研究，孙文渊（2015）借助1992-2011年吉林省GDP数据，通过比较传统回归模型主成分回归和机器学习模型神经网络拟合效果，研究发现，神经网络算法模型的预测效果要优于传统主成分回归模型;李超楠（2018）分别选取用ARIMA和BP神经网络两个模型进行分析，研究发现，两个模型组合的拟合效果最好，模型准确度较高，可以解决GDP数据中当期和滞后期的隐含的复杂关系。因此，本文选取时间序列ARIMA和神经网络两种方法对我国GDP进行分析预测。

一、理论基础

时间序列通过借助过去存在的历史数据对未来数据进行预测，研究数据指标的变化趋势。时间序列ARIMA模型是目前最常用的非平稳序列的时间序列模型。在日常生活中遇到的经济数据，大多都是非平稳数据，存在一定的趋势性和季节周期性，此时通过差分可以将数据平稳，防止出现数据的伪回归。

ARIMA（p，d，q）模型如下：

其中，p、q表示阶数，u是常数，ε代表误差。

一个完整的神经网络包括2个过程，首先是输入层输入数据，通过计算获得输出，如果输出层输出和正确数据不一致出现误差，且误差超出我们之前规定的误差，首先最后一层神经元参数调整，层层向第一层开始调整，直到输出结果误差达到最小。本文通过r语言进行实证分析。神经网络目前主要应用于经济预测，研究数据之间的非线性关系，操作简单。

二、实证分析

本文以我国2000-2019年每季度的GDP为研究对象，数据通过中经网统计数据集网站收集和整理得到。

（一）ARIMA模型

1.序列白噪声检验

在对序列进行分析前首先对序列进行白噪声检验，序列通过检验后才可以用时间序列分析，从结果来看，序列延迟6阶、12阶和18阶P都小于0.05，根据检验原理拒绝原假设，数据不属于纯随机波动，说明数据存在一定规律性可以用来分析。接下来利用SAS软件拟合模型。

2.数据的预处理

首先用SAS软件画出2000-2019年全国GDP时间序列图，发现2000-2008年GDP增长速度较为平缓，而从2009年以后每年增长速度迅猛。从总的趋势来看GDP增长呈现指数增长的趋势，说明这个序列具有非平稳性。由于序列具有指数趋势的序列特征，在时间序列中为了消除这种指数趋势通常把数据进行对数处理。把原序列进行对数处理后记为lnGDP。

经过对数处理后的序列呈线性增长，序列仍为非平稳序列lnGDP序列进行差分处理来转化成平稳序列。把2000-2016年的GDP数据作为训练样本，2017-2019年的GDP数据作为测试样本对模型测试结果进行评价。记序列lnGDP进行一阶差分后的序列记为dlnGDP画出时序图如图1所示。

从图1可以看出dlnGDP序列在某一值附近波动可以认为此时序列平稳。通过时序图判断具有一定主观性，为了更进一步检验序列平稳性，利用SAS软件对序列进行自相关偏自相关检验。经检验发现此时p值均小于0.01，表明此时dlnGDP序列是平稳序列。

3.模型建立

为了找到模型的最佳阶数，通过对自相关图和偏自相关图进行判断。序列经过一阶差分后达到平稳状态，然后分别做出序列dlnGDP的ACF图和PACF图。

从ACF图可以看出1阶之后全部没有超过标准差，且衰减程度慢可以判断自相关系数拖尾。从偏自相关图中能够看出，除了延迟1阶和7阶的偏自相关系数显著大于2倍标准差之外，其他偏自相关系數都比较小，所以考虑构建疏系数模型，综合考虑前面的差分运算，拟合疏系数模型ARIMA（（1，7），1，0）。使用条件最小二乘估计，确定模型为：

4.模型检验

模型显著性主要检验模型残差序列是否白噪声序列，可以得到误差序列延迟6、12、18和24阶都大于0.05不能拒绝原假设，认为残差序列属于白噪声序列即模型显著有效。

5.模型预测

把预测值和实际值进行对比表1：

2017-2019年每季度GDP的相对误差都在3%以内，三年的平均绝对百分比误差为0.90%，模型拟合效果较好，模型可作为全国GDP短期预测模型。

（三）BP神经网络

将所需的数据和相应的程序编写完成之后，运用R软件进行分析，得到相应的预测结果，由于神经网络的预测结果每次均不相同，所以取5次结果的平均值，如表2所示。

观察得到预测效果理想，BP神经网络预测值和实际值误差在10.5%以内，且预测误差均值为6.7%，但是由表中同样可以看出，随着时间增加，误差逐渐增大，BP神经网络模型可以很好的预测短期内的GDP，但是长期而言，误差逐渐增大。BP神经网络通过调整不同的参数，输出不同的拟合值，且同一个参数，多次重复也会输出不同的拟合值。因此，选取不同的参数对实验结果影响较大。

（四）ARIMA模型与BP神经网络模型拟合结果对比分析

为了更好的检验组合模型预测效果，分别计算ARIMA模型与BP神经网络模型拟合结果的相对误差百分比。比较ARIMA模型与BP神经网络模型两个模型的相对误差，可以发现ARIMA相对误差比BP神经网络模型相对误差小，并且在稳定性方面表现最好。

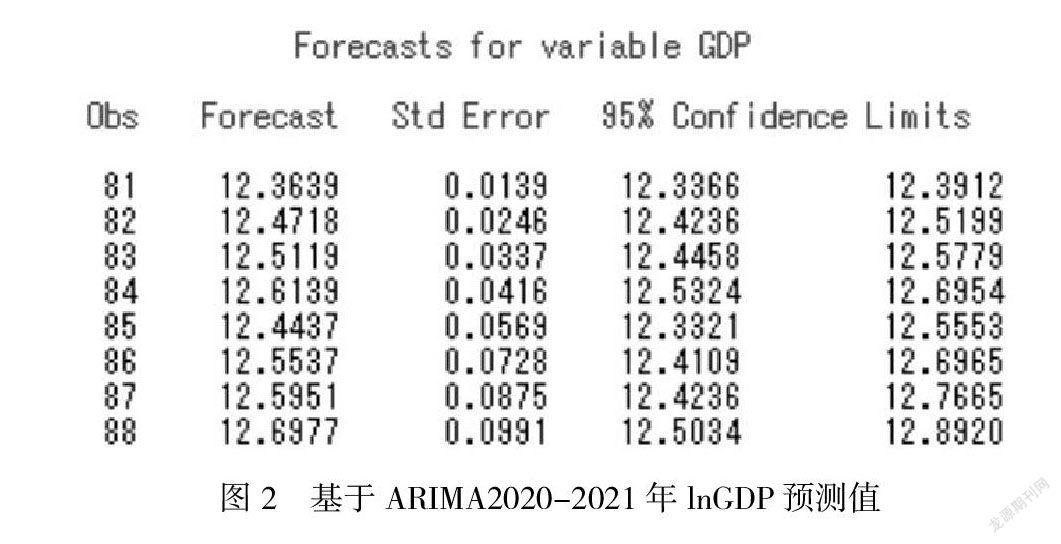
（五）预测

利用ARIMA模型对2020年-2021年8个季度的对数GDP进行预测。图为lnGDP预测值，红色线表示预测值，绿色中间部分表示95%的置信区间，具体lnGDP数值如图2，随着时间推移，预测结果波动范围逐渐扩大，误差逐渐增大。总体可以看出GDP呈现规律上升态势，但预测误差越来越大。

三、结论

ARIMA 模型和 BP 神经网络模型都可以用来预测GDP，并且被广泛使用，本文采用通过误差百分比方式来比较模型的预测精度。首先通过结合我国GDP数据特点首先基于传统的时间序列 ARIMA 模型对我国GDP进行拟合预测，提取当前期与滞后期的线性关系。根据自相关和偏自相关图结合疏系数选取最优的ARIMA（（1，7） ， 1 ， 0）模型来拟合2000年到2016年我国 GDP，根据该模型预测出2017年到2019年我国GDP数据，计算其平均绝对误差为0.90%。其次利用神经网络预测特点用 R 软件构建起 BP神经网络结构，结果ARIMA模型预测精度明显高于BP神经网络模型，说明ARIMA模型预测效果较好。借由最终选取的模型，对2020-2021年每季度GDP数值进行预测，并得到结果。

参考文献：

[1]孙文渊.基于BP神经网络模型下预测吉林省GDP[D].延边大学，2015

[2]李超楠.几种山东省 GDP 的预测方法及其比较[D].山东大学，2018

[3]蔡淅韵.基于ARIMA模型的国内生产总值预测[J].科技传播.2020（5上）： 40～41

[4]罗森，张孟璇.基于ARIMA和VAR模型的我国季度GDP预测比较[J].现代商业.2019（35）：50～52