基于灰色系统模型的用户借阅行为分析实证

卢成晓,陈添源

（闽南师范大学图书馆,福建 漳州 363000）

在互联网飞速发展的信息化时代，各类电子资源数量急剧增加，读者获取信息资源途径多样化，阅读方式多元化，传统的纸质馆藏资源已无法满足读者的个性化和精准化需求，各高校纸质图书借阅量呈下降趋势.分析流通数据及时准确地把握读者的阅读需求、阅读偏好和借阅行为规律，对优化纸质馆藏资源的采购计划，促进馆藏资源建设进而向读者高效提供精准化、个性化服务非常有指导意义.

1 文献综述

目前众多图书馆学者对高校图书馆流通数据进行了研究，主要有两大方面.一是对读者借阅行为数据方面的研究：如利用统计分析工具从读者借阅量、馆藏文献利用效率、借阅倾向等方面对流通数据进行统计分析[1-2]，得出馆藏资源利用率低、借阅量下降、文献利用率差异大等结论，并探究其原因，提出改进建议；探讨大数据技术如Apriori 关联规则算法、K-means 聚类算法、图书推荐算法等[3]在图书流通数据分析中的应用，以利于图书馆可以提高图书流通率及个性化服务水平，更好地服务于各种不同的用户；利用最小二乘支持向量机[4]极限学习机算法[5]、Logistic模型[6]等数据挖掘算法对读者借阅行为及影响因素进行分析；这些研究主要是采用定量定性分析相结合的方式从读者借阅行为数据的多个视角分析了高校图书馆馆藏资源利用现状、读者借阅特点等，进而探寻提高纸质图书利用率、提高读者服务水平的新思路.二是对借阅量预测方面的研究.目前有关借阅量的预测主要有利用ARIMA 时间序列理论[7]、灰色神经网络理论[8]、混沌时间序列理论[9]、线性回归理论[10]等，这些预测方法都需要大样本的数据进行分析.灰色预测模型因其“小数据”的建模特点被广泛应用于医学[11]、经济[12]、灾害预警[13]、人口[14]等许多方面.近年来已有学者将灰色预测模型应用到图书馆工作的探索中，如宋妍[15]、葛凡[16]、开滨[17]等采用GM(1,1)对图书馆文献借阅量和图书采购进行了预测分析.

为探索以用户需求为驱动的高校图书馆馆藏建设模式，更好地运用读者借阅行为数据洞察高校图书馆文献资料利用的变化趋势，从而有效驱动和精准提升图书馆的读者个性化、精准化的服务效能.本文尝试对某高校纸质图书借阅量进行时间序列分析，并选取经典GM(1,1)和改进的TDGM(1,1)对未来借阅量进行预测.

2 纸质图书借阅量分析

纸质图书借阅量是读者需求的客观反映，是衡量读者利用图书馆情况、图书馆文献资源利用率的重要依据之一.

2.1 数据来源

本文所用数据来源于金盘图书馆集成管理系统，借助系统的部分统计功能，获取2010—2017年纸质图书借阅量的月度数据、年度数据及分类图书借阅量的年度数据.

2.2 纸质图书借阅量变化趋势分析

2.2.1 月度借阅量分析

将2010—2017年纸质图书的月度借阅数据利用excel绘制成折线图如下图1.

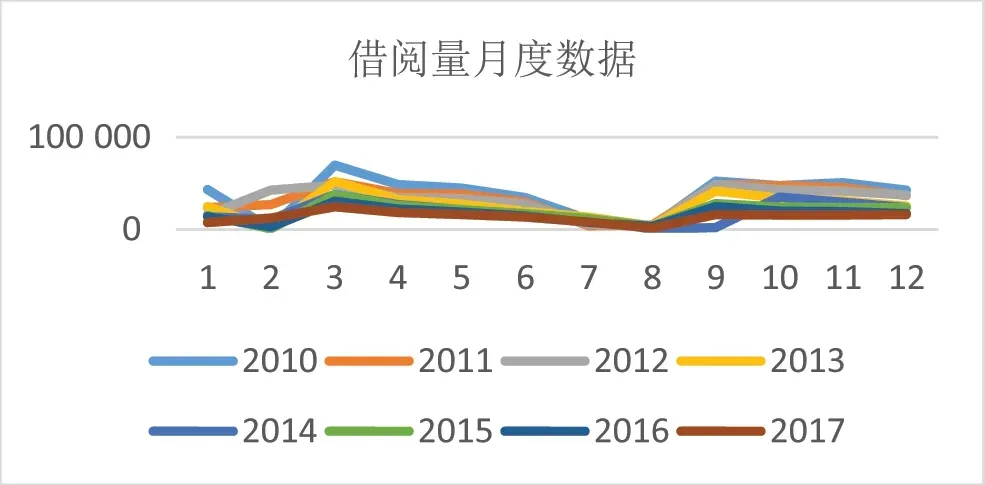
图1 2010—2017年月度借阅量变化趋势Fig.1 The tendency of monthly borrowing volume from 2010 to 2017

从图1可以直观看出，2010—2017年纸质图书借阅量的月度数据变化趋势基本一致并且呈现出明显的季节周期性，即每年的图书借阅旺季均出现在3、4、5、6、9、10、11、12 这八个月份，图书借阅的淡季均出现在1、2、7、8 这四个月份，其中3月份的借阅量最高，2、8月份的借阅量最低.此季节性的特点与实际情况相符，因为每年的2、8月份正值寒暑假故借阅量最低，3月份刚刚开学，新学期各项教学活动的正常运行，各类考试的备考及图书馆阅读推广活动的开展等使得借阅量达到最高.

2.2.2 年度借阅量分析

将2010—2017年纸质图书的年度借阅数据利用excel绘制成折线图如下图2.

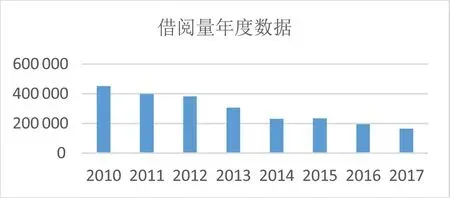
图2 2010—2017年年度借阅量变化趋势Fig.2 The tendency of annual borrowing volume from 2010 to 2017

从图2可以直观看出，2010—2017年借阅量的年度数据除2015年较2014年出现较小的增幅外，整体上呈明显的下降趋势并且下降幅度比较大.2017年的年度借阅量大概仅为2010年借阅量的三分之一.

2.3 读者借阅倾向偏好分析

2.3.1 读者借阅倾向分析

根据中图法分类，将2010—2017年各类纸质图书的年度借阅率利用excel绘制成折线图如下图3.

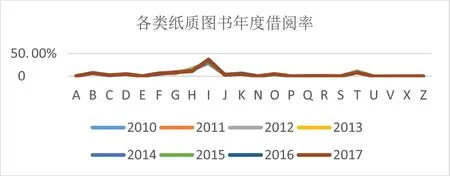
图3 2010—2017年各类纸质图书年度借阅率变化趋势Fig.3 The tendency of annual borrowing rate in various paper books from 2010 to 2017

从图3可以直观看出，2010—2017年各类纸质图书年度借阅率的变化趋势基本保持平稳，其中借阅量最高的是I文学类图书，其次为H 语言、文字类，T工业技术类，G 文科教体类、B哲学、宗教类图书；以上五类图书的借阅量占总借阅量的比率每年基本维持在70%左右；借阅量最低的为U 交通运输类、V 航空航天类图书.整体而言，社科类图书借阅量明显高于理科类图书借阅量.

2.3.2 读者借阅偏好分析

分析2010—2017年读者借阅的日数据，按照题名统计借阅次数并进行降序排列，得出2010—2017年各图书借阅次数及借阅排行前十的图书情况如下表1-2.

由表1可以看出2010—2017年年度借阅次数最高的图书其单本借阅次数整体呈现下降趋势；借阅次数少于10次的图书所占比例非常高并且呈逐年上升趋势，2017年高达97.6%，说明大部分图书的利用率非常低.

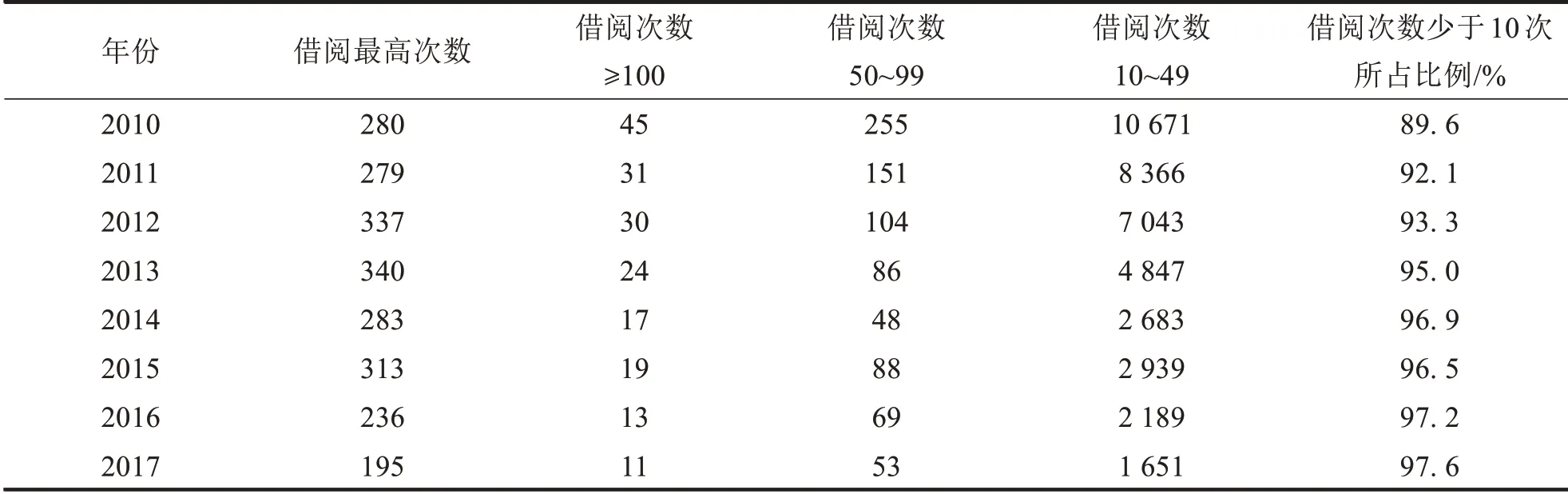
表1 2010—2017年各年图书借阅次数Tab.1 The borrowing times of books in each year from 2010 to 2017

由表2可以看出，2010—2017年间最受读者欢迎的书目大部分为文学类书籍，并且基本保持不变，其中《麦田里的守望者》《傲慢与偏见》《简·爱》三本书是读者的最爱.

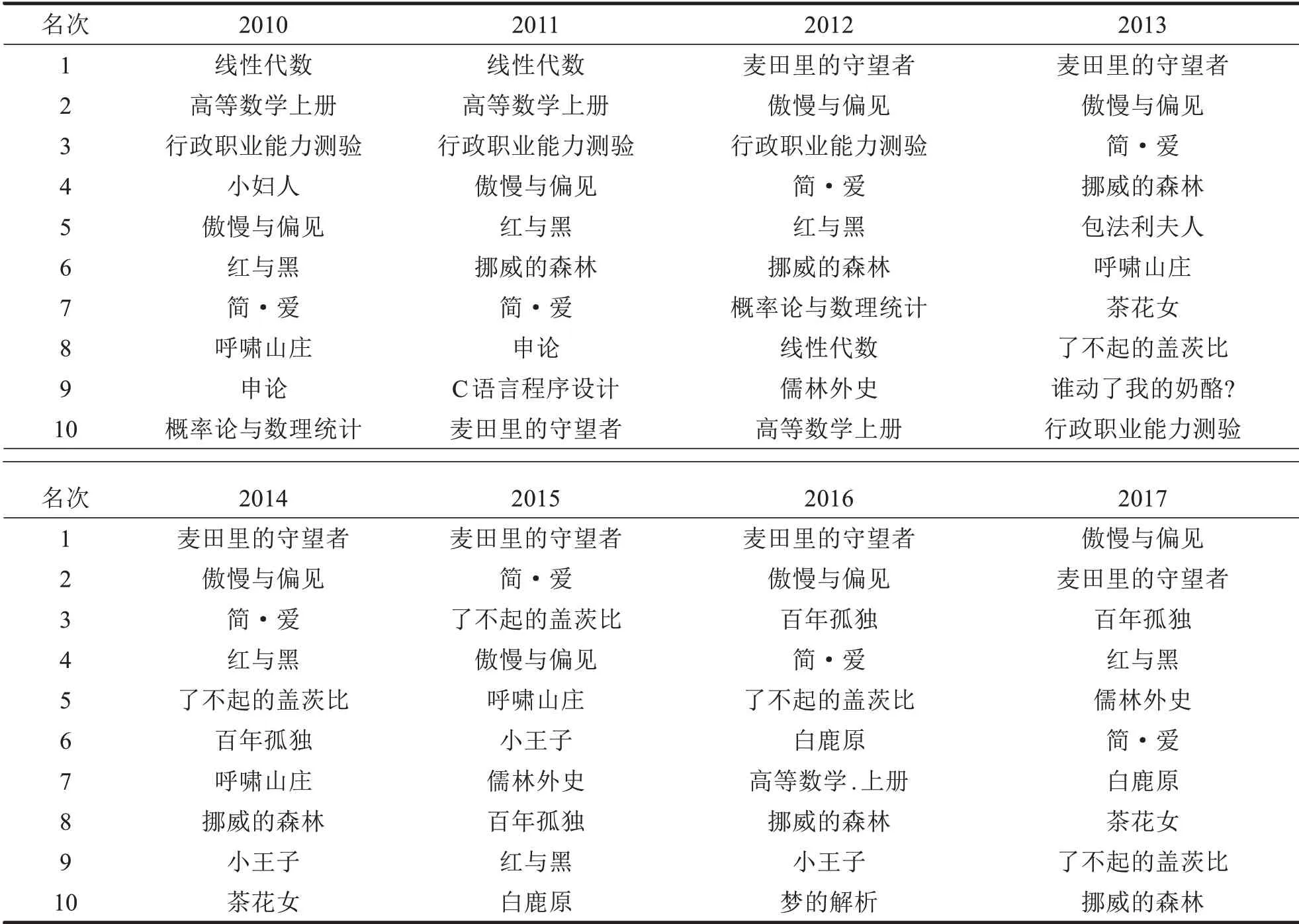
表2 2010—2017年图书借阅排行前十名书目Tab.2 Top 10 books for borrowing from 2010 to 2017

3 纸质图书借阅量模型分析

本文选用经典GM(1,1)和改进的TDGM(1,1)(three parameter discrete gray model)对2010—2019年纸质图书年度借阅量进行模拟及预测，其中2010—2017年的数据用于建模，2018—2019年的数据用于验证模型的预测性能，最后利用所选模型预测2020—2023年的借阅量.

3.1 模型介绍[18]

定义设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，其x(0)(k)≥0,k=1,2,…,n；X(1)为X(0)的一次累加生成序列，即X(1)=(x(1)(1),x(1)(2),…,x(1)(n))，其中k=1,2,…,n；Z(1)为X(1)的紧邻均值生成序列，即Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))，其中z(1)(k)=,k=2,3,…,n.

3.1.1 GM(1,1)

GM(1,1)的基本形式：x(0)(k)+az(1)(k)=b，其中a、b为待估参数.进一步定义

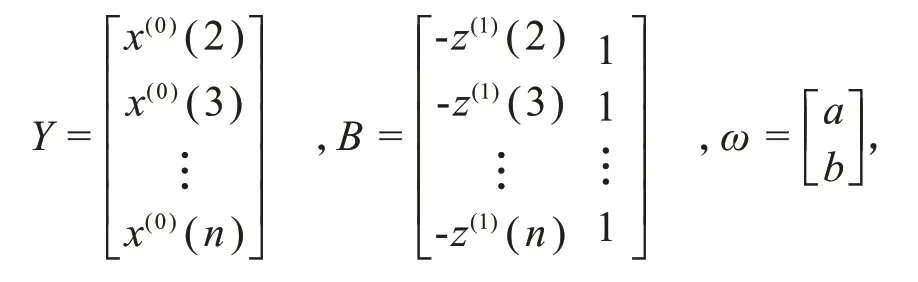
利用最小二乘估计法可求得

将其带入GM(1,1)的白化方程

可得到该模型的时间响应式为：

进一步简化得到GM(1,1)的最终还原式为：

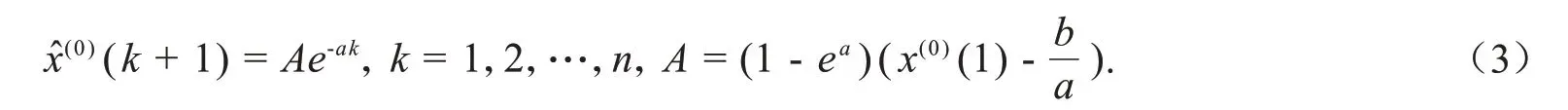
故称GM(1,1)为齐次指数序列灰色预测模型.

3.1.2 TDGM(1,1)

TDGM(1,1)为三参数离散灰色预测模型，其基本形式为：x(0)(k)+a1z(1)(k)=kb1+c1，其中a1、b1、c1为待估参数.

进一步构造矩阵

利用最小二乘估计法求得

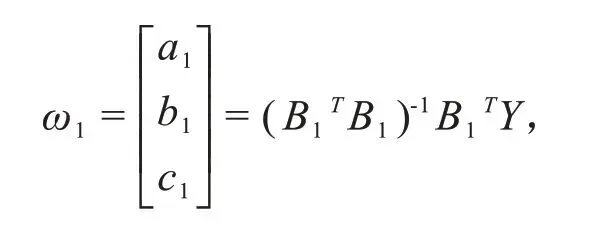
进一步计算得到该模型的时间响应函数的简化式为

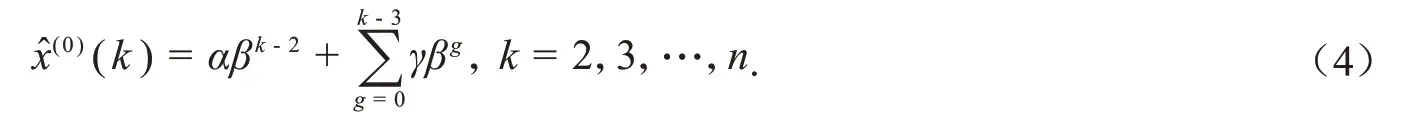
其中，α=

说明：公式（3）和公式（4）中，当k=2,3,…,n时,(k)称为模拟值；当k=n+1,n+2,…时,(k)称为预测值.

3.2 模型建立及比较

3.2.1 数据处理

统计2010—2017年的纸质图书总借阅量数据如下表3所示.

表3 2010—2017年的纸质图书总借阅量Tab.3 The total borrowing volume of paper books from 2010 to 2017

分别将2010—2017年对应k的取值为1 到8，由表3得到原始序列X(0)并根据上述定义计算得到其一次累加序列X(1)、紧邻均值生成序列Z(1)，数据汇总如下表4所示.

表4 原始序列、一次累加序列、紧邻均值生成序列数据Tab.4 The data of original sequence,one-time accumulation sequence and nearest neighbor mean generation sequence

3.2.2 计算GM(1,1)的时间响应函数

将表4中的相关数据代入上述GM(1,1)的构造矩阵得到如下具体矩阵：

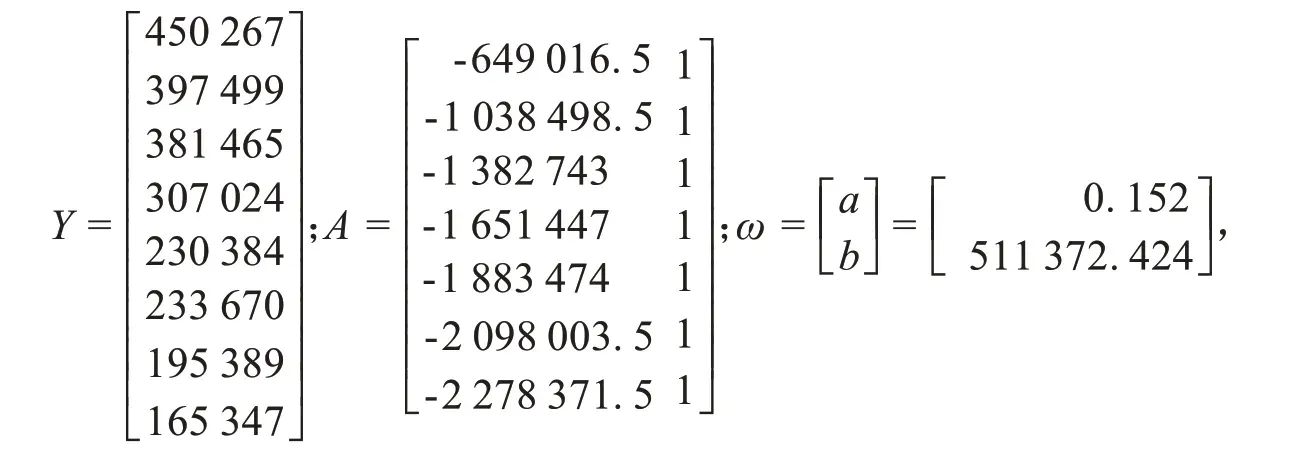
代入上述公式（1）得到如下具体表达式

代入上述公式（3）得到GM(1,1)的最终时间响应函数如下：

3.2.3 计算TDGM(1,1)的时间响应函数

将表4中的相关数据代入上述TDGM(1,1)的构造矩阵得到如下具体矩阵：

代入上述公式（4）得到TDGM(1,1)模型的时间响应函数表达式如下：

3.2.4 模拟及预测数据对比分析

令(1)=x(0)(1)利用公式（6）和（7）分别计算k=2,3,…,8 时,GM(1,1)和TDGM(1,1)的模拟值和模拟误差；k=9,10时，GM(1,1)和TDGM(1,1)的预测值和预测误差.结果汇总如下表5-6所示：

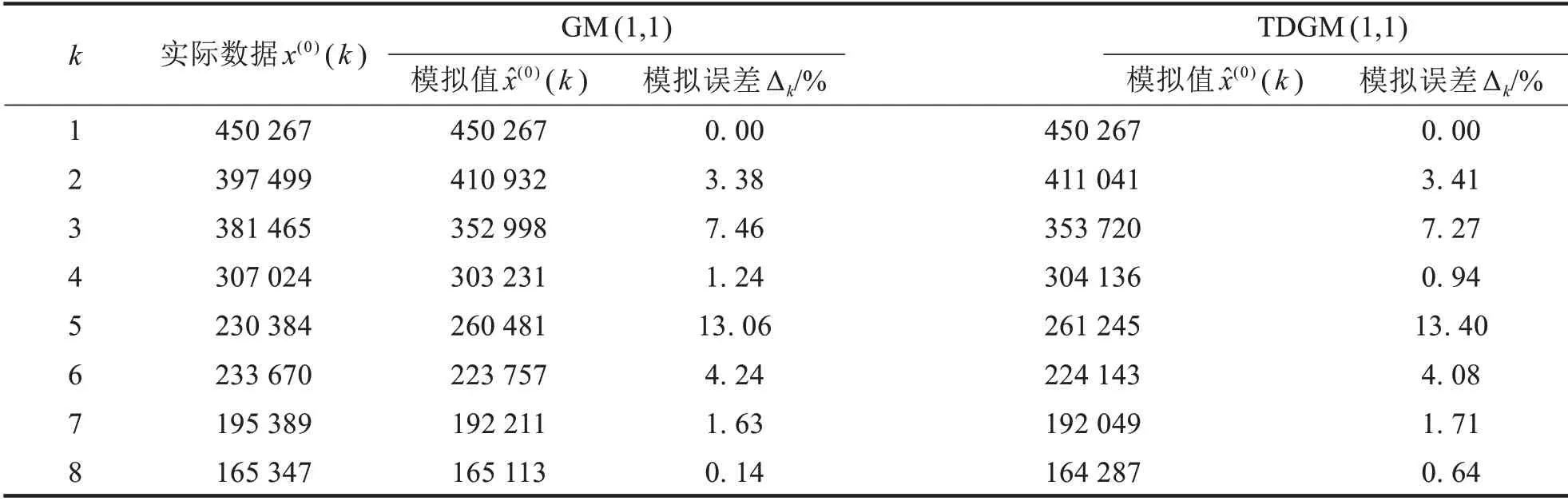
表5 GM(1,1)和TDGM(1,1)模拟结果对比Tab.5 The comparison of GM(1,1)and TDGM(1,1)in simulation results

其中，ε(k)=

据表5数据计算出GM(1,1)和TDGM(1,1)的平均相对模拟误差分别为3.89%和3.93%，发现其基本相同且均小于0.1，说明模型拟合效果比较好.

据表6数据计算出GM(1,1)和TDGM(1,1)的平均相对预测误差分别为4.44%和2.87%，发现TDGM(1,1)的平均相对预测误差明显低于GM(1,1)的值.

表6 GM(1,1)和TDGM(1,1)预测结果对比Tab.6 The comparison of GM(1,1)and TDGM(1,1)in prediction results

综合上述结果，选用TDGM(1,1)预测未来四年的纸质图书借阅量更优.

3.3 模型检验

本文采用后验差方法检验上述两个模型的模拟性能.

3.3.1 后验差方法检验步骤[16]

（1）首先计算原始序列X(0)和模型残差序列ε的均方差，分别记为S1,S2，具体计算公式如下：

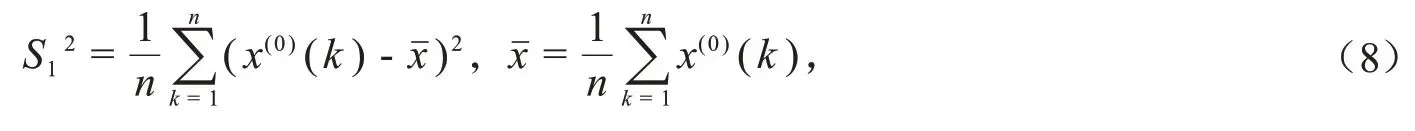
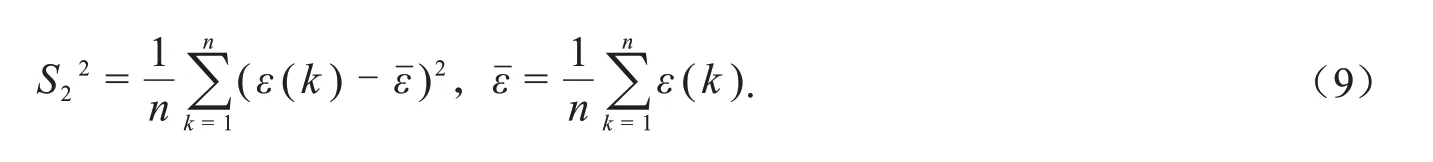
（2）计算后验比值：

（3）评定预测模型的精度等级.

一般当C< 0.35 时，模型精度I 级好；0.35≤C< 0.5 时模型精度II 级合格；0.5≤C< 0.65 时，模型精度III级一般；当C≥0.65时，模型精度IV级不合格.模型精度为I级和II级是合格模型，可用于预测.

3.3.2 GM (1,1)和TDGM(1,1)预测精度等级

将上述GM(1,1)和TDGM(1,1)的相关数据代入公式（8）和公式（9）计算两个模型的后验比值结果如下：

GM(1,1)的后验差比值记为CG：

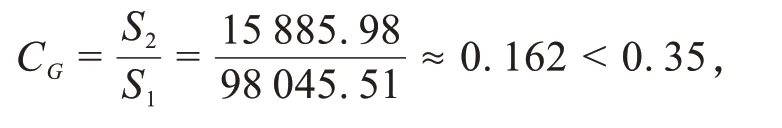
评价等级I级（好）.

TDGM(1,1)的后验差比值记为CT：

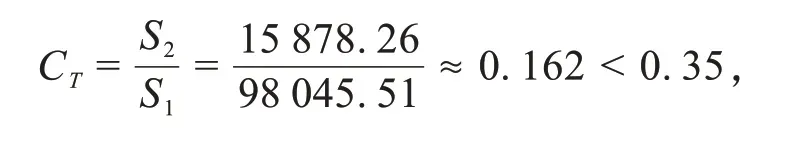
评价等级I级（好）.

对比精度检验等级，GM(1,1)和TDGM(1,1)预测模型都属于合格模型，都可以用来预测.

3.4 模型预测

综合上述分析，我们最终选择TDGM(1,1)对2020—2023年的纸质图书借阅量进行预测，预测结果如下表7所示.

表7 2020—2023年纸质图书借阅量预测Tab.7 The prediction of borrowing volume of paper books from 2010 to 2023

预测结果显示纸质图书借阅量持续呈下降趋势，而且下降的幅度逐年增加，2023年借阅量的预测值仅为2010 的13.5%.经查询2020年和2021年纸质图书借阅量的真实数据分别为44 559 册和79 658 册。受疫情影响，2020年学生在校时间比往年少，故2020年借阅量的预测值与真实值相差非常大；2021年的预测误差为7.95%，说明上述模型的预测精度比较高.

4 结语

本文对2010—2017年的纸质图书借阅量进行了分析，结果显示纸质图书借阅量的月度数据变化趋势基本一致并且具有明显的季节周期性；年度借阅量呈明显的下降趋势并且下降速度比较快；2010—2017年各类图书的年度借阅率的变化趋势基本保持平稳，借阅量位居前五的I、H、T、G、B五类图书的借阅量占总借阅量的比率每年基本维持在70%左右，整体而言，社科类图书借阅量明显高于理科类图书借阅量.最终选取的TDGM(1,1)预测模型结果显示纸质图书借阅量持续呈下降趋势，而且下降的幅度逐年增加，2023年借阅量的预测值仅为2010的13.5%，该模型的预测精度比较高.

针对上述纸质图书借阅量的变化趋势及特点，高校图书馆阅读推广小组应该充分利用新生入馆教育、新书推荐宣传及展示、阅读排行榜推荐、举办阅读比赛活动等方式，吸引读者的阅读兴趣，让读者变被动阅读为主动阅读；加强馆员数据挖掘技术的培训，通过定期对流通数据的详细分析，及时掌握读者的借阅规律、借阅倾向；结合读者荐购方式，优化新书采购计划，促使图书馆选购的图书能吸引读者的阅读兴趣，满足读者的阅读需求，进而提高纸质图书的利用率.