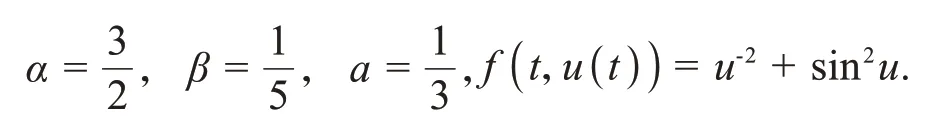含两项分数阶导数的边值问题正解的存在性
2022-03-28许勇强
罗 茜,许勇强
(闽南师范大学数学与统计学院,福建 漳州 363000)
研究了以下零边值条件的分数阶微分方程,即

其中:和分别是阶数为α,β的Caputo 型分数阶导数,1<α≤2,0<β≤1,a为给定的正数,函数f:[0,1]×(0,∞)→[0,∞)连续.
分数阶微分方程因在物理、力学、化学、工程、金融、混沌、粘弹性等领域得到广泛应用而备受关注,详见文献[1-13],这里考虑的大多都是一个分数阶导数的情况.但是,对于一般的多项分数阶微分算子的微分方程似乎没有太多结果.1984年,Bagley等[14]公式化牛顿流体中薄板运动的数学模型为
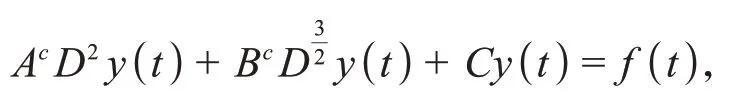
后被称为Bagley-Torvik方程.这里A,B,C都为常数,f是给定的函数.在Fazli等[15]通过不动点定理研究当边值问题中导数的阶数α=2 且函数f满足某些特定条件时正解的存在性.Ibrahim,Dong 等[16]用同样的方法证明了方程边值问题解的存在唯一性.Hao等[17]考虑了下列四阶m点边值问题为
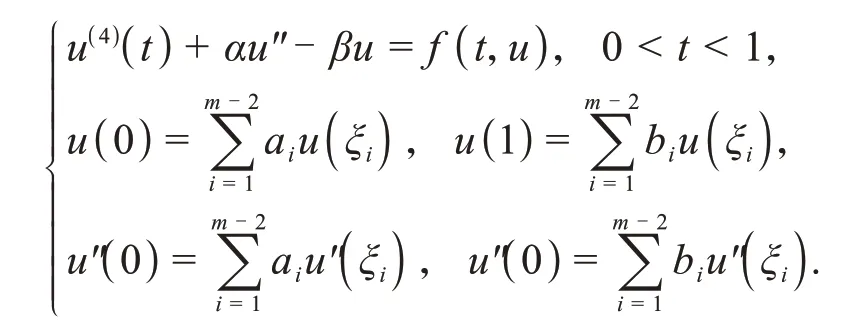
通过不动点理论得到了两种情况下正解的存在性,
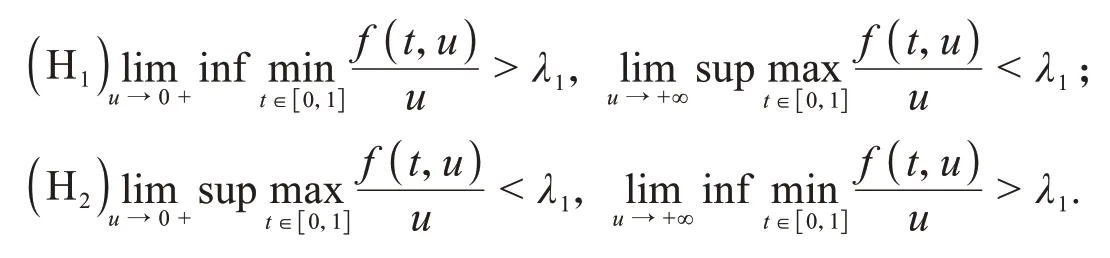
其中:λ1是相关线性算子的第一特征值.
受上面启发,本文的目的是在类似于(H1)和(H2)的条件下采用不动点指数理论和Guo-Krasnoselskii不动点定理方法[17-23]研究边值问题(1)正解的存在性.与现有文献相比,本文讨论的是含两项分数阶导数的微分方程.其次,非线性项f(t,u)满足与相关线性算子的第一特征值有关.最后,分析了相关线性算子的谱和格林函数的性质.
1 预备知识
定义1[24]Caputo意义下函数f:(0,∞)→R的α阶导数是指
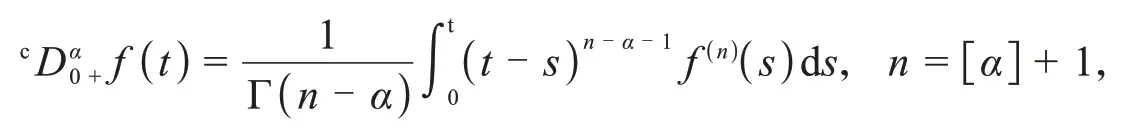
其中[α]是实数α的整数部分,右端在(0,∞)上是逐点定义的.
定义2[25]设f(t)和g(t)都满足当t< 0 时f(t)=g(t)=0,则称和g(t)的卷积,记为f(t)∗g(t)=g(t)∗f(t)=
引理1对于边值问题

给定函数f∈C([0,1],R),那么边值问题式(2)解的表达式u∈C([0,1],R)可以写为
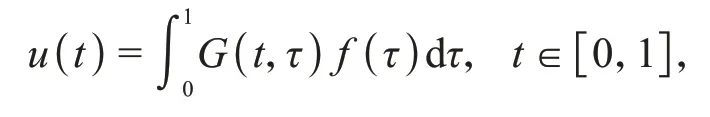
其中
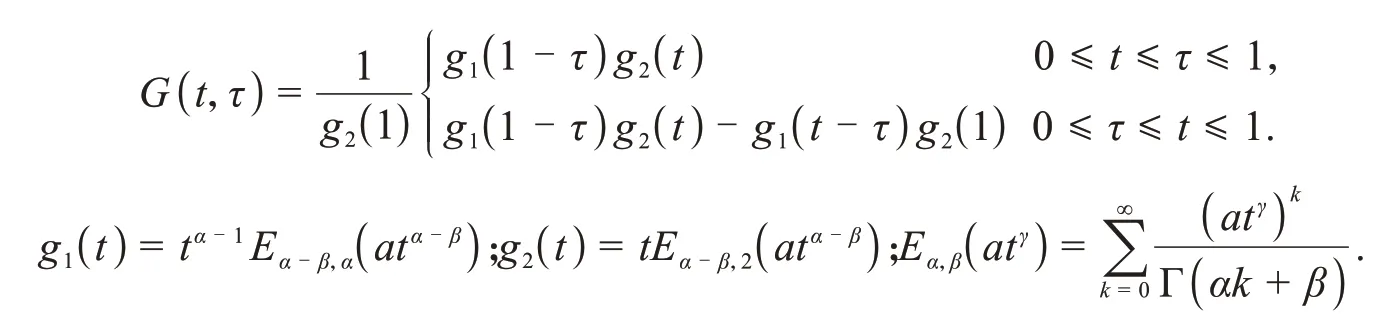
证明对-cDα0+u(t)+acDβ0+u(t)=f(t)应用拉普拉斯变换,可得
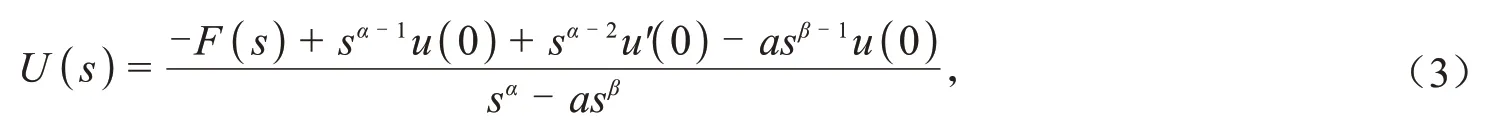
对式(3)两端应用拉普拉斯逆变换,有
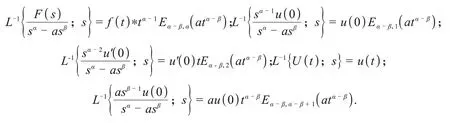
从而
u(t)=-f(t)∗tα-1Eα-β,α(atα-β)+u(0)Eα-β,1(tα-β)+
u′(0)tEα-β,2(atα-β)-au(0)tα-βEα-β,α-β+1(atα-β).
其中,等式右端第一部分可根据定义2得
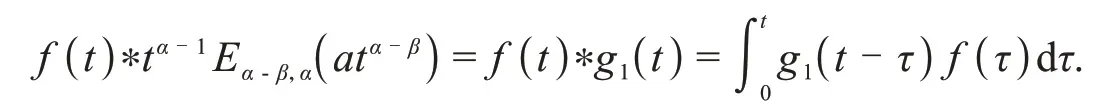
再利用边值条件u(0)=0,u(1)=0,直接计算可解得u′(0)=于是

显然,G(t,τ)在[0,1]×[0,1]上为连续函数.
引理2格林函数G(t,τ)满足以下性质:
1)G(t,τ)>0 ∀t,τ∈(0,1);
2)G(t,τ)≥
3)G(t,τ)≤(1-τ)α-1tg1(1)∀t,τ∈[0,1].
证明)1 性质1可由性质2得.
2)对任意t∈[0,1],显然有
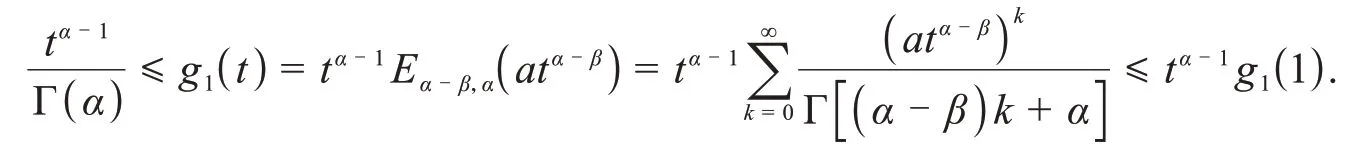
类似地,
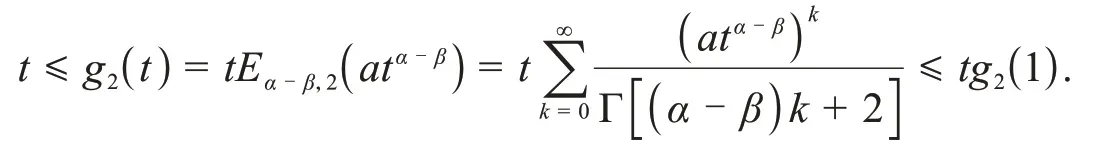
当0≤t≤τ≤1时,
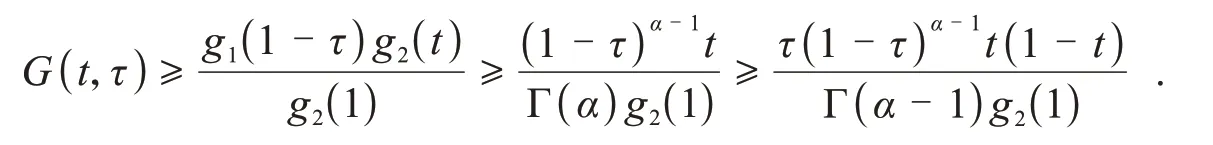
当0≤τ≤t≤1时,
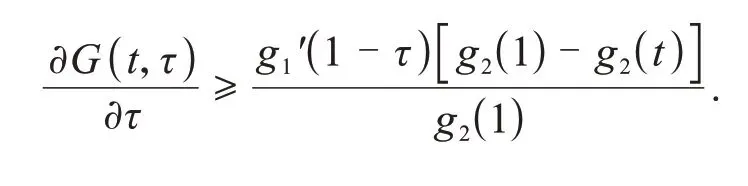
利用Lagrange中值定理,∃ξ∈(1-τ,1),η∈(t,1)使得
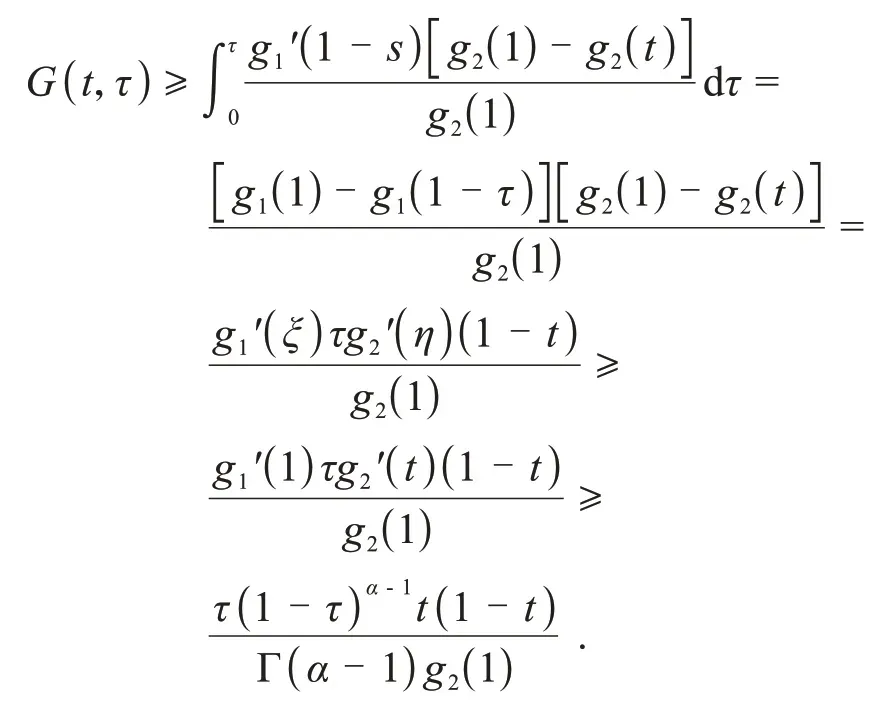
因此,性质2成立.
3)当0≤t≤τ≤1时,
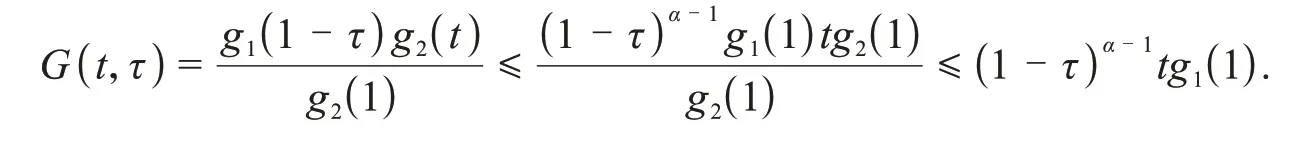
当0≤τ≤t≤1时,

容易证得性质3成立.
定义算子T和L,
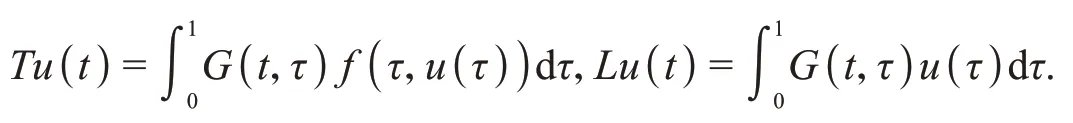
为了方便,列出一些之后会用到的假设条件:
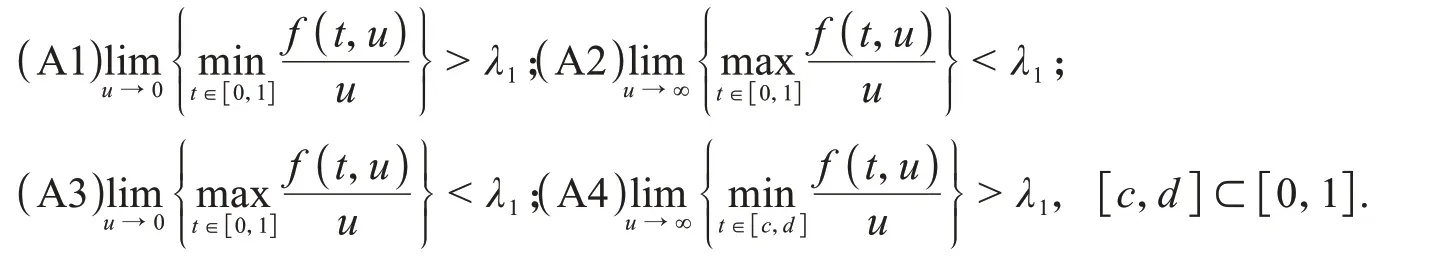
其中,λ1是算子L的第一特征值.
K={u∈E:u(t)≥0,t∈[0,1]},
显然K是E中的锥.
引理3对于任意r>0,T:K→K完全连续.
证明由G(t,τ)和f(t,u(t))的连续性可知T连续.设Q⊂K是有界的,则对任意u∈K,存在ρ>0 使得‖u‖≤ρ.另外,f在[0,1]×[-ρ,ρ]上一致连续,则存在M>0,使得f(t,u(t)) 即T(Q)是一致有界的. 接下来,证明T为等度连续算子.任意u∈Q,t1,t2∈[0,1]且t1 即 那么,T是等度连续的.根据Arzela’-Ascoli定理,T:K→K是完全连续的. 引理4[21]K为Banach 空间E中的锥,设L:E→E是完全连续线性算子,L(K)⊂K.如果存在ψ∈E(-K),ψ∉-K,常数c>0,使得cLψ>ψ,则谱半径r(L)≠0并且有L的正特征函数φ1对应的第一特征值λ1=(r(L))-1,使得λ1Lφ1=φ1. 引理5若是谱半径r(L)≠0且有L的正特征函数φ1对应的第一特征值λ1=(r(L))-1则λ1Lφ1=φ1. 证明通过常规方法可证算子L是完全连续线性算子.对任意u∈K,u(t)≥0,有 那么,(Lu)(t)∈K这表明L(K)⊂K.根据引理2 知,存在[a,b]⊂[0,1]使得对任意t,τ∈[a,b]都有G(t,τ)>0.令ψ∈C[0,1],则对∀t∈[a,b]都有ψ≥0,而对∀t∉[a,b]有ψ=0.当t∈[a,b]时,有 因此,存在常数c>0使得cLψ≥ψ,根据引理4结论成立. 引理6[22]K为Banach 空间E中的锥,Ω为E中有界开集.假设T:∩K→K为完全连续算子.若存在u0∈K-{θ}使得 u-Tu≠λu0,∀λ≥0,u∈∂Ω∩K, 那么,i(T,Ω∩K,K)=0. 引理7[22]K为Banach空间E中的锥,Ω为E中有界开集.假设T:∩K→K为完全连续算子.如果 Tu≠λu,∀λ≥1,u∈∂Ω∩K, 那么,i(T,Ω∩K,K)=1. 引理8[26]设E是Banach 空间,K是E中的锥.假设Ω1,Ω2是E中的有界开集,θ∈Ω1,⊂Ω2,令T:K∩(1)→K是全连续算子,并且使得下列条件之一成立: 1)‖Tu‖≤u,u∈K∩∂Ω1且‖Tu‖≥u,u∈K∩∂Ω2, 2)‖Tu‖≥u,u∈K∩∂Ω1且‖Tu‖≤u,u∈K∩∂Ω2, 则算子T在K∩(1)中至少有一个不动点. 定义邻域Br={u∈E:u 定理1假设(A1)和(A2)成立,那么边值问题式(1)至少有一个不动点. 证明根据假设(A1)知,存在r1>0使得f(t,u)≥λ1u,∀[t,u]∈[0,1]×[0,r1].那么 反证法,假设算子T在∂Br1∩K中有不动点,则 否则,存在μ0>0 和u1∈∂Br1∩K,μ>0,使得u1-Tu1=μ0φ1,即u1=Tu1+μ0φ1≥μ0φ1.令=sup{μ|u1≥μφ1},则≥μ0且μ1≥μφ1.由L为单调递增的线性算子可知 由条件(A2)知,存在r2>r1,0<δ<λ1,令使得 定义算子L1,令L1u(t)=(λ1-δ)Lu(t).显然,L1:E→E为有界线性算子.设 H={u∈K|μu=Au,μ≥1}. 接下来,要证H有界.对∀u∈H都有 其中G=G(t,τ),因此(I-L1)u(t)=GF,t∈[0,1].由引理4知r(L)=故r(L1)=r((λ1-故(I-L1)-1存在.那么u(t)≤(I-L1)-1GF,t∈[0,1].因此,H有界.取R>应用引理7可得 结合式(6)和式(9)可得 则T在∩K中至少有一个不动点,即边值问题(1)至少存在一个正解. 定理2假设(A3)和(A4)成立,则边值问题式(1)至少有一个正解. 证明令≤1,根据(A3)可知存在0 f(t,u)≤λ1u,∀[t,u]∈[0,1]×[0,r3]. 定义一个E中的开集Ω1,Ω1={u(t)∈E:‖u‖ 因此‖Tu(t)‖≤‖u‖,∀u∈∂Ω1∩K. 定义一个E中的开集Ω2,Ω2={u(t)∈E:‖u‖≤r4,t∈[c,d]}.任意u∈∂Ω2∩K有 因此‖Tu(t)‖≥‖u‖∀u∈∂Ω2∩K. 根据引理8可知T至少有一个不动点,即边值问题式(1)至少有一个正解. 注1若考虑将含两个分数阶导数的零边值问题推广为含n项分数阶导数的情况,目前无法得到形如的解的表达式. 注2若将边值问题式(1)中分数阶的阶数推广为n<α≤n+1,m<β≤m+1 其中,m>1,n>m+1,也即考虑以下边值问题 此时,仍可以通过拉普拉斯变换得到解的表达式,但暂时未能得到类似引理2中格林函数的性质. 考虑下列分数阶微分方程: 其中 解 综上,应用定理1可知边值问题式(11)至少有一个正解.
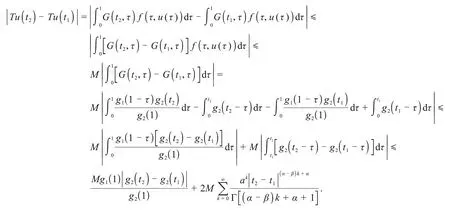

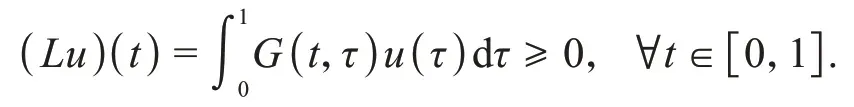
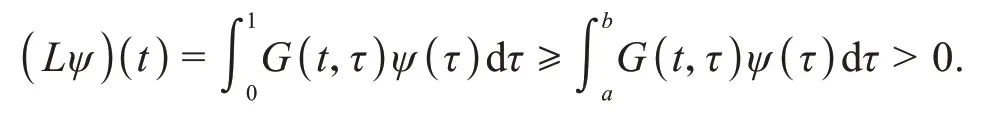
2 主要结果
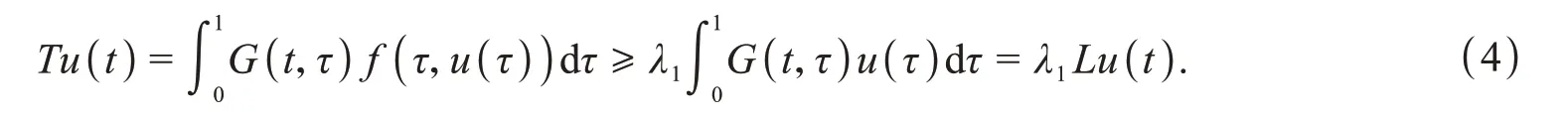
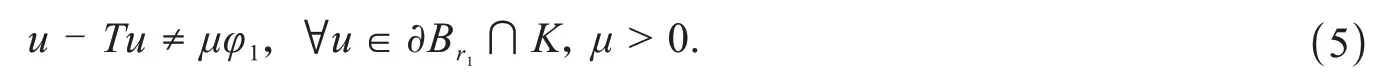
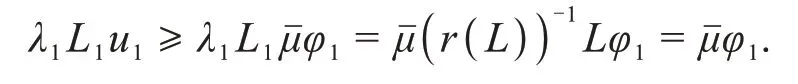




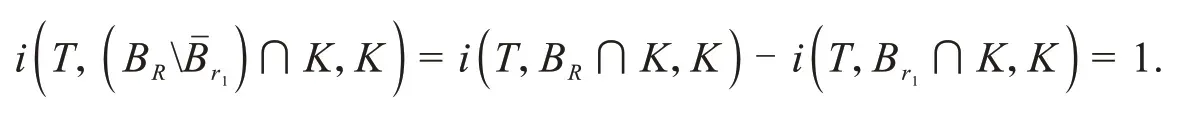
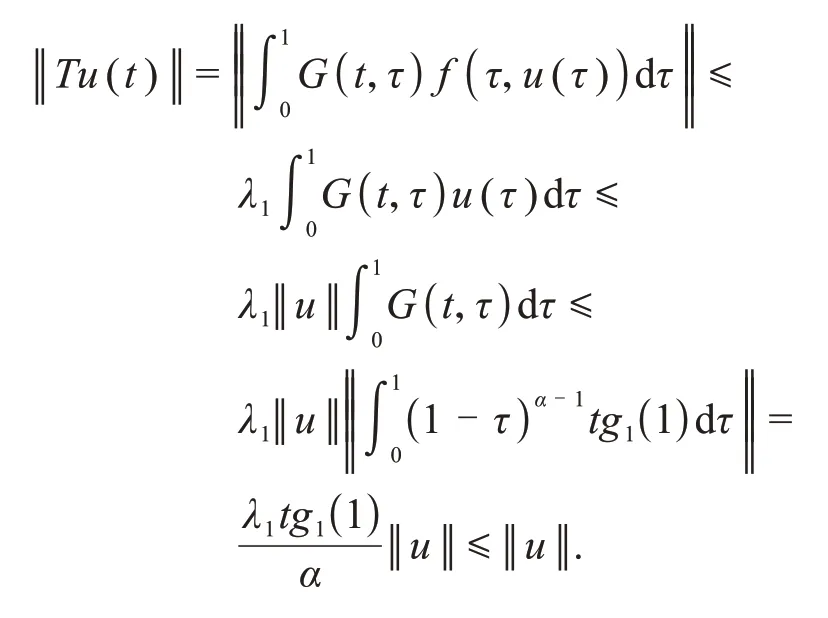
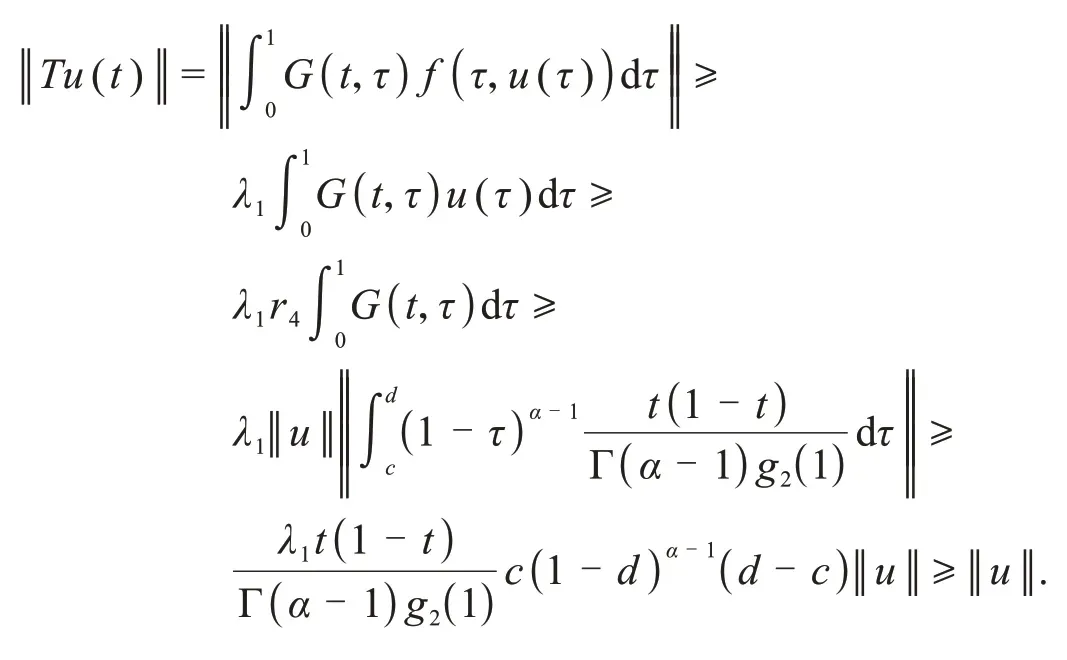
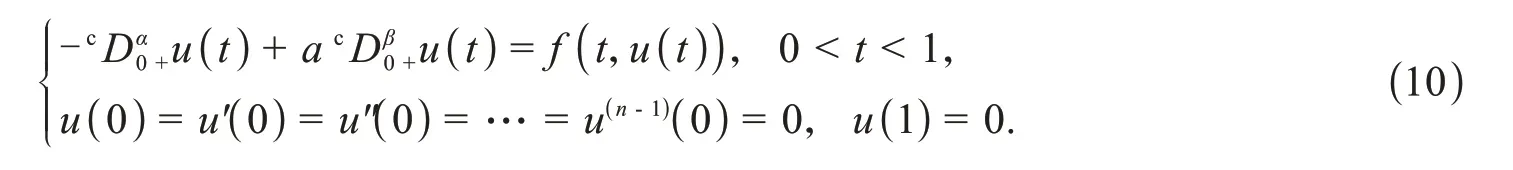
3 实例