热环境下压电功能梯度微板振动特性研究

范世杰，李凤莲

(北京信息科技大学 机电工程学院，北京 100192)

0 引言

功能梯度材料(functionally graded materials,FGM)通常由金属与陶瓷混合而成，具有较好的机械强度、耐热性和抗氧化性，其属性从一个表面到另一表面连续变化，很好地克服了复合材料层合结构应力集中问题。复合材料在电子、机械、通信、航空、航天和交通、医疗等领域得到了大量应用，各领域对性能优越材料的需求也越来越高。压电材料因其独特的正逆压电效应，在智能材料领域发挥着重要作用，将压电材料与功能梯度材料相结合，使其具有独特的机电耦合特性，具有重要的研究意义。

近年来，许多学者针对微结构振动特性进行了大量的深入研究。Majid等[1]基于修正偶应力理论，利用广义微分求积法，研究了不同梁剪切变形理论的S型功能梯度纳米梁的自由振动问题；贺丹等[2]利用高阶剪切理论，建立了Reddy变截面微梁的自由振动模型，分析了尺度效应和横向剪切变形对变截面微梁自由振动的影响；Armagan等[3]针对层合复合材料和夹层微梁，在任意边界条件下的自由振动和屈曲响应进行了研究；Amir等[4]利用Hamilton原理、修正偶应力理论和Kirchhoff-Love壳理论，对尺度参数影响下微双曲壳的固有频率和振型进行了深入的研究；Olga等[5]基于修正的偶应力理论和Kirchhoff-Love板理论，利用R函数理论和Ritz变分法，分析了非经典形状正交各向异性微板的自由振动特性；Yuan等[6]利用谐波平衡法，研究了考虑尺寸效应的含损伤四边固支微板在直流电压下非线性自由振动特性；Mohammad等[7]利用瑞利-里兹法，分析了热环境下不同边界条件对功能梯度微梁的自由振动的影响；Luan等[8]基于修正偶应力理论和高阶剪切变形理论，对功能梯度微夹芯板在机械和热载荷作用下的静态弯曲、自由振动和屈曲行为进行了研究；张大鹏等[9]根据Kirchhoff板理论和非局部弹性理论，建立了黏弹性基体上压电纳米板的热-机电振动特性分析模型，分析了不同参数对其振动特性的影响。

本文根据复合剪切变形理论、Hamilton原理和修正偶应力理论，对热环境下四边简支压电功能梯度微板的自由振动特性进行研究，并讨论了不同参数对系统固有频率的影响。

1 振动理论模型的建立

压电功能梯度微板模型如图1所示，微板的长度为a，宽度为b，芯层厚度为hc，上下面板厚度为hE，微板厚度h=hc+2hE。忽略芯层与上下压电层之间的胶黏层，上、下面板为压电陶瓷材料，中间芯层为功能梯度材料，芯层由陶瓷和金属混合而成，上表面为陶瓷，下表面为金属，其材料属性在厚度z方向上连续变化，Z1、Z2、Z3、Z4为微板z方向坐标，芯层材料中陶瓷的体积分数Vc表示为

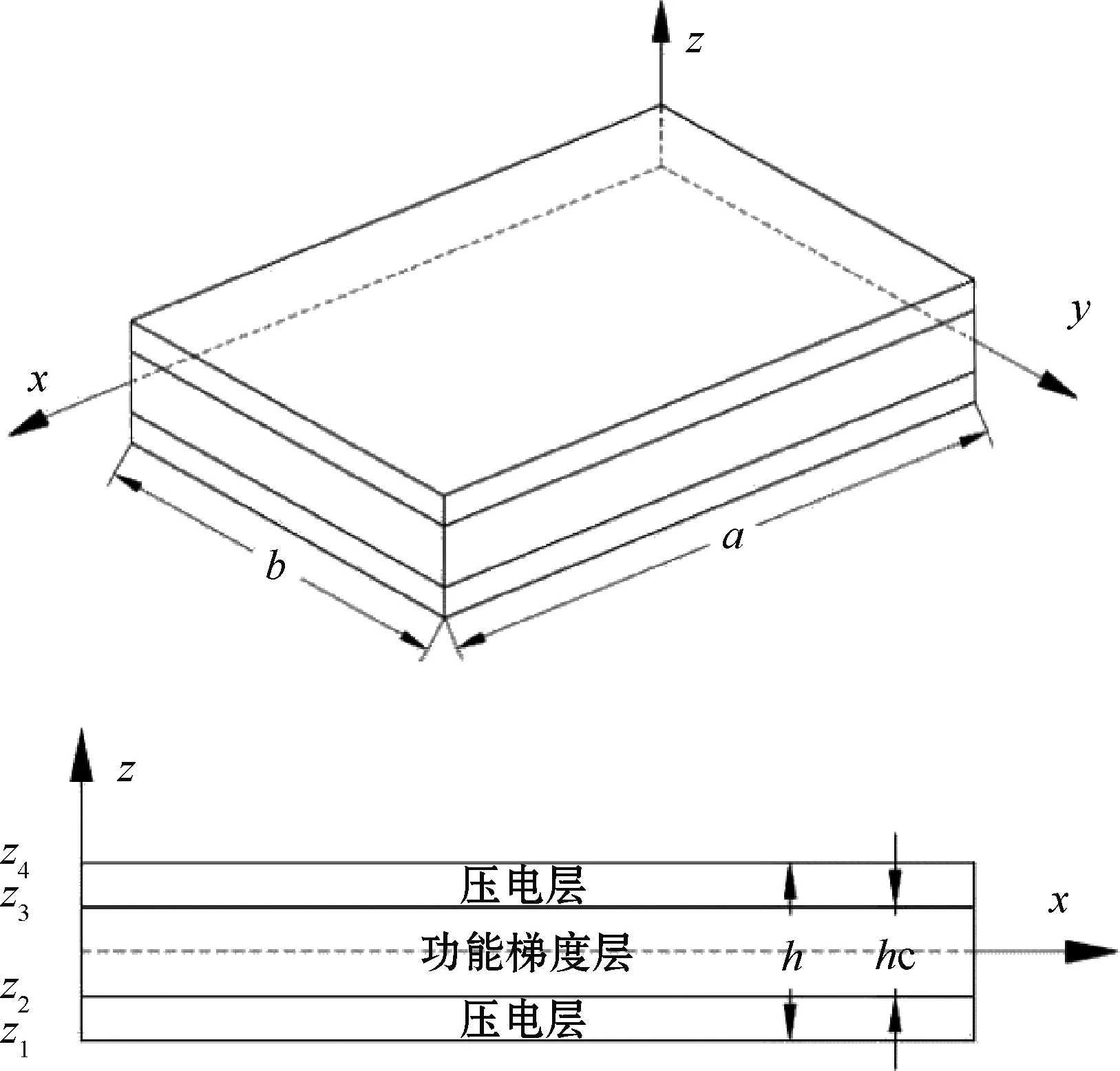
图1 压电功能梯度微板模型

(1)

式中p为梯度指数。

功能梯度材料性质如杨氏模量E、泊松比v、和质量密度ρ等都通过厚度连续变化，材料性能可表示为

Y(z)=YcVc+Ym(1-Vc)

(2)

式中：Yc和Ym分别为陶瓷和金属的材料属性。他们与温度分布的关系[10]可表示为

Yi=Y0(Y-1T-1+1+Y1T+Y2T2+Y3T3)

(3)

式中：i分别为不同材料下标c、m；Y-1、Y0、Y1、Y2、Y3为材料性质立方拟合的常数。

根据一维傅立叶热传导方程，芯层沿厚度方向的温度分布可表示为

(4)

式中K(z)为服从温度分度的导热系数。

Tt为芯层上表面Z3的温度，Tb为芯层下表面Z2的温度。利用多项式幂级数展开式，求解方程(4)，则沿厚度方向的温度分布可表示为：

(5)

(6)

式中：N为收敛性级数项数；Kc、Km分别为陶瓷和金属的热传导系数。

在偶应力理论的发展过程中，不同偶应力理论中材料长度参数性质与数目均不相同，这使得偶应力理论很难在工程中得到广泛应用，Yang等[11]基于经典偶应力理论，提出了只需要一个尺度参数且包含对称偶应力张量的修正偶应力理论，这一理论大大降低了微结构模型的计算难度。根据修正偶应力理论，对称应力张量偏分量Г、对称曲率张量分量ζ可分别表示为

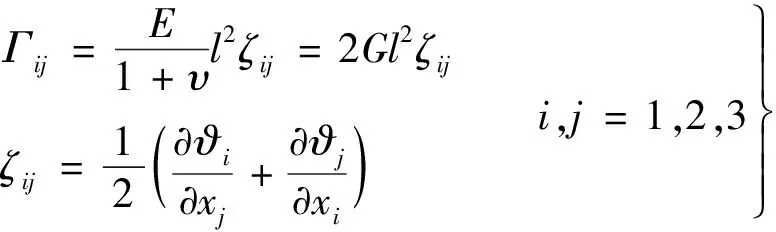
(7)

式中：l为材料长度尺度参数；ϑij为位移场相关旋转向量的分量；G为剪切模量。

考虑横向剪切变形效应，位移场u、v、w和电势函数Φ可以假设为

(8)

基于假设的位移场和电势，根据小变形位移—应变关系得：

(9)

由广义胡克定律，芯层的本构关系为

(10)

式中λ为热膨胀系数。刚度系数可表示为

(11)

根据第二类压电方程[13]，压电材料的本构关系为

式中：H为矩阵转置；c为弹性刚度矩阵；ε为应变向量；e为压电应力常数矩阵；g为介电常数矩阵；D为电位移向量。

只考虑z方向电势分布：

(13)

压电微板的势能、动能和外力功可表示为：

(14)

式中：δU1、δU2、δU3、δU4分别为上压电层应变能、FGM芯层应变能、下压电层应变能以及电势能，可分别表示为：

(15)

根据Hamilton变分原理，压电功能梯度微板的热环境下动力学方程可表示为：

(16)

式中：

q,s=x,y,z

(17)

根据Navier法，四边简支微板的位移分量为：

(18)

求解该矩阵，即可得到功能梯度板自由振动时的固有频率。式中矩阵元素如下所示：

(AT11+AT12)(α2+β2)

k13=-k31=-B11α3-B12αβ2-2B66αβ2+

(BT11+BT12)(α3+αβ2)

DT22)β2

k15=k51=D12αβ+D66αβ-

k16=k61=E31α

(AT11+AT12)(α2+β2)

k23=-k32=(BT11+BT12)(α2β+β3)-

B21α2β-B22β3-2B66α2β

k24=k42=D21αβ+D66αβ-

k26=k62=E32β

k33=-G11(α4+β4)-α2β2(G12+G21+4G66)+

(AT11+AT12)α2+(AT21+AT22)β2-T1(α4+

β4+2α2β2)+(GT11+GT12)(α4+α2β2)+

k34=-k43=L11α3+L21αβ2+2L66αβ2+

k35=-k53=L12α2β+L22β3+2L66α2β+

k36=k63=-(Ez31α2+Ez32β2)

-(RT11+RT12)α2-(RT21+RT22)β2

k46=k64=Ef31α

(RT11+RT12)α2-(RT21+RT22)β2

m11=m22=I0，m13=-m31=-αI1，m14=

m41=m25=m52=J1

m12=m21=m24=m42=m15=m51=

m45=m54=0

m23=-m32=-I1β,m33=-I2(α2+β2)-I0

m34=-m43=K1α,m35=-m53=K1β

m44=m55=J2

式中：

[Aij,Bij,Dij,Gij,Lij,Oij,Rij]=

[T1,T2,T3,T4,T5,T6,T7,T8]=

[ATij,BTij,DTij,GTij,LTij,RTij]=

2 数值计算与仿真

为验证理论模型的正确性，利用有限元软件COMSOL对微板振动进行仿真模拟。

压电功能梯度微板的几何尺寸为：a=352 μm，b=0.7a，板厚h=hc+2hE，压电材料厚度hE=0.2 μm，FGM芯层厚度hc=17.6 μm。压电材料PZT-G1195N的参数为：EE=63 GPa，vE=0.3，ρE=7 600 kg/m3，d=254×10-12m/V，μ=15.3×10-9F/m。FGM芯层材料为陶瓷(Si3N4)与金属(SUS304)混合而成，其材料参数如表1所示。无特别说明，梯度指数p=1，尺度参数l=0.5h。

表1 Si3N4和SUS304温度相关的材料参数

微结构振动特性受尺度参数影响很大，尺度参数影响下理论结果、无尺度参数影响热环境下(△T=0)压电功能梯度微板前8阶固有频率，以及在COMSOL中无尺度参数影响仿真结果对照如表2所示。从表中可以看出，无尺度影响下固有频率理论结果与有限元模拟结果的误差最大为2.42%，验证了理论模型的准确性。有、无尺度参数影响下，系统固有频率数值结果相差较大，且在高阶更加明显，这也可以说明尺度参数对微结构固有频率计算影响很大。

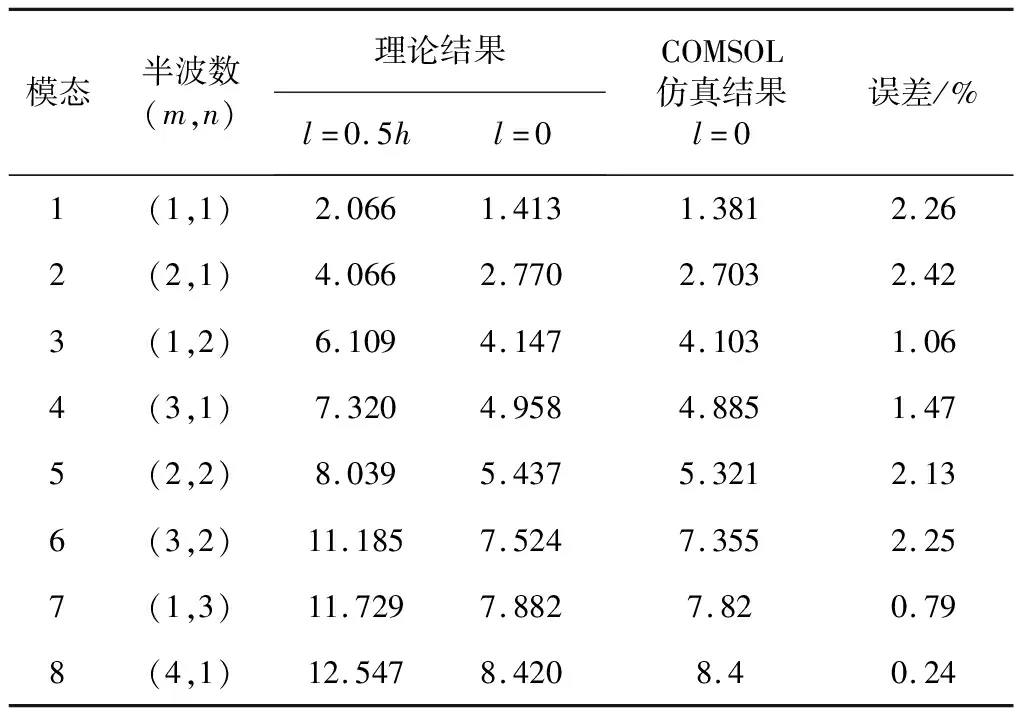
表2 微板理论解与仿真模拟解固有频率对比 MHz

3 参数变化的影响

基于建立的压电功能梯度微板理论模型，在保证其余参数不变的情况下，通过参数变化，分析尺厚比、芯层厚度、压电片厚度与梯度指数对微板系统自由振动频率的影响。

尺度参数是微结构研究中一个重要参数，它对微结构材料的性能影响很大。图2为不同温度下尺度参数对微板固有频率的影响。从图中可以看出，随着尺厚比的增大，系统固有频率稳定增大，在l/h=4后，系统固有频率变化速率减弱，即板厚较小时，尺度参数影响较大。但是温度变化对基频影响较小。

图2 不同温度下尺厚比对系统固有频率的影响

FGM作为微板的主体材料，其厚度变化对整个结构的性能有着很大的影响，图3为不同温度下芯层厚度对微板固有频率的影响。从图中可以看出，随着芯层厚度的增大，系统固有频率整体变化趋势一致，都逐渐增大，且增幅较快。

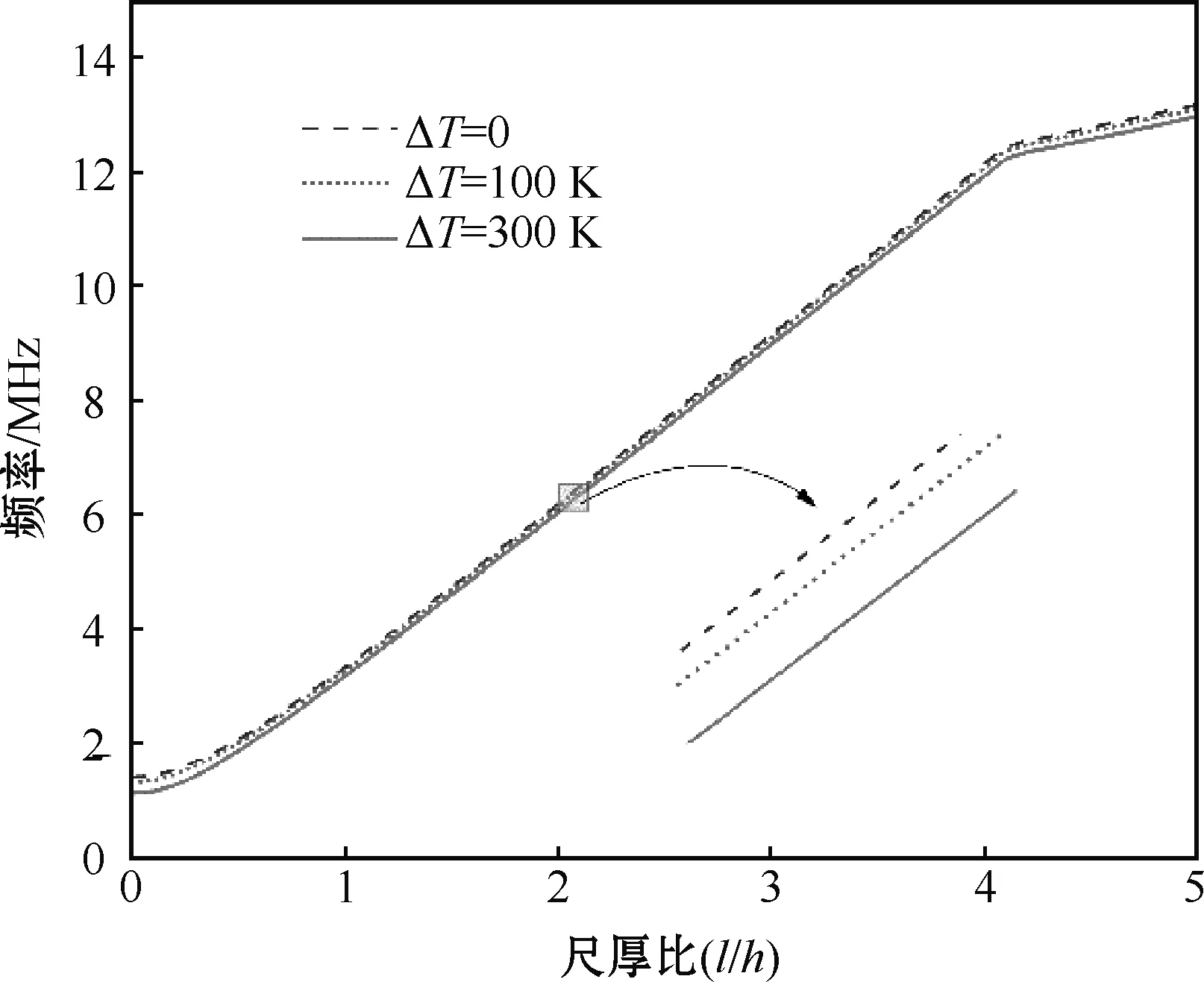
图3 不同温度下芯层厚度对系统固有频率的影响

压电材料是智能结构中传感与驱动最常用的材料，压电片厚度变化将改变电场对整体结构性能的影响，图4为不同温度下压电片厚度对微板固有频率的影响。可以看出，随着温度增高，固有频率降低；随着压电片厚度增大，系统固有频率稍有增大，但整体变化幅度较小，变化范围在0.25～0.3 MHz，在变化过程中稍有一些波动，这是由于压电层与功能梯度层之间的变形，在计算时进行了忽略引起的。

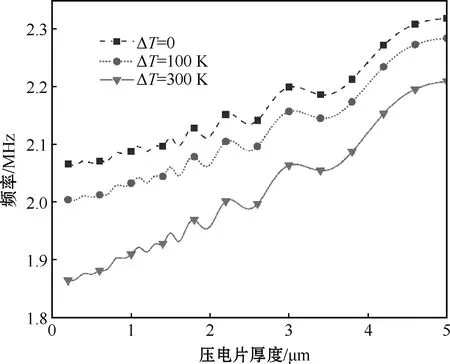
图4 不同温度下压电片厚度对系统固有频率的影响

功能梯度材料的梯度指数改变，即FGM混合材料的分布方式发生变化，使得结构整体的刚度发生改变，进而影响到整个系统的振动特性，图5为不同温度下功能梯度指数对微板固有频率的影响。从图中可以看出，随着梯度指数的增大，不同温度对固有频率的影响逐渐降低，固有频率整体变化趋势一致，迅速减小后逐渐稳定在某一频率附近。

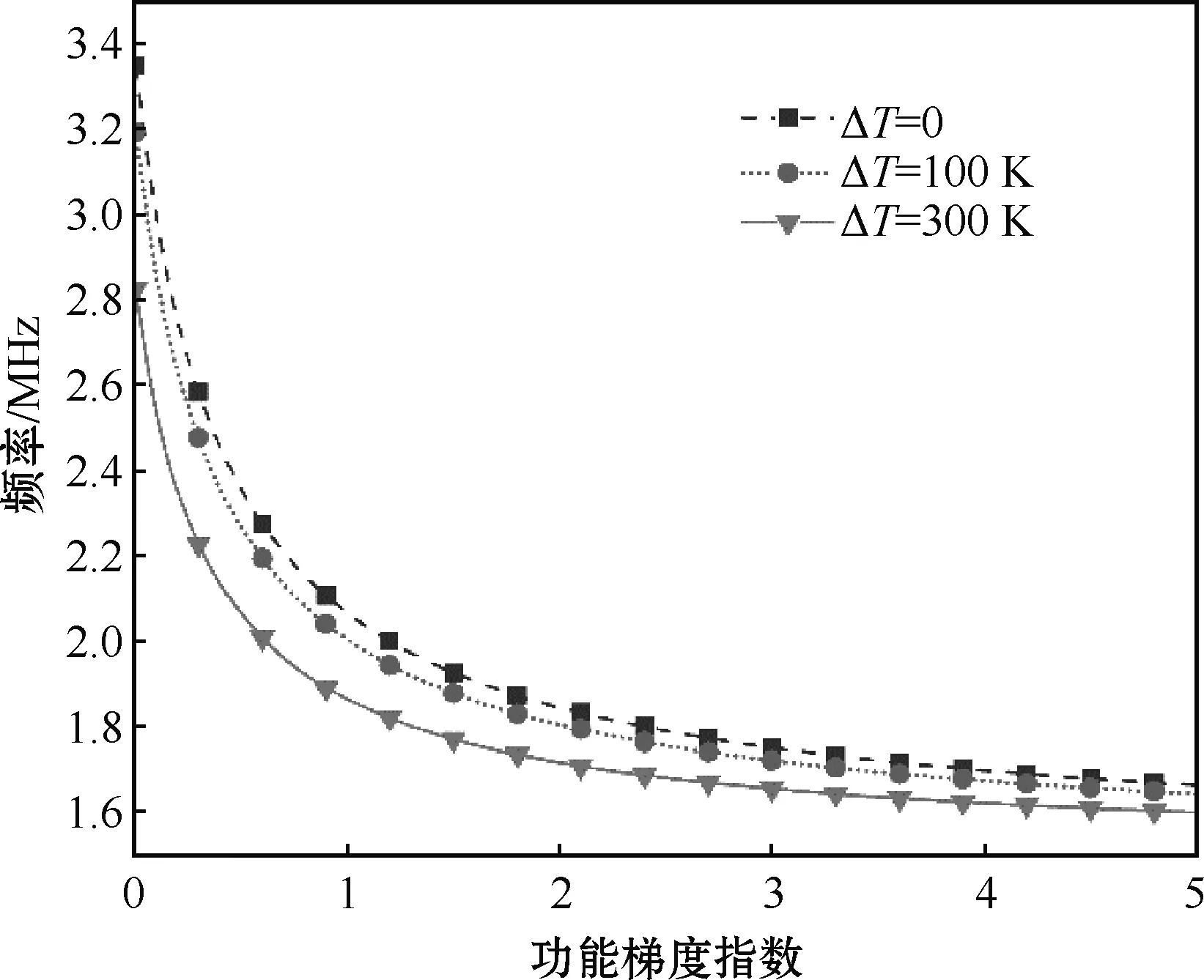
图5 不同温度下功能梯度指数对系统固有频率的影响

4 结束语

本文基于修正偶应力理论和复合剪切变形理论，根据Hamilton原理建立了热环境下压电功能梯度微板的动力学理论模型，通过有限元仿真模拟，验证了理论模型的正确性。在此基础上，分析了参数变化对整个系统振动特性的影响。在不同温度下，尺厚比增大与芯层厚度增大，系统固有频率迅速增加且增幅较大；功能梯度指数增大，固有频率迅速减小后趋近于某一频率附近，而压电片厚度的增加使得系统固有频率不断波动上升，且固有频率变化幅度较小。