船体变形对海上升压站上部组块海运设计的影响

史政，陈桂举，梁金放

（中国能源建设集团广东省电力设计研究院有限公司，广东广州 510663）

0 引言

根据规范《海上固定平台规划、设计和建造的推荐作法》（API RP-2A-WSD）［1］可知：海运设计是上部组块重要的设计工况，设计原则可以参考API RP 2MOP［2］和GL 0030/ND［3］规范，国内也可参考《海上拖航指南》［4］执行。其中以GL 0030/ND应用更为广泛，其详细推荐了海运设计应考虑的环境荷载、设计工况等的最低要求，尤其在项目前期缺乏具体运输信息时指导意义重大，可操作性强，因此海工行业广泛参考GL 0030/ND 规范进行海运设计。

随着海工行业的发展，上部组块越来越大型化、重型化，根据规范简化的最低要求进行海运设计逐渐不能适应海工行业的复杂情况，上部组块的结构设计需深入研究。

1 按规范进行海运设计

1.1 海运设计的环境荷载及工况

上部组块在海运工程中，主要荷载来自船体晃动，船体晃动包括6 个自由度的运动，参考《钢制海船入级规范》第2 篇船体［5］的1.5.1.9 小节定义，船体坐标如图1所示。

图1 船体坐标Fig.1 Ship coordinate

船体运动定义如下：

1）横摇（Roll）：绕X轴转动；

2）纵摇（Pitch）：绕Y轴转动；

3）艏摇（Yaw）：绕Z轴转动；

4）纵荡（Surge）：沿X轴平移；

5）横荡（Sway）：沿Y轴平移；

6）垂荡（Heave）：沿Z轴平移；

上述6 个运动是相互关联的，关系较复杂。其中，横摇、纵摇、垂荡3 个运动幅值较大，在3 个方向的平移运动分量中所占比重较高，故可简化为横摇、纵摇、垂荡3个运动。根据GL 0030/ND Section 7.9.1 Table 7-1，环境荷载考虑角幅值、周期及加速度如下：

1）横摇：±20°，T=10 s；

2）纵摇：±12.5°，T=10 s；

3）垂荡：±0.2 g。

其中，g 指重力加速度，上述取值根据具体的航区及船型情况会有调整。

一般考虑如下8个工况：

±横摇±垂荡；±纵摇±垂荡。从上述规范做法可知，船体变形未被考虑，实际上规范做法也多是假设船体为刚体。

1.2 船体总纵强度和船体实际运动

根据《钢制海船入级规范》第2 篇船体第2 节可知：船体总纵强度包括满足静水弯矩和剪力、波浪弯矩和剪力，而船舶在海运中6 自由度运动的主要来源就是波浪，故船体总纵强度可理解为船体在各种装载情况下抵抗波浪荷载的能力，即船体结构在中拱（Hogging）和中垂（Sagging）状态下的强度问题，具体可参考规范DNVGL-OS-C102［6］3.8.1小 节或《CCS 船体结构疲劳强度指南》［7］2.4.1小节。

由上述船级社规范可知：船体在运输时，船体梁一直处于中拱或中垂两个变形状态。

2 船体变形计算

2.1 船体梁变形的理论计算

运输船资料已有的情况下，根据《船舶结构力学》［8］2.1.2小节，船体梁的微分方程为：

式中：

E——船体梁材料杨氏模量（Pa）；

I——船体梁的惯性矩（m4）；

v＇＇——船体梁竖向相对位移的二次导数（m-1）；

M——海运工况时的船体梁计算截面对应的弯矩（N·m）。

根据船体梁强度和变形关系［9］，船体梁弯曲半径R为：

R的单位为m。基于公式（2）的半径，结合基本几何公式，可得模块各支座位置的水平、垂向相对变形，变形如图2所示（以中拱为例）。

图2 船体中拱变形Fig.2 Hull deformation at Hogging

2.2 船体梁变形的简化算法及变形极值

一般在设计上部组块时，运输船资料未知，故理论计算方法一般不适用。但是参考类似项目，运输船的主尺度（船长L、船宽B、型深D、吃水H，单位为m）可以确定。基于主尺度信息，采用简化算法，可以计算出船体梁变形的极值。根据船体梁变形、应变关系相关公式得：

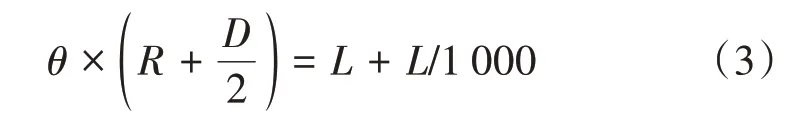
根据基本几何概念：圆心角θ=L/R，可得：

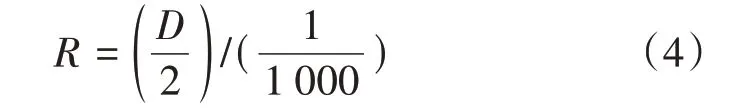
由公式（4）知：船体梁中性轴弯曲半径R主要和船体型深D有关，并且船体弯曲半径远大于船体型深，即：R≫D，故船体甲板单位弧长产生的弧长变形可作为甲板水平变形。

根据《材料力学》［10］的应力、应变关系，有如下公式：

式中：

ε——应变；

σ——材料应力（Pa）。

根据《钢制海船入级规范》第2 篇船体1.3.1.7小节甲板许用应力为：

式中：

Fy——材料屈服强度（Pa）；

K——规定的材料系数。

结合公式（3）至公式（6）及图3 的基本几何关系：中拱时以上部组块中点为参考原点，船体甲板单位弧长产生的变形为：

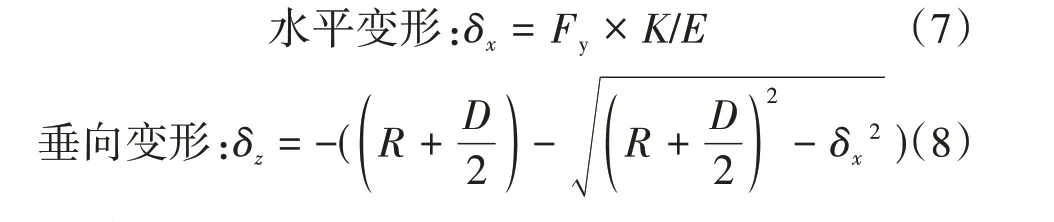
代入Fy=235～460 MPa，K=1.0～0.62，E=206 GPa，得到δx=(1.14～1.38) × 10-3。考虑到简化计算比较保守，国外一些海洋工程公司实际应用时取0.001［9］。

同理，中垂时以上部组块中点为参考原点，船体甲板单位弧长产生的X轴方向的变形为：δx=-0.001。

结合实际取值及本文公式（4）和公式（8）可知：船体梁变形简化计算时，变形只与船体型深D有关。因为船型一般为标准化设计，所以在海工模块尺寸和重量已知的情况下，可根据海运经验确定运输船的排水吨位（主尺度），进而确定型深D的范围来进行简化计算。

3 工程应用实例

笔者设计的多个海上升压站，在考虑运输船的船体变形影响后，上部组块首层与海运相关的主结构均出现应力显著增加甚至强度不够的情况，应力增加位置均在绑扎件附近。本文以某300 MW 项目作为工程实例进行计算分析。

3.1 计算输入

该项目海上风电上部组块基本情况如下：

1）海运绑扎布置如图3所示。轴2、轴4 间距为19.4 m，平行于船长方向；轴B、轴F 间距为24.0 m，垂直于船长方向；绑扎件连接于首层甲板主梁/主柱交点处，绑扎件与甲板夹角≥45°。

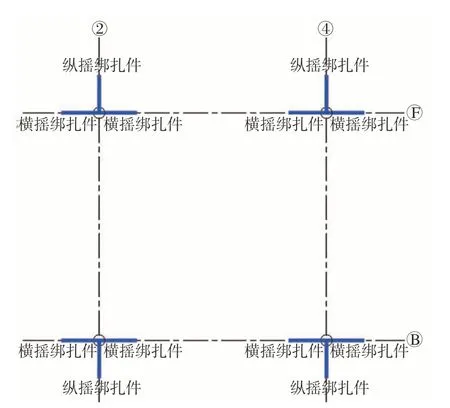
图3 绑扎件布置图Fig.3 Sea fastening layout

2）首层甲板与垫墩顶部高差为4 m，垫墩顶部距离运输船甲板高差约为2 m。

3）运输船型深考虑为8.6 m，根据本文公式（4）的船体梁中性轴半径为R=4 300 m。

4）船体材料保守考虑为Fy=335 MPa。

5）所有支撑点的边界条件设置为铰接。

以轴B、轴F 之间中点为参考原点，按本文原理计算中拱荷载如表1所示。

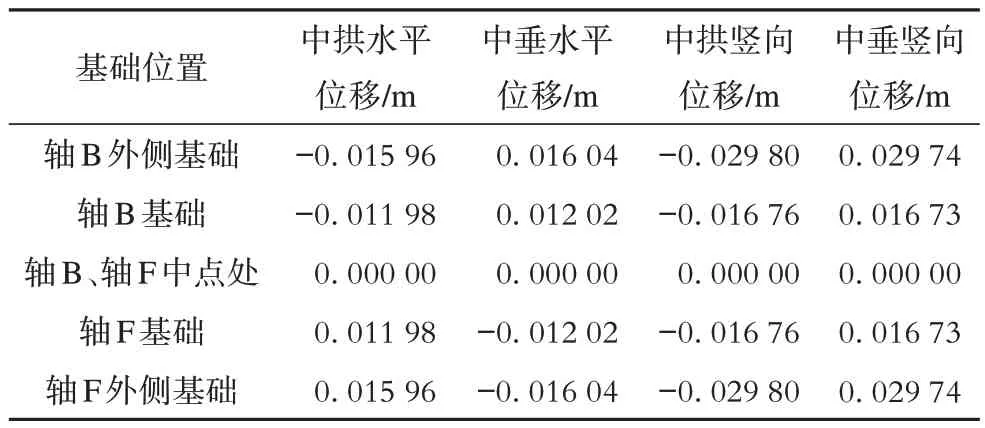
表1 中拱、中垂绑扎件基础位移Tab.1 Deflection of Sea fastening support in hogging/sagging

3.2 结果对比

本文共考虑3套工况组合，用3个模型实现：

1）常规无中拱、中垂荷载的工况组合；

2）将中拱、中垂荷载分别与1）中的工况组合再进行组合；

3）将中拱、中垂荷载分别考虑50%再与1）中的工况组合进行组合。考虑该工况的原因：规范推荐的海况比较保守，实际海运时会根据天气预报避开大风浪，即按规范计算的海运荷载实际有折减，根据某些运输单位反馈取50%。

中拱、中垂荷载主要影响绑扎件附近主梁、主柱、首层纵向斜撑，3 套工况组合结果汇总如表2所示。

从表2的结果可知：

表2 海运计算结果对比Tab.2 Result comparison for sea transportation

1）不考虑荷载折减，绑扎件附近主梁、主柱应力增量均为+60%，因此，与绑扎件相连的主梁、主柱应有较大的强度储备，才能满足实际的海运工况。考虑该影响后，笔者参与设计的海上升压站上部组块首层部分主梁一般用到H1 200×500 左右的型钢，普遍比其它设计院用的H1 000×400型钢大。

2）首层纵向斜撑应力增量相对较小，说明基础船体变形主要被绑扎件附近的主柱、主梁吸收。同时应注意，斜撑应力增量比例也与整体结构布置有关。在本工程中，无斜撑与绑扎件所在节点直接相连，故影响较小。

3）纵向绑扎件应力提高最为明显，可达原来的4 倍左右。结合本文图3，总结其原因是：船体梁的水平刚度≫海运模块的水平刚度≫绑扎件的水平刚度，船体梁的变形直接被绑扎件吸收，因此对绑扎件的影响最大。

另据笔者计算可知：采用本文图3 所示普遍采用的绑扎方案（纵向两端设绑扎件），提高纵向绑扎件截面不能有效降低杆件应力值，应考虑改进绑扎方案。

4 海运绑扎的改进建议

4.1 减少纵向绑扎件的排数

根据《海上拖航指南》附录1 第2.1、2.2 节公式，结合船型、绑扎布置的经验取值，可得海运模块的横摇、纵摇加速度数值范围为：

横摇：0.5～0.8 g，结合经验一般可取0.6 g

纵摇：0.2～0.4 g，结合经验一般可取0.3 g

可见，纵摇加速度较小，约为横摇加速度的50%，而船体梁的基础变形主要来自纵向，因此考虑适当减少纵向绑扎件的排数，结合本文项目实际工程情况，改进后的绑扎布置如图4所示。

图4 与图3 相比可以看出：图4 在纵向只有一排纵向绑扎件，相当于船体梁传递给纵向绑扎件的变形荷载被释放掉了。海运计算结果对比如表3 所示（只对比考虑100%船体变形结果）。

图4 改进后的绑扎件布置图Fig.4 Improved sea fastening layout

从表3的结果可知：

表3 改进后的海运计算结果对比Tab.3 Result comparison for improved sea transportation

1）主梁应力增量与减少纵向绑扎件之前几乎相同。其原因是：模块支座仍受纵摇荷载。但经过笔者详细对比发现有区别：改进前，在2 排纵向绑扎件附近都有高应力区；改进后，只在纵向绑扎件附近有高应力区，即高应力区随着纵向绑扎件的排数减少而减少。

2）主柱应力增量相对值较大，应力比值＞1.0。其原因是：在减少纵向绑扎件一侧，模块支座仍受船体纵向和垂向荷载，且荷载全部由该侧的主柱承受，但适当增加主柱截面或者局部加强即可满足强度设计要求。

3）首层纵向斜撑应力增量较大。其原因是：模块全部纵向加速度产生的荷载全部由一侧斜撑承受，但是截面仍满足强度要求。

4）绑扎件应力增量减少了约50%，但仍远不能满足强度要求。其原因是：模块支座、绑扎件之间仍有相对位移荷载。

5）总体而言，减少纵向绑扎件后，模块受力情况反而改善了。

4.2 模块固定采用滑动支座

笔者推荐的典型滑动支座如图5所示。

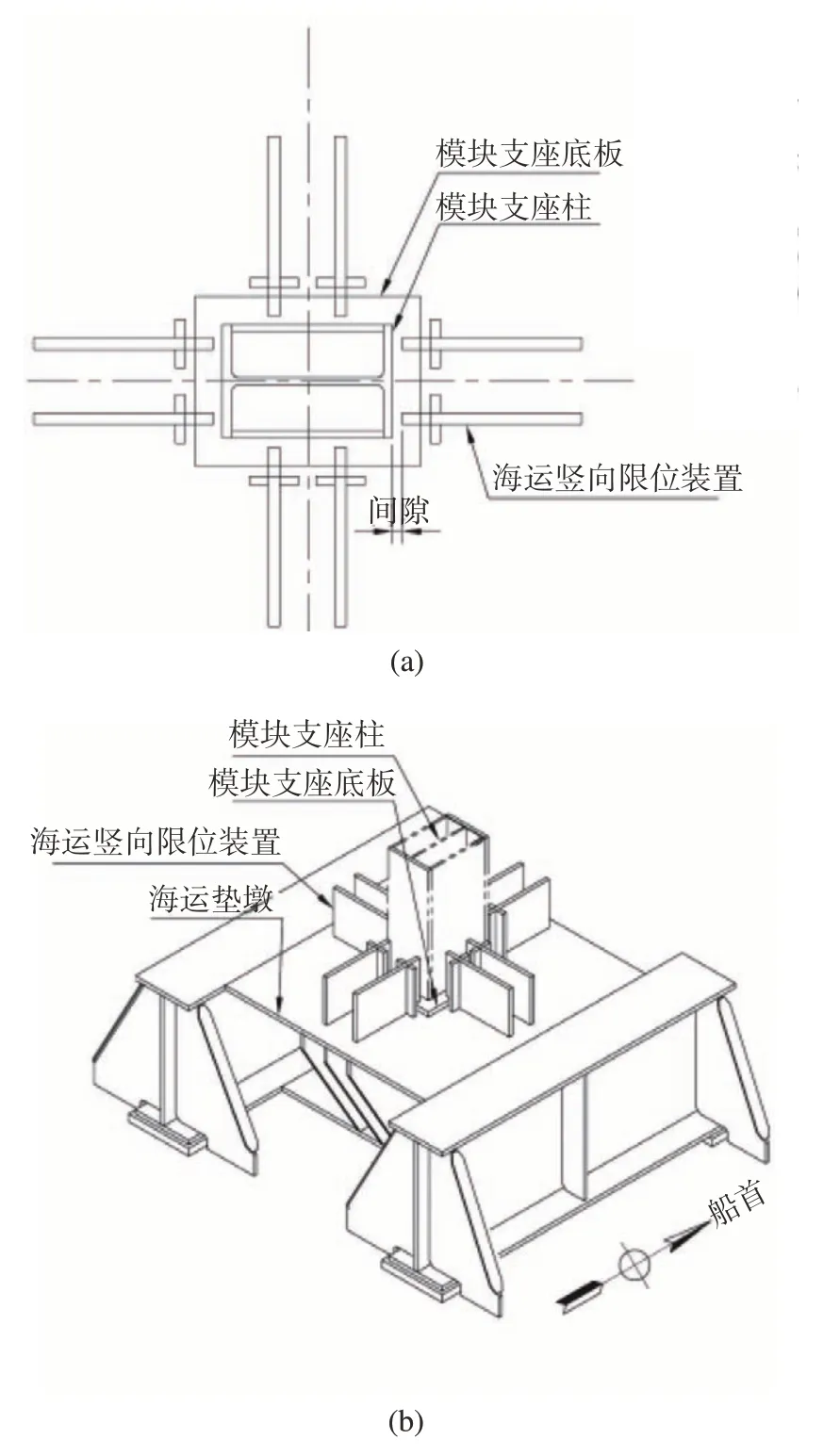
图5 典型海运滑动支座Fig.5 Typical sliding bearing

图5所示滑动支座设计原则如下：

1）模块支座与海运垫墩之间只限制竖向位移，水平方向是滑动的，水平间隙值根据本文中公式计算可得到，一般可考虑25 mm。

2）纵向加速度产生的荷载全部由单排纵向绑扎件承担。对于超大型模块，考虑到船体甲板承载力，可适当增加几组纵向绑扎件。

3）采用滑动支座，船体梁产生的竖向荷载仍需考虑。

采用本文4.1、4.2 节的措施，包括文中300 MW 项目在内的多个项目的海上升压站上部组块在海运时考虑船体梁变形后，均能满足强度设计要求。

5 结论

对于海洋工程，模块的海运工况是主要控制工况之一，目前国内海运设计时将船体作为刚体，仅考虑海运加速度荷载，未考虑船体变形的影响，而船体变形必然发生，因此，船体假设为刚体不合理，船体变形必然对上部组块在海运工况时产生影响。然而，船体变形大小取决于船舶装载情况和风浪的大小，故船体变形的实际值在设计阶段是不确定的，可结合项目海运要求和本文推荐方法进行考虑。

基于本文分析，对于海洋工程的海运设计方案建议如下：

1）海运工况应考虑船体变形对模块的影响，前期设计缺乏资料时可采用本文推荐的方法，对于较复杂的海工模块，应与船体整体建模计算海运工况。实际海运一般避开恶劣海况，大部分船舶姿态监测结果显示：船舶摇晃幅值和船体变形一般小于理论计算值的50%。因此，在躲避恶劣海况的条件下，船体变形荷载（本文2.2 节）可只考虑50%（无限航区考虑100%）；但船舶摇晃幅值应按《海上拖航指南》（简化结果见本文4.1节）考虑100%。

2）对于未考虑船体变形影响的海运设计，受海运绑扎件直接影响的区域，主要结构杆件应留较大的强度储备，结合本文工程案例推荐50%以上；次要结构杆件可通过改变结构布置或构造措施，避免次要构件与绑扎件节点域直接相连，减少船体变形荷载的影响。

3）模块与支墩的连接，应尽量采用本文4.2 节推荐的滑动支座方案，减轻船体纵向变形。

4）对于海运绑扎方案，应尽量减少纵向绑扎件的数量，减少船体纵向变形的影响。