计及多能流不确定性的综合能源系统优化配置

高统彤 邵振国 陈飞雄

计及多能流不确定性的综合能源系统优化配置

高统彤1,2邵振国1,2陈飞雄1,2

（1. 福州大学电气工程与自动化学院，福州 350108； 2. 福建省电器智能化技术研究中心，福州 350108）

综合能源系统存在较大的运行不确定性，规划过程中忽略这种不确定性会导致设备配置容量过于理想化、设备利用率低的问题。针对此问题，本文采用仿射变量建立综合能源系统协同规划模型，将仿射优化模型分解为目标仿射函数的中心值最小及在不确定性因素影响下仿射函数变化量最小两个子问题，前者为仅考虑源荷预测功率的确定性优化模型，后者考虑源荷预测误差，通过max模型和min模型交替迭代，使配置结果受不确定性因素影响最小。采用某园区综合能源系统规划算例验证所提方法的有效性和经济性。

综合能源系统；规划；能量枢纽；不确定性；仿射优化

0 引言

风-光-冷热电联供系统能合理利用可再生能源，并通过能量梯级利用提高能量利用效率，减少污染物排放[1-2]。然而，可再生能源的随机性、间歇性、波动性和负荷的不确定性会影响综合能源系统的经济运行[3]。在进行综合能源系统规划时，若不考虑风光出力和负荷的不确定性，会造成系统容量配置过于理想化、设备利用率低等一系列问题[4]。因此，计及多重不确定性的园区微能网协同规划已成为国内外学者的研究热点。

在园区微能网规划问题中，处理综合能源系统不确定性问题的主要方法有概率法[5]、鲁棒优化[6]和区间优化[7]等。概率法需要获取不确定变量准确的概率密度函数，而区间优化和鲁棒优化只需获取不确定变量的波动区间，在缺乏统计信息时具有良好的工程应用价值。相比于区间优化，鲁棒优化方法侧重于考虑极端情况，要求在最坏情况下满足约束条件，其结果偏于保守[8]。

文献[9]建立了以综合能源系统的投资成本、运行成本和碳交易成本之和最小为目标的规划模型，并利用两阶段鲁棒优化模型应对电负荷、热负荷和电-热可转移负荷的不确定性。文献[10]根据历史/预测年8 760h多能负荷数据，通过K均值聚类分群方法得到多个典型日负荷场景，以上下界区间描述负荷不确定性，形成鲁棒规划模型。针对鲁棒优化保守性较大的问题，文献[11]提出区间优化法。文献[12]针对综合能源系统规划运行时缺乏对负荷、可再生能源预测误差和购能价格波动不确定性的考虑，构建了基于粒子群优化-区间线性规划的双层优化模型。文献[13]用概率分布函数描述系统中可再生能源发电预测的不确定性，用区间数描述负荷预测不确定性，由此构建了区间线性随机机会约束规划模型，但是设备的优化运行功率和经济成本均为区间，在区间长链计算中，经区间算术运算所得到的区间范围往往比实际范围大得多[14]。

仿射算术比区间算术的保守度小[15]，能够跟踪不同因素对综合能源系统的影响。文献[16]采用基于仿射运算的区间线性规划对模型进行求解，有效改善了区间运算过于保守的问题，但是仿射运算仅用于模型求解的加减法，而乘除法仍然采用区间运算。文献[17]提出日前优化和日内优化相结合的方法，基于仿射算法研究综合能源系统的优化控制，考虑最极端的情况将模型中的不确定性约束条件转化为确定性约束，会导致求解结果的保守性增加。

针对上述考虑不确定性的综合能源系统规划方法的不足，本文建立基于仿射的优化配置模型，将优化配置模型拆分成两个子问题，分别最小化年总综合成本的中心值及不确定性因素导致的年总综合成本变化量。前者为仅考虑源荷预测功率的确定性优化模型；后者以不确定性导致的年总综合成本变化量最小为上层优化目标。下层为最恶劣情况下（max问题）的运行成本最小化问题（min问题），采用max模型预测源荷功率误差，采用min模型校正储能设备功率、园区与上游能源网络的交互功率。通过下层两个模型的交替迭代，降低保守性。叠加两个子问题的求解结果，获取能在极端情况下运行且受不确定性因素影响最小的设备容量配置方案。相比鲁棒优化方法，本文方法在降低成本的同时，提高了设备利用率，最后通过算例验证了方法的合理性及有效性。

1 综合能源系统

能量枢纽（energy hub, EH）作为综合能源系统的耦合点和各能源载体的转化站，将各个能源环节与信息等支撑系统有机融合。典型的EH基本框架如图1所示，其中微型电系统包含光伏发电装置、电储能设备（electric storage, ES）、电锅炉（electric boiler, EB）、热电联产设备（combined heat and power, CHP），微型热系统包括热电联产设备、燃气锅炉（gas boiler, GB）、热储能（heat storage, HS）装置，微型气系统包含热电联产设备、燃气锅炉等。EH从上游的电网公司和天然气公司购买电能和天然气，合理分配给各个能源转换和储存装置，使各个微型系统的能量达到平衡，并满足用户侧的电、热、气负荷需求。

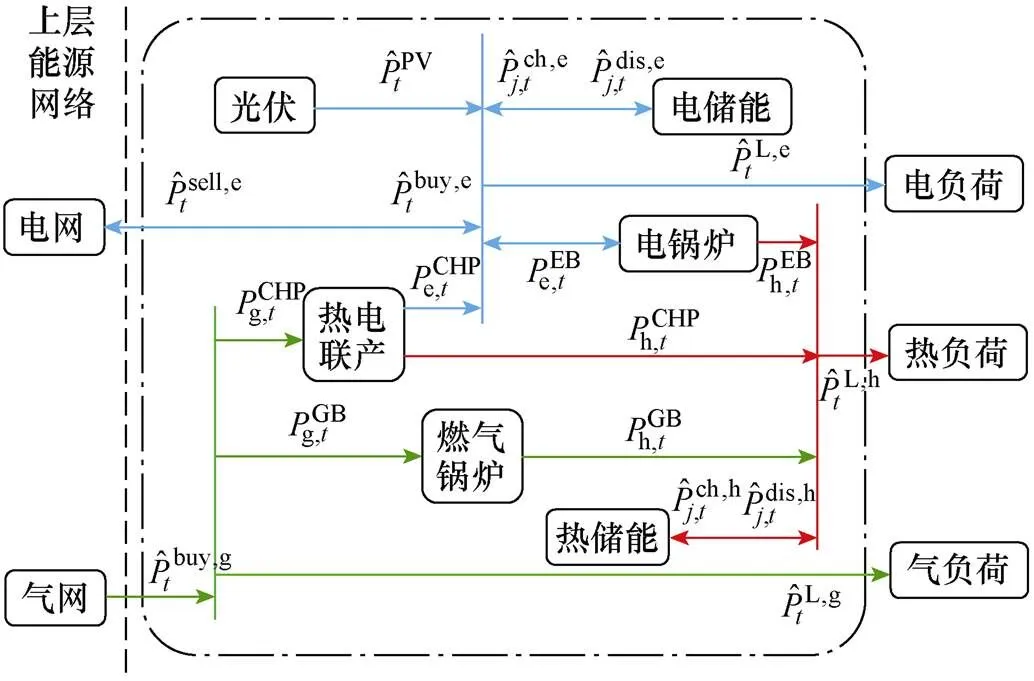
图1 典型EH基本框架

对EH建模，考虑储能装置，图1中的EH输入输出的耦合关系为

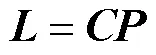
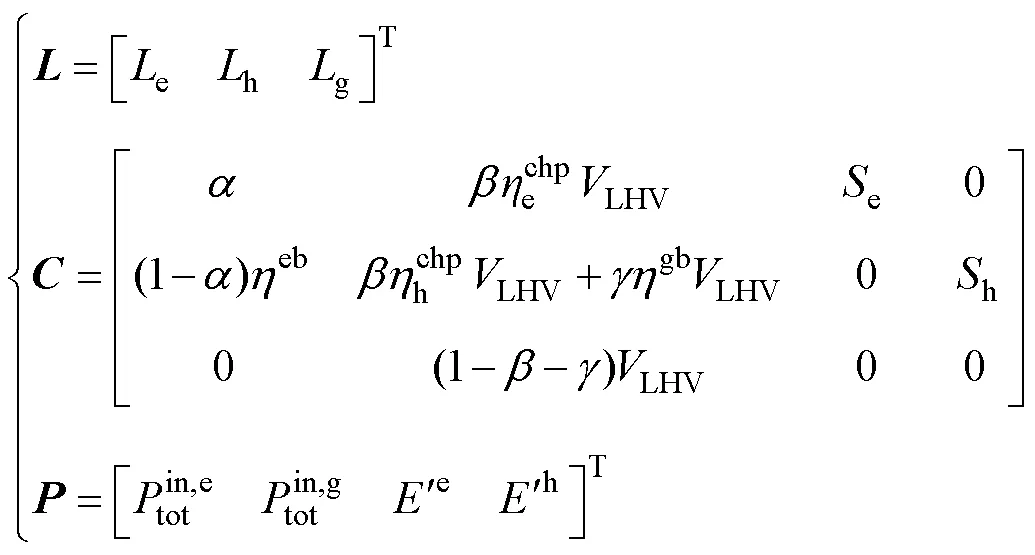
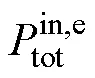
2 基于仿射的综合能源系统不确定性分析

2.1 仿射算术

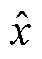
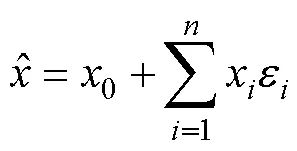
基本的仿射运算法则详见文献[18]，乘法、除法、倒数、平方运算会产生新的噪声元。

2.2 综合能源系统不确定性仿射建模

在综合能源系统运行的过程中，由于气象和物理等因素的影响，风电、光伏输出功率，电、热及天然气系统的负荷具有不确定性，本文用仿射描述这些不确定变量，所建立的风电、光伏、负荷的仿射模型分别为

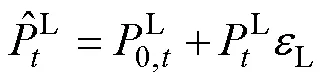
由于储能设备功率及园区与上游能源网络交互功率能够迅速、灵活地变化，所以可通过改变其功率以适应源荷功率变化，从而维持园区功率平衡[19]。

考虑在园区实际运行中，源荷功率存在预测误差。因此，储能设备出力及园区与上游能源网络交互功率也会随之产生波动。式（9）和式（10）即为根据源荷功率预测误差建立的储能设备功率、园区与上游能源网络交互功率的仿射表达式。

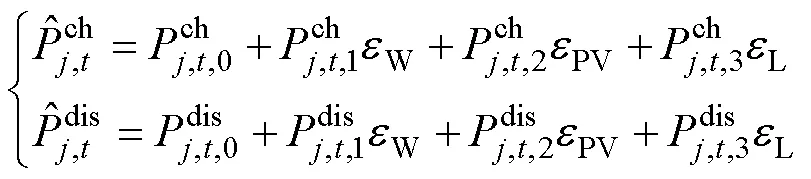
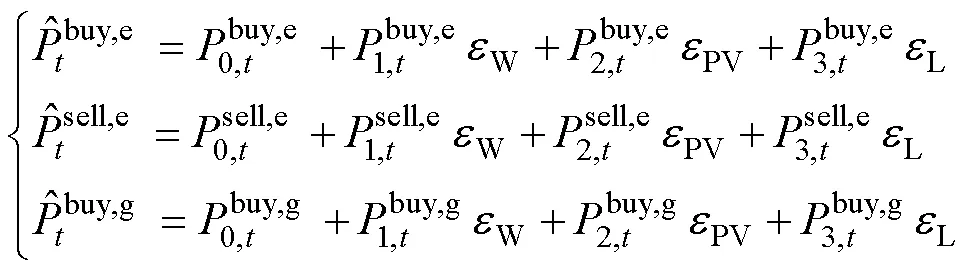
3 计及不确定性的优化配置模型

3.1 优化配置的两个子问题

仿射优化问题的一般形式为

在综合能源系统优化配置的目标函数中，考虑决策变量中含有风电、光伏和负荷三者的噪声元，则优化配置的年总综合成本可以写成

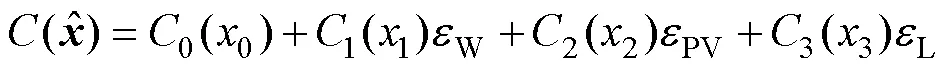
子问题1为确定性优化配置，优化风电、光伏、负荷功率均为预测值时园区中各设备配置容量。通过确定性优化求得的储能功率、园区与上游能源网络交互功率作为子问题2对应功率的仿射中心值。

子问题2为不确定性优化配置。由于储能设备功率及园区与上游能源网络交互功率能够迅速、灵活地变化，所以可通过改变其功率以适应源荷功率变化，从而维持园区功率平衡。储能设备的功率不同，所配置的容量也需要随之变化。

不确定性优化模型根据源荷预测误差调整储能设备功率、园区与上游能源网络的交互功率，优化因源荷预测误差所导致的储能容量变化量，从而最小化不确定性因素导致的年总综合成本变化量。优化模型的约束条件中含有储能功率、园区与上游能源网络交互功率的仿射形式，如式（9）和式（10）所示。仿射的中心值需由确定性优化求得。叠加两个子问题的优化结果，得到综合能源系统优化配置方案。

确定性优化模型和不确定性优化模型均为双层，具体如下。

3.2 双层优化模型

1）上层规划模型

确定性优化模型的上层以年综合成本最小为目标函数，决策变量为各类设备的安装容量。不确定性优化模型的上层以源荷预测误差导致的年总综合成本变化量最小为目标函数，决策变量为不确定性引起的储能设备容量变化量。

确定性优化模型的上层目标函数为

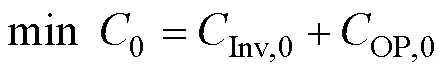
不确定性优化模型的上层目标函数为

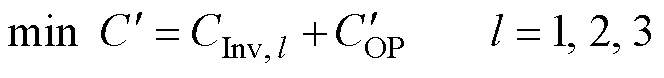
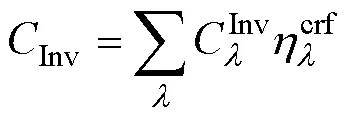
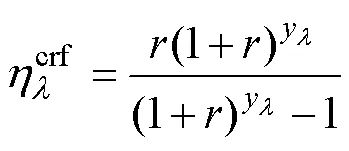
式中：为折现率；为类设备的使用年限。

2）下层优化模型

两个子问题的下层均为优化调度模型。确定性优化模型的下层以园区运行成本最小为目标函数，决策变量为设备各个时刻的功率值。不确定性优化模型的下层以园区运行成本变化量最小为目标函数，决策变量为不确定性引起的储能设备功率变化量及园区与上游能源网络交互功率变化量。

确定性优化模型的下层目标函数为

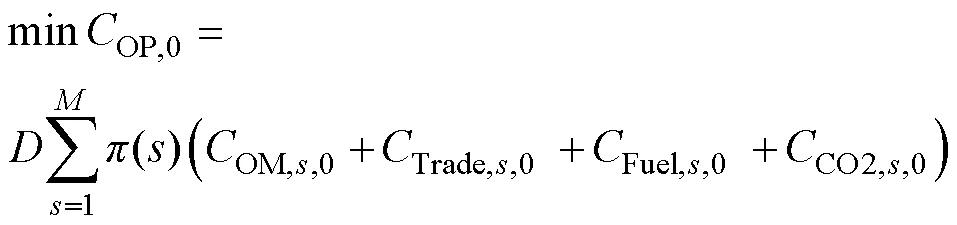
不确定性优化模型的下层目标函数为

（1）设备维护成本

确定性优化的设备维护成本为

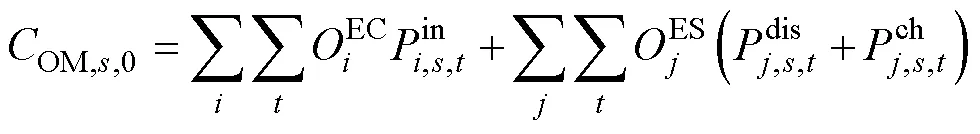
由不确定性因素导致的设备维护成本变化量为

化量。

（2）能源交互成本

确定性优化模型的能源交互成本为

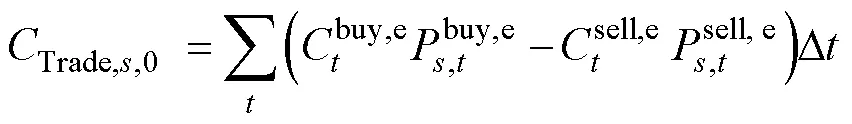
不确定性因素导致的能源交互成本变化量为

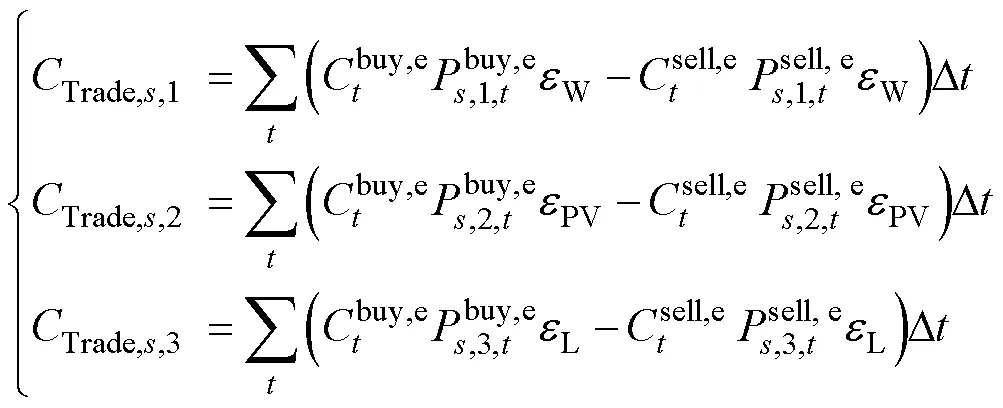
化量。

（3）燃料购买成本

确定性优化模型的燃料购买成本为

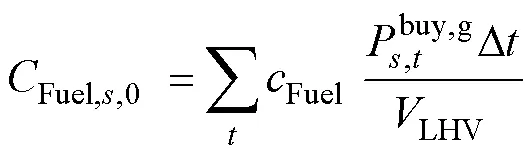
不确定性因素导致的燃料购买成本变化量为

（4）碳排放成本

确定性优化模型的碳排放成本为

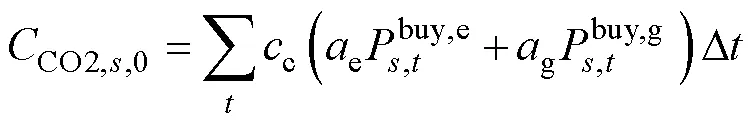
不确定性因素导致的碳排放成本变化量为

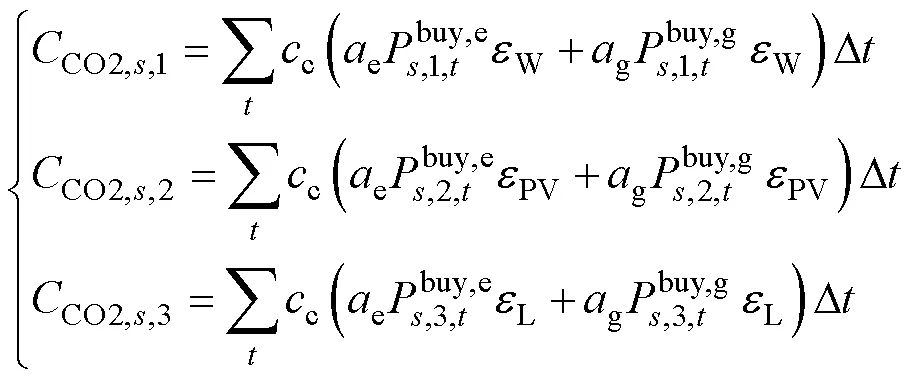
确定性优化模型的约束条件，包含能源功率平衡约束、能源储存设备运行约束、能源交互功率约束等，如式（27）～式（30）所示。其中，风电、光伏、负荷功率仅考虑预测值（仿射中心值），各设备出力为常规数。

（1）能源功率平衡约束

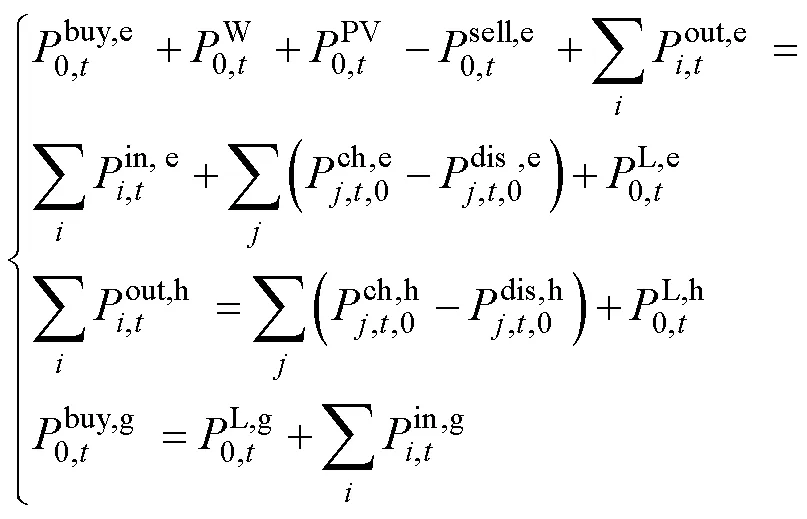
（2）能源储存设备运行约束

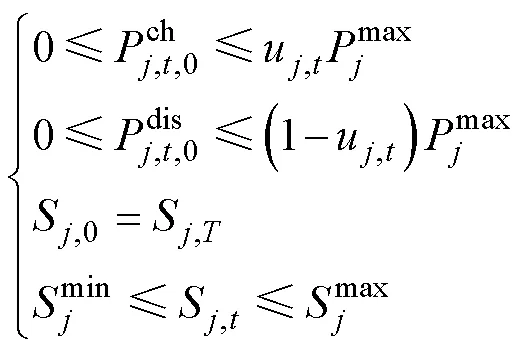
（3）能源转换设备运行约束

（4）能源交互功率约束

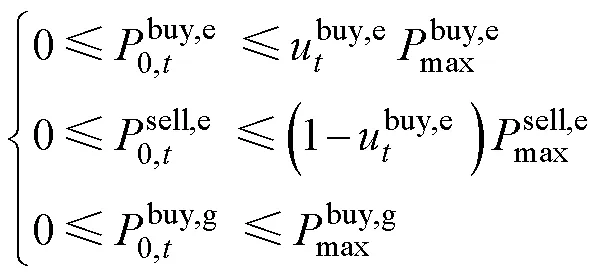
不确定性优化模型的约束条件，如式（31）～式（33）所示。其中，能源存储设备功率及园区与上游能源网络的交互功率均为仿射形式，仿射中心值由确定性优化求得。

（1）能源功率平衡约束

式，其公式类似，如式（8）所示。

（2）能源储存设备运行约束

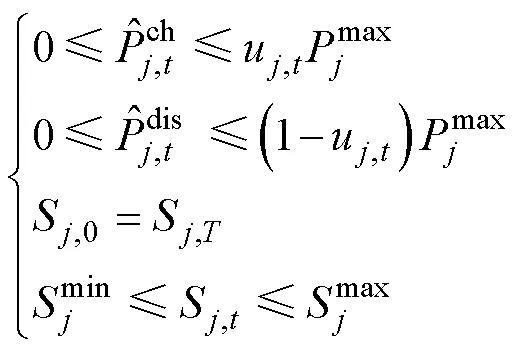
（3）能源交互功率约束

3.3 优化配置模型求解

1）确定性模型求解

上层规划模型决策变量较少，故上层采用遗传算法（genetic algorithm, GA）优化设备类型及台数；下层运行模型为多约束线性模型，采用Cplex求解器求解。上层的容量优化结果作用于下层的目标函数，下层运行优化结果反馈至上层，通过上下层的优化迭代最终求得全局最优解。将求解后的储能设备出力及园区与能源网络的交互功率作为不确定性优化模型对应功率的仿射中心值。

2）不确定性模型求解

在求解过程中，上层采用GA初始化储能设备容量，并传递给下层，下层为考虑源荷预测误差的优化调度模型。由式（5）～式（10）可知，当调整噪声元使运行成本变化最大时，即表示当前噪声元系数下能产生的最大不确定性影响，对应于最恶劣的可能，代表了预测误差导致园区运行成本变化最大的情况。而在最恶劣情况下，可以通过调节噪声元系数，即调整储能设备功率及园区与能源网络的交互功率，以此最小化不确定性因素对运行成本的影响。所以可以将不确定性优化的下层转化为最恶劣情况下（即调整噪声元，max问题）的运行成本最小化问题（即调整噪声元系数，min问题）。下层模型分解后的两个问题如下。

（1）max问题

目标函数为

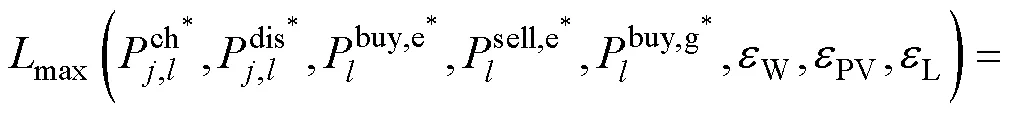
（2）min问题

目标函数为

max问题和min问题模型采用Cplex求解器求解。交替迭代max问题和min问题模型，直到两个模型的年总综合成本相等，则迭代收敛。将下层运行优化结果反馈至上层，通过上下层迭代最终求得全局最优解。优化配置模型的流程如图2所示。

4 算例仿真与分析

4.1 参数设置

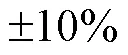
4.2 典型的不确定性研究方法与本文方法对比

以年总综合成本最低为目标进行综合能源系统协同优化配置，系统设备容量配置结果见表1。各类年化成本及设备年平均利用率见表2。其中，场景1为不考虑不确定性的综合能源系统双层协同规划，上层以年化总成本最低为目标求解设备定容问题，下层以设备运行成本最低为目标求解设备调度问题，即文中所介绍的确定性优化。场景2为采用鲁棒优化研究不确定性的综合能源系统双层优化配置，具体模型详见文献[20]。场景3采用本文的方法，将综合能源系统协同规划模型拆分为确定性优化和不确定性优化两个双层规划模型，最后叠加两个模型的求解结果得到总的优化配置方案。其中设备年平均利用率的计算方法为

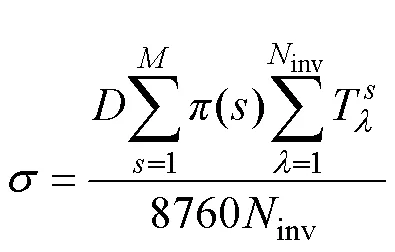
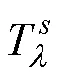
1）由表1和表2可知，比较场景1和场景2，场景2受光伏出力和负荷功率波动影响，年总综合成本有了较为明显的上升，同时由于源荷功率波动，核心设备CHP、EB和GB的配置容量增大。而与场景2相比，场景3的设备配置容量和年总综合成本有所降低，设备利用率有所提高，这说明本文研究的仿射优化方法能在提高配置经济性的同时，降低保守性。对比场景1和场景3，除储热设备容量增加，其余设备配置容量不变，可以验证本文的方法主要是以储电、储热设备应对源荷不确定性，园区设备容量配置结果受不确定性的影响小，经济成本增加，设备利用率提升。

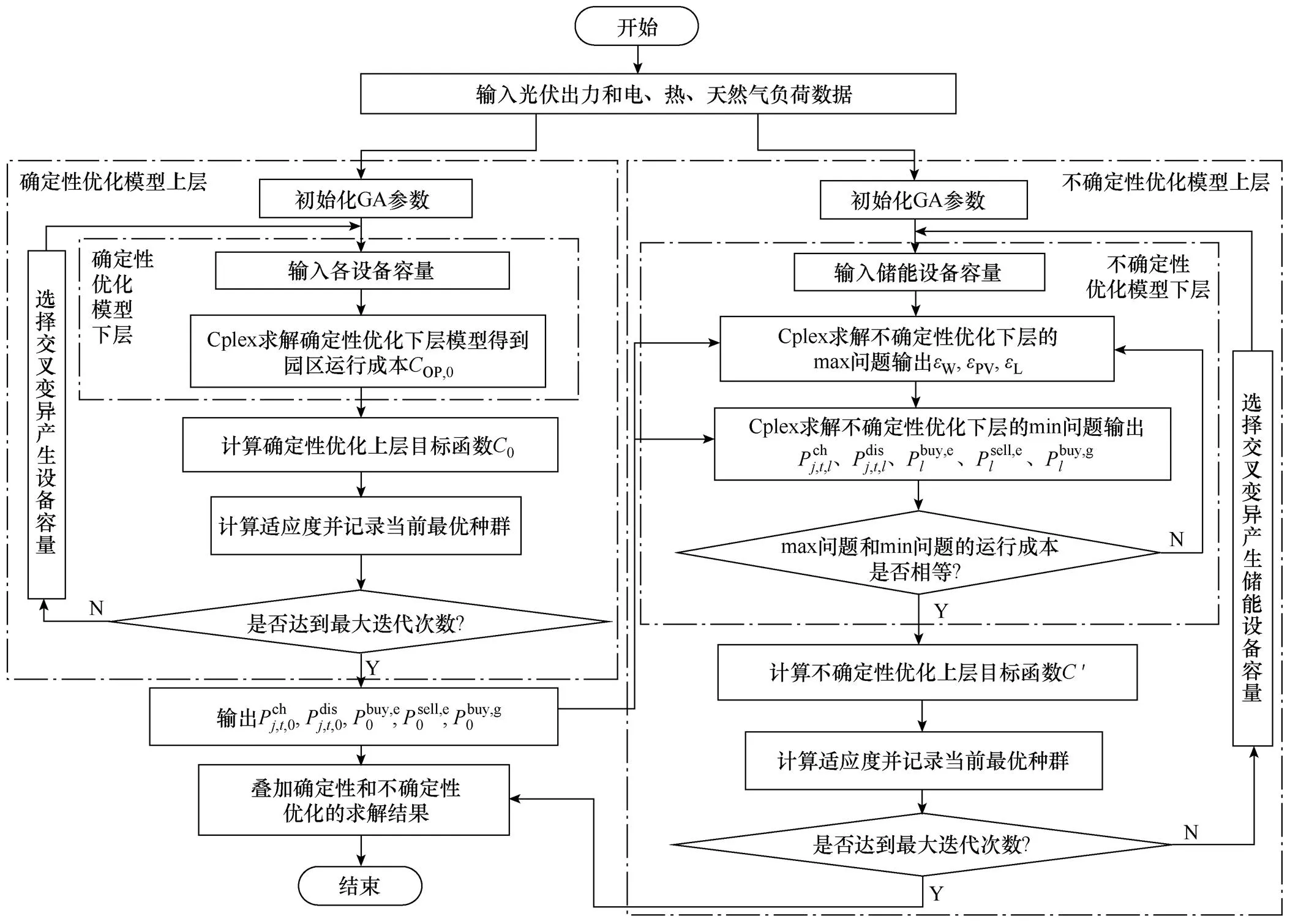
图2 优化配置模型流程

表1 设备容量配置结果

表2 系统各类年化成本及设备年平均利用率

2）由表2可知，场景3较场景2的投资成本下降11.40%，维护成本下降8.17%，购气成本提高8.04%，与电网交互成本提高2.27%，碳排放成本提高2.55%，场景3和场景2均考虑源荷不确定性，场景2增大CHP、EB和GB的配置容量应对源荷的预测误差，所以投资成本和设备维护成本较高。而由于储能设备投资、运行、维护成本较高，场景3主要通过增加与上游能源网络的交互值应对源荷预测误差，所以购气成本与电网交互成本及碳排放成本有所增加。场景3较场景2的年总综合成本下降0.32%，其经济性略优于场景2。场景1的经济性表现最优，主要是因为没有考虑源荷不确定性。

3）由表2可知，场景3在设备年平均利用率上较场景1提高2.57%，较场景2提高0.75%。对于未考虑不确定性的场景1，部分时段的风光出力描述过于理想化，进而导致系统部分设备在出现极限情况时不会投入使用，使系统设备利用率更低。

4.3 仿射优化配置结果分析

图3为场景3下电、气、热功率优化调度的结果。园区购能功率、园区内能量转换设备的输出功率、能源储存设备放能功率为正，园区售能功率、负荷功率、能源转换设备输入功率、能源储存设备储存功率为负。

从图3可以看出，园区电、气负荷需求一般，热负荷需求量较大，由于电价较低，以电制热成为最经济的供热方式，电锅炉为供热的主要设备。由于购买天然气成本较高，热电联产设备仅在电价高峰时满载运行，在电价低谷时，园区购电量很大。气负荷均由园区购气满足。

1）在01:00～07:00和22:00～24:00时段，光伏没有出力，电负荷需求处于当日低谷，热负荷需求处于当日高峰；此时，园区向电网购电以满足电负荷需求且供电给电锅炉。电锅炉平稳出力，由于热负荷依旧存在缺额，园区购气给燃气锅炉确保热功率平衡。

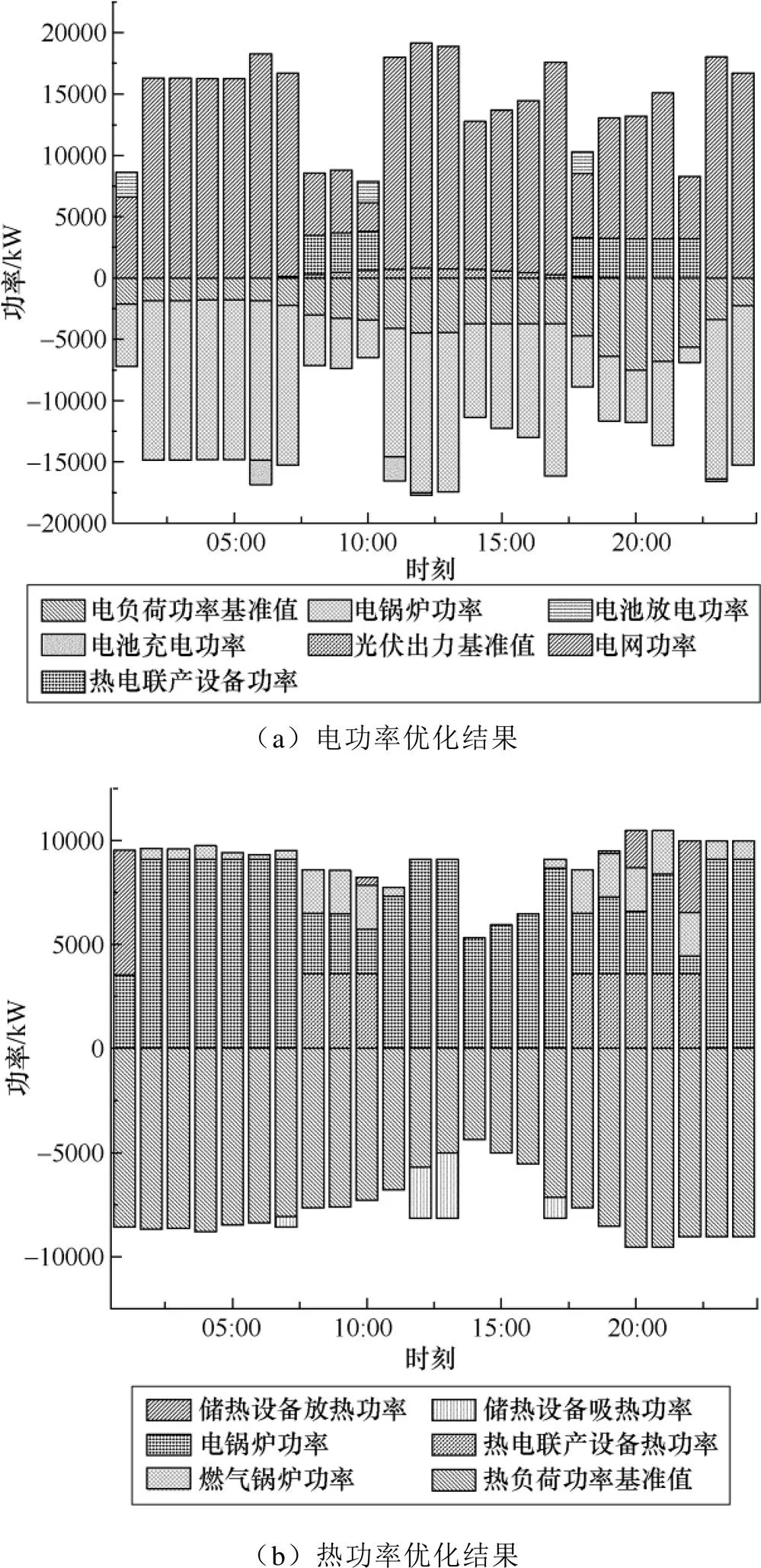
2）在08:00～10:00和18:00～22:00时段，光伏出力很小甚至没有，电负荷处于当日较高水平，热负荷处于当日平值，但需求量依旧较高。电价处于当日峰时段，所以热电联产设备和燃气锅炉运行功率较大，满足电、热负荷需求。电负荷缺额部分由电网和储电设备放电提供，热负荷缺额部分由燃气锅炉供热。

3）在10:00～18:00时段，光伏出力逐渐减小，电负荷处于当日平时段或者谷时段，热负荷处于当日谷时段，园区向电网购电和光伏发电共同确保电功率平衡；热负荷功率由电锅炉提供。

5 结论

本文提出了一种计及源荷不确定性的综合能源系统协同优化配置方案。基于仿射优化理论，将园区优化配置模型拆分成确定性优化和不确定性优化，不确定性优化以确定性优化为基础，交替迭代优化源荷预测误差导致的储能配置容量的变化量，通过对比不同方案的系统容量配置结果，得到以下结论：

1）将园区优化配置模型拆分成确定性优化和不确定性优化，以不确定性导致的年总综合成本最小化为不确定性优化的目标函数，有利于降低预测误差对优化配置方案的影响；在不确定性优化模型中，以运行成本最大化模型预测源荷功率误差，以运行成本最小化模型调整储能设备出力、园区与上游能源网络的交互值，有利于规划结果尽可能满足各种运行情况。

2）用仿射研究综合能源系统的不确定性问题，有利于优化综合能源系统的优化配置，改善优化配置方案因源荷不确定性导致的系统容量配置过于理想化、设备利用率低等问题。下一步工作可研究考虑多能流不确定性的多园区综合能源系统容量配置问题。

[1] 王莉, 吴任博, 潘凯岩, 等. 园区智能综合能源管理运营中心建设探究[J]. 电气技术, 2019, 20(8): 110- 114, 130.

[2] 程思举, 杨建华, 肖达强, 等. 基于多指标评价的清洁能源互补优选策略[J]. 电气技术, 2020, 21(1): 25-30.

[3] 王昀, 谢海鹏, 孙啸天, 等. 计及激励型综合需求响应的电-热综合能源系统日前经济调度[J]. 电工技术学报, 2021, 36(9): 1926-1934.

[4] 姚志力, 王志新. 计及风光不确定性的综合能源系统两层级协同优化配置方法[J]. 电网技术, 2020, 44(12): 4521-4531.

[5] 侯慧, 刘鹏, 黄亮, 等. 考虑不确定性的电-热-氢综合能源系统规划[J]. 电工技术学报, 2021, 36(增刊1): 133-144.

[6] 郭尊, 李庚银, 周明, 等. 考虑网络约束和源荷不确定性的区域综合能源系统两阶段鲁棒优化调度[J].电网技术, 2019, 43(9): 3090-3100.

[7] 苏永新, 聂伟棋, 谭貌. 考虑风电接入和气电转换的综合能源系统日前区间优化[J]. 电力系统自动化, 2019, 43(17): 63-71.

[8] 江泽涛. 含多能源站的电气热综合能源系统区间运行优化和博弈均衡研究[D]. 广州: 华南理工大学, 2019.

[9] 沈欣炜, 郭庆来, 许银亮, 等. 考虑多能负荷不确定性的区域综合能源系统鲁棒规划[J]. 电力系统自动化, 2019, 43(7): 34-41.

[10] 张晓辉, 刘小琰, 钟嘉庆. 考虑奖惩阶梯型碳交易和电-热转移负荷不确定性的综合能源系统规划[J].中国电机工程学报, 2020, 40(19): 6132-6142.

[11] HUANG Guohe, BAETZ B W, PATRY G G. A grey linear programing approach for municipal solid waste management planning under uncertainty[J]. Civil Engineering Systems, 1992, 9(4): 319-335.

[12] 仇知, 王蓓蓓, 贲树俊, 等. 计及不确定性的区域综合能源系统双层优化配置规划模型[J]. 电力自动化设备, 2019, 39(8): 176-185.

[13] 周星球, 郑凌蔚, 杨兰, 等. 考虑多重不确定性的综合能源系统日前优化调度[J]. 电网技术, 2020, 44(7): 2466-2473.

[14] 张聪. 基于区间理论的不确定性无功优化模型及算法[D]. 广州: 华南理工大学, 2018.

[15] 邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(增刊2): 674-683.

[16] 包伟涔, 韦钢, 刘佳, 等. 基于区间模型的多能互补系统优化运行[J]. 电力系统自动化, 2019, 43(11): 8-16.

[17] QUETE D R, CANIZARES C A. An affine arithmetic- based energy management dystem for isolated micro- grids[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 2989-2998.

[18] COMBA J L D, STOLFI J. Affine arithmetic and its applications to computer graphics[C]//Proceedings of VI SIBGRAPI (Brazilian Symposium on Computer Graphics and Image Processing), Brazil, 1990: 9-18．

[19] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.

[20] 林晓明. 园区能源互联网优化运行及能源设备规划研究[D]. 广州: 华南理工大学, 2019.

Optimal allocation of integrated energy system considering the uncertainty of multi-energy flow

GAO Tongtong1,2SHAO Zhenguo1,2CHEN Feixiong1,2

(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108; 2. Fujian Smart Electrical Engineering Technology Research Center, Fuzhou 350108)

The comprehensive energy system has great operation uncertainty. Ignoring this uncertainty in the planning process will lead to the problem of too ideal equipment configuration capacity and low equipment utilization rate. The integrated energy system collaborative planning model is established by using affine variable, and the affine optimization model is decomposed into two subproblems: minimum value target in the center of the affine function and minimum variation of affine function due to the impact of uncertainty factors. The former only considers the source of power load forecast uncertainty optimization model. The latter considers the source load prediction error, and makes the configuration result least affected by uncertain factors by alternating iteration of max model and min model. An example of comprehensive energy system planning in a park is used to verify the effectiveness and economy of the proposed method.

integrated energy system; planning; energy hub; uncertainty; affine optimization

2021-08-16

2021-08-23

高统彤（1997—），女，福建省福州市人，硕士研究生，主要研究方向为综合能源系统优化配置。

福州市科技创新平台项目（2020-PT-143）