基于Matlab的变压器绕组变形频率响应的仿真研究

陈 杰 兰 生 林 野 许明龙 朱志豪

基于Matlab的变压器绕组变形频率响应的仿真研究

陈 杰 兰 生 林 野 许明龙 朱志豪

（福州大学电气工程与自动化学院，福州 350108）

频率响应法（FRA）是检测电力变压器绕组变形的一种可靠方式，本文以三绕组变压器为研究对象，提出考虑各个单元之间互感和绕组相邻线饼间电容的模型。首先，采用有限元软件Maxwell建模求取正常及变形绕组的等效电路参数；其次，根据仿真得到的等效电路参数，在Matlab中建立状态空间模型，通过参数矩阵进行频率响应计算，得出高压绕组轴心偏移和饼间间距变化两种典型绕组变形对频率响应曲线的影响规律。研究结果对后续提取反映频率响应特性的特征向量，实现变压器绕组变形类别的识别具有一定参考价值。

频率响应；有限元；绕组变形；变压器；状态空间方程

0 引言

电力变压器作为电力系统的重要组成部分，是整个系统的命脉所在，其工作状态正常对保障整个电网的安全运行具有重大意义[1]。据相关资料统计，绕组变形是电力变压器发生故障的主要原因[2-3]。变压器绕组的轻微变形不易被发现且具有一定的累积效应[4]，随着变形的加剧，当再次受到短路电流冲击时，可能会造成变压器严重损坏。因此，积极开展对变压器绕组变形的研究十分必要。

频率响应法（frequency response analysis, FRA）是进行变压器绕组变形检测的一种有效方法，其具备试验设备简单、检测灵敏度高、重复性好等优点[5]。国内外的专家和学者针对绕组变形引起频率响应变化的机理进行了大量研究。当前应用最为广泛的方法是建立等效电路模型进行频率响应传递函数的计算，探索绕组变形与频响曲线的关联性。文献[6-7]采用有限元法计算变压器等效电路模型参数，考虑铁心磁导率等对10Hz～10MHz频率范围内变压器绕组的电感和电阻参数的影响，提升了等效电路模型的准确性。文献[8-9]提出改进型的绕组频率响应曲线仿真方法，对各种变形故障程度对变压器等效电路参数的影响进行了探索。文献[10]借助有限元法计算不同变形类别和变形程度下的绕组等效电路参数，并利用电路仿真软件建模探索了等效电路参数变化对频率响应特性曲线的影响。

以上研究均是针对常见的双绕组变压器，本文以三绕组变压器为研究对象，提出考虑各个单元之间互感和绕组相邻线饼间电容的模型，在Matlab中创建状态空间模型，通过参数矩阵进行频率响应计算，重点分析高压绕组轴心偏移和饼间间距变化两种典型绕组变形对频率响应曲线的影响规律。

1 等效电路模型创建与电路参数求取

1.1 变压器绕组的等效电路模型

在进行频率响应测试时，变压器绕组可以等效成由电阻、电感（互感）、电容组成的无源网络，因此可搭建如图1所示的等效电路模型对绕组进行频率响应仿真[11]。对于变压器绕组等效电路模型中的电容、电感等参数，往往采用解析公式法进行计算，但它仅适用于正常绕组，不适用于不规则变形绕组。有限元技术是一种利用微小离散元来模拟求解实际连续域的方法，能够将复杂问题简单化，精确求解不规则物体的电磁特性，弥补解析公式法带来的限制[10]。因此，本文通过有限元软件Maxwell仿真计算绕组的等效电路参数，建立以线饼为单元的连续式绕组分布式模型。对图1所示模型以高压绕组上下两饼为一个单元进行简化，绕组的简化等效电路如图2所示。其中，in为输入电压，i为输入电阻，out为输出电压，o为匹配电阻，为绕组线圈自感，为绕组的自电阻，s为等效纵向电容（包括匝间电容z和饼间电容b），s为电容并联电导，g为对地电容，g为绝缘电导。

图1 绕组等效电路

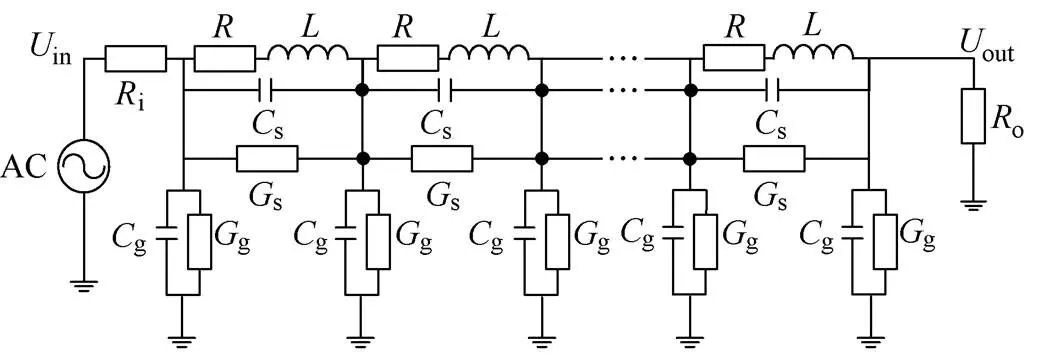
图2 绕组简化等效电路

1.2 基于状态空间方程的频率响应模型

常见的频率响应仿真中，常常是利用电路仿真软件搭建电路模型进行研究，在电路单元较多的情况下，参数的设置与修改将变得繁杂，因此本文提出基于状态空间方程的频率响应模型，通过参数矩阵进行频率响应计算，建立便捷的电路仿真方法，提高计算的速度和精度。

本文搭建7级分布式参数频率响应模型。根据图2所示的简化等效电路，选取各单元的首末端节点电压相量（）和电流相量（）作为状态变量，在Matlab中构建状态空间方程，以获取不同频率下的各个节点的传递函数，进而绘制频率响应曲线[11]。以图3所示的三阶等效电路为例，简述基于状态空间方程的频率响应模型构建过程。

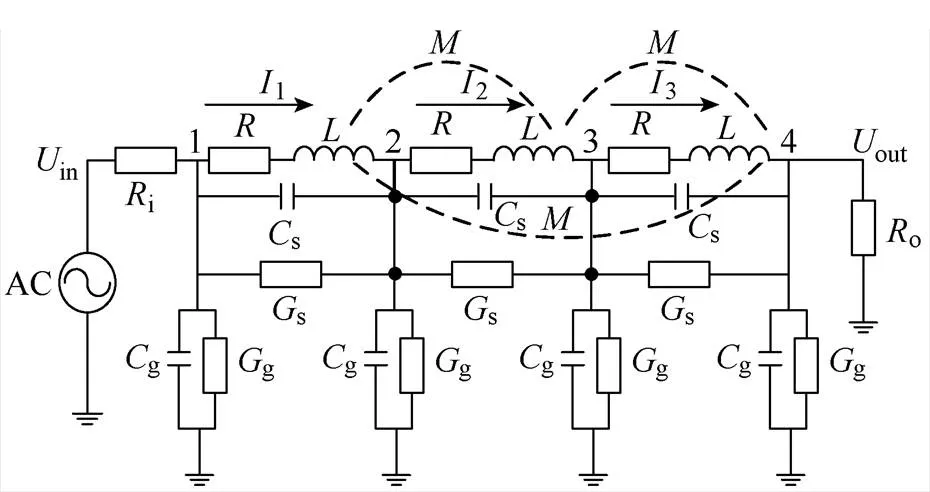
图3 三阶等效电路

图3所示三阶等效电路有4个节点，分别记为1、2、3、4。根据基尔霍夫电压、电流定律，对于节点2有

同理，对于其他节点有类似的电压电流关系，由此可以建立如下矩阵方程，即

假设以节点1作为信号源输入节点，输入电压为1，为了获取传递函数，将1提取出来，对式（2）和式（3）进行移动和变换，并将矩阵方程转换到频域，得

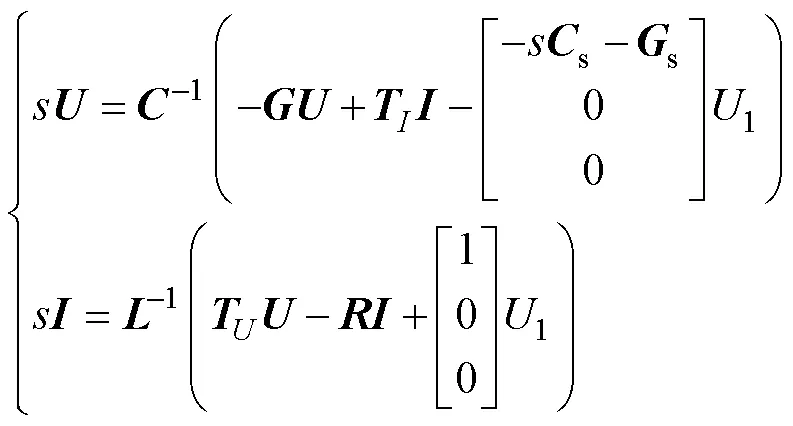
式中：为复频率；为电流系数矩阵；为电流矩阵；为电容矩阵；为电导矩阵；为电压矩阵；为电压系数矩阵；为电感矩阵；为电阻矩阵。

令式（4）中的1的相关系数矩阵分别为1和2，则有

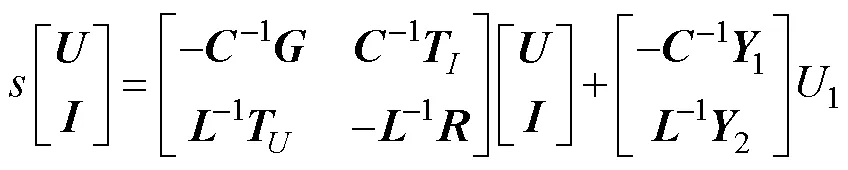
则所有端口的电压及电流与1的比值为

式中，为单位矩阵。

式（6）即为所有节点电压电流与输入节点电压的传递函数矩阵。由此可推广到阶电路，在Matlab中建立状态空间模型，通过参数矩阵进行频率响应计算，绘制得到频率响应曲线。

1.3 基于有限元法的绕组等效电路参数求取

本文以110kV油浸式电力变压器（型号：SSZ11—50000/110）作为研究对象，其实际尺寸参数与绝缘材料参数见表1～表3。根据所列的参数在Maxwell中搭建有限元模型进行电气参数计算[12]，主要包括：匝间与饼间电容、等效纵向电容、等效对地电容、电感（考虑互感）。

表1 变压器的尺寸参数 单位: mm

表2 高压绕组尺寸参数

表3 绝缘材料相对介电常数

1）匝间电容的求取

变压器高压绕组双层线饼模型如图4所示。其中，每层线饼的匝数设置为7匝，为方便求解，将线饼各匝进行编号，上层从外到内依次为Z1～Z7，下层从内到外依次为Z8～Z14。匝绝缘介电常数取3.5，通过在静电场求解器中进行多次静电模拟来计算电容参数矩阵。

图4 高压绕组双层线饼模型

由于线匝的宽度远远小于绕组线圈的平均直径，因此匝间电容可由平板电容公式[13]计算得

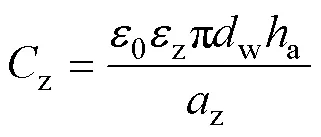
使用解析公式法与有限元法计算部分匝间电容的结果对比见表4。解析公式法和有限元法求得的匝间电容平均值分别为636.05pF、643.19pF。两者的相对误差范围为0.77%～1.42%。

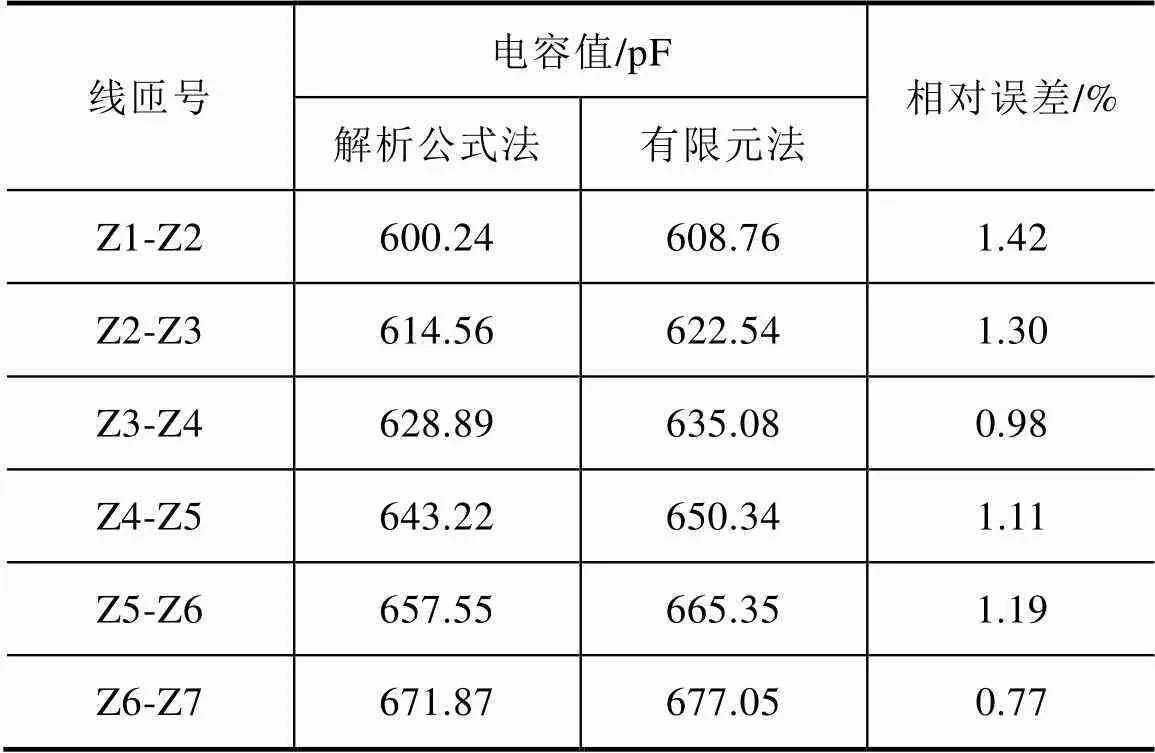
表4 绕组的匝间电容

2）饼间电容的求取

三维线饼模型如图5所示，线饼从上往下依次记为B1～B14。饼间的绝缘等效介电常数取2.46，分别计算高压绕组上下线饼各匝间的电容值，最后求和取得高压绕组各线饼饼间电容值。部分饼间电容计算结果见表5。

图5 三维线饼模型

表5 绕组的饼间电容

由于线匝的宽度远远小于绕组线圈的平均直径，因此饼间电容可由平板电容公式[13]计算得

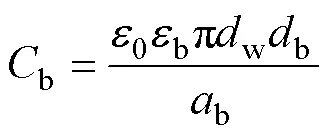
有限元法和解析公式法得到的饼间电容值平均值分别为2 605.86pF、2 589.57pF，相对误差为0.62%。

3）等效纵向电容的求取

等效纵向电容是指线匝之间的匝间电容及线饼之间的饼间电容，二者皆为分布参数，其数值大小由线匝之间或线饼之间的静电储能决定[13]。因此，根据能量相等原理，等效纵向电容的计算公式为

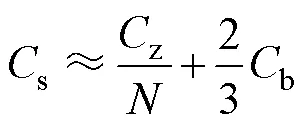
式中：s为等效纵向电容；为线饼匝数。

将得到的绕组匝间电容和饼间电容代入式（9），有限元法和解析公式法计算得到的等效纵向电容值分别为1 829.12pF、1 817.24pF，相对误差为0.65%。

4）等效对地电容的求取

等效对地电容的仿真模型如图6所示。在模型中设置油箱、中压绕组、低压绕组和铁心部分为接地零电位，求解得到单个高压绕组线饼的对地电容值见表6。

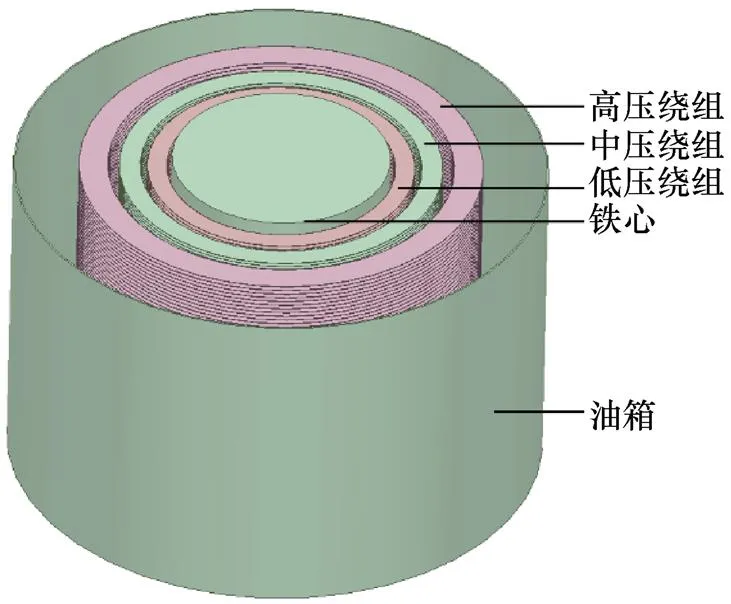
图6 等效对地电容的仿真模型

表6 单个高压绕组线饼的对地电容值

5）电感及互感的求取

通常情况下，在高于1kHz的高频输入源作用下，变压器铁心的磁导率几乎可以视为空气磁导率。因此，本文忽略铁心影响，建立空心线圈模型以求解电感参数，模型如图5所示。将高压绕组线饼分别编号为H1～H14，每饼匝数为7匝，设置求解域，施加1A电流源于每饼线圈的横切面，在静磁场中求解得到电感矩阵。部分电感参数值见表7。其中，对角线部分为线圈自感，非对角线部分为各线圈之间的互感。

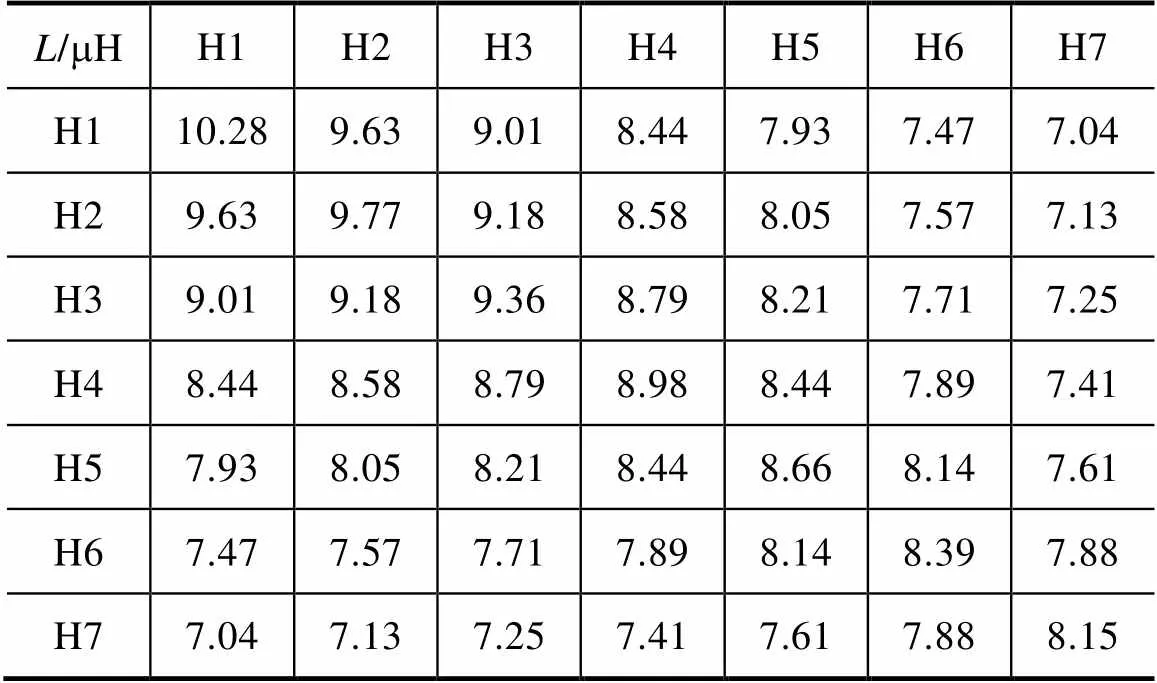
表7 电感参数

2 绕组变形后的频率响应特性分析

当绕组结构发生改变时，等效电路中对应的电气参数数值也会随之发生变化，进而导致谐振点对应的频率位置与幅值大小发生改变。为了研究不同电路参数变化对频率响应曲线的影响规律，本文依据上述仿真模型求取绕组不同变形类型的电路参数，在Matlab中搭建频率响应模型，重点分析高压绕组轴心偏移和饼间间距变化两种典型绕组变形对频响曲线的影响规律。

2.1 绕组轴心偏移

在Maxwell中搭建绕组轴心偏移模型，在模型中共设置7个偏移量，范围为5～35mm，以此来模拟不同程度的轴心偏移。通过对正常绕组和高压绕组不同程度的轴心偏移进行仿真发现，等效电路中的电感和等效纵向电容参数几乎没有发生变化，变化量最大的是对地电容，尤其高中压绕组间电容的变化量最大。高压绕组轴心偏移量与对地电容值变化关系如图7所示。由图7可知，随着轴心偏移程度的增大，对地电容值增大，并且轴心偏移程度越大，对地电容值的变化量越大。

图7 高压绕组轴心偏移量与对地电容值变化关系

对高压绕组轴心偏移30mm和正常绕组两种情况进行分析，对地电容变化情况见表8。从高压绕组发生轴心偏移后对地总电容与未变形前相比较来看，增加了18.13pF。其中高中压绕组间的电容变化最大，占对地电容总变化量的96%。

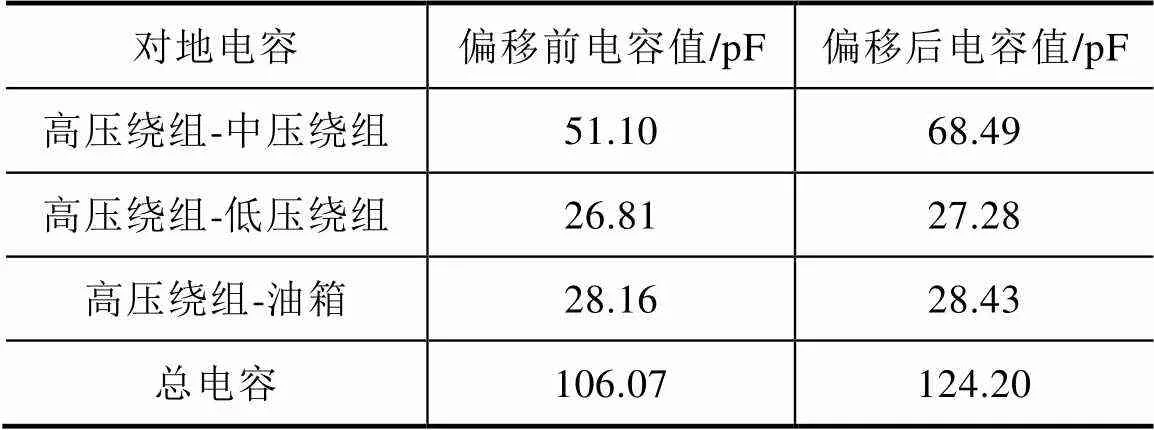
表8 高压绕组轴心偏移30mm时对地电容变化情况

选取绕组发生轴心偏移25mm、35mm两种情况与正常情况下的频响曲线作对比，研究高压绕组轴心偏移量对频响曲线的影响，如图8所示。

由图8可知，高压绕组发生轴心偏移时，在低于10kHz的频率范围内，几乎观察不到故障对频率响应曲线的影响。在10～600kHz的频率范围内，频率响应曲线明显左移，谐振点的频率减小；随着轴心偏移程度增大，频率响应曲线的谐振点相对正常绕组呈现更加明显的左移现象。在600～1 000kHz的频率范围内，频率响应曲线幅值比正常情况要稍微低一些。

对高压绕组轴心偏移情况作进一步解析，依照标准DL/T 911—2016中所列出的公式，计算相关系数作为参考。不同轴心偏移量下的相关系数见表9，其中LF为曲线在低频段（1～100kHz）的相关系数，MF为曲线在中频段（100～600kHz）的相关系数，HF为曲线在高频段（600kHz～1MHz）的相关系 数[14]。

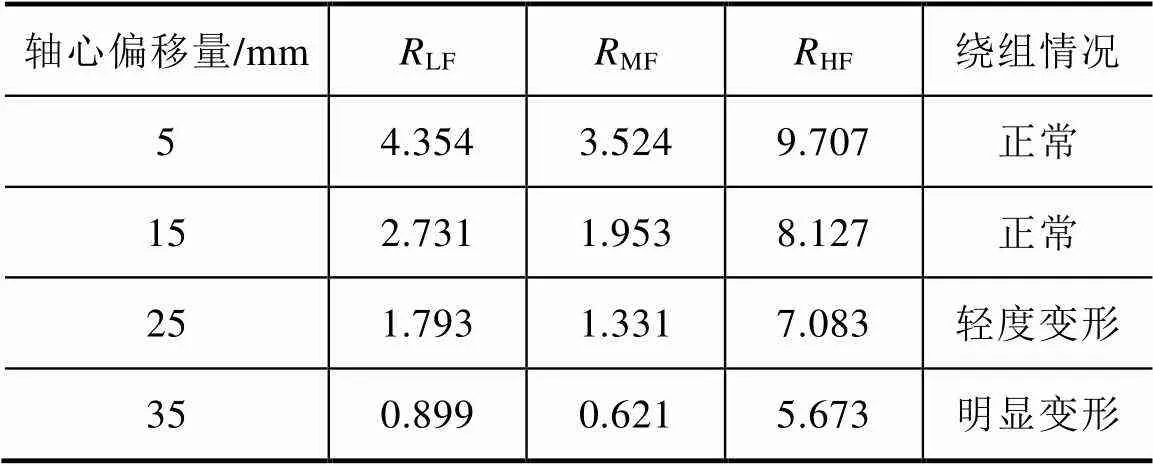
表9 不同轴心偏移量下的相关系数

由表9中数据可知，绕组发生轴心偏移时，当轴心偏移量较小（5～15mm）时，各频段相关系数均在正常指标范围。随着偏移量的增加，各频段相关系数呈现减小的趋势，曲线相关性变差，尤其低频段的相关系数减小到超出了正常指标，可以初步判断绕组发生较为明显的变形。

在本文所研究的变压器中，正常高压绕组的饼间间距为3mm。在Maxwell中建立高压绕组饼间间距变化模型，在模型中分别设置3个单元饼间间距减小为2.7mm、2.4mm、2.1mm。在仿真中发现，饼间间距改变后，等效电路中的电感、对地电容参数值的变化微乎其微，而等效纵向电容是其中变化最大的，这主要是由饼间电容的变化引起的。高压绕组饼间间距改变后的饼间电容、等效纵向电容变化如图9所示。由图9可知，随着饼间间距减小，饼间电容增大，等效纵向电容随之增大。

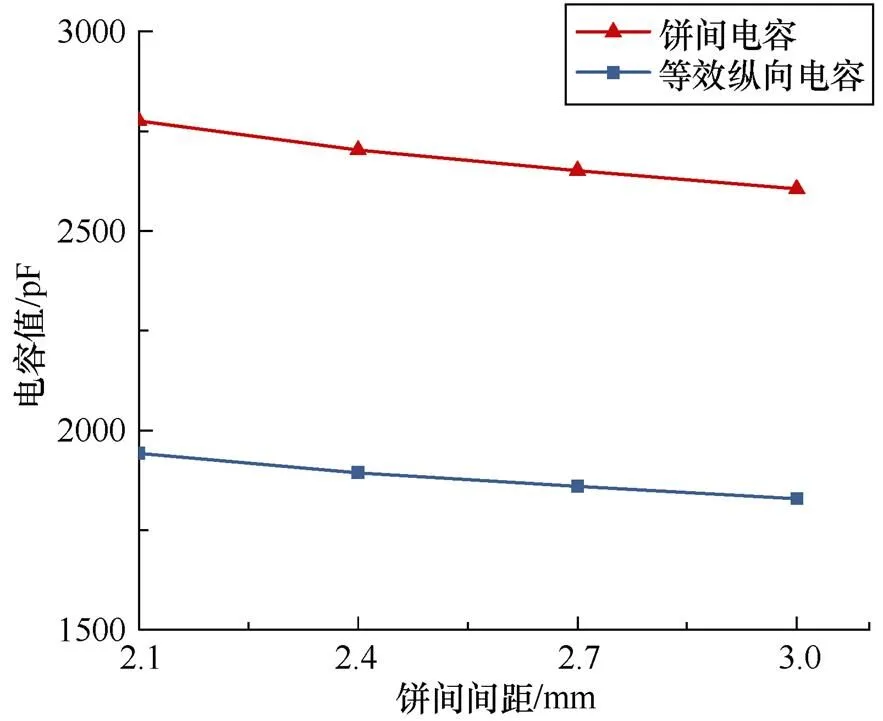
图9 饼间间距改变后饼间电容、等效纵向电容变化

2.2 绕组饼间间距变化

选取高压绕组3个单元饼间间距分别为2.4mm、2.1mm的情况与正常绕组的频率响应曲线作对比，研究绕组饼间间距变化对频率响应曲线的影响，如图10所示。

由图10可知，高压绕组饼间间距减小，谐振波峰、波谷的频率也相应减小。在低于50kHz的频率范围内，频响曲线与正常情况时几乎一致。在50～600kHz的频率范围内，频响曲线明显左移，谐振点的频率稍微减小。随着饼间间距减小得越多，频响曲线中的谐振点相对正常绕组呈现越明显的左移现象。在600～1 000kHz的频率范围内，频率响应曲线整体幅值相较正常情况要稍微高一些。

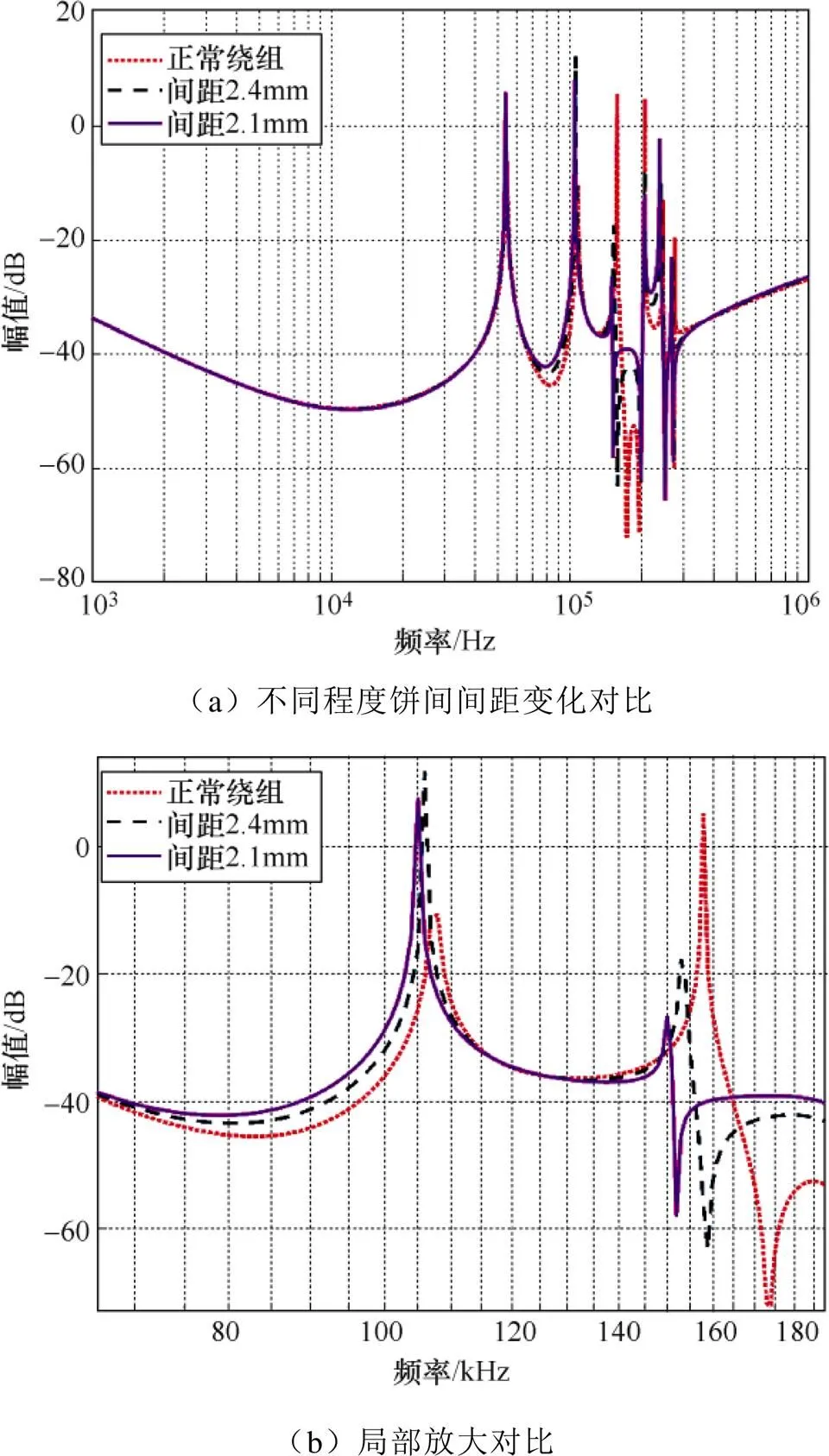
图10 绕组饼间间距变化对频率响应曲线的影响

依照标准DL/T 911—2016中所列出的计算方法，计算相关系数作为参考，进一步分析高压绕组的饼间间距改变的情况。不同饼间间距下的相关系数见表10。

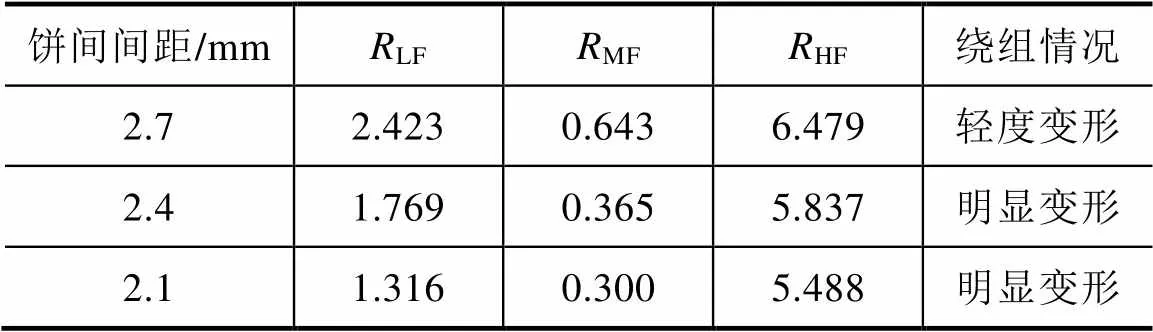
表10 不同饼间间距下的相关系数

由表10中数据可知，当高压绕组的3个单元饼间间距减小时，各频段相关系数减小，依照相关系数可以初步判断出绕组已经发生轻度变形。随着饼间间距进一步减小为2.4mm和2.1mm时，各频段相关系数呈现减小的趋势更明显，曲线相关性变差，根据中频段的相关系数减小，可以判断出绕组已经发生较为明显的变形。

3 结论

本文根据三绕组变压器的相关参数，借助有限元软件进行了建模仿真，获取了正常及变形绕组的等效电路参数的相关数据。按照变压器实际结构所搭建的模型进行计算，所得到的电气参数结果较解析公式法精度要高。

在Matlab中搭建了基于状态空间方程的频率响应分析模型，对高压绕组发生轴心偏移和饼间间距改变两种典型变形进行了仿真分析，得到了两种典型的绕组变形对频率响应曲线的影响规律。

电力变压器绕组结构发生改变后，其频响曲线会发生相应的变化。可提取频率响应曲线在整个频率范围内的变化特性作为检测绕组变形的指标，实现对变压器绕组变形类型的进一步识别。

[1] 孙翔, 何文林, 詹江杨, 等. 电力变压器绕组变形检测与诊断技术的现状与发展[J]. 高电压技术, 2016, 42(4): 1207-1220.

[2] 张云, 李少逸, 黄晓波. 一起220kV变压器突发短路故障分析[J]. 电气技术, 2018, 19(5): 94-98.

[3] 刘云鹏, 李欢, 田源, 等. 基于分布式光纤传感的绕组变形程度检测[J]. 电工技术学报, 2021, 36(7): 1347-1355.

[4] 杜国安, 徐玉珍, 兰生, 等. 基于磁-结构场耦合的变压器绕组变形的因素分析[J]. 电气技术, 2021, 22(1): 1-7, 46.

[5] 张秀斌, 吕景顺, 温定筠, 等. 基于频率响应法的110kV主变压器绕组变形案例分析[J]. 电气技术, 2015, 16(4): 97-100.

[6] ABEYWICKRAMA N, SERDYUK Y V, GUBANSKI S M. High-frequency modeling of power transformers for use in frequency response analysis (FRA)[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2042- 2049.

[7] HASHEMNIA N, ABU-SIADA A, ISLAM S. Improved power transformer winding fault detection using FRA diagnostics-part 1: axial displacement simulation[J]. IEEE Transactions on Dielectrics and Electrical Insu- lation, 2015, 22(1): 556-563.

[8] HASHEMNIA N, ABU-SIADA A, ISLAM S. Improved power transformer winding fault detection using FRA diagnostics-part 2: radial deformation simulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 564-570.

[9] ABEYWICKRAMA K G N B, PODOLTSEV A D, SERDYUK Y V, et al. Computation of parameters of power transformer windings for use in frequency response analysis[J]. IEEE Transactions on Magnetics, 2007, 43(5): 1983-1990.

[10] 邹林, 廖一帆, 罗兵, 等. 基于有限元法探究电力变压器绕组变形频率响应的仿真研究[J]. 电力自动化设备, 2017, 37(1): 204-211.

[11] 江俊飞, 周利军, 李威, 等. 自耦变压器分裂式绕组频率响应分析建模与故障绕组识别[J]. 中国电机工程学报, 2018, 38(10): 3102-3108.

[12] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.

[13] 刘传彝. 电力变压器设计计算方法与实践[M]. 沈阳: 辽宁科学技术出版社, 2002.

[14] 电力变压器绕组变形的频率响应分析法: DL/T 911—2016[S]. 北京: 中国电力出版社, 2016.

Simulation research on frequency response of transformer winding deformation base on Matlab

CHEN Jie LAN Sheng LIN Ye XU Minglong ZHU Zhihao

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108)

Frequency response analysis (FRA) is one of the main methods to detect the winding deformation of power transformer. This paper takes the three-winding transformer as the research object and proposes a model that considers the mutual inductance between each unit and the capacitance between the adjacent windings. Firstly, the equivalent circuit parameters of normal and deformed windings are calculated through the simulation of finite element software Ansys Maxwell. Secondly, according to the equivalent circuit obtained by the simulation, the state space model is established in Matlab. The frequency response is calculated through the parameter matrix, and the influence of two typical winding deformation types of the axis deviation of the high voltage winding and the change of the gap between the disks offset is obtained. The research results have a certain reference value for extracting the feature vector reflecting the frequency response characteristics and realizing the identification of transformer winding deformation type.

frequency response; finite element; winding deformation; transformer; state space equation

2021-09-30

2021-10-28

陈 杰（1992—），男，福建省莆田市人，硕士研究生，主要从事变压器绕组变形研究。