具有奇异振荡的三维非自治线性Kelvin-Voigt-Brinkman-Forchheimer方程的一些估计

谭青维，朱朝生

西南大学 数学与统计学院，重庆 400715

令Ω⊂R3是一个边界光滑的有界域．本文主要研究Ω上具有奇异振荡力的三维非自治Kelvin-Voigt-Brinkman-Forchheimer方程[1-4]：

(1)

其中：a∈R，b>0，r∈[1，∞)，μ>0是流体的运动粘度，α是流体弹性的表征参数，函数u=u(x，t)=(u1(x，t)，u2(x，t)，u3(x，t))表示流体的速度，p=p(x，t)表示压力．当a，b=0时，方程(1)为带奇异振荡力的Navier-Stokes-Voigt方程[5-10]；当α=0时，方程(1)为带奇异振荡力的Brinkman-Forchheimer方程[11-15]；当a，b，α=0时，方程(1)为带奇异振荡力的Navier-Stokes方程[16-17]．

结合方程(1)，我们考虑如下平均Kelvin-Voigt-Brinkman-Forchheimer方程：

记函数

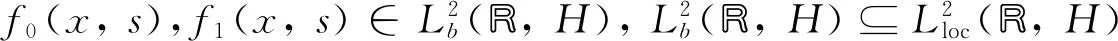
其中常数M0，M1≥0，定义

综上有

引入函数空间

这里clXS表示S在空间X的闭包，H与V是可分的Hilbert空间．令H′是H的对偶空间，V′是V的对偶空间，有VH=H′V′，其中嵌入都是连续且稠密的．H与V分别具有如下内积和范数：

用〈·，·〉表示V′与V之间的对偶集，用|·|p表示Lp(Ω)空间中的范数，用‖·‖E表示巴纳赫空间E中的范数．字母C为常数．

方程(1)的前两个等式，可以写成如下抽象形式

(2)

令A=-PΔ是Stokes算子，P是从L2(Ω)到H的Leray正交投影，有

〈Au，v〉=((u，v))F(u)=P(au+b|u|r-1u)

〈B(u，v)，w〉=b(u，v，w)B(u)=b(u，u)

这里

对于方程(2)的全局解的存在唯一性，可由文献[2]中的标准方法得到如下定理1．

u∈C([τ，T]；V)∩L2(τ，T；V)∩L∞(τ，T；V)∩Lr+1(τ，T；Lr+1(Ω))

我们将考虑具有与时间相关的外力驱动的非自治辅助线性方程，对其进行一系列估计．

Yt(t)+μAY(t)+α2AYt(t)+aY(t)=K(t)，Y(t)|t=τ=0

(3)

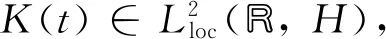
Y(t)∈C([τ，T]；V)∩L2(τ，T；V)，Yt(t)∈L2(τ，T；V′)

且满足不等式

证用Galerkin逼近法，可以推出解的存在，将方程(3)与AY(t)作内积，可得

(4)

由不等式(4)可得

即有

(5)

对不等式(5)在[τ，t]上积分，得

易得

将方程(3)与Y(t)作内积，可得

即

(6)

对不等式(6)在[t，t+1]上积分，再运用Poincaré不等式得

即有

定理2证毕．

(7)

则带奇异振荡力的线性方程

(8)

的解X(t)满足不等式

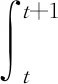
(9)

其中C与K(t)无关．

证首先记

则由(7)式可推出

由积分中值定理和定理2可得

现令

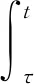
由X(τ)=0，得

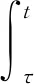
方程(8)在[τ，t]上积分可得

Yt(t)+μAY(t)+α2AYt(t)+aY(t)=Kε(t)，Y(t)|t=τ=0

综上所述可得

所以

‖X(t)‖≤C(|X(t)|2+α2|AX(t)|2)≤Clε

(10)

由不等式(10)可得不等式(9)成立，定理3证毕．