室内环境下基于UWB的TDOA/AOA三维混合定位算法

陆冰琳

（广东东软学院 信息管理与工程学院，广东 佛山 528225）

0 引言

超宽带（UWB）作为一种新兴的无线通信技术，在无需载波的前提下，可直接产生纳米级以下的窄脉冲激励天线，具有低功耗、抗干扰能力强、穿透性强等特点。与ZigBee、RFID、WiFi等室内定位技术相比，UWB技术最大的优势在于其定位精度极高，最低可达厘米级[1]。本文研究重点在于利用UWB技术在室内环境下实现高精度定位。UWB基本定位算法包括：测量信号的到达时间（TOA，Time of Arrival）、到达时间差（TDOA，Difference of Time Arrival）、波达角度（AOA，Angel of arrival）及接受信号强度（RSSI，Received Signal Strength）。其中TOA和TDOA定位算法利用了UWB信号较高的时间分辨率，在实际应用中最为广泛。文献中使用了基于泰勒级数展开的TOA算法，泰勒级数展开法的优点在于求解精度高、稳定性强。然而值得注意的是，算法中若初值估计误差过大，会导致定位精度急剧下降，甚至迭代运算无法收敛。文献提出了使用TDOA/AOA联合定位方案，TDOA算法与TOA算法相比，只需要参考节点间保持时间同步，降低了硬件成本，增加了实用性。同时增加角度信息，使精度有所提高。结论显示，算法在NLOS传播下的误差明显大于LOS传播。在AOA估计过程中，一般采用传统的波速赋形技术。而文献采用二元天线，利用几何原理，通过天线间的TDOA信息得到到达角估计值，降低了复杂度且定位精度极高。然而此算法使用的S-V模型，并未考虑NLOS传播情况。文献结合Chan算法提出了TDOA/AOA混合定位算法，在室内环境中，TDOA误差并非服从理想高斯分布，在NLOS传播中误差会上升。

本文对比以上定位算法的特点，提出基于泰勒级数的TDOA/AOA混合算法。首先利用Wylie鉴别算法分辨参考节点与目标节点间的LOS和NLOS传播，在一定范围内降低了NLOS传播导致的估计距离的误差。通过统计得到LOS和NLOS传播的平均时延值后，对到达距离差进行重构，得到较为准确的初值估计，以此保障之后的算法收敛。同时，依据距离测量标准差，选出可靠性最高的参考节点，对其与目标节点的方位角和俯仰角信息进行估算，作为辅助定位信息。最后结合初值估计结果及角度信息，进行TDOA/AOA混合算法计算，经过迭代后，可得到较为准确的目标节点三维坐标[2]。

1 UWB信号模型

选用PPM-TH-UWB信号作为发射信号，相应的UWB信号发射链路描述如图1：

图1 UWB 发射机模块

2 TDOA/AOA混合定位算法

2.1 Wylie鉴别算法

考虑到在室内环境同时包含LOS和NLOS传播，而NLOS传播方式所导致的误差是干扰定位精度的关键因素之一，因此将使用Wylie鉴别算法减轻NLOS传播的影响[3]。假设每个参考节点与目标节点间的距离测量结果通过多项式拟合来进行平滑处理，即

由于样本的测量误差，除了来自标准测量的误差外，主要由NLOS传播产生。所以，所得样本标准差 越大，所受NLOS影响越大。此时在选出目标节点与LOS传播的参考节点的基础上，选择样本标准差 较小的参考节点作为TDOA/AOA混合算法的参考节点，以此提高定位精度。

2.2 更新距离差

2.3 初值估计

2.4 三维角度估计

为进一步降低定位误差，需要得到角度估计值作为辅助信息，用于之后TDOA/AOA混合算法的计算。此处同样选择可靠度最高的参考节点 ，估计其与目标节点的方位角和俯仰角。

2.4.1 俯仰角估计

如图2所示，假设三维空间中目标节点坐标为(x,y,z)，参考节点 的坐标为，目标节点与参考节点间的距离为，俯仰角为，方位角为。

图2 基于距离和到达角测量的三维空间定位

2.4.2 方位角估计

如图3所示天线阵列：如果信源与阵列的距离远大于阵元的间距，就可假设发射信号入射到天线阵列的时候均为平行的。

图3 角度计算原理

2.5 基于泰勒级数的TDOA/AOA混合算法

假设目标节点与参考节点 的距离为：

更新矩阵B和G后，对式（31）重新进行计算，使估计值不断逼近目标节点的精确位置，当h、k、w减小到一定程度时，最终跳出循环，得到即为所求目标节点的最终估计值。

3 仿真及性能分析

假设选定IEEE802.15.4a信道模型中的室内住宅环境作为仿真背景，通过计算不同定位算法在不同参考节点数量及信噪比条件下的均方根误差（RMSE），对算法的二维及三维定位性能进行评估。

3.1 二维仿真分析

3.1.1 不同参考节点个数

在二维定位算法中，假设信噪比为-5dB，分别选取参考节点为4到9个的条件下，使用TOA定位算法、基于LSE的TDOA定位算法、基于Chan的TDOA定位算法及TDOA/AOA混合算法进行比较，得到的仿真结果如图4所示，各定位算法在选取不同数量的参考节点时，随着参考节点数量的增加，均方根误差均有所下降。然而，由于NLOS传播的存在导致估计距离误差较大，冗余项增加[4]。

图4 不同参考节点下的误差

并不能很好地抵消多径效应产生的时延影响，其中TOA定位算法定位误差最大。基于LSE和基于Chan的TDOA定位算法利用到达时间差，消除了发射及接收机内部的无线时延，定位精度与TOA算法相比有所提高。TDOA/AOA混合算法利用了Wylie鉴别算法在一定程度上减轻了NLOS的影响，使得其对应的均方根误差较小，定位精度更为准确。由于TDOA/AOA混合算法优先选取可靠性较高的参考节点，所以当增加过多的参考节点时可能会引入误差较大的距离估计值，对混合算法定位精度的提高并不明显。

3.1.2 不同信噪比

各定位算法在不同信噪比情况下进行仿真的结果如图5所示，可见随着信噪比的增加，UWB信号受NLOS传播影响逐渐下降，使得各算法在高信噪比条件下的定位精度均有上升。基于Chan的TDOA定位算法中测量误差并非服从零均值高斯分布，使得算法性能下降，其均方根误差大于LSE定位算法；AOA定位算法和基于LSE的TDOA算法在LOS条件下与TDOA/AOA混合算法的定位精度较为接近，然而随着信噪比下降，这两种算法的误差也随之增大。而在NLOS条件下，TDOA/AOA混合算法基于Wylie鉴别算法对NLOS参考节点的筛选及估计距离值的更新，使得混合算法在信噪比较低的条件下，依然保持了较高的定位精度，明显优于其他定位算法。

图5 不同信噪比下的误差

3.2 三维仿真分析

假设选定室内住宅环境作为仿真背景，信噪比为-5dB，参考节点为6个。对基于LSE的TDOA算法、基于Chan的TDOA算法、TDOA/AOA混合算法分别进行500次仿真。

如图6所示，基于LSE的TDOA算法在z轴方向产生的误差波动幅度明显大于x、y轴，使得其整体定位误差急剧增大。

图6 LSE TDOA 三维方向观测误差

如图7所示，与基于LSE的TDOA算法相比，基于Chan的TDOA算法在z轴方向产生的误差波动较前者有所下降，但误差波动幅度仍然大于在x、y轴方向的误差。

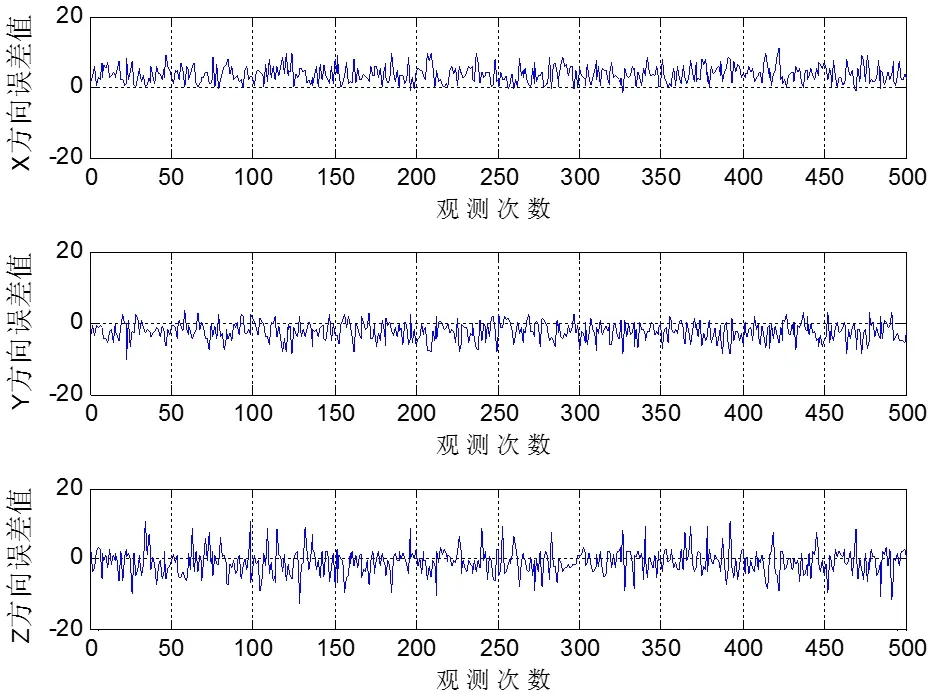
图7 Chan TDOA 三维方向观测误差

如图8可知，TDOA/AOA混合定位算法在x、y方向上的误差均与二维情况下相近，与前两种算法相比，混合算法在z方向上的误差最小，使得整体定位精度依然较高。

图8 TDOA/AOA 三维方向观测误差

如图9所示，由于增加了z方向上的误差，基于LSE的TDOA算法在信噪比较小的情况下误差加剧，此时基于Chan的TDOA算法整体均方根误差优于LSE算法，但在信噪比增大的情况下，LSE误差下降速度明显优于Chan算法。与基于LSE和基于Chan的TDOA算法与相比，TDOA/AOA混合算法均方根误差依然最小。在混合算法中，z方向上的误差是导致均方根误差上升的主要原因。在实际应用中，主要通过z值大致判断人员所在的楼层位置，在楼层位置确定后，依据x、y值判断消防员所在的室内平面位置，可达到较高的定位精度[5]。

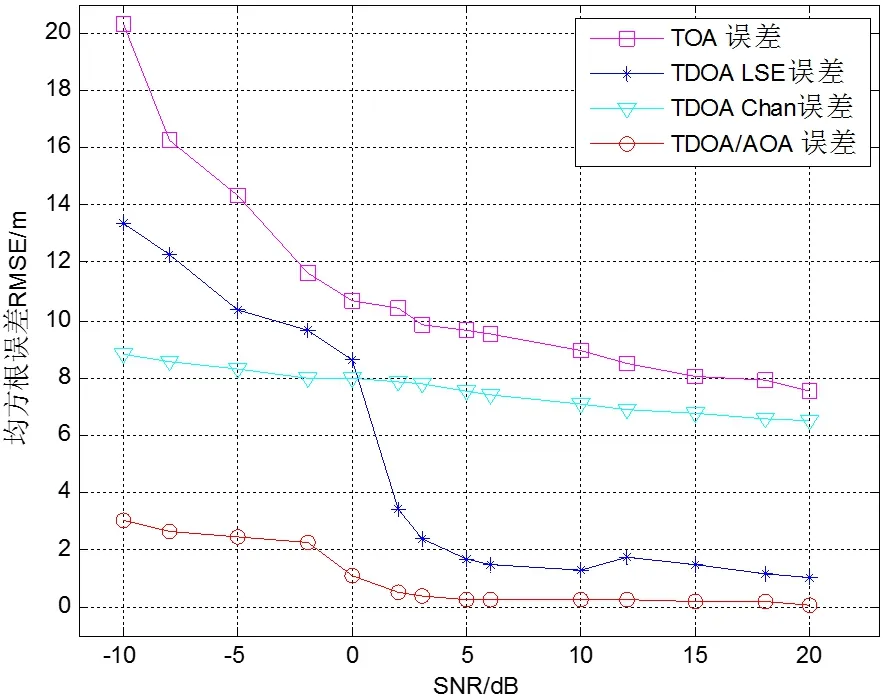
图9 各定位算法不同信噪比下误差值

4 结语

由于室内环境中，存在众多障碍物导致多径效应严重，所以首先利用Wylie鉴别算法判断目标节点与参考节点的LOS和NLOS传播。筛选性能更为优异的参考节点，修正目标节点与参考节点间的到达时间差，选出可靠度最高的参考节点计算其与目标节点的方向角和俯仰角。代入基于泰勒级数的TDOA/AOA混合算法中，进而得到定位精度较高的估计位置。最后利用Matlab软件对各类定位算法进行性能仿真，对比其在不同信噪比条件下的均方根误差，可以得出在各类情况下混合算法的定位精度更为优异。