考虑动载扰动作用的窄煤柱巷道底板失稳机制
2022-03-26赵洪宝刘一洪刘绍强张嘉澔
赵洪宝,刘一洪,刘绍强,张嘉澔,吴 桐
(1.中国矿业大学(北京) 能源与矿业学院,北京 100083;2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001)
0 引 言
在我国井工矿开采中,相当比例矿区采用留设宽煤柱的方式保护回采巷道,由于煤柱很难进行二次回收,导致煤炭资源损失量较大,可达到全矿煤炭损失量的40%[1-2]。 通过沿空留巷或沿空掘巷可有效解决资源浪费的问题,沿空留巷经历了上区段和本区段工作面的两次回采扰动,其稳定性维护较为困难。 沿空掘巷或窄煤柱巷道将巷道布设在采空区边缘,可避开上区段工作面的剧烈扰动,巷道稳定性稍好,在综放工作面中应用较为广泛[3-5]。 随着矿井逐步进入深部开采阶段,地应力增高,巷道受采动影响愈加强烈。 回采巷道底鼓一直是巷道稳定维护的棘手问题,巷道底鼓发生几率随埋深增加而增加,埋深接近1 000 m 时,底鼓发生几率高达80%[6]。
国内外学者针对巷道底板稳定性问题做了较为详尽的研究,取得了丰硕成果。 姜耀东等[7]将底鼓分为了挠曲褶皱、挤压流动、剪切错动和遇水膨胀4种类型;王卫军等[8]认为水平应力对沿空巷道底板的影响较小,巷道底鼓受实体煤底板的高应力挤压影响较大,并提出了加固帮角和窄煤柱的控制技术;候朝炯[9]认为巷道两帮下沉并且底角破坏后,在水平应力的挤压作用下巷道浅部底板鼓起,从而提出了加固巷道帮角和底板的控制原则;杨仁树[10]认为顶板关键岩块的回转变形是巷道非对称底鼓的主要因素,并提出了底板注浆联合锚索支护的底鼓防治方法; 江东海等[11]通过数值模拟发现底板倒棱锥块体的非均匀分布是巷道非对称底鼓的主要原因,基于此提出了反底拱联合预应力锚索的控制对策;文献[12-13]提出了“双壳”治理底鼓技术并对其进行了现场验证。
窄煤柱巷道布设在采空区侧向支承压力下,巷道开挖后底板经历了强烈的卸荷作用,卸荷作用下底板容易出现拉应力[14],弱化巷道底板稳定性。 工作面推进过程中,覆岩顶板不断发生断裂,坚硬顶板的突然断裂会对巷道围岩产生动载扰动,动载扰动下,巷道底板会伴随能量的释放与积聚从而影响底板稳定性[15]。 但目前关于窄煤柱巷道底板的卸荷特征以及动载扰动对底板稳定性影响方面的研究鲜有报道。 基于此,综合采用理论分析、数值模拟和现场实测的方法,建立窄煤柱巷道底板力学模型并分析巷道底板的卸荷及能量分布特征,以期为窄煤柱巷道底板稳定性维护带来新的思路。
1 窄煤柱巷道底板力学模型
工作面回采结束后,在采空区侧向支承压力下,实体煤内出现塑性区、弹性区及原岩应力区。 采空区形成后基本顶发生断裂,一般认为侧向支承压力峰值位于顶板断裂线下方[16]。 为了减少煤炭资源的浪费并保证回采巷道的稳定性,有时将回采巷道布设在侧向支承压力峰前塑性区内,即留设窄煤柱,如图1 所示。 对于窄煤柱巷道,尤其是深部开采,覆岩突然断裂释放大量能量,使得巷道邻空岩体发生突发式破坏,导致岩片剥落乃至岩块弹射的现象较为普遍,该种情况下可界定为巷道围岩受到了动载扰动,如图1(A、B、C 为块体)中的Fd1和Fd2,对巷帮以及底板的稳定性造成较大威胁。
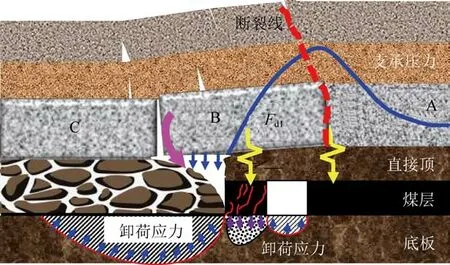
图1 窄煤柱巷道示意Fig.1 Schematic diagram of narrow coal pillar roadway
在巷道开挖前,假设侧向支承压力下的底板为弹性状态,结合图1 可得到巷道开挖前侧向支承压力作用下的底板力学模型,如图2a 所示,K1为支承压力系数,H为煤层埋深,γ为岩层平均容重。 将底板应力减去原岩应力即可得到底板应力增量,底板最大应力增量为(K1-1)γH。 窄煤柱巷道开挖相当于在侧向支承压力峰前对底板进行卸荷,因此,基于图2a 可得到窄煤柱巷道开挖后的底板力学模型,如图2b 所示。 图2 中,K1~K3为采动应力集中系数;x0为侧向支承压力峰前区长度;x1为弹性区长度;x2为原岩区长度;L为巷道宽度;x3和x4为窄煤柱的升压区和降低区长度;x5和x6为实体煤侧的升压区和降低区长度。
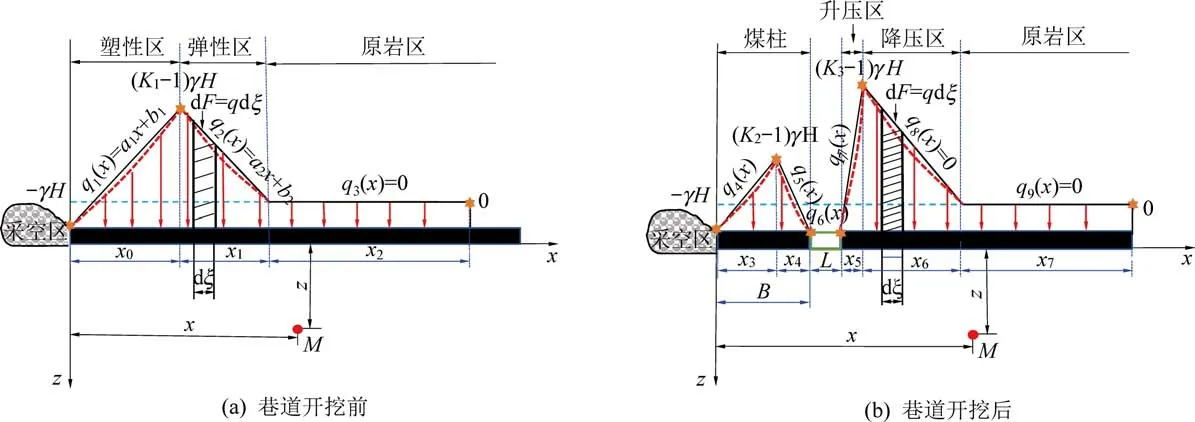
图2 巷道底板力学模型Fig.2 Mechanics model of roadway floor
为方便计算,将采动应力增量线性简化,基于弹性力学可求得底板的附加应力状态。 图2 底板力学模型中,各段线性荷载的应力增量q1(x)~q9(x)表达式为
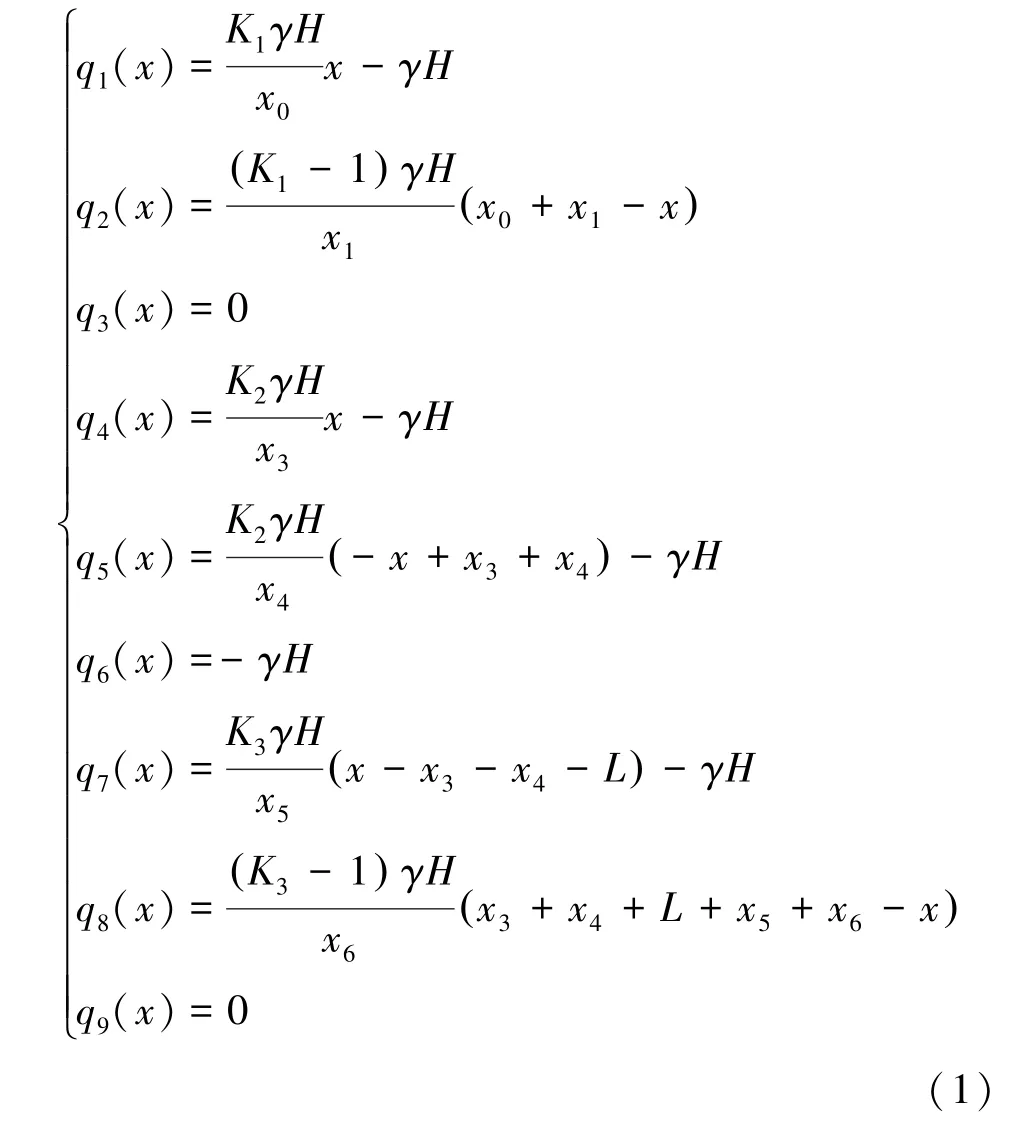
以实体煤边缘底板处为坐标原点,在侧向支承压力距原点为ξ处取微段dξ,该微段范围内的集中荷载为dF=qdξ,则各区段线性荷载作用下底板任一点M(x,z)处的附加应力(Δσx、Δσz、ΔTxz分别为水平、垂直、剪应力的附加应力)为

2 窄煤柱巷道底板应力分布特征
2.1 静载作用下底板应力分布特征
在当前开采技术条件下,窄煤柱巷道的煤柱宽度一般为5 ~8 m[17],以煤柱宽度6 m 为例进行分析。结合山西某矿地质资料数值模拟结果,选取理论模型计算参数如下:x0=4 m,x1=12 m,x2=19 m,x3=x4=x5=3 m,x6=12,x7=9,L=5 m,γ=25 kN/m3,H=550 m,k1=2.2,k2=1.5,λ=1.2。 将相关参数代入式(1)—式(3),通过Matlab 即可计算底板应力分布特征。
不考虑顶板断裂对底板产生的动载扰动,通过对图2b 力学模型进行计算得到巷道开挖后底板的主应力和剪应力分布特征,如图3 所示。 开挖后,巷道底板的应力状态呈明显的非对称分布特征,其中,实体煤底板和巷道底板的最大主应力大于煤柱底板;巷道底板的最小主应力最小,实体煤底板的最小主应力值大于煤柱底板;实体煤底板的剪应力大于巷道和窄煤柱底板,说明巷道底板靠近实体煤侧更容易发生剪切破坏。 在现场,窄煤柱巷道围岩通常发生非对称破坏,例如非对称底鼓现象,底板应力状态的非对称分布特征是其发生非对称底鼓的重要原因。

图3 巷道开挖后底板应力分布特征Fig.3 Stress distribution characteristics of floor after roadway excavation
巷道开挖相当于对侧向支承压力作用下的底板进行卸荷,卸荷导致底板沿着卸荷方向产生回弹变形,从而在底板内产生拉应力。 在岩石加载试验中,试样一般发生剪切破坏,而在岩石卸荷试验中,岩石的表面以张性裂隙为主,即岩石易发生卸荷张拉破坏,并且卸荷起点应力和卸荷量越大,岩石破坏越严重[18-20]。 因此,有必要对巷道开挖后底板的卸荷状态进行分析。 假设巷道开挖前即图2a 力学模型中底板的最大和最小主应力分别为σ′1和σ′3,巷道开挖后即图2b 力学模型中底板的最大和最小主应力分别为σ1和σ3,则开挖后底板的应力卸荷量为
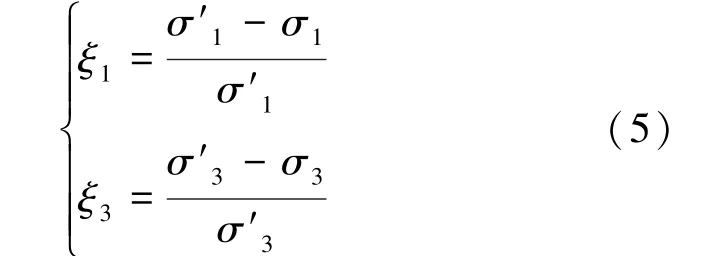
式中:ξ1为最大主应力卸荷量;ξ3为最小主应力卸荷量。
基于图2 和式(5)得到巷道开挖后底板主应力卸荷量分布情况,如图4 所示:底板最大主应力卸荷量和最小主应力卸荷量的分布规律较为一致,煤柱和巷道底板的主应力卸荷量大于0,说明煤柱和巷道底板为卸轴压和卸围压状态,其中巷道底板的主应力卸荷量最大,并且ξ3大于ξ1。 实体煤底板的主应力卸荷量小于0,为双向加载状态,并且距巷道越近加载量越高,随着底板深度增加,主应力卸荷量逐步减小,卸荷扰动烈度逐渐减弱。 开挖后,巷道底板处于一侧卸荷一侧加载的非均压状态,这对于底板的稳定性极为不利,容易导致巷道底板出现非对称破坏现象。
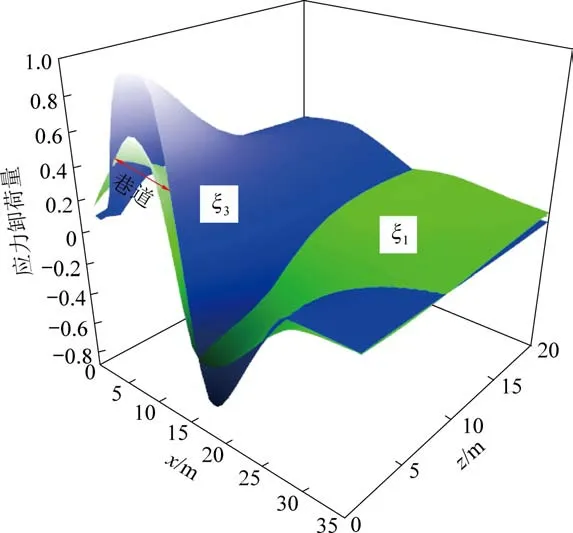
图4 底板应力卸荷量Fig.4 Stress unloading amount of floor
2.2 动载扰动对底板应力分布影响
采场大面积厚硬顶板的断裂垮落、爆破开挖以及大型设备运转等作用会对煤层及底板产生动载扰动,使得围岩的破裂更为复杂,对于深部开采,动载扰动烈度更强,对围岩稳定性的威胁更大。 针对所建立的巷道底板力学模型,假设在煤柱侧和实体煤侧底板存在2 个动载源,分别为Fd1和Fd2,如图5所示,χi为动载源Fdi所在位置。 假设井下动载为正弦波形式,波形函数为:

图5 巷道底板动载扰动力学模型Fig.5 Dynamic model of dynamic load disturbance of roadway floor

式中:Ai为震源的动载强度,MPa,i=1,2;f为频率,Hz;t为作用时间,s;T为周期,s。
动载应力波传播过程中会产生相互干涉和反射,使得传递至底板深处的应力波出现衰减,根据弹性波传播理论可知,动载源Fdi在底板任一点M所产生的动载荷增量Δσdρi为

式中:Δσdxi为第i个动载源在M点沿x方向的动载分量,MPa;Δσdzi为第i个动载源在M点沿z方向的动载分量,MPa;Δτdxzi为第i个动载源在M点的剪应力分量,MPa;αi为动载增量与竖直方向的夹角,(°)。
通过几何关系可知:

动载扰动下,底板岩体的破坏是采动静载和动载增量共同驱动下的过程,因此,结合式(3)和式(9)得到动载扰动后底板岩体的应力为:
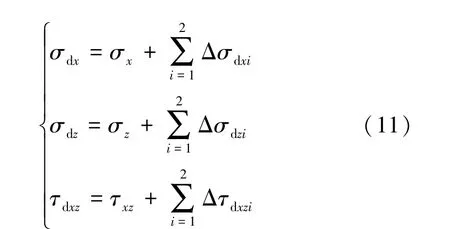
式中:σdx,σdz和τdxz分别为动静载作用下底板任一点的水平应力、垂直应力和剪应力,MPa。
由上述公式得到动载扰动下巷道底板最大和最小主应力计算公式:
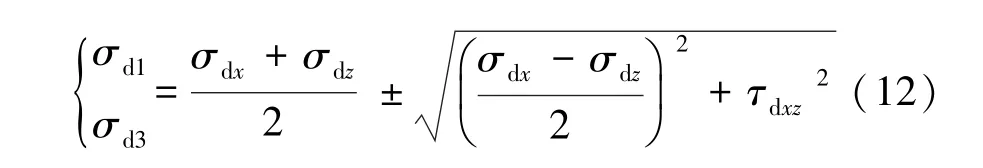
结合现场实际条件,假设两个动载源分别位于窄煤柱中心和顶板断裂线位置,即ξ1=3 m,ξ2=14 m,并令A1=3 MPa,A2=5 MPa,将相关参数代入上述公式,可得到巷道开挖后动载扰动对底板应力的影响规律,并将扰动前与扰动后底板的应力状态进行对比,如图6 所示。 动载扰动后,底板同一深度在横向上的应力分布规律变化不大,但底板各位置的应力均出现了小幅度的增加或减小现象,底板各位置的最大主应力和最小主应力均明显增加,而对于剪应力,实体煤底板靠近巷道的局部区域呈减小状态,其他区域底板的剪应力呈小幅增加状态。
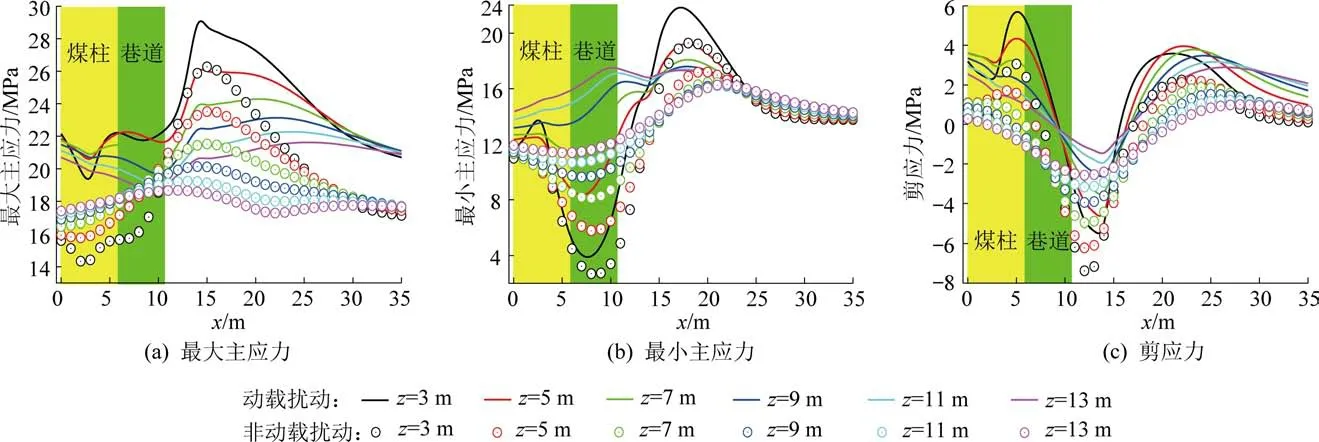
图6 动载扰动后底板应力分布特征Fig.6 Stress distribution characteristics of the bottom plate after dynamic load disturbance
3 动载扰动对底板释能状态的影响
巷道开挖后底板应力状态变化的过程中也会伴随着能量的积聚与耗散,能量的突然释放是围岩产生冲击现象的主要因素,同时大量的能量积聚现象也会对安全生产带来一定的威胁,因此,有必要分析回采后巷道围岩的能量分布特征。
在静载作用下,单位体积底板岩体可释放的弹性能U为

式中:ΔUd为底板能量增量,MJ/m3;ΔUdi为第i个动载源造成的能量增量,MJ/m3。
由图5 力学模型和式(14)可得动载扰动对底板产生的附加能量,计算结果如图7 所示。 动载扰动后,煤柱和巷道底板的能量增量大于实体煤底板,随着至煤柱水平距离的增加,底板的能量增量逐渐减小,这说明窄煤柱巷道靠近煤柱侧底板受动载扰动的影响更大。

图7 动载扰动后底板能量增量Fig.7 Energy increment of bottom plate after dynamic load disturbance
通过式(13)可计算动载扰动前底板的弹性能,设巷道开挖前底板弹性能为Uj1,巷道开挖后底板弹性能为Uj2,则巷道底板经过动载扰动后的能量释放率ξU为

当ξU>0 时,底板为释能状态;当ξU<0 时,底板为能量积聚状态。 基于式(15)得到动载扰动后底板能量释放与积聚状态,如图8 所示。 煤柱和巷道底板的能量释放率ξU大于0,为释能状态,随着底板深度增加,能量释放率逐渐减小;实体煤底板的能量释放率ξU小于0,为能量积聚状态,随着底板深度增加蓄能量逐渐接近0。 无论是能量释放还是能量积聚,均由岩体的变形导致,当岩体卸荷膨胀时会释放能量,而压缩变形时则会积聚能量。 窄煤柱巷道底板一侧为压缩蓄能状态、一侧为膨胀释能状态,这种“非均衡”状态是巷道底板失稳、非对称破坏的重要原因。 改善巷道底板两侧围岩环境的“非均衡”程度将有利于增强巷道底板的稳定性,作者认为改善巷道底板的“非均衡”程度主要有2 条思路:①增加煤柱和巷道底板的变形模量或施加补偿应力,从而减小底板的卸荷变形量和能量释放量。 ②对实体煤侧底板进行卸压,降低底板的应力集中程度和蓄能量。

图8 动载扰动后底板释能状态Fig.8 Bottom plate energy release state after dynamic load disturbance
在实际工程中,针对思路①,可对巷道底板进行注浆加固或施加预应力底板锚杆/索,注浆加固可改善巷道和煤柱底板的岩性,减少底板的膨胀变形量和能量释放量,而预应力底板锚杆/索可对底板提供补偿应力。 针对思路②,可对实体煤侧底板布设卸压钻孔或对巷道进行切顶卸压,切顶使得巷道顶板由长悬臂梁变为短悬臂梁,降低了顶板断裂线处的应力集中程度,从而减小了实体煤侧底板的应力集中程度和能量集中程度。
4 数值模拟
以山西某矿为工程背景建立数值模型,模型尺寸为255 m×220 m×145 m(长×宽×高),侧压系数取1.2。 在静载计算部分,模型四周施加水平方向约束,底部施加垂直方向约束,各岩层采用Mohr-Cou⁃lomb 本构模型。 在动载计算部分,模型顶部和底部采用静态边界,四周采用自由场边界,为减少系统自然震动,模型采用瑞利阻尼。 模型施加的动载大小和动载位置与理论计算模型一致,扰动波形为正弦波,频率为20 Hz,作用时间为0.05 s 即1 个动载周期,底板力学参数见表1。
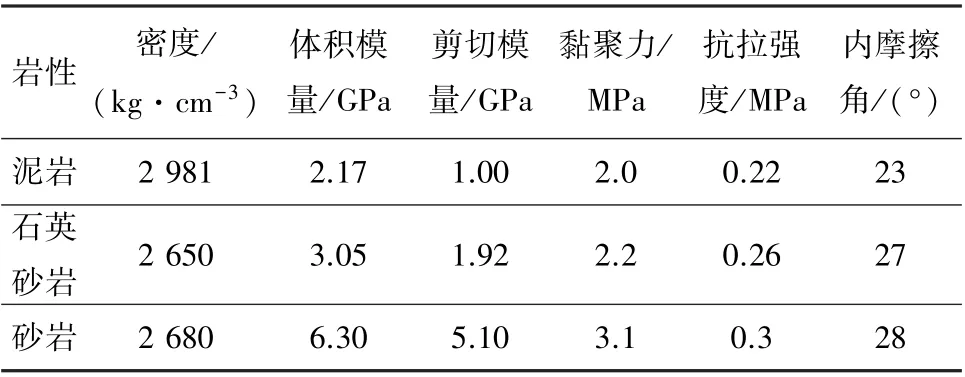
表1 岩层物理力学参数Table 1 Rock physical and mechanical parameters table
动载扰动前后底板的垂直位移如图9 所示,在静载作用下,巷道两侧底板的垂直位移呈明显的非对称状态,实体煤底板垂直位移向下而煤柱和巷道底板垂直位移向上。 这主要因为实体煤底板应力高于煤柱和巷道底板,同时,巷道开挖后,巷道和煤柱底板为卸荷状态,而实体煤底板为压缩状态,根据滑移线理论,在实体煤侧高应力挤压作用下,底板岩体将向应力较小的巷道和煤柱底板方向移动,从而导致巷道和煤柱底板的垂直位移更大。 在动载扰动作用下,实体煤和煤柱底板的垂直位移变化不大,而巷道的底鼓量明显增加,底鼓量增加幅度主要体现在靠近煤柱一侧,导致巷道的非对称底鼓程度进一步增加,由此可见,动载扰动对窄煤柱巷道底板变形量影响较大,工程中应给予重视。
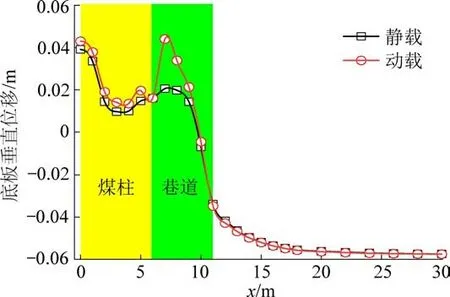
图9 动载扰动前后底板位移Fig.9 Base plate displacement before and after dynamic load disturbance
动载扰动前后底板破坏特征如图10 所示,在静载作用下,由于巷道开挖的卸荷作用,巷道浅部底板为张拉破坏,深处为剪切破坏,并且巷道底板呈非对称破坏特征,其中靠近实体煤侧的破坏深度大于煤柱侧。 在动载作用下,巷道底板的破坏范围有所增加,但巷道底板的非对称破坏特征未发生改变。
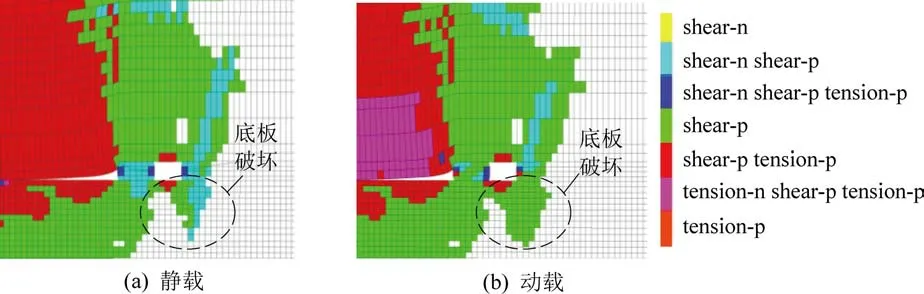
图10 动载扰动前后底板破坏特征Fig.10 Failure characteristics of bottom plate before and after dynamic load disturbance
5 工程验证
山西某煤矿4 煤层平均埋深183 m,平均煤厚9 m,采用综采放顶煤回采工艺。 以往工作面回采巷道采用宽煤柱护巷,煤柱宽度为30 m,为提高煤炭采出率,4209 工作面采用窄煤柱护巷技术,煤柱宽度为5 m,回采巷道为矩形断面,尺寸为5 m×3.6 m(宽×高)。 巷道采用锚索网联合支护,顶板采用ø18 mm×2 200 mm 的螺纹钢锚杆,间排距为900 mm×1 000 mm,此外,顶板每排布置2 根ø17.8 mm×5 700 mm锚索,间距为2 m;巷道两帮均采用ø18 mm×2 200 mm 的螺纹钢锚杆,间排距为900 mm×1 000 mm;巷道底板无支护。
回采期间,工作面前方底板发生严重底鼓变形,平均底鼓量650 mm,巷道最大底鼓量达850 mm。由前文知,巷道底板两侧的“非均衡”应力环境是窄煤柱巷道底板破坏、大变形的主要原因。 为了改善巷道底板两侧围岩环境的“非均衡”程度,结合锚杆索力学性质、巷道围岩物理力学性质和以往的支护案例,确定了针对该条巷道的非对称支护方案:顶板采用ø22 mm×3 100 mm 的螺纹钢锚杆,间排距为800 mm×900 mm,顶板锚索非对称布置,煤柱侧间距1 400 mm,实体煤侧间距1 800 mm,锚索采用ø17.8 mm×8 300 mm 的钢绞线;两帮锚杆采用非对称支护,间排距为700 mm×800 mm,窄煤柱帮采用ø22 mm×3 100 mm 的螺纹钢锚杆,实体煤帮采用ø22 mm×2 400 mm 的螺纹钢锚杆,支护方案如图11所示。
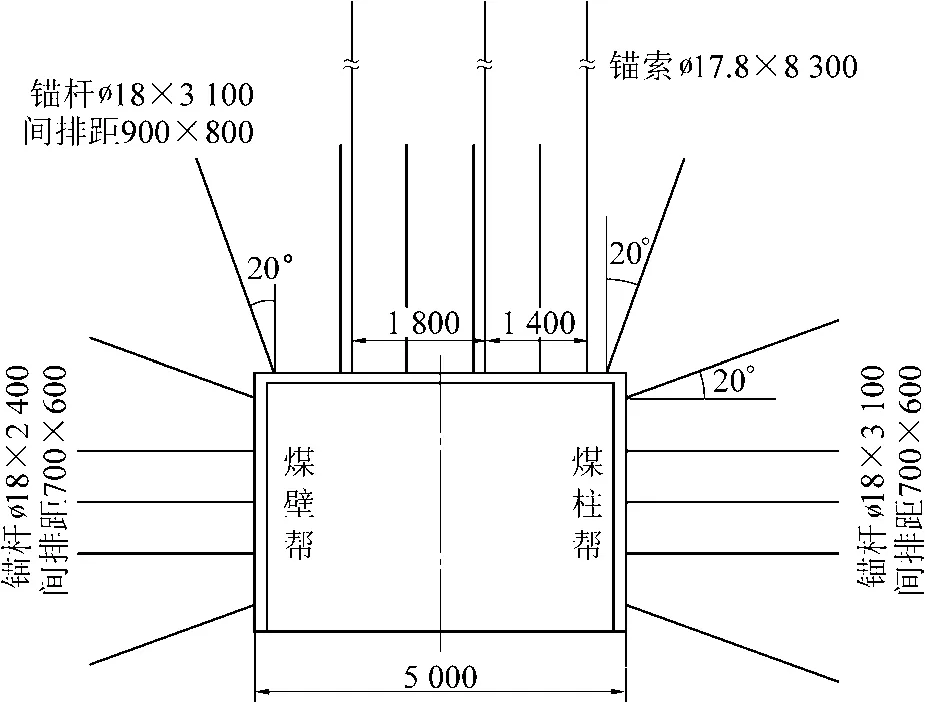
图11 非对称支护方案Fig.11 Asymmetric support scheme
为减小巷道煤柱侧底板的膨胀变形量,在煤柱侧底板变形严重区域进行注浆加固,增加底板岩体的变形模量,浆体凝固后可为底板提供“支护抗力”,减小底板的卸荷变形量和能量释放量。 同时,在底板变形严重区域增挖了卸压槽,卸压槽一方面可以为底板提供变形空间,另一方面,当巷道受到动载扰动时,卸压槽可以释放动载扰动能量,防止巷道发生冲击破坏。
4209 工作面推进长度为2 685 m,工作面推进至1 350 m 时,矿方采用了上述支护方案对回采巷道进行了补强支护并进行注浆加固等措施,加固前与加固后底板变形量的对比情况如图12 所示。 相比加固前,巷道底鼓量得到了有效控制,满足了工作面生产需求。
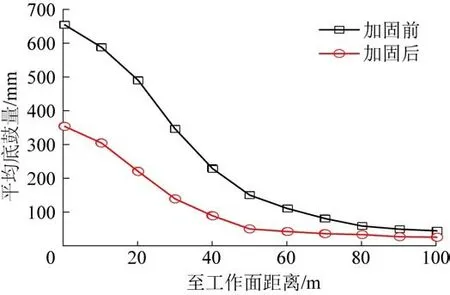
图12 非对称支护方案Fig.12 Asymmetric support scheme
6 结 论
1)开挖后,窄煤柱巷道底板应力呈非对称分布特征,实体煤底板和巷道底板的主应力和剪应力大于煤柱底板,巷道底板靠近实体煤侧更容易发生剪切破坏。 巷道开挖后,煤柱和巷道底板处于卸轴压和卸围压状态,实体煤底板为双向加载状态。
2)动载扰动后,煤柱和巷道底板的能量增量大于实体煤底板,靠近煤柱侧底板受动载扰动的影响更大。
3)在动载扰动条件下,煤柱和巷道底板的能量释放率ξU大于0,为释能状态,实体煤底板能量释放率ξU小于0,为能量积聚状态。 窄煤柱巷道底板一侧为压缩蓄能状态、一侧为膨胀释能状态,这种“非均衡”状态是巷道底板失稳、非对称破坏的重要原因。
4)实践表明,通过非对称支护技术,并对煤柱侧底板进行注浆加固,减小底板的卸荷变形量和能量释放量即改善底板“非均衡”状态可有效控制底鼓量。
