具有速度调节机制的船舶事件触发编队控制

张国庆 刘上 郎雷 张卫东

(1.大连海事大学航海学院,辽宁大连 116026;2.沈阳新松机器人自动化股份有限公司,辽宁沈阳 110169;3.上海交通大学自动化系,上海 200240)

1 引言

近年来,随着智能控制理论在船舶上的广泛应用,欠驱动船舶编队控制逐渐成为控制领域的热点问题之一,并且受到了众多学者的关注[1–2].与传统的单艘船舶路径跟踪控制相比,多艘船舶的编队控制具有更广泛的应用背景和潜在优势,如军舰协同作战、领海巡逻、海事搜救作业和海洋资源勘探等.目前,领导–跟随法因具有简单灵活、可伸缩、易于工程应用的特点从而被广泛研究.但是,在海洋实践中,受限的通信带宽和船舶编队间速度协调困难可能会造成控制系统稳定性降低甚至导致整个编队失效[3].因此,为了提高船舶编队在自主航行任务中的安全性,本文旨在研究一种具有速度调节机制的事件触发编队控制算法,对其在海洋工程领域中的应用具有实际意义.

为了实现海洋环境下多艘欠驱动船舶的编队控制,国内外许多学者开展了相关研究并取得了丰硕的成果[4–6].Shojaei[7]基于李雅普诺夫直接法提出了一种神经网络编队控制算法,通过构造辅助函数有效地防止了跟踪误差的增长并通过重建运动学和动力学回路消除相关的饱和影响.针对(line-of-sight,LOS)视角和视距约束问题,Jin[8]提出了一种容错有限时间控制器,能使船舶编队在有限时间内稳定至计划航线上.为了进一步估计船舶的未知状态,Fu等[9]提出了一种基于有限时间扩展状态观测器的分布式船舶编队控制算法,并且根据所测状态引导船舶编队跟踪时变虚拟领导船.

在上述文献中[4–9],主要存在两类问题亟待解决.第1类问题是控制输入频繁抖振问题.在海洋环境下,欠驱动船舶会因实时镇定海洋环境扰动造成控制输入抖振现象,这样不仅增加了执行装置的磨损程度还会产生不必要的信道占用.文献[10]提出了一种同时考虑输入饱和和驱动器故障的船舶事件触发路径跟踪控制算法,从而使控制器能够根据预先设定的触发条件更新.在文献[11]中,张国庆等为解决船舶动力定位控制问题设计了一种考虑事件触发输入的控制器,并且通过引入鲁棒神经阻尼技术对模型不确定项进行学习训练,从而避免了对大量神经网络权重的在线更新;第2类问题是领导船速度信息不可知、跟随船速度不可控的问题.在实际航行中,船舶编队可能在某些特殊的情况下需要领导船采取加速或者减速措施,从而使跟随船不能合适地调整航速跟踪领导船.此外,领导船的位置信息和方位信息通常可以由GPS和电罗经测得,但是领导船的速度信息是不可测的.因此,如何在不需要领导船速度信息的约束下执行编队任务对欠驱动船舶编队控制系统来说是十分有必要的.

基于以上分析,本文提出了一种具有速度调节机制的欠驱动船舶事件触发编队控制算法.在控制器设计中,采用径向基神经网络(radial basis function neural networks,RBF–NNs)对系统模型不确定部分进行逼近,并设计了一种满足控制器与神经网络权重估计器同步触发的事件触发机制,减少了通信频道的占用次数和控制输入频繁抖振频次.同时,针对现有领导–跟随方法中存在的领导船速度信息不可知、跟随船速度不可控的问题,设计了一种自适应速度调节器.这能够提高在实际海洋工程中的应用性.最后通过李雅普诺夫理论分析和仿真对比实验验证了闭环控制系统的有效性和鲁棒性.

2 基础知识

在本文中,|·|表示绝对值,∥·∥表示Euclidean范数,表示(·)的估计值,并且

2.1 欠驱动船舶的非线性数学模型

对于欠驱动水面船舶,其数学模型通常需要考虑船舶前进、横漂和艏摇3个自由度的平面运动[12].由于欠驱动船舶仅配备螺旋桨和舵两个驱动装置,故船舶模型具有欠驱动特性.根据牛顿力学和拉格朗日力学,欠驱动船舶的非线性数学模型表达式可以描述为式(1)–(2).

式中:η=[x y ψ]T表示惯性坐标系下船舶的位置和艏摇角;v=[u v r]T表示在附体坐标系下船舶的前进速度、横漂速度和艏摇速度;n,δ为船舶控制系统的实际可控输入,即主机转速和舵角;dwu,dwv,dwr为海洋环境扰动;mu,mv,mr,du1,dv1,dr1,du2,dv2,dr2,du3,dv3,dr3为未知模型参数,用来描述船舶固有质量、附加质量和水动力阻尼;fu(v),fv(v),fr(v)为非线性函数,用来描述模型中的任意不确定性;Tu(·),Fr(·)为船舶系统未知增益.

考虑到实际海洋工程需求,本文作如下假设:

假设1[2]假设欠驱动船舶横漂运动自动满足一致耗散有界特性.

2.2 RBF神经网络

在控制工程中,径向基神经网络是一种典型的未知函数逼近器[13],能有效重构任意非线性函数.因此,本文引入RBF神经网络逼近系统模型不确定项并且引入以下引理.

引理1[14]对于在紧集Ωx中任意给定的连续光滑函数f(x)(f(0)=0),利用RBF神经网络和连续函数分离技术可以将f(x)以任意精度逼近为

式中:W=[w1w2··· wl]T为理想参数权重;S(x)=[s1(x)s2(x)··· sl(x)]T表示高斯函数,具体表达形式如式(4)所示;ε(x)表示未知逼近误差,且有逼近误差上界;l>1为神经网络节点数量;µ和ξ分别表示高斯函数的中心和宽度值

3 自适应事件触发控制器设计

3.1 自适应速度调节器

在领导–跟随框架中,针对领导船速度信息不可知、跟随船速度不可控的问题,设计了一种自适应速度调节器,通过对船舶的期望速度上界自适应补偿,能够确保跟随船仅需要领导船位置和艏向信息的情况下,以较高精度跟踪上领导船.所设计的领导–跟随框架如图1所示.

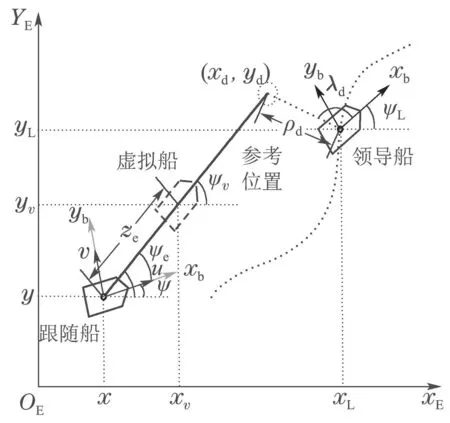
图1 领导–跟随框架原理图Fig.1 Schematic diagram of the leader-following framework

在惯性坐标系下,跟随船的参考位置ηd可以根据领导船位置ηL和期望视距ρd、期望视角λd获得.其具体表达式如式(5)所示.

其中:领导船位置向量ηL=[xLyLψL]T;跟随船参考位置向量ηd=[xdydψd]T;位置配备向量ℓ=[ρdcosλdρdsinλd0]T.R(ψL)为领导船的旋转矩阵.根据式(5),参考位置向量的运动学模型如式(6)所示.

式中:跟随船的速度向量为vd=[uL−rLρdsinλdvL+rLρdcosλdrL]T.uL,vL和rL分别表示领导船的前进速度、横漂速度、转艏角速度.值得注意的是,vd中包含了领导船的速度信息,因此,在跟随船和参考位置之间设计一个虚拟船ηv,通过设计自适应速度调节器实时调节跟随船航速,能够为跟随船提供合理的位置信号和方位信号.虚拟船的运动学模型可以描述为式(7).

式中:ηv=[xv yv ψv]T.定义虚拟船跟踪参考信号的误差为ηe=ηd−ηv.ϑv为速度调节器,其具体表达式如式(8)所示.

式中:Kv∈R3×3为人为设定的控制参数矩阵;ζv为参考速度vd的上界,即∥vd∥≤ζv;ϵv为一个正常数.速度调节器可以由自适应律(9)在线补偿

为了稳定跟踪误差ηe,引入李雅普诺夫函数如式(10)所示.

利用式(6)–(7)对V0求导,可以得到式(11).

根据∥R(ψ)∥=1,式(8)–(9)和不等式∥vd∥≤ζv可以得到式(12).

从式(12)容易看出,通过合适地调整控制参数Ke和σv,可保证ηe和满足半全局一致最终有界收敛.

3.2 控制器设计

欠驱动船舶编队控制器设计过程分为两步:1)采用李雅普诺夫直接法设计运动学回路的虚拟控制律;2)基于RBF神经网络和事件触发机制构造动力学回路的控制器,最终设计出符合海洋工程实践的控制器和自适应学习参数.

步骤1定义船舶编队的跟踪误差为式(13).{

式中:(xv,yv)为虚拟船的位置坐标;ψr为实际船舶相对于虚拟船的方位角,ψr∈(−π,π].

根据实际船舶与虚拟船的位置关系,可以进一步得到式(14).

根据式(14),分别设计u,v方向上的虚拟控制律αu,αr如式(15)所示.

式中:kze>0,kψe>0为设计参数.δxy >0的引入使实际船舶跟踪虚拟船但不超越虚拟船.值得注意的是,虚拟控制律αu和αr的微分表达式是难以获取的,因此将虚拟控制律分别通过时间常量为Tu,Tr的一阶低通滤波器βu,βr,如式(16)所示.

定义动态面误差为qi=αi −βi,i=u,r.动态面误差的导数可以表示为

Ei(·),i=u,r为连续函数.由于船舶编队在海上航行时会受到水动力阻尼的作用,且u,v,r为有界变量.因此,Ei(·)存在未知上界Mi,即Ei(·)≤Mi,i=u,r.

步骤2定义动力学误差变量ue=βu −u,re=βr −r.根据式(2)–(3),动力学误差的时间导数可以表示为式(17).

由于海洋环境的扰动和连续时间系统实时镇定的特性,会增加通信信道的占用频次和控制输入的频繁抖振,甚至导致执行装置的严重磨损.因此,受文献[15]中思想的启发,本文设计了一种满足控制器与神经网络估计器同步触发的事件触发机制,如式(18)–(19)所示,能够进一步缓和通信频道的占用情况

因此,针对主机转速n和舵角δ,设计实际控制输入式(22),虚拟控制律(23)和自适应学习参数(24).

4 稳定性分析

定理1针对欠驱动船舶运动数学模型(1)–(2),假设1–2成立,利用事件触发规则(18)–(19),实际控制输入(22),虚拟控制律(15)(23),自适应学习参数(24)和神经网络权重估计器(25)构建闭环控制系统,可以保证闭环控制系统中所有的变量能够满足半全局一致最终有界(semi-global uniform ultimate bounded,SGUUB).

证为了分析闭环控制系统的稳定性,构造误差变量的李亚普诺夫函数如式(26)所示.

利用式(14)–(15)(17)(23)(25)对式(26)求导,可以得出式(27).

为了进行下一步的放缩设计,利用杨氏不等式引入式(28)–(30).

根据事件触发测量误差(21),则不等式(31)成立.

根据利普希茨条件和式(18),以下不等式成立:

根据式(32)–(34),以下不等式成立:

因此,结合式(18)(31)(35),最终可以得出式(36).

式中:

进一步可以将式(41)改写为式(42).

式中

通过对式(42)进行积分,可以得到

因此,闭环控制系统的所有误差能够保证通过合理的调节控制参数最终实现SGUUB收敛. 证毕.

为了证明所提算法能够避免Zeno现象需要证明触发时间间隔{tj+1−tj},∀j∈Z+,小于某一正常数.根据事件触发条件(18),可以得到式(43).

因此,本文提出的控制算法避免了Zeno现象.

5 仿真实验

为了验证本文提出的事件触发编队控制策略的有效性和优越性,本节通过MATLAB仿真平台,在基于机理模型的海洋环境下与文献[16]中的控制算法进行对比实验.仿真对象为一艘欠驱动水面船,船长38 m,质量118×103kg,其他参数详见文献[17].

在仿真实验中,为了构造更加符合实际的海洋环境,本文采用了文献[12]中的方法,即挪威石油工业组织规范构建风干扰模型和联合北海波浪计划构建风生浪干扰模型.模拟海浪的JONSWAP(joint north sea wave project)波谱如图2(a)所示,其中主风向为45◦,主风速为9.8 m/s,3D海面波浪如图2(b)所示.

图2 海洋环境干扰Fig.2 Marine environment disturbance

仿真结果如图3–7所示.图3给出了船舶编队轨迹的二维平面图,为了证明本文算法的优越性,将领导船与文献[16]中的控制算法进行对比,从局部放大图中可以看出,本文控制算法具有更好的跟踪性能;图4为控制输入n和δ的对比曲线,与文献[16]中的控制效果相比,本文所提算法操纵执行器设备的频次较少;图5描述了本文所提算法中神经网络权重估计器的欧几里德范数曲线,可以看出本文设计的事件触发机制不仅能使控制器触发采样还能够使神经网络权重事件触发,这能够进一步减少信道占用次数;图6为事件触发采样间隔记录对比图,与文献[16]中的触发效果相比,本文所提出的事件触发机制触发频次少、采样间隔长;为了体现当领导船改变速度时跟随船的速度响应性能,图7给出了仿真时刻为20 s时,领导船的期望前进速度由5 m/s增加至10 m/s跟随船的速度响应性能曲线.显然,在自适应速度调节器(8)的作用下,尽管20 s 时刻领导船期望速度发生突增,但是跟随船仍能以合理的速度跟随领导船.

图3 船舶编队轨迹对比曲线Fig.3 Comparison of the ship formation trajectories

图4 控制命令对比效果Fig.4 Comparison of control order efforts

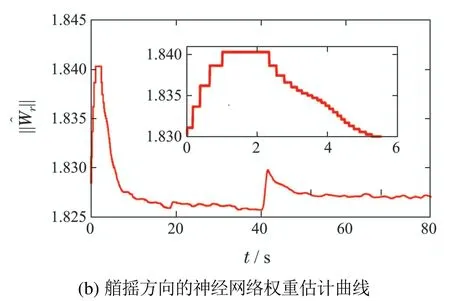
图5 神经网络权重估计曲线Fig.5 NN weight estimator curve

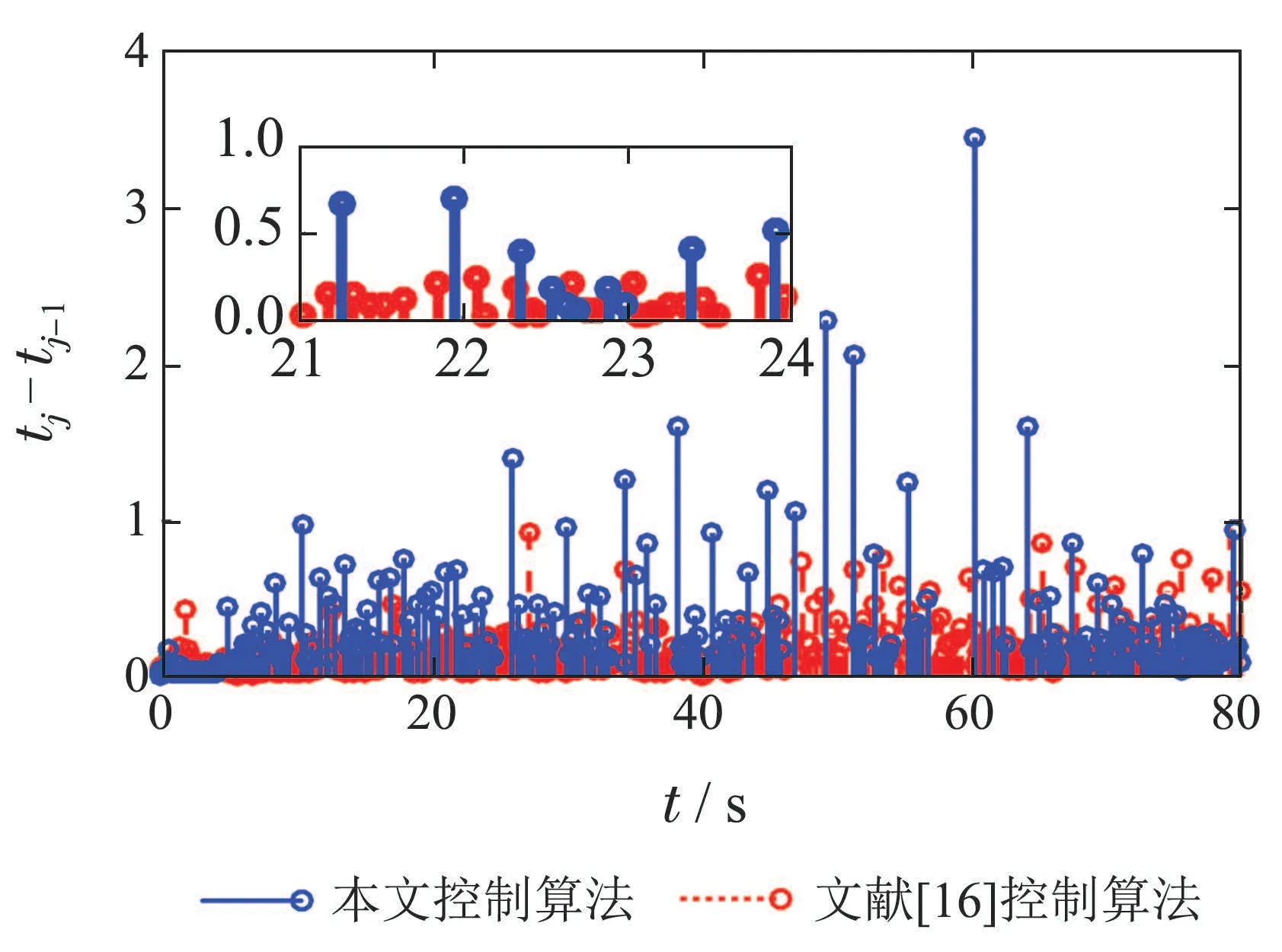
图6 事件触发采样间隔对比效果Fig.6 Comparison of time interval between the two adjacent event-triggered sampling points

图7 跟随船速度响应性能曲线Fig.7 Response curve of the follower’s velocity performance

6 结论

本文针对欠驱动船舶编队控制问题,设计了一种具有速度调节机制的事件触发编队控制算法.该算法中,一种速度调节器被用来解决领导船速度信息不可知、跟随船速度不可控的问题.利用RBF神经网络和事件触发机制处理模型不确定和通信资源受限问题,并且能够保证控制器和神经网络权重估计参数同步触发.所提出的事件触发控制算法在保证系统鲁棒性的同时减少了通信信道的占用次数,能够缓和执行器磨损严重的问题.最后,通过仿真实验验证了所设计控制算法的合理性.