深度确定性策略梯度与模糊PID的协同温度控制

吴敏 ,王晓璐 ,姜玉东 ,钟磊 ,莫飞扬

(1.金陵科技学院机电工程学院,江苏南京 211169;2.江苏时代新能源科技有限公司,江苏溧阳 213300;3.澄瑞电力科技(上海)有限公司,江苏南京 211100)

1 引言

随着科学技术的发展,温度控制被广泛应用于各技术领域,实施集中供暖、合理利用资源、提高能源利用效率是加快城市现代化的有效措施和重要途径.集中供热已成为中国北方冬季供暖的主要形式,并得到越来越广泛的应用.该供暖是使用热网连接大量热用户,通过均匀热源提供必要热量,是一个大滞后、时变、非线性的复杂系统,需要寻求更加先进有效的控制方法.文献[1–2]将模糊控制与经典PID调节器相结合,具有模糊控制的灵活性和适应性,提高了系统的控制精度,但模糊PID在控制大滞后系统时,控制器不能立刻对产生的干扰起到抑制作用,且无法保证大滞后系统的稳定性.针对大滞后系统的控制,文献[3]提出了一种模糊Smith预温度控制系统,通过估计器来补偿模型延迟,然而Smith预估器的建立需要准确建立系统模型,否则会降低控制系统的稳定性.文献[4]采用自整定模糊PID算法和闭环负反馈结构,被控系统可获得良好的动态性能.针对温度控制方法的研究,受到国内外的广泛关注[5–11],但温控系统由于系统输入信号突变、系统电路工作中存在电磁干扰、温度采集端的误差和输入电源电压的波动等因素导致温度控制系统中存在剧烈频繁的干扰以及大滞后时,很难对温度系统进行精确控制.针对此问题,本文提出深度确定性策略梯度与模糊PID的协同温度控制,对模糊PID控制系统引入了基于深度确定性策略梯度(deep deterministic policy gradient,DDPG)的辅助控制器,利用DDPG算法进行在线权值学习能力,对系统执行器进行辅助控制,实现自动补偿温控系统的不确定性和干扰,通过主辅双控制器的联动控制,实现控制系统的快速响应、减少误差和超调量.

2 温度控制系统控制策略

2.1 温度控制系统实验模型

恒温控制监控系统的数学模型可准确反映其温度的实际特性,可为恒温温度控制系统的设计和参数整定提供理论依据,恒温控制系统为单输入、单输出的系统,该系统具有纯滞后环节和自平衡,其数学模型可使用一阶系统加纯滞后环节来描述,传递函数为

式中:K表示静态增益,T表示时间常数,τ表示纯滞后时间.在稳定状态下,控制对象输入与输出呈线性关系,当控制对象的自平衡能力越大时,静态增益K就会越小,反之亦然.当系统具有一个阶跃输入量时,输出量从一个稳定状态到达另一个稳定状态的时间是时间常数T,它表示被控对象所具有的惯性特征,T值越大,系统变化所需的时间越长,反之亦然.如果输入量产生变化后,输出量跟随发生变化所需的时间就是滞后时间τ,它表示输出响应落后激励输入的时间,滞后时间τ主要是由于热量传递和输送不能马上完成而导致.

温度控制闭环反馈控制系统模型如图1所示,由推导可知系统的输出为

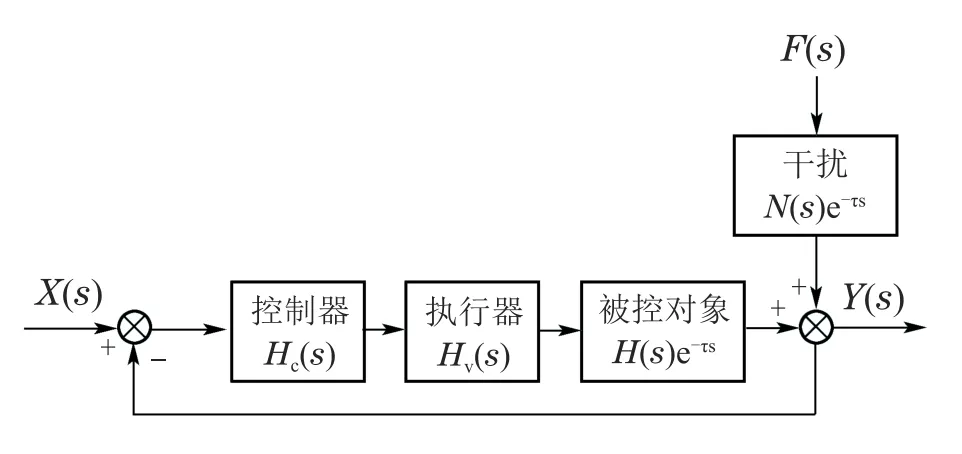
图1 闭环控制系统模型Fig.1 Closed-loop control system model

由式(2)可知,系统中存在的干扰量F(s)会令被控量Y(s)产生偏差,同时由于系统滞后项e−τs的存在,控制器不能立刻对干扰量进行控制,从而极大的影响了系统的控制精度和稳定性.

图1中:Hc(s)表示控制器传递函数,Hv(s)表示执行器传递函数,H(s)表示被控对象的传递函数,e−τs表示控制对象系统延迟,F(s)表示系统噪声的传递函数,X(s)表示系统期望输入,N(s)表示系统噪声,Y(s)表示系统输出.系统中干扰F(s)的存在,导致系统输出Y(s)与实际产生较大误差,此外,系统的调节也存在着滞后性,为控制系统的精度与稳定性带来极大挑战.

2.2 系统控制策略原理

PID控制算法有着简单、稳定、控制效果好的优点,被广泛应用于工业控制中.然而传统PID控制算法缺乏在线学习的能力,控制器不能对设置过的PID参数进行更改,对于不确定环境的系统控制无法获得最优性能.为了在不确定环境中获得最佳控制效果,本文采用主控制器加辅助控制器的控制结构,将模糊PID作为主控制器,DDPG算法作为辅助控制,控制结构如图2所示.

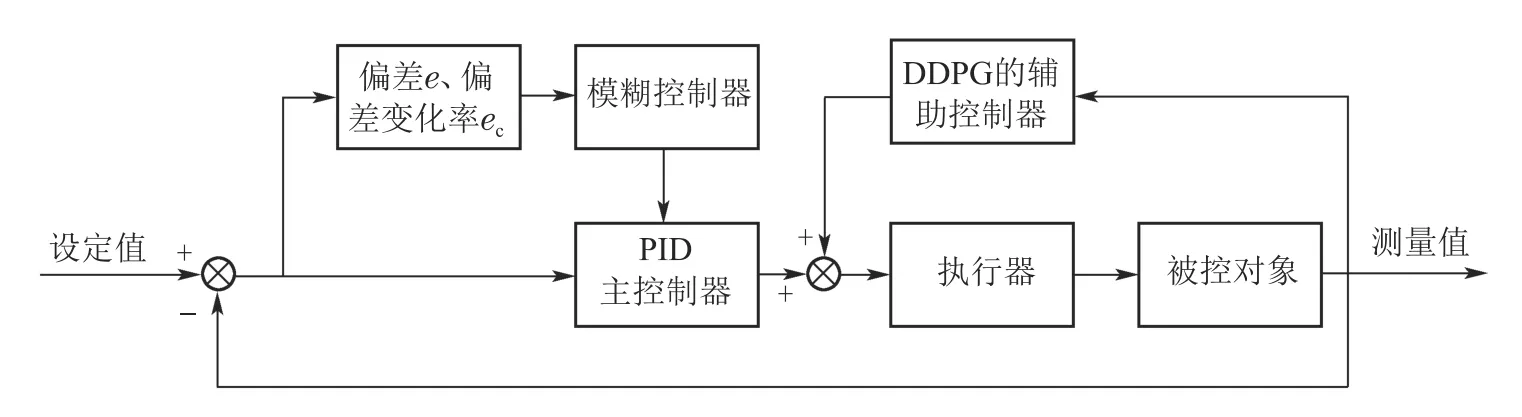
图2 基于DDPG与模糊PID的控制结构Fig.2 Control structure based on DDPG and fuzzy PID

首先,当给被控对象施加阶跃信号时,PID主控制器和DDPG辅助控制器会同时输出执行器的控制量;然后,当被控对象反馈产生较大变化时,PID主控制器的微分控制会抑制主控制器的输出;接着,DDPG辅助控制器会根据执行动作后的温度值和奖励值为被控对象快速找到一个大约的控制量;最后,当被控对象接近设定值且反馈变换较平缓时,主控制器和辅助控制器再根据偏差的大小对系统进行微调,使得被控对象达到所需的设定值.

3 模糊PID主控制器设计

3.1 模糊控制器

模糊自适应PID控制是将模糊自适应控制理论与PID控制理论相结合应用于温度控制系统[12–14],首先制定模糊规则,然后以偏差信号和偏差信号变化率作为输入进行模糊推理,在此基础上输出对PID控制有调节作用的修正因子,从而实现对PID控制器的自适应调整[15–16],充分发挥两种控制策略各自的优势,提高温度控制系统的性能.温度控制系统将温度设定值与温度回采值分别设置为二维输入(系统温度给定值与测量反馈值的偏差e(t)、偏差信号变化率ec(t))和三维输出(比例系数kp、积分系数ki、微分系数kd),系统通过监测e(t)和ec(t)的值而对模糊PID控制器的参数进行实时修改,进而优化其控制性能.

模糊自适应PID算法的核心是模糊控制器的设计,要在系统运行过程中找出模糊控制器的输出参数kp,ki,kd与偏差信号e(t)及偏差信号变化率之间的模糊关系,模糊控制主要包括3个部分:模糊化、模糊推理和清晰化处理,主要有5个变量:偏差信号e(t)、偏差信号变化率ec(t),kp,ki和kd,其中e(t)和ec(t)作为模糊控制器的输入,kp,ki,kd作为模糊控制器的输出并作为PID控制的修正因子.

针对温度控制系统,偏差信号e(t)通过传感器回采当前温度值与目标设定值的运算得到,再把偏差信号e(t)与偏差信号变化率ec(t)进行模糊化,得到相对应的模糊量,然后按照模糊规则经过推理得出模糊控制量,最终为了对被控对象进行精确的控制而进行清晰化处理得到kp,ki和kd.

3.2 PID参数整定

模糊PID隶属函数的幅宽影响系统的控制性能,当隶属函数的斜率较大时,系统的输出较为剧烈、灵敏度高,当斜率较小时,系统稳定性强,需要依据操作者的经验和实际系统来确定隶属函数具体的幅宽.

为提高温度系统的控制精度,本文采用遗传算法对模糊PID的隶属函数和模糊规则进行优化.遗传算法是一种基于自然选择原理和遗传机制的迭代式自适应最优求解算法,可提高温度系统的控制性能[17–19],基于遗传算法的PID参数整定步骤如下所示:

(1)模糊域编码

温度偏差e(t)的实际范围可能到达−100∼100◦C,因此,其论域定为[−100,100],由于温度变化缓慢,温度偏差变化率的基本论域大致为[−2,2],经参数整定分析输出量kp,ki,kd实际论域设为[−1,1],[−0.02,0.02],[−0.3,0.3];输入、输出的模糊论域均设为[−6,−5,−4,−3,−2,−1,0,1,2,3,4,5,6].系统设定为负大NB、负中NM、负NS、零ZO、正小PS、正中PM、正大PB的7个语言变量值,并用0,1,2,3,4,5,6进行编码表示.

(2)初始种群选取

依据设定值对初始种群参数范围进行设置,将初始种群最优解参数范围设为[0,6],并在设定范围内随机生成规模为100的初始种群.

(3)适应度函数选取

适应度函数通过对个体特征的判断从而判断个体的适应度,通过个体的适应度作为评价PID参数的好坏标准,本文将系统的动态偏差、超调量和调整时间性能指标作为目标函数,从而将基于适应度函数描述为

式中:e(t)是系统偏差,u(t)是控制器输出,tu是系统响应时间,ω1,ω2,ω3为加权常数.

(4)选择遗传算子

本文通过轮盘赌选择法来确定从父代群体遗传到下一代群体.轮盘赌选择法是利用整体种群中个体适应度值与整体适应度值的比例,来确定被选择的概率,公式如下:

其中:Pi是个体i被遗传选择的概率,fj是所有个体叠加的整体适应度值,fi是个体i的适应度值.

(5)交叉和变异操作

遗传算法通过交叉操作将两个互相配对的个体按照某种方式相互交换部分基因,本文将交叉概率设为0.86,采用两点交叉算法,从而形成两个新的个体.同时为提高局部搜索能力,将变异概率设为0.04,采用变异运算改变个体某些基因值来产生新的个体.

4 DDPG辅助控制设计

4.1 DDPG算法

为了使系统实现快速响应、减少误差、减小超调量,本文采用DDPG算法的辅助控制.DDPG算法是一种深度强化学习算法,分别建立策略网络和价值网络,通过策略网络来生成执行器的行为策略,价值网络来评判动作好坏,从而指导系统执行器的动作[20–22],DDPG算法结构框图如图3所示.

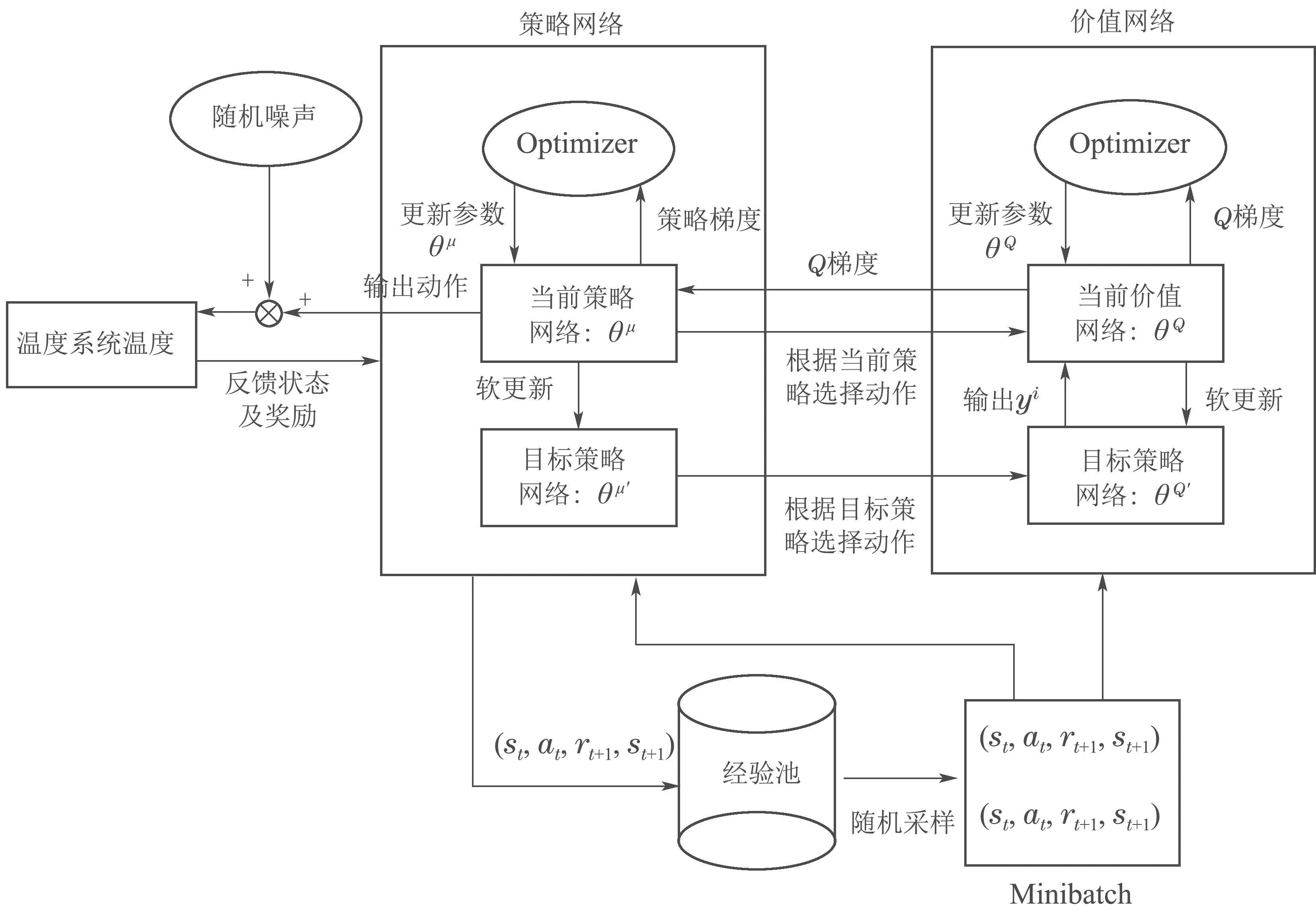
图3 DDPG算法结构框图Fig.3 Block diagram of DDPG algorithm structure

策略网络将输出值拷贝给价值网络,价值网络目标是选出最佳的动作值,价值网络以损失函数最小化为目标来更新网络参数

式中:J(θQ)为价值网络损失函数,yi为价值网络计算的目标动作价值,n为采样数量,ωk为样本权重,Q(st,at/θQ)为样本在状态st时采取的动作at,rt+1为t+1时刻的奖励,γ为折扣因子.

策略网络和价值网络中分别都包含了一个现实网络和一个目标网络,在训练完一个批次的数据后,DDPG算法通过SGA/SGD算法来更新现实网络参数,再实现目标网络的参数更新.

4.2 DDPG辅助控制器

DDPG算法通过温度控制系统获得样本数据(st,at,rt+1,st+1),其中:st是在t时刻温度控制系统的温度值,at是系统在st状态下所执行的动作,rt+1是系统在状态st下执行动作at的奖励值,st+1是温度控制系统在执行动作at后的系统温度值.将样本数据放入经验池中,再随机从经验池中采样最小批量数据进行学习、更新,最后DDPG辅助控制器的执行动作如下式:

式中:Nt是随机噪声,函数µ(st|θµ)为最优行为策略,θµ代表策略网络参数.DDPG辅助控制器主要用于补偿温度控制系统的温度跟踪误差,改善模糊PID主控制器的控制性能,DDPG网络的参数如表1所示.

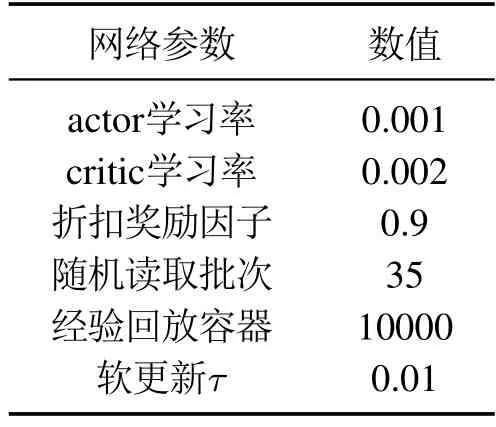
表1 DDPG辅助控制器的参数置Table 1 Parameter setting of DDPG auxiliary controller

其中,学习率越大,网络误差对参数的影响越大,容易发散网络,因此选取0.001作为actor网络的学习率,选取0.002作为critic网络的学习率;过大的折扣奖励因子可以对温度预测越敏感,但太大的折扣因子会影响网络的预测精度,折扣奖励因子选为0.9;经验回放容器是记忆回放缓存中存放的最大容量,若超过10000,程序会自动删除旧的记忆来维持容量稳定.

5 仿真结果

基于上述理论,本文将遗传算法的迭代次数设为100次,经过100次的迭代计算后可得kp,ki,kd的模糊控制规则及其隶属函数分别如表2–4和图4所示.

表2 遗传算法优化后的kp规则库Table 2 kp rule library optimized by genetic algorithm

表3 遗传算法优化后的ki规则库Table 3 ki rule library optimized by genetic algorithm

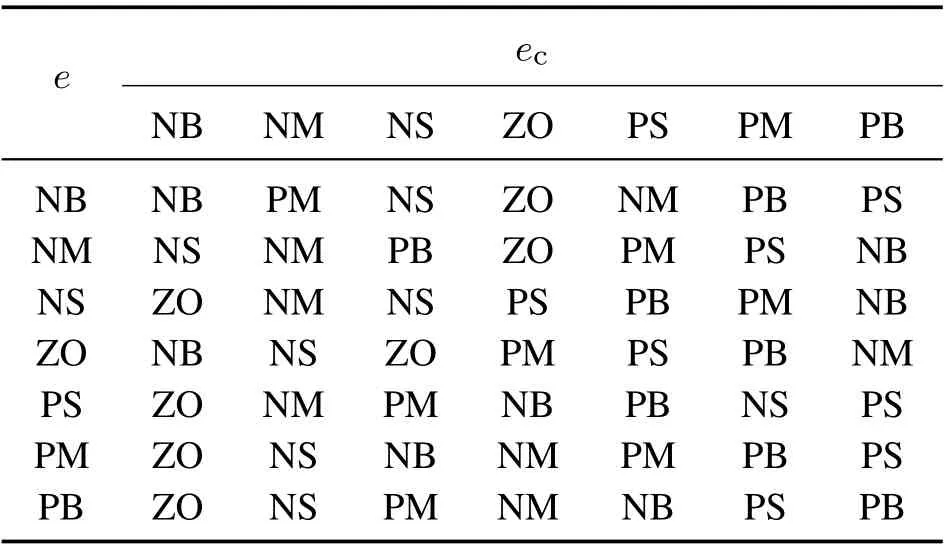
表4 遗传算法优化后的kd规则库Table 4 kd rule library optimized by genetic algorithm

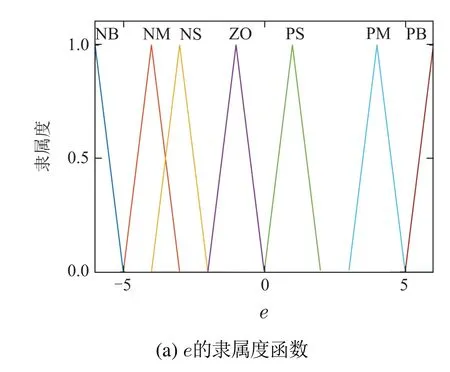
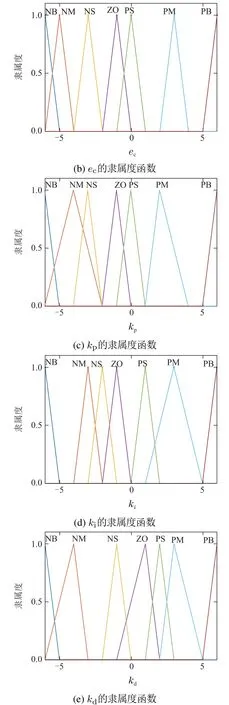
图4 遗传算法优化后的隶属函数Fig.4 Membership function optimized by genetic algorithm

在干扰状态下,高效的控制系统能快速响应系统的波动,同时拥有较高的控制精度,可用调节时间、上升时间、超调量和静态误差来描述.为了验证所提方法的优越性,本文在恒温水浴槽监控系统的基础上对系统温度进行控制,在同等条件下同时对比传统PID控制系统、模糊PID控制系统和所提方法的基于DDPG模糊自整定控制系统的响应曲线,结果如图5所示.

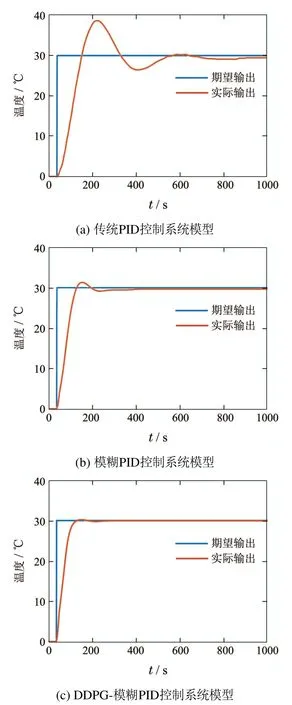
图5 目标温度为30◦C时3种模型算法动态响应曲线Fig.5 Dynamic response curves of three model algorithms when the target temperature is 30◦C

由图5可知,由于DDPG-模糊PID控制系统引入了DDPG辅助控制器,相比传统PID控制系统和模糊PID控制系统,DDPG-模糊PID控制系统有更低的调节时间和超调量,能够有效消除大滞后带来的系统不稳定的问题,且有效消除了系统的静态误差,使得系统的动态响应曲线能够准确的达到目标控制温度.

如表5所示,相比与模糊PID控制系统,DDPG-模糊PID控制系统能够有效解决温度控制系统的大延迟问题,调节时间提升了39.3%.大超调量容易对系统器件造成破坏,且有效降低系统的超调量,DDPG-模糊PID控制系统极大降低温度控制系统的超调量,超调量仅有0.68%,相比模糊PID系统,超调量性能提升99.7%,且系统的上升时间也明显加快.此外,DDPG-模糊PID控制系统的静态误差也有较大提升,仅有0.11◦C,相比模糊PID系统,提升了73.8%.

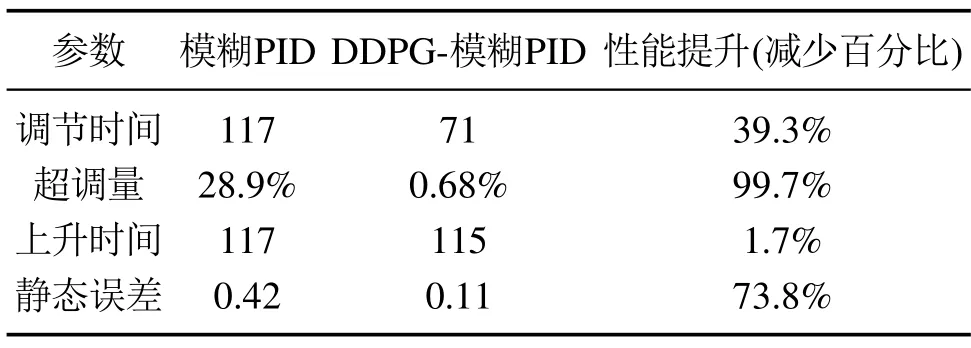
表5 测温30◦C的参数Table 5 Parameters for measuring temperature at 30◦C

由于系统电路中可能存在电磁干扰(传导干扰和辐射干扰),输入电压和传感器会给控制系统带来噪声干扰.因此,本文增加了噪声的实验,测试所提系统在加入白噪声情况下的动态响应.如图6所示,对温度调节系统加入白噪声干扰,传统的PID控制系统和模糊PID控制系统受白噪声影响较大,本文提出的DDPG-模糊PID控制系统利用DDPG算法进行在线权值学习能力,对系统执行器进行辅助控制有效抑制了白噪声干扰,使得输出相应曲线几乎不受噪声影响.

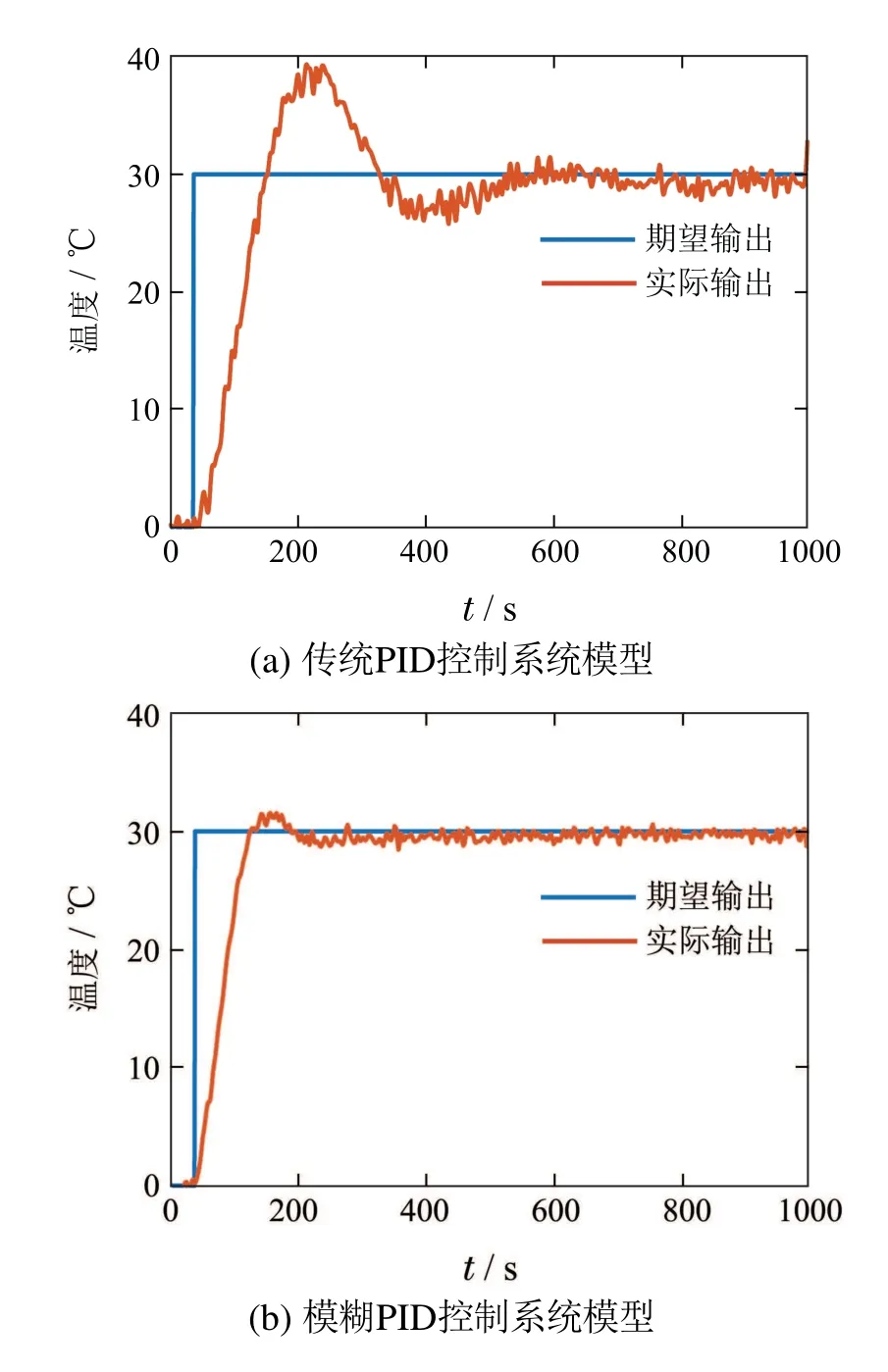
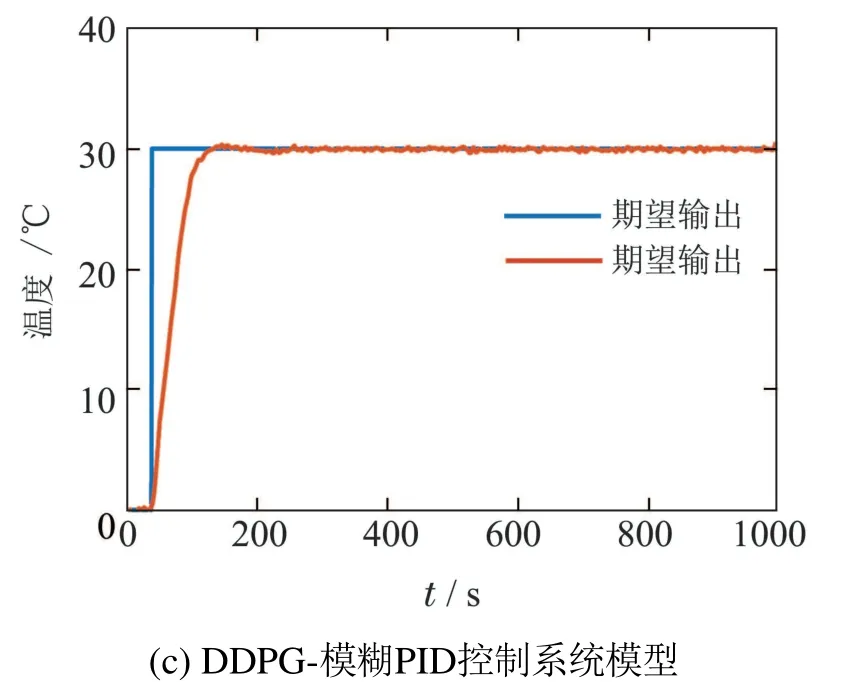
图6 白噪声干扰下目标温度为30◦C时3种模型算法动态响应曲线Fig.6 The dynamic response curves of the three model algorithms when the target temperature is 30◦C under the interference of white noise

6 结论

针对传统模糊PID温控系统响应慢、误差大、超调量高等问题,本文提出了深度确定性策略梯度与模糊PID的协同温度控制.此算法在模糊PID控制器的基础上,建立了以模糊PID为主控制器的温度调节系统,通过遗传算法筛选模糊PID的最优隶属函数和模糊规则.为了使系统实现快速响应、减少误差同时减小系统超调量,设计了一种新的基于DDPG的辅助控制器,利用DDPG算法进行在线权值学习能力,对系统执行器进行辅助控制,能够有效补偿温控系统的不确定性和干扰,通过主辅双控制器的联动控制,获得鲁棒的温度调控系统.实验结果表明,本文提出的双控制器温度调节系统对温度系统的调节鲁棒性要远优于传统温度控制系统,调节时间、延迟时间等都有明显缩短.因此,可以预见,本论文提出算法在控制领域将有极大的应用前景.