一类新的曲率积分不等式*

马磊，罗庆仙，徐镇猛

(广东茂名幼儿师范专科学校 理学院, 广东 茂名 525200)

1 文献综述及问题的提出

19世纪, 出于对部分物理现象和实际问题研究的需要, 几何学家们研究了曲线或曲面受不同外力的影响时曲率函数发展的相关问题。尤其, 针对沿曲线法线方向且以主曲率函数为速度的曲线的发展问题已引起了广泛的关注.Gage[1]在研究平面上一类保面积的曲率流的发展问题时, 得到了一个涉及平面凸曲线的曲率积分的不等式 (1)。目前，一般称此不等式为Gage等周不等式[2],具体表述如下；设∂K：(I→R2)为平面上边界光滑的紧致闭凸集K的边界曲线, 其曲率为κ, 面积及周长分别为A,L,则

(1)

20世纪,Green 与 Osher在[2]中推广了Gage的结果 (1),得到了一般形式的结果,其表达式形如

(2)

即曲率的幂积分的下界可以由曲线所围成的面积与其长度作为参数来估计.特别地,不等式 (2) 中n=2时,即为著名的Gage等周不等式；n=3，4时，其表达式分别为

这类不等式的新证明及推广参见文献[4,5,6,7,8],相关的应用参见文献[9,10,11]。

本文利用文献[12]中的分析形式的仿射等周不等式, 得到了一类分析形式的积分不等式并给出了其等号成立的条件。应用这类积分不等式应用我们得到了一类关于凹函数的曲率积分不等式, 这类曲率积分不等式的特殊形式为著名的曲率熵不等式(3)[3,8]与部分曲率的幂积分上界估计的不等式 (4)。

曲率熵不等式具体表述如下：设K为R2中边界为C2光滑的紧致闭凸集,则K的面积A,边界曲线∂K的相对曲率k满足不等式

(3)

当且仅当∂K为圆时等号成立。

(4)

等号成立当且仅当∂K为圆。

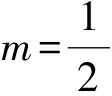
2 预备知识

在平面几何中, 关于支撑函数的理论部分可以参见经典的著作[14-16]。

平面R2中的直线G可以由垂直于G的方向与x轴的正方向的夹角θ以及原点到直线G的距离p=p(θ)决定.并且满足方程xcosθ+ysinθ-p(θ)=0.

(5)

当p=p(θ)随θ变化时,方程(5)为一族直线的方程, 且p=p(θ)是以2π为周期的连续函数。对直线族方程(5)两边同时关于θ求导可得

(6)

由方程 (5) 与 (6) 可得直线族的参数方程

x=-pcosθ+p′sinθ，y=-psinθ-p′cosθ.

(7)

如果直线族为紧致凸集K的边界∂K的包络, 则称p=p(θ)为凸集K的支撑函数(或凸曲线∂K的支撑函数)。

假设p=p(θ)是C2(二阶连续可微) 函数, 凸曲线∂K的弧长微元为ds,则由 (7) 可知,

(8)

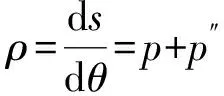
众所周知,以2π为周期的函数p=p(θ)为凸集K的支撑函数(或凸曲线∂K的支撑函数)的充要条件为ρ=p+p″>0(参见[14,15])。另外,当且仅当ρ为某一正常数时K的边界曲线∂K为圆,即当且仅当存在常数a,b,c使得p(θ)=acosθ+bsinθ+c时,K的边界曲线∂K为圆。若凸集K的支撑函数(或凸曲线∂K的支撑函数)是C2函数, 则凸集K的边界(凸曲线∂K)的相对曲率, 周长及其面积可分别为(参见[14,15,16])

(9)

(10)

(11)

3 定理及其证明

下面的结论(引理1)为仿射微分几何中分析形式的仿射等周不等式(参见[12]), 对证明本文的结论起着关键性的作用。

引理1设K为R2中边界为C2光滑的紧致闭凸集, 其支撑函数为p(θ), 则

(12)

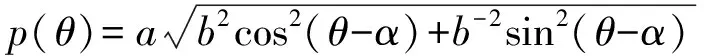
定理1 设K为R2中边界为C2光滑的紧致闭凸集, 其支撑函数为p(θ),φ(t)为(0，+∞)上单调递增的凹函数,则

(13)

当且仅当存在常数a,b,c使得p(θ)=acosθ+bsinθ+c时等号成立。

证明由于K是R2中边界为C2光滑的紧致闭凸集, 所以K的边界曲线∂K的相对曲率κ大于0(参见[14],[15]). 由 (9) 式可知p+p″>0.

因此, 当p+p″为某个固定的正常数c时, 则存在常数a,b使得

p(θ)=acosθ+bsinθ+c，

且此时

(14)

(15)

所以,

(16)

由于φ(t)为(0，+∞)上的凹函数, 根据Jensen不等式可知

(17)

等号成立当且仅当p+p″为常数。

因此, 当p+p″不是常值函数时, 根据Jensen不等式等号成立的条件可知, 不等式 (17) 无法取到等号. 故当p+p″为不是常数c时,

(18)

又因φ(t)为(0，+∞)上的增函数, 由不等式(12)可知

(19)

所以

综上可知，不等式(13)成立且当且仅当存在常数a,b,c使得p(θ)=acosθ+bsinθ+c时等号成立。

定理2'设K为R2中边界为C2光滑的紧致闭凸集,其面积A与边界曲线∂K的相对曲率κ，φ(t)为(0,+∞)上单调递增的凹函数, 则

(20)

当且仅当∂K为圆时等号成立。

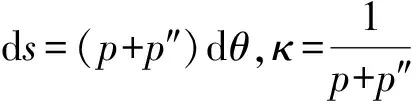
(21)

根据(11)式可得

(22)

由等式 (21), (22) , 结合定理1中的不等式 (13) 可知不等式 (20) 式成立, 且当且仅当∂Κ为圆时等号成立。

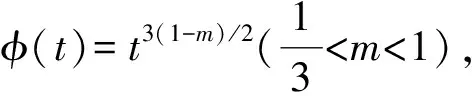
推论1 设K为R2中边界为C2光滑的紧致闭凸集，它的面积A与边界曲线∂K的相对曲率κ满足不等式

(23)

当且仅当∂K为圆时等号成立。

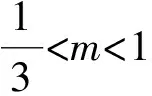
(24)

当且仅当∂Κ为圆时等号成立。

4 结语

本文利用分析形式的仿射等周不等式, 得到了一类新的积分不等式并给出了其等号成立的条件。作为这类积分不等式的直接应用, 得到了一类关于凹函数的曲率积分不等式, 这类曲率积分不等式的特殊形式为曲率熵不等式与一些特殊情况下曲率的幂积分上界估计的不等式。这种用分析的方法研究几何不等式的手段, 丰富了分析与几何的联系, 为研究曲率的幂积分的上下界估计提供了一种新的思路。