东海黑潮上下游不同的涡动能季节变化特征及其产生机制*
2022-03-25王思雯梁湘三赵宇慧王长友
王思雯 杨 洋 梁湘三 赵宇慧 王长友
东海黑潮上下游不同的涡动能季节变化特征及其产生机制*
王思雯1杨 洋1梁湘三2, 3①赵宇慧1王长友1
(1. 南京信息工程大学海洋科学学院 江苏南京 210044; 2. 复旦大学大气与海洋科学系以及大气科学研究院 上海 200438; 3. 上海期智研究院 上海 200232)
用一种新的泛函工具——多尺度子空间变换(multiscale window transform, MWT),得到如实的东海涡动能分布, 发现东海黑潮上下游区域的涡动能有着完全不同的季节变化特征。根据功率谱分析, 东海黑潮流系可正交地重构到背景流尺度子空间(大于64 d)与涡旋尺度子空间(小于64 d), 并用MWT得出相应子空间的能量, 后者即为涡动能。结果表明, 上游涡动能在8月达到峰值, 冬季最弱; 而下游涡动能在4月和9月存在两个峰值, 冬季最弱。利用基于MWT的正则传输理论以及局地多尺度能量分析方法, 发现正压不稳定和斜压不稳定是东海黑潮涡动能的主要来源, 且这两个来源决定了其上下游不同的季节变化。其中上游涡动能的季节变化主要受正压不稳定路径(即背景流动能向涡动能的正则传输)控制, 而下游涡动能在4月的峰值主要由斜压不稳定路径(即背景流有效位能向涡旋有效位能作正则传输并进一步转化为涡动能)决定, 其在9月的峰值受到正压不稳定和斜压不稳定的共同影响。
黑潮; 东海; 多尺度子空间变换; 正则传输; 正压不稳定; 斜压不稳定
黑潮是北太平洋副热带海区的一支强西边界流, 它起源于菲律宾东部海域, 经台湾和与那国岛之间的通道进入中国东海并沿东海大陆架向东北流动, 后经吐噶喇海峡流出东海进入日本南部海域, 最终向东汇入北太平洋(图1)。由于黑潮源源不断地将热量和营养物自南向北输送, 其流量和能量等的时空变化对西北太平洋区域的水文、渔业和气候有着深远的影响(Qiu, 2001; Matsuno, 2009)。黑潮主段位于东海, 流经区域存在大量中尺度和亚中尺度涡旋。这些涡旋大多集中在黑潮主轴, 沿主轴向东北方向传播(Liu, 2012; Qin, 2015; Cheng, 2017)。研究表明, 东海黑潮区域的涡旋一部分来自西北太平洋。在西北太平洋区域, 副热带逆流的斜压不稳定产生大量涡旋(Gill, 1974; Qiu, 1999; Roemmich, 2001; Qiu, 2010)。这些涡旋向西传播, 大部分会到达西北太平洋大陆坡附近(Yang, 1999; Zhang, 2001; Jan, 2017), 随后进入东海并对黑潮造成直接或间接的影响(Ichikawa, 1993; Andres, 2013; 王兴智等, 2014; Soeyanto, 2014; Jan, 2017)。而Cheng等(2017)指出琉球群岛岛链的存在使得很多涡旋很难进入东海, 故外来涡旋对东海黑潮附近的涡旋活动贡献不大, 并非该区域涡旋的主要来源。
东海黑潮区域大部分涡旋是局地产生的, 且呈现波状结构(郭炳火等, 1995)。大量研究均表明黑潮会通过失稳过程给涡旋的生成和发展提供能量(Wang, 1987; Jia, 2005; Yan, 2019)。Kamidaira等(2017)利用一个双重嵌套结构的海洋模式发现东海黑潮东北段以斜压不稳定的方式为涡旋提供能量。杨洋等(2019)使用一种新的多尺度能量分析方法指出东海黑潮上游表现为混合不稳定(即正压与斜压不稳定), 而下游则仅表现为斜压失稳。以上研究表明失稳过程在黑潮的上、下游是以不同方式表现出来的。

图1 研究区域地形图
注: 白色等值线代表基于混合坐标海洋模式(hybrid coordinate ocean model, HYCOM)再分析数据得到的平均海平面高度, 图中仅画出0, 0.1, 0.2 m的等值线, 用来表示黑潮流轴; 蓝色实线框代表本文重点关注区域; 数据来自ETOPO1
作为涡旋能量的主要来源, 东海黑潮的时空变化必然会对涡旋活动产生重要影响。大量的资料分析表明, 东海黑潮流速和流量均存在着显著的季节变化(袁耀初等, 2006)。总体来看, 东海黑潮流速夏季大、冬季小(Ichikawa, 1993; Li, 2020; 邓丽静等, 2014); 具体到上游与下游区域, 东海黑潮上游的流量呈现夏强秋弱的季节变化(Lee, 2007; Liu, 2012), 下游流量则存在夏强冬弱的季节特征(Yang, 2003)。东海黑潮的这种季节变化很有可能通过不稳定过程对涡旋活动进行调制。实际上, 目前在黑潮延伸体和南极绕极流区域已有很多研究证实背景流通过正压与斜压失稳等过程影响区域涡旋动能的季节变化(Qiu, 1999; Ebuchi, 2000; Phillips, 2000; Imawaki, 2001; Penduff, 2004; Andres, 2008; Chen, 2014)。那么东海黑潮涡动能的季节变化主要是受何种机制控制?上下游是否存在空间差异性?这些问题尚待研究。
本文将聚焦东海黑潮涡动能的季节变化, 并通过诊断涡动能收支方程, 探讨东海黑潮涡旋季节变化的成因。为了定量给出背景流和涡旋场之间的能量交换及其他能量输运过程, 本文将采用一种新的泛函分析工具, 即多尺度子空间变换(multiscale window transform, MWT; Liang, 2007b), 将东海黑潮重构至背景流尺度子空间和涡旋尺度子空间, 并采用基于MWT的正则传输理论和局地多尺度能量分析方法(Liang, 2005; Liang, 2016)对相关的多尺度能量过程进行诊断。有关该系列方法的介绍将在第2节给出。在第3节中, 我们将介绍本研究使用的数据。第4节展示了本研究的结果。第5节为本研究的主要结论。
1 方法
1.1 多尺度子空间变换(MWT)

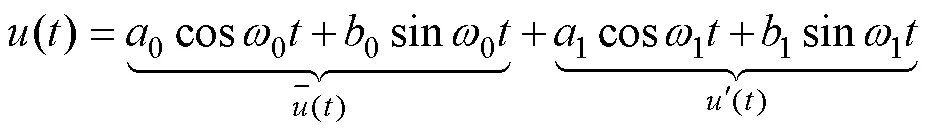



简单来说, MWT是一种泛函工具, 它将函数空间正交地分解成多个子空间的直和, 我们将这样的子空间称为尺度子空间(scale window), 或者简称子空间; 类似小波变换, MWT还具有局地性(因本研究讨论的是时间尺度, 这里的局地性即反映了时变信息)。需要强调的是, 这里正交性很重要, 否则Parseval等式无法成立, 从而物理意义上的能量无法被定义。Liang等(2007b)发现, 对于一类特殊的正交滤波器存在着与傅里叶变换与逆傅里叶变换类似的“变换-重构对”, 这种变换-重构对即MWT和多尺度子空间重构(multiscale window reconstruction; MWR)。对一个时间序列, 可以通过MWR得到相应的滤波场(重构场)。与一般滤波器不同的是, 这里还可以得到与之对应的MWT变换系数, Liang等(2007b)证明了重构场的能量等于变换系数的平方(再乘上一常系数)。更多细节和推导请参阅原文, 一个稍详尽的简介参见Liang (2016)。

1.2 正则传输
在能量学中, 要定量研究流体不稳定过程及其相关的多尺度相互作用(如涡流相互作用), 首先要得到正确的不同尺度间的能量传输项。在MWT的框架下, Liang (2016)提出了正则传输理论(canonical transfer)。假设在不可压的流场中, 有一标量场, 其随时间的变化如式(3)所示:

注:蓝线代表基于HYCOM再分析数据得到的表层流场动能谱; 橙线代表基于HYCOM再分析数据得到的深层700 m流场动能谱; 黄线代表基于AVISO观测数据得到的表层流场动能谱

图3 海表面高度及流速场的多尺度子空间变换重构
注:黑色箭头为流速场(单位:m/s); a、c、e为1994年7月4日; b、d、f为2011年5月21日; a和b为原始场; c和d为平均流场; e和f为涡旋场; 数据来自HYCOM



且上述传输项满足守恒定律:

为了比较传统方法中的能量传输与正则传输的区别, 我们将二者的能量方程都基于雷诺分解(即分成平均场和扰动场两个尺度)导出。在传统方法(如Von Storch, 2012; Yan, 2019)中, 平均场和扰动场的能量方程具有如下形式
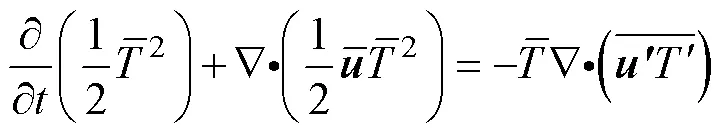

这里, 如果是速度场, 那么此两式是平均场和扰动场的动能方程; 如果是密度异常场, 那么此两式对应有效位能方程。为了简便起见这里只列出了跨尺度传输和空间输运项, 因为传统方法和本文所用方法最根本的区别体现在这两类过程。等式左边具有散度形式的项为输运项, 等式右边则为传统方法中的跨尺度传输项, 我们注意到,


由于雷诺分解是MWT的一种特殊情形, Liang等(2007b)得到了雷诺分解下的正则传输, 相应的能量方程有如下形式:


表1 基于雷诺分解的传统传输和正则传输项的数学表达式

Tab.1 Mathematical expressions of the traditional transfer and canonical transfer based on Reynolds decomposition
1.3 局地多尺度能量分析
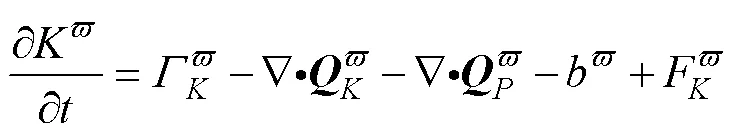

2 数据
本研究采用HYCOM模式输出的再分析数据, 版本号为GLBv0.08 (https://www.hycom.org/dataserver/ gofs-3pt1/reanalysis)。HYCOM是基于原始方程发展出来的全球海洋环流模式, 它不仅保留了等密度坐标海洋模式等密度面坐标的优点, 还采用垂向混合坐标(等密度坐标、地形跟随坐标和垂直坐标), 弥补了等密度面坐标的不足(Chassignet, 2007)。HYCOM在东海黑潮区域的输出数据具有0.08°的空间分辨率; 垂直方向分为40层, 由表层的0 m逐渐扩大到最大深度5 000 m。本研究采用的是时间分辨率为1 d的温盐场和流速场, 时间跨度为1994~2015年。为了验证模式数据的准确性以及子空间尺度分离界限的合理性, 本文还采用了AVISO (Archiving Validation and Interpretation of Satellite Oceanographic)数据中心提供的海平面高度数据和海表地转流速场数据, 该数据是多个卫星高度计数据融合的产品, 其时间长度为1994~2015年, 时间分辨率为1 d, 空间分辨率为1/4°。
表2 式(12)和式(13)中能量项的数学表达式和物理解释

Tab.2 Mathematical expressions and meanings of the energetics terms in equations (12) and (13)
注: “:”为并矢算符, 如: (): ()=()(), 详见Liang (2016)
3 结果分析
3.1 东海黑潮涡动能的季节变化
本节将基于HYCOM模式数据探究东海黑潮海域涡动能的季节变化特征。在此之前, 我们首先验证HYCOM模式数据的准确性。图4所示为分别采用AVISO观测资料和HYCOM模式输出资料计算得到的1994~2015年东海黑潮区域表层涡动能气候态水平分布图, 黑色方框标注了东海黑潮主轴的大致范围, 为本文重点关注区域。观测(图4a)表明黑潮主轴区域涡动能较强, 尤其在靠近吐噶喇海峡区域处有一涡动能大值中心; 模式数据(图4b)对涡动能的这一空间分布有较好地再现。对选定区域内的涡动能进行空间平均, 我们得到了图5所示的表层涡动能年循环变化。从卫星观测可知, 东海黑潮主轴区域涡动能存在明显的春强冬弱的季节变化(图5橙色折线)。这一季节变化也被HYCOM模式输出资料准确反映出来(图5蓝色折线)。需要注意的是, 相比于观测, 基于HYCOM数据计算得到的表层涡动能幅值较大, 造成这种差异的主要原因是数值模式较卫星观测具有更高的空间分辨率, 使得模式中的涡动能整体偏强(Sasaki, 2017; Yang, 2017)。综上, HYCOM模式数据较好地再现了东海黑潮区域涡动能的时空变化, 对于我们探究该区域涡动能季节变化来说是可靠的。

图4 1994~2015年平均表层涡动能空间分布
注:黑色实线框代表本文重点关注区域, 余同

图5 东海黑潮主轴区域表层涡动能逐月变化
注: 蓝色折线基于HYCOM再分析数据; 橙色折线基于AVISO观测数据
图6展示了涡动能异常(即涡动能减去其时间平均值)进行垂直积分(0~1 000 m)后得到的逐月水平分布。从图6可见, 东海黑潮区域涡动能季节存在显著的季节变化, 且季节信号主要集中在黑潮主轴, 总体表现为春季涡动能最强, 冬季最弱。有趣的是, 从图6涡动能异常的空间分布可见, 黑潮在东海区域的上游和下游呈现明显不同的季节变化。具体来说, 上游的涡动能8月最强、1月最弱, 下游涡动能在4月和9月均有峰值, 在1月左右达到谷值。如图7所示, 上述这种上、下游涡动能季节变化的差异在垂直方向上的表现也是一致的。据此, 我们将东海黑潮区域分为上、下游两个子区域, 两个区域的空间范围如图6中的绿色框线所标注。图8a和8b给出了这两个子区域平均涡动能的逐月变化。由图8a和8b可以清楚地看到, 东海黑潮上游的涡动能从1月开始增加, 到8月达到峰值, 而后开始迅速减小; 而在东海黑潮下游, 涡动能的季节变化整体呈马鞍形分布, 其在4月和9月分别有一个峰值, 后者略小于前者, 与上游类似, 11月、12月和1月是下游涡动能最弱的3个月。
综上, 我们基于HYCOM模式数据发现东海黑潮区域涡动能存在显著的季节变化, 且这种季节变化在黑潮上、下游两个子区域并非是同步的。其中, 东海黑潮上游的涡动能在8月出现峰值, 冬季月份最弱; 下游涡动能则在4月和9月出现两个峰值, 且4月的峰值更大, 冬季月份最弱。从东海黑潮主轴附近的密度分布(图7)来看, 黑潮上游等密线较为平直, 下游则有明显倾斜, 尤其是在下游涡动能最强的4月。这说明相较上游, 东海黑潮下游具有更强的斜压性, 这很有可能是导致东海黑潮上、下游涡动能季节变化不同步的原因之一。接下来, 我们将基于局地多尺度能量分析, 对包括斜压不稳定在内的相关能量过程进行诊断和分析, 阐明东海黑潮涡动能季节变化背后的成因。
3.2 东海黑潮涡动能的来源
在探究控制东海黑潮涡动能季节变化的主要原因之前, 我们首先对能量收支方程的各项进行诊断, 给出该区域涡动能的主要来源。需要注意的是, 本研究所用的有效位能的定义基于准地转假设, 该定义在密度层结较弱的混合层不适用(杨洋等, 2019)。为了使诊断结果更加准确, 后续研究中对相关能量项的垂直积分只考虑50 m以深的水柱。注意这一垂直积分范围的减小并不影响我们在3.1中得到的结论。图8a和8b分别给出了0~1 000 m和50~1 000 m垂直积分的区域平均涡动能变化, 可以清楚地看到这两个范围内的垂直积分的涡动能季节变化是完全一致的。


图6 0~1 000 m积分的涡动能异常的逐月空间分布
注:黑色箭头为表层流速场; 绿色实线框代表本文重点关注区域
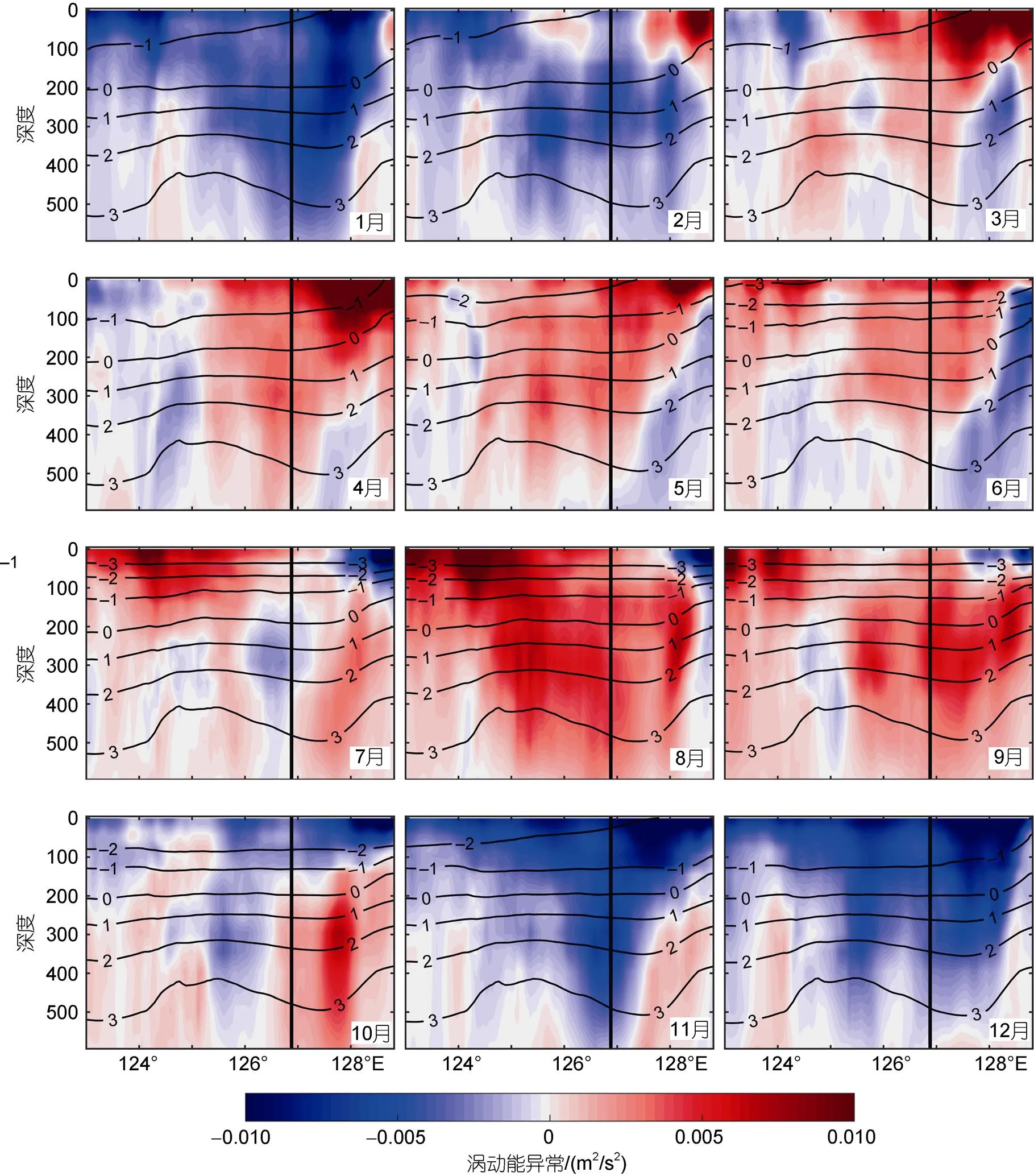
图7 沿黑潮流轴的涡动能异常的逐月截面图
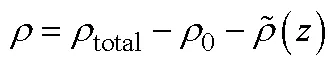

图8 东海黑潮上游(a)和下游(b)区域涡动能垂直积分逐月变化
注: 红线表示0~1 000 m垂直积分, 蓝线表示50~1 000 m垂直积分; 数据来自HYCOM
Yan等(2019)利用OFES (the ocean general circulation model for the earth simulator)模式数据对西北太平洋海域涡-流能量学做了分析, 其结果显示正压传输在东海黑潮主轴以西以EKE→MKE为主, 主轴以东以MKE→EKE, 斜压传输主要集中在下游, 但具有明显正负相间的空间分布。这些与本文的结果非常不同, 我们发现这种差异与所用的不同方法和不同数据均有关系。图10给出了传统方法和正则传输理论中的正压传输和斜压传输在雷诺分解下的水平分布(数学表达式如表1所示)。通过比较图10a, 10b与图10c, 10d, 我们可以看到基于MWT分离(即以64 d为截断周期分离背景场和涡动场)与雷诺分解(即将原始场分离为时间平均和扰动场)得到的正则传输具有大体一致的空间分布。不过相比MWT的64 d尺度分离, 雷诺分解框架下的正则传输振幅更强, 这应该与雷诺分解下的涡动场包含了所有时间尺度的扰动有关。比较图10c, 10d与图10e, 图f, 则可以看到基于雷诺分解的传统斜压传输与斜压正则传输大致呈现相近的空间分布, 但正则斜压传输在下游的强度要明显大于传统的斜压传输。相比于斜压传输, 两种方法下的正压传输空间差异较明显, 传统的正压传输正值主要集中在东海黑潮主轴右侧(图10e), 这与Yan等的结果类似, 而正则正压传输正值沿主轴中心分布, 在下游则有明显的负值区域。以上结果表明两种方法得到的跨尺度能量传输会有明显差异, 尤其是正压传输。同时我们发现, Yan等(2019)根据OFES数据得到的正压传输沿主轴东正西负的结构在HYCOM数据计算得到的结果中却没有体现出来, 说明不同数据也会导致结果有较大差异。
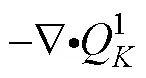
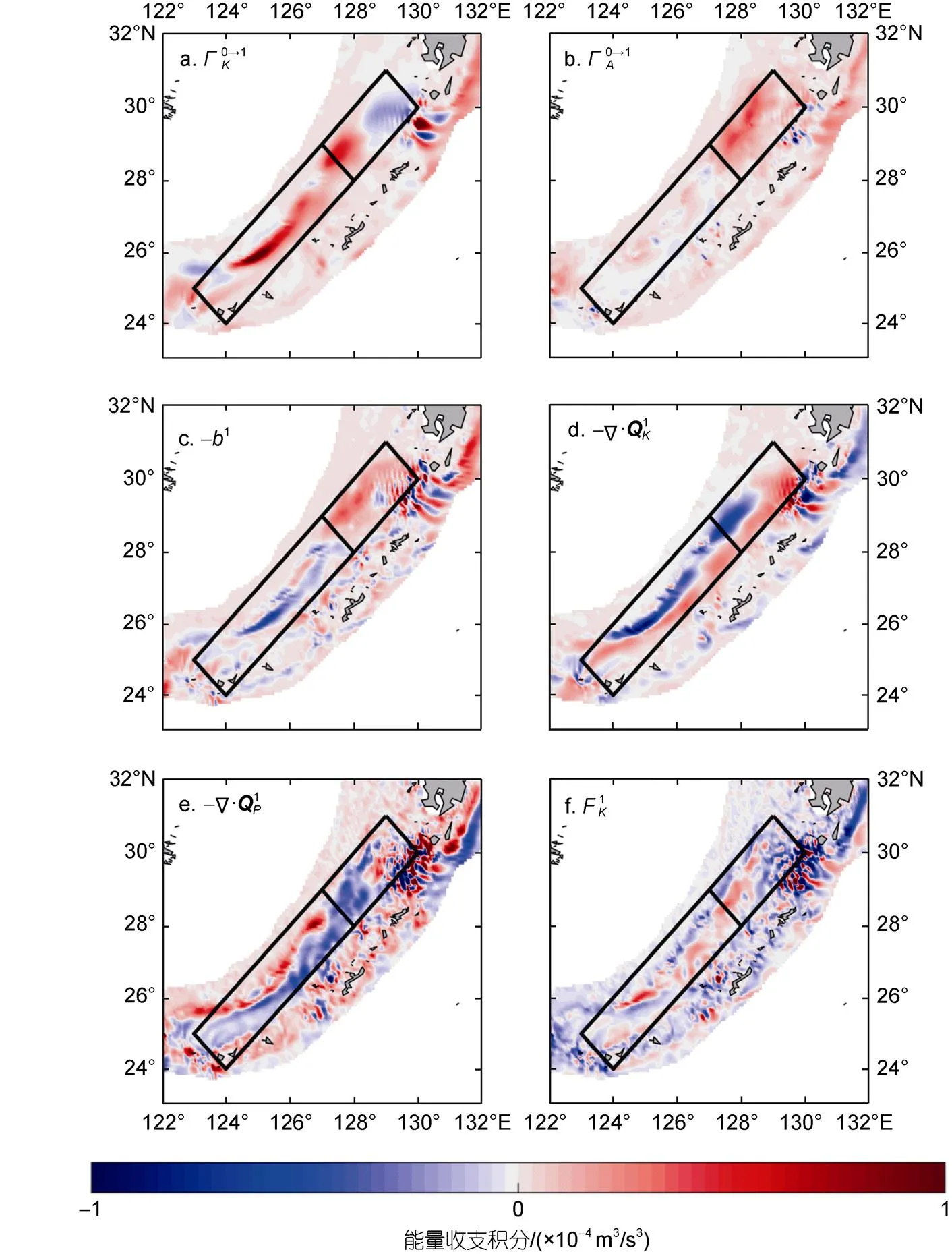
图9 能量收支各项在50~1 000 m垂直积分的气候态空间分布
表3 各能量收支项在上游和下游区域的气候态平均值

Tab.3 The area-mean energy budget terms in the upstream and downstream regions of the Kuroshio in the East China Sea
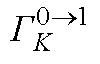
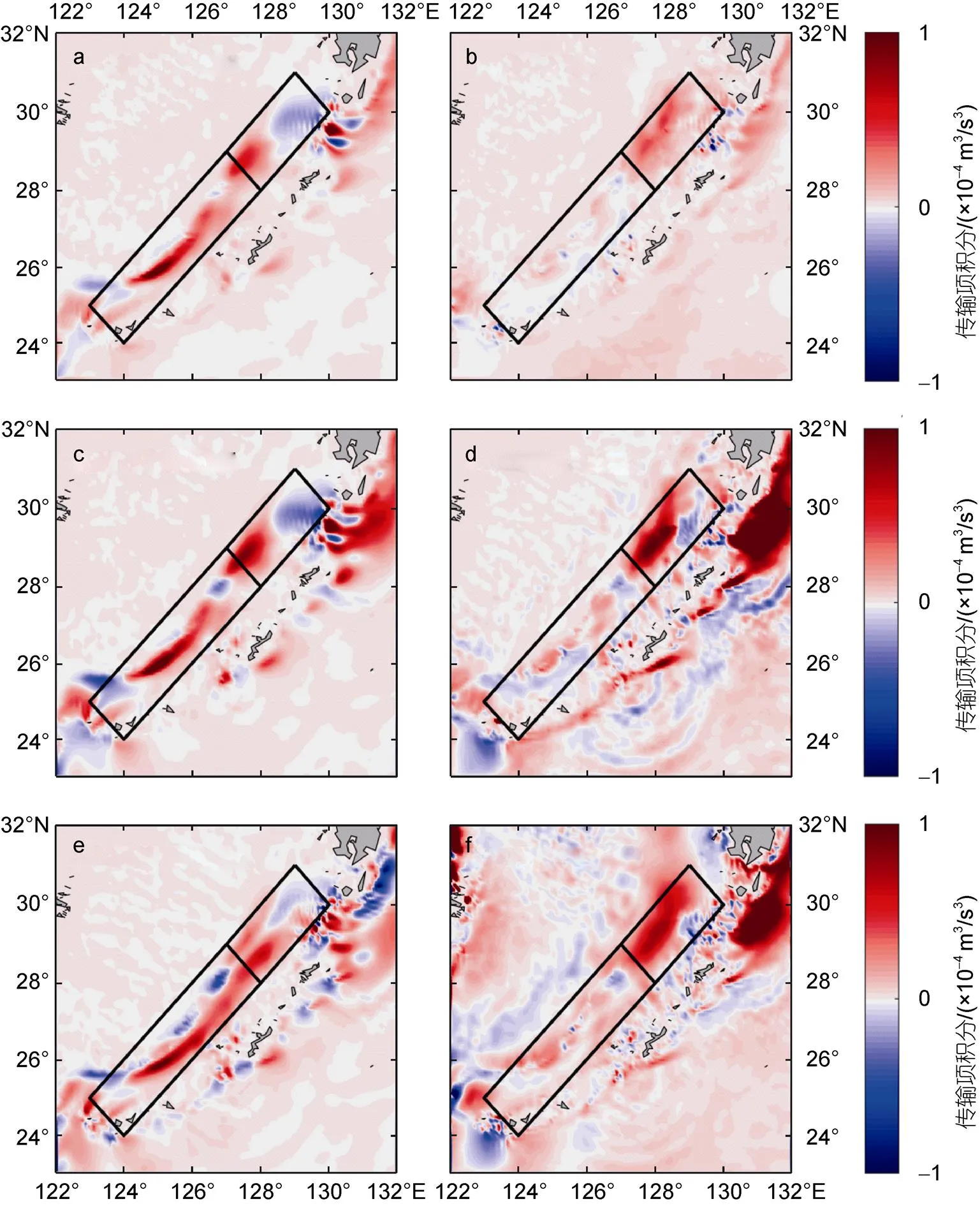
图10 传统传输项和正则传输项在50~1 000 m垂直积分的气候态空间分布
注: a和b: 以64 d为截断周期所得的正则传输项; c和d: 基于雷诺平均所得的扰动场与平均场之间的正则能量传输; e和f: 基于雷诺平均所得的扰动场与平均场之间的传统能量传输; 左侧一列均为正压传输, 右侧一列均为斜压传输; 数据来自HYCOM
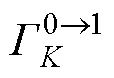
3.3 东海黑潮涡动能季节变化形成机制
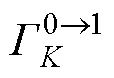

图11 50~1 000 m垂直积分的能量收支各项在上下游的逐月变化

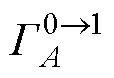

图12 50~1 000 m垂直积分的正则传输项及浮力转换项在下游的逐月变化

综上所述, 控制东海黑潮流域上下游涡动能季节变化的机制具有显著差异。上游涡动能在8月达到峰值, 受正压不稳定控制。下游涡动能年循环有两个峰值, 一个在4月, 另一个在9月。其中4月的峰值受斜压不稳定控制, 而9月的峰值则受正压不稳定和斜压不稳定共同影响。
4 结论
利用1/12.5°分辨率的HYCOM再分析数据, 本文探究了东海黑潮区域涡动能的季节变化及其动力机制。我们首先利用一个为新的泛函工具——多尺度子空间变换(MWT; Liang, 2007a), 将东海黑潮流系正交地重构到两个尺度子空间:背景流尺度子空间(大于64 d)与涡旋尺度子空间(小于64 d)。由于MWT的正交性和局地性使得我们能够进一步研究涡旋尺度子空间的动能(EKE)的时变特征。结果表明, 东海黑潮区域的涡动能存在明显的季节变化, 且在东海黑潮上、下游表现出空间差异:上游涡动能水平整体较弱, 在8月达到峰值, 冬季最弱; 下游涡动能水平整体较强, 除了在9月有一峰值外, 另一个更强的峰值出现在4月。
随后, 我们使用一套基于MWT的正则传输理论以及局地多尺度能量收支方程(Liang, 2016)进一步研究影响东海黑潮上下游涡动能季节变化的原因。与传统能量方程中的传输过程不同, 正则传输可以信实地表征流体运动中不同尺度之间的能量交换, 因而可以信实地诊断出流体内部的不稳定过程(Liang, 2007a)。通过诊断东海黑潮流域涡动能收支方程, 我们发现与正压不稳定相关的正压能量路径(MKE→EKE)和与斜压不稳定相关联的斜压能量路径(MAPE→EAPE→EKE)是东海黑潮EKE的主要来源, 且从气候平均角度来看这两种能量路径在黑潮上下游存在一种跷跷板现象:上游以正压能量路径为主, 斜压能量路径受到明显抑制, EKE反而向EAPE转换; 下游以斜压能量路径为主, 吐噶喇海峡西侧有一片区域EKE反向MKE级串, 使得下游正压能量路径的区域平均值较低。从各能量过程的季节演变上来看, 在东海黑潮上游, MKE→EKE在8月最强, 冬季月份最弱, 与上游的EKE季节变化一致。而上游区域的MAPE→EAPE和EAPE→EKE很弱, 尤其在夏季EAPE反而向MAPE级串, EKE向EAPE转换。与上游不同的是, 东海黑潮下游的斜压能量路径在4月达到最强, 对应该月的EKE峰值。而在9月, 虽然MAPE→EAPE有一峰值, 但EAPE在同期没有显著地向EKE转换, 说明单纯靠斜压能量路径不足以使EKE在9月达到极值, 这个EKE极值被证明与正压能量路径有关。
本文揭示了东海黑潮上下游涡动能的季节变化机制截然不同, 主要表现在与涡流相互作用有关的正压不稳定和斜压不稳定过程在上下游区域存在明显差异。这说明在研究东海黑潮涡旋动力学时, 有必要对上下游进行分段考察。比如在搭建针对该海域的数值模式时, 黑潮的正压(斜压)不稳定过程是准确模拟上游(下游)涡旋季节变化的关键。换言之, 东海黑潮海域涡旋在季节尺度上的预报能力取决于模式能否准确模拟这两个关键性的内部动力过程。此外, 由于HYCOM再分析数据分辨率的限制, 本文所讨论的涡动能主要是中尺度过程(如黑潮锋面涡、锋面弯曲等)相关联的动能, 不包含亚中尺度过程。亚中尺度动能已被观测和高分辨率模式证实具有显著的季节变化。最近有一些研究表明, 亚中尺度过程可以通过能量逆级串的形式影响中尺度过程动能的季节变化(Qiu, 2014; Sasaki, 2014)。亚中尺度过程对黑潮涡动能季节变化具有怎么样的影响?其动力学机制如何?这些都是值得进一步讨论的科学问题。今后, 我们将借助更高分辨率的模式来探讨上述问题。
王兴智, 李崇银, 王桂华, 2014. 东海黑潮活跃区表层流场的半年内时间尺度变化研究[J]. 海洋学报, 36(11): 1-11.
邓丽静, 魏皓, 汪嘉宁, 2014. PN断面黑潮流速垂直分布特征及机制分析[J]. 海洋通报, 33(5): 519-526.
杨洋, 梁湘三, 2019. 黑潮流域内在的平均流-低频变率-中尺度涡之间的非线性相互作用[J]. 中国科学: 地球科学, 49(3): 596-610.
袁耀初, 杨成浩, 王彰贵, 2006. 2000年东海黑潮和琉球群岛以东海流的变异Ⅰ. 东海黑潮及其附近中尺度涡的变异[J]. 海洋学报, 28(2): 1-13.
郭炳火, 汤毓祥, 陆赛英, 等, 1995. 春季东海黑潮锋面涡旋的观测与分析[J]. 海洋学报, 17(1): 13-23.
ANDRES M, CENEDESE C, 2013. Laboratory experiments and observations of cyclonic and anticyclonic eddies impinging on an island [J]. Journal of Geophysical Research: Oceans, 118(2): 762-773.
ANDRES M, PARK J H, WIMBUSH M,, 2008. Study of the Kuroshio/Ryukyu Current system based on satellite-altimeter and in situ measurements [J]. Journal of Oceanography, 64(6): 937-950.
CHASSIGNET E P, HURLBURT H E, SMEDSTAD O M,, 2007. The HYCOM (hybrid coordinate ocean model) data assimilative system [J]. Journal of Marine Systems, 65(1/4): 60-83.
CHEN R, FLIERL G R, WUNSCH C, 2014. A description of local and nonlocal eddy–mean flow interaction in a global eddy-permitting state estimate [J]. Journal of Physical Oceanography, 44(9): 2336-2352.
CHEN R, THOMPSON A F, FLIERL G R, 2016. Time-dependent eddy-mean energy diagrams and their application to the ocean [J]. Journal of Physical Oceanography, 46(9): 2827-2850.
CHENG Y H, HO C R, ZHENG Q N,, 2017. Statistical features of eddies approaching the Kuroshio east of Taiwan Island and Luzon Island [J]. Journal of Oceanography, 73(4): 427-438.
EBUCHI N, HANAWA K, 2000. Mesoscale eddies observed by TOLEX-ADCP and TOPEX/POSEIDON altimeter in the Kuroshio recirculation region south of Japan [J]. Journal of Oceanography, 56(1): 43-57.
GILL A E, GREEN J S A, SIMMONS A J, 1974. Energy partition in the large-scale ocean circulation and the production of mid-ocean eddies [J]. Deep Sea Research and Oceanographic Abstracts, 21(7): 499-528, IN1, 509-528.
HOLOPAINEN E O, 1978. A diagnostic study on the kinetic energy balance of the long-term mean flow and the associated transient fluctuations in the atmosphere [J]. Geophysica, 15: 125-145.
ICHIKAWA H, BEARDSLEY R C, 1993. Temporal and spatial variability of volume transport of the Kuroshio in the East China Sea [J]. Deep Sea Research Part I: Oceanographic Research Papers, 40(3): 583-605.
IMAWAKI S, UCHIDA H, ICHIKAWA H,, 2001. Satellite altimeter monitoring the Kuroshio transport south of Japan [J]. Geophysical Research Letters, 28(1): 17-20.
JAN S, MENSAH V, ANDRES M,, 2017. Eddy-Kuroshio interactions: local and remote effects [J]. Journal of Geophysical Research: Oceans, 122(12): 9744-9764.
JIA Y L, LIU Q Y, LIU W, 2005. Primary study of the mechanism of eddy shedding from the Kuroshio bend in Luzon Strait [J]. Journal of Oceanography, 61(6): 1017-1027.
KAMIDAIRA Y, UCHIYAMA Y, MITARAI S, 2017. Eddy-induced transport of the Kuroshio warm water around the Ryukyu Islands in the East China Sea [J]. Continental Shelf Research, 143: 206-218.
LEE J S, TAKESHI M, 2007. Intrusion of Kuroshio water onto the continental shelf of the East China Sea [J]. Journal of Oceanography, 63(2): 309-325.
LI P, SHI B W, LI Y G,, 2020. Characterization of longshore currents in southern East China Sea during summer and autumn [J]. Acta Oceanologica Sinica, 39(3): 1-11.
LIANG X S, 2016. Canonical transfer and multiscale energetics for primitive and quasigeostrophic atmospheres [J]. Journal of the Atmospheric Sciences, 73(11): 4439-4468.
LIANG X S, ANDERSON D G M, 2007a. Multiscale window transform [J]. Multiscale Modeling & Simulation, 6(2): 437-467.
LIANG X S, ROBINSON A R, 2005. Localized multiscale energy and vorticity analysis: I. Fundamentals [J]. Dynamics of Atmospheres and Oceans, 38(3/4): 195-230.
LIANG X S, ROBINSON A R, 2007b. Localized multi-scale energy and vorticity analysis: II. Finite-amplitude instability theory and validation [J]. Dynamics of Atmospheres and Oceans, 44(2): 51-76.
LIU Z Q, GAN J P, 2012. Variability of the Kuroshio in the East China Sea derived from satellite altimetry data [J]. Deep Sea Research Part I: Oceanographic Research Papers, 59: 25-36.
MATSUNO T, LEE J S, YANAO S, 2009. The Kuroshio exchange with the South and East China seas [J]. Ocean Science, 5(3): 303-312.
PENDUFF T, BARNIER B, DEWAR W K,, 2004. Dynamical response of the oceanic eddy field to the North Atlantic Oscillation: a model–data comparison [J]. Journal of Physical Oceanography, 34(12): 2615-2629.
PHILLIPS H E, RINTOUL S R, 2000. Eddy variability and energetics from direct current measurements in the Antarctic Circumpolar Current South of Australia [J]. Journal of Physical Oceanography, 30(12): 3050-3076.
PLUMB R A, 1983. A new look at the energy cycle [J]. Journal of Atmospheric Sciences, 40(7): 1669-1688.
QIN D D, WANG J H, LIU Y,, 2015. Eddy analysis in the Eastern China Sea using altimetry data [J]. Frontiers of Earth Science, 9(4): 709-721.
QIU B, 1999. Seasonal eddy field modulation of the North Pacific Subtropical Countercurrent: TOPEX/Poseidon observations and theory [J]. Journal of Physical Oceanography, 29(10): 2471-2486.
QIU B, 2001. Kuroshio and Oyashio currents [M] // STEELE J H. Encyclopedia of Ocean Sciences. San Diego, CA, USA: Academic Press: 1413-1425.
QIU B, CHEN S M, 2010. Interannual-to-decadal variability in the bifurcation of the North Equatorial Current off the Philippines [J]. Journal of Physical Oceanography, 40(11): 2525-2538.
QIU B, CHEN S M, KLEIN P,, 2014. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent [J]. Journal of Physical Oceanography, 44(12): 3079-3098.
ROEMMICH D, GILSON J, 2001. Eddy transport of heat and thermocline waters in the North Pacific: a key to interannual/decadal climate variability? [J]. Journal of Physical Oceanography, 31(3): 675-687.
SASAKI H, KLEIN P, QIU B,, 2014. Impact of oceanic-scale interactions on the seasonal modulation of ocean dynamics by the atmosphere [J]. Nature Communications, 5(1): 5636.
SASAKI H, KLEIN P, SASAI Y,, 2017. Regionality and seasonality of submesoscale and mesoscale turbulence in the North Pacific Ocean [J]. Ocean Dynamics, 67(9): 1195-1216.
SOEYANTO E, GUO X Y, ONO J,, 2014. Interannual variations of Kuroshio transport in the East China Sea and its relation to the Pacific Decadal Oscillation and mesoscale eddies [J]. Journal of Geophysical Research: Oceans, 119(6): 3595-3616.
VON STORCH J S, EDEN C, FAST I,, 2012. An estimate of the Lorenz energy cycle for the world ocean based on the 1/10° STORM/NCEP simulation [J]. Journal of Physical Oceanography, 42(12): 2185-2205.
WANG W, SU J L, 1987. A barotropic model of the Kuroshio system and eddy phenomena in the East China Sea [J]. Acta Oceanologica Sinica, 6(S1): 21-35.
YAN X M, KANG D J, CURCHITSER E N,, 2019. Energetics of eddy–mean flow interactions along the western boundary currents in the North Pacific [J]. Journal of Physical Oceanography, 49(3): 789-810.
YANG Y, LIANG X S, QIU B,, 2017. On the decadal variability of the eddy kinetic energy in the Kuroshio Extension [J]. Journal of Physical Oceanography, 47(5): 1169-1187.
YANG Y, LIU C T, 2003. Uncertainty reduction of estimated geostrophic volume transports with altimeter observations east of Taiwan [J]. Journal of Oceanography, 59(2): 251-257.
YANG Y, LIU C T, HU J H,, 1999. Taiwan current (Kuroshio) and impinging eddies [J]. Journal of Oceanography, 55(5): 609-617.
ZHANG D X, LEE T N, JOHNS W E,, 2001. The Kuroshio east of Taiwan: modes of variability and relationship to interior ocean mesoscale eddies [J]. Journal of Physical Oceanography, 31(4): 1054-1074.
DISTINCTLY DIFFERENT SEASONAL EDDY KINETIC ENERGY VARIATIONS AND THEIR MECHANISMS IN THE UPSTREAM AND DOWNSTREAM KUROSHIO WITHIN THE EAST CHINA SEA SECTOR
WANG Si-Wen1, YANG Yang1, LIANG Xiang-San2, 3, ZHAO Yu-Hui1, WANG Chang-You1
(1.School of Marine Sciences, Nanjing University of Information Science & Technology, Nanjing 210044, China; 2. Department of Atmospheric and Oceanic Sciences, and Institute of Atmospheric Sciences, Fudan University, Shanghai 200438, China; 3. Shanghai Qi Zhi Institute, Shanghai 200232, China)
Application of a new functional analysis tool, i.e., multiscale window transform (MWT), reveals to us distinctly different seasonal variation patterns of the eddy kinetic energy (EKE) in the upstream and downstream of the Kuroshio in the East China Sea. Based on a power spectrum analysis, the fields are orthogonally reconstructed with MWT onto two scale windows, namely, the background flow window (> 64 d) and the eddy window (< 64 d). The kinetic energy on each window is obtained accordingly with the MWT transform coefficients. In the upstream, the EKE peaks in August, and reaches its minimum in winter; in contrast, the EKE downstream has two peaks, one in April and another in September, and attains its minimum in winter. Using the MWT-based canonical transfer theory and localized multiscale energetics analysis, we find that barotropic instability and baroclinic instability are the main mechanisms for the EKE variations in this region. They govern the different EKE seasonal cycles in upstream and downstream Kuroshio, respectively. In the upstream, the EKE seasonality is mainly generated through a barotropic instability pathway (i.e. the canonical transfer of kinetic energy from the background flow to the eddies). In contrast, in the downstream, the April peak is determined by a baroclinic instability (i.e. the canonical transfer of available potential energy from the background flow to the eddies, which is further converted to EKE), while the September peak is jointly generated by a baroclinic instability and a barotropic instability.
Kuroshio; East China Sea; multiscale window transform; canonical transfer; barotropic instability; baroclinic instability
*国家自然科学基金项目, 41975064号, 41806023号; 2015江苏双创团队项目; 江苏省特聘教授项目。王思雯, 硕士研究生, E-mail: wswing1997@icloud.com
梁湘三, 教授, E-mail: xsliang@fudan.edu.cn
2021-10-08,
2021-11-23
P738
10.11693/hyhz20211000236
