基于理论与LS-DYNA耗能减震棚洞结构研究

2022-03-25夏永旭董子文

北京交通大学学报 2022年1期

梅华，王星，夏永旭，董子文

(1.湖南工学院 a.建筑工程与艺术设计学院，b.安全与环境工程学院，湖南衡阳 421002；2. 空军工程大学航空工程学院，西安 710038；3.长安大学公路学院，西安 710064)

落石是我国三大地质灾害之一，棚洞属常规被动防护结构，已有研究表明[1]：现有明洞一旦遭遇落石冲击，便导致结构损坏、失效.棚洞结构冲切破坏机理、新型落石防护措施已越来越成为相关学者研究的热点课题.

文献[2-5]采用理论计算、数值模拟、实例验证方法探究了落石对棚洞防护结构的冲切破坏机理，提出并验证了EPE+橡胶支座的改良效果.文献[6]以废旧轮胎作为棚洞防护结构垫层，并采用室内试验方法对其优越性进行了验证.文献[7-8]采用数值模拟方法研究了柔性防护结构在落石冲击作用下的力学响应机理.文献[9]采用试验与数值模拟方法分析了土体-EPS复合垫层在落石冲击作用下的力学响应特性.文献[10]基于试验与数值模拟方法探究了在不同冲击参数下棚洞结构的力学响应机理.文献[11]采用试验方法揭示了钢棚洞结构在复合垫层工况下的力学响应特性.文献[12]将柔性活塞杆应用于棚洞防护结构中，并通过室内试验对其优越性进行了验证.文献[13]采用试验与数值模拟方法研究了在落石冲击作用下，柔性棚洞结构的力学响应机理.文献[14]基于数值模拟方法探究了砂土-EPS复合垫层的力学响应特性.文献[15]采用数值模拟方法分别揭示了全拱式、半拱式、门式、直柱式、斜柱式棚洞的力学响应情况.文献[16]采用试验方法研究了落石对三开间单跨柔性防护结构的冲击效果.文献[17]结合数值模拟方法阐释了在不同落石冲击工况下棚洞防护结构的耗能缓冲机理.文献[18]基于数值模拟方法揭示了在落石冲击作用下柔性防护系统的能量衰减规律.

综上，目前关于落石冲击棚洞防护结构研究成果多聚焦于：①基于数值模拟方法分析落石对棚洞结构的冲切破坏机理；②砂土-EPS复合垫层的缓冲机理与效果；③钢丝网等柔性棚洞的防护机理与效果.鲜有学者采用理论方法揭示落石对棚洞结构的冲切破坏机理、推导顶板最大冲击应力算法，关于新型耗能减震复合垫层结构亦鲜有报道.

为此，本文作者拟基于落石冲切破坏棚洞结构过程，推导出在落石冲击作用下顶板腹部单元最大冲击应力；建立落石冲击棚洞结构的三维计算模型，对比验证数值模拟、理论计算结果，希冀为耗能减震棚洞结构研究提供借鉴与参考.

1 棚洞顶板冲击应力理论分析

1.1 棚洞顶板极限承载力计算

边坡危岩体崩落后，首先冲击棚洞结构上部垫层土体，垫层对冲击应力的扩散作用见图1.落石冲击侵彻完成后，存在关系式

(1)

式中：R为球体半径，m；R1为垫层土体上表面与落石球体相切圆面的半径，m；L为冲击侵彻深度，m.

图1 棚洞垫层的应力扩散作用Fig.1 Stress diffusion effect of shed-tunnel cushion

R2、R1之间存在几何关系

R2=R1+htanθ

(2)

式中：R2为冲击应力透过垫层在棚洞顶板上部的扩散半径，m；h为垫层厚度，m.

应力扩散角度θ(°)与垫层土体内摩擦角φ(°)之间的相互关系为

(3)

图2 落石冲切破坏棚洞顶板Fig.2 Roof of shed tunnel damaged by rockfall and punching

如果经缓冲垫层进行应力扩散后落石冲击应力仍然较大，棚洞顶板将会形成贯穿块体，图2为棚洞顶板贯穿块体结构示意图.

结合数值模拟及部分混凝土板冲击实验结果，采用弗拉索夫厚板原理计算时，遵循保守计算原则，贯穿块体下表面直径近似取上表面直径1.5倍.若棚洞顶板为薄板时，贯穿块体上下表面圆直径取近似相同，则有贯穿块体下部圆半径RP为

RP=3R2/2

(4)

混凝土板抗冲切破坏承载力Fu算法为

(5)

式中：d为冲击应力与混凝土板的接触直径，m；Hb为混凝土板厚度，m；fc为混凝土单轴有效抗压强度，Pa.

落石冲击应力与棚洞顶板接触直径d之间的关系表达式为

(6)

联立式(5)～(6)，则有

(7)

1.2 棚洞顶板平均冲击应力计算

基于落石最大冲击力与侵彻深度求取落石对棚洞顶板最大冲击应力.根据文献[19]室内试验研究结果，则有

(8)

(9)

(10)

式中：P为落石冲击力，N；M为落石质量，t；g为重力加速度，取9.8 m/s2；H为下落高度，m；t为冲击时间，s；Q为落石重量，kN；η为修正系数.

综上可得棚洞顶板腹部平均冲击应力Fp为

(11)

1.3 棚洞顶板最大冲击应力计算

由于棚洞顶板厚度较大，且顶板面积远大于落石横截面面积，忽略落石对板边的影响.根据弗拉索夫厚板原理[20]，以落石冲击作用点为中心选取棚洞顶板矩形计算区域，计算模型如图3所示，基于转角和挠度变量表达弗拉索夫板的平衡方程为

图3 棚洞顶板计算模型Fig.3 Roof calculation model of shed tunnel

(12)

(13)

(14)

式中：顶板区域长为2A，m；宽为2B，m；挠度为f，m；泊松比为υ；剪切变形模量为G，Pa；弹性模量为E，Pa；ωx为x=const截面的转角，rad；ωy为y=const截面的转角，rad；D为平板抗弯曲刚度，(N/m);q(x,y)为位于顶板(x,y)位置处作用力，N.

顶板内部的弯矩Mx、My计算表达式为

(15)

上述计算模型存在边界条件为

(16)

采用三角级数表示挠度f、转角ωx、ωy及荷载q，则有

(17)

式中：Xmn、Ymn、Zmn、qmn为三角级数系数；m、n为自然数.

联立式(12)、(17)，可得

(18)

令式(18)中自然数变量i=j=1，并将其代入弯矩表达式(15)，则有

(19)

考虑到x=A/2或y=B/2处存在最大弯矩Mmax，(N·m)，则顶板下部最大应力σmax计算式为

(20)

联立式(11)、式(20)，便可求得落石对棚洞顶板的最大冲击应力值.

2 落石冲击棚洞结构的数值模拟

2.1 建立数值计算模型

采用LS-DYNA软件建立落石冲击棚洞结构计算模型.落石球体选择刚性计算模型RIGID(020号材料)，棚洞顶板混凝土材料取HOLMQUIST_JOHNSON_CONCRETE材料模型，本构模型参数见表1[21].表1中，Aa为标准化内聚强度；Bb为标准化硬化压力；N为压力硬化指数；Smax为标准化最大强度；Plock为锁定压力；K1、K2、K3为压力常数；D1、D2为损伤常数；C为应变率系数；EFMIN为断裂前塑性应变量.土垫层采用DRUCKER-PRAGER计算模型(193号材料).所有材料单元均取SOLID164.

表1 普通混凝土HJC本构模型参数

D-P屈服准则屈服面在主应力空间内为一圆锥面，如图4(a)所示，在π平面内为圆形，如图4(b)所示，图4中1、2、3表示主应力代号.

图4 D-P准则屈服面Fig.4 Yield surface of D-P criterion

D-P屈服准则的屈服函数表达式为

(21)

I1=σ1+σ2+σ3

(22)

(23)

式中：I1为应力状态第1不变量；J2为应力偏张量第2不变量；σ1、σ2、σ3分别为第1、2、3主应力，Pa.σx、σy、σz为x、y、z方向应力，Pa；τxy、τyz、τzx分别为xy、yz、zx平面切向应力，Pa.

系数α、k与黏聚力c(Pa)、内摩擦角φ(°)之间的关系分别为

(24)

(25)

计算模型中长、宽均取5.0 m，棚洞顶板采用C30混凝土，厚度取0.5 m，土垫层厚度为0.5 m，落石直径为1.0 m.对顶板四周节点实施全约束.落石法向冲击速度分别取为6、10、14、18 m/s，计算时间取0.06 s，计算步取100步.在落石冲击中心区域进行适当加密.数值模拟计算参数如表2，数值计算模型见图5.

表2 数值模拟计算参数

图5 砂土-顶板模拟计算模型Fig.5 Sand-roof simulation model

2.2 计算结果分析

图6为在不同落石冲击时刻下，棚洞顶板结构的等效应力分布云图.由图可知，顶板中心位置始终处于应力集中状态，板内部应力呈波动状态.落石冲击作用对棚洞顶板结构的损伤呈现瞬态脉冲性、就近损伤原则.

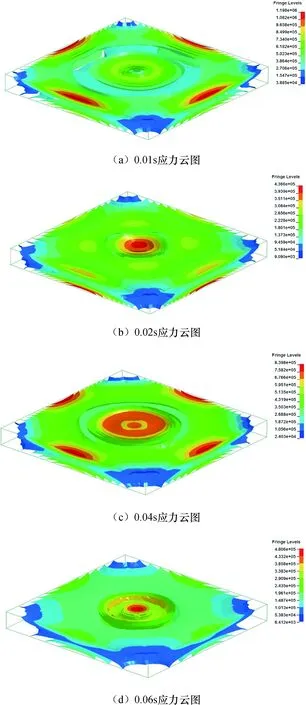
图6 砂土垫层顶板应力变化云图Fig.6 Cloud diagram of stress variation in sand cushion roof

图7为在不同落石冲击速度情况下，棚洞顶板结构腹部中心单元的应力变化曲线.冲击应力曲线整体呈现出明显的脉冲式波动状态，在0.06 s冲击时间内共形成了4次波动，且随冲击时间推移波峰值会逐步下降.各计算工况下顶板单元冲击应力约在0.014 s达到峰值状态.当落石冲击速度为14、18 m/s时，顶板单元冲击应力可达2.39、3.17 MPa，超过C30混凝土极限抗拉强度2.2 MPa，造成顶板结构受拉破坏.

图7 顶板腹部正中单元应力变化曲线Fig.7 Stress variation curve of midline unit in roof middle

2.3 理论计算与数值模拟验证

图8 顶板平均冲击应力Fig.8 Average impact stress of roof

图8为在落石冲击应力作用下，由式(11)计算得出的顶板平均冲击应力计算结果.各计算工况下顶板腹部平均应力值均相对偏小，当冲击速度为18 m/s时，平均冲击应力为1.759 MPa，棚洞结构此时仍处于安全状态，这与数值计算结果偏差较大，可见若以平均冲击应力作为顶板结构冲切破坏与否的考核指标将存在一定偏差.究其原因，在落石冲击棚洞顶板过程中，冲击应力并非按照均匀状态散布于顶板腹部圆形区域，落石冲击应力会在短时间内上升至峰值且会在顶板腹部正中单元处形成应力集中状态，继而以脉冲形式向外波动扩散.

联立式(11)、式(20)求取棚洞顶板腹部正中单元最大冲击应力，并将其与数值模拟计算结果相对比如图9所示.各计算工况下理论计算结果与数值模拟结果相互吻合，验证了理论、数值模拟算法的可靠性.冲击速度在6 m/s～18 m/s时，两种算法结果偏差分别为10.41%、7.18%、7.95%、1.09%，其中数值模拟计算结果略有偏小，这或是由于在落石冲击力计算中尚未考虑落石与垫层土体之间的摩擦生热耗能因素.

图9 理论-数值模拟计算结果Fig.9 Theoretical-numerical simulation results

2.4 棚洞顶板冲击破坏分析

以棚洞顶板极限受拉应力作为结构破坏与否的评判标准.图10为混凝土受拉应力标准、理论计算应力、数值模拟应力的统计结果.由图可见，理论计算、数值模拟结果均显示：在落石冲击速度约达到12 m/s时，棚洞顶板混凝土即会被冲切破坏.

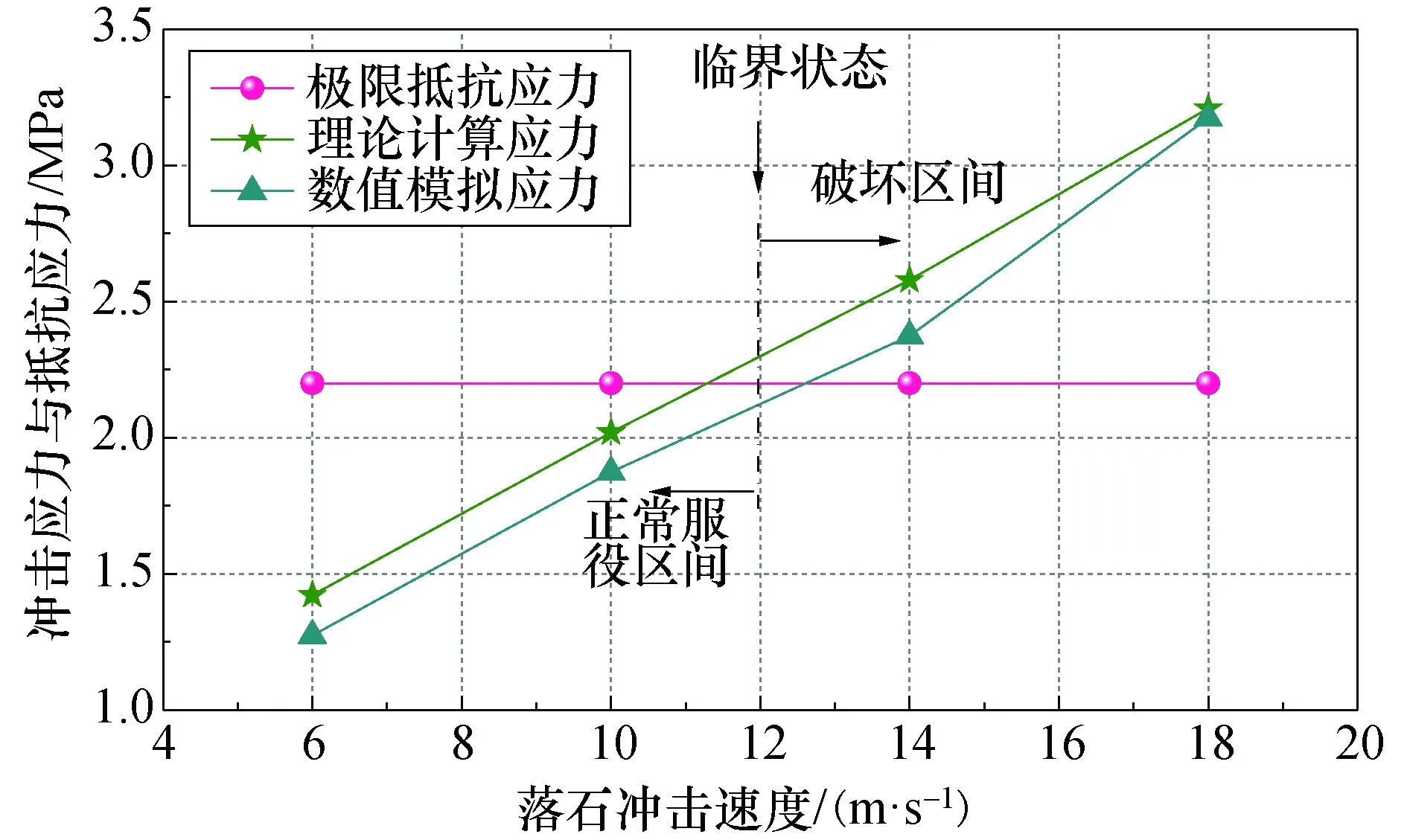
图10 落石冲击应力-顶板抵抗应力Fig.10 Rockfall impact stress-roof resistance stress

图11为采用式(7)所得顶板抵抗力与采用式(8)所得落石最大冲击力之间的统计结果.随着落石冲击速度增加，冲击应力的扩散范围将会有所增加，致使顶板冲击力抵抗值亦略有升高.图11显示在落石冲击速度达到约12 m/s时，即落石冲击力达到0.7 MN时，顶板结构将无法抵御冲击力而形成冲切破坏，与图10所得结论保持一致.