基于桥面不平顺的车辆舒适性分析

李武生，王贵春

(1. 机械工业第六设计研究院有限公司，郑州 450007；2. 郑州大学 土木工程学院，郑州 450001)

当车辆在大跨度桥梁上高速行驶时，由于桥面不平顺的激励效应，车辆与桥梁均会产生随机振动，而车桥间的动力相互作用又会使振动加强[1].上述现象严重影响司乘人员的乘坐质量.通常把运行车辆为司乘人员提供舒适程度的性能称为车辆舒适性，它既与道路状况有关，也与车辆本身的性能及运行参数有关.研究车辆舒适性问题先是分析车桥耦合振动计算车辆的动力响应，然后通过某种方法建立车辆舒适性与车辆动力响应的关系，进而对车辆的舒适性做出评价.

车辆在运行过程中，表现出的跳动、横摆、摇摆、侧倾及俯仰等振动现象，是影响车辆舒适性的直接原因.对车辆振动响应的研究也已取得较大成绩.文献[2]采用桥面实测数据和三维桥-车模型，计算出载重车辆的动态车轮荷载和加速度响应, 并将计算值与实测数据进行对比分析，获得较好效果.文献[3]建立货车-路面-组合钢梁桥综合数值分析模型，将振动计算值与实桥行车动力试验结果进行对比，以验证计算方法的可靠性，分析了车型、钢梁高宽比、桥墩顶部混凝土桥面板接缝及弹性垫刚度对车桥相互作用及由此产生可感知振动的影响.

车辆动力响应严重到一定程度，会直接降低司乘人员的舒适感.目前，对车辆舒适性的研究也已取得了长足进步.文献[4]通过现场测试，得到了5座桥梁及相应运行车辆的动力响应数据，采用小波变换方法研究行车内部振动规律，并对行车舒适性进行评价.文献[5]将风荷载考虑到大跨度斜拉桥的车桥耦合振动系统中，采用数值分析法模拟路面不平顺，研究横向风荷载及车速变化对行车舒适性的影响.文献[6]将人、车、桥构建为空间耦合系统，分析三者的振动响应，更准确地对乘坐舒适性进行评价.文献[7-8]为了研究行车舒适性，将风、车、桥看作一个空间时变耦合振动系统，计算振动响应，提出了行车安全性与舒适性评价方法.文献[9]建立了风-车流-桥耦合振动系统模型，并考虑车流随机性、邻近汽车干扰、桥面恶化等因素影响，评价车辆的舒适性.文献[10]将车辆简化为移动荷载，施加于桥梁节点上，研究了悬索桥的动力响应和行车舒适性问题.

上述研究侧重于分析单辆车过桥的情况，且在评价行车舒适性时考虑的振动形式相对单一.影响行车舒适性的因素繁多，加之车桥耦合振动系统的复杂性，有必要对核心问题进行更精细的研究[11].为了深入探索车队过桥时的行车舒适性问题，本文作者以福建长门大桥为背景，建立多自由度车辆模型，研究不同桥面不平顺等级下的行车振动响应，依据ISO2361-1—1997方法[12]分析车辆舒适性与其振动加速度的关系.

1 桥梁、车辆分析模型

1.1大跨度斜拉桥三维有限元模型

福建长门大桥中跨为钢箱梁，跨长550 m.边跨为钢筋混凝土梁，索塔为花瓶型，有限元模型见图1.

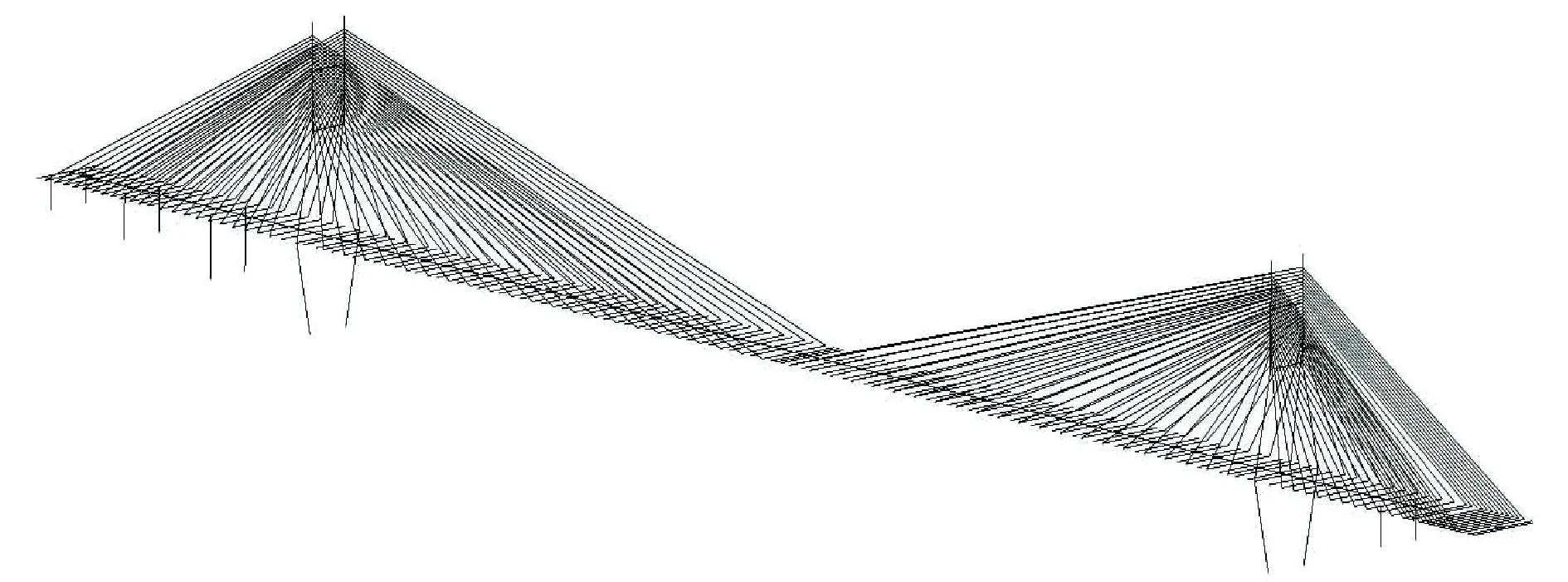
图1 桥梁有限元模型Fig.1 Bridge finite element model

图2为车辆在桥面上的布置图.

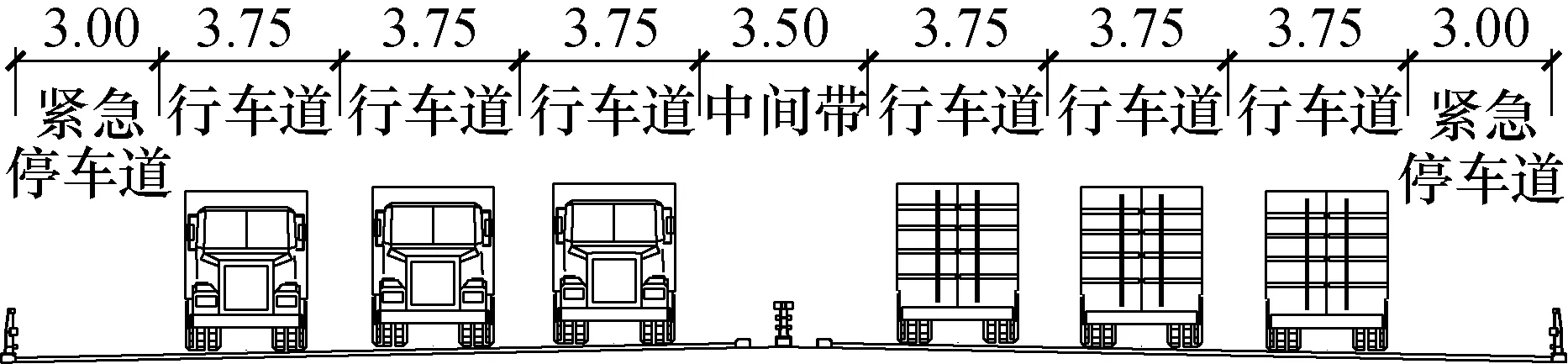
图2 车道布置示意图(单位：m)Fig.2 Schematic diagram of vehicle lane layout(unit: m)

在Ansys平台上，主梁采用考虑扭转、剪切变形的beam188单元、索塔采用beam4单元，以受拉杆link10单元模拟拉索.本文利用Ansys非线性分析功能，将拉索等效弹性模量定义为

(1)

则斜拉索应力应变关系为

(2)

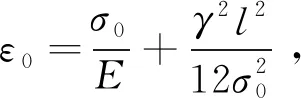
1.2 车辆空间模型

图3为9个自由度的车辆模型，其中m1～m6、z1～z6分别为6个车轮的质量和竖向位移；mv、zv分别为车体质量和竖向位移；θv、φv分别为车体俯仰、侧倾方向的角位移；ku1～ku6、kd1～kd6分别为车悬架刚度和轮胎刚度；cu1～cu6、cd1～cd6分别为车悬架阻尼和轮胎阻尼.

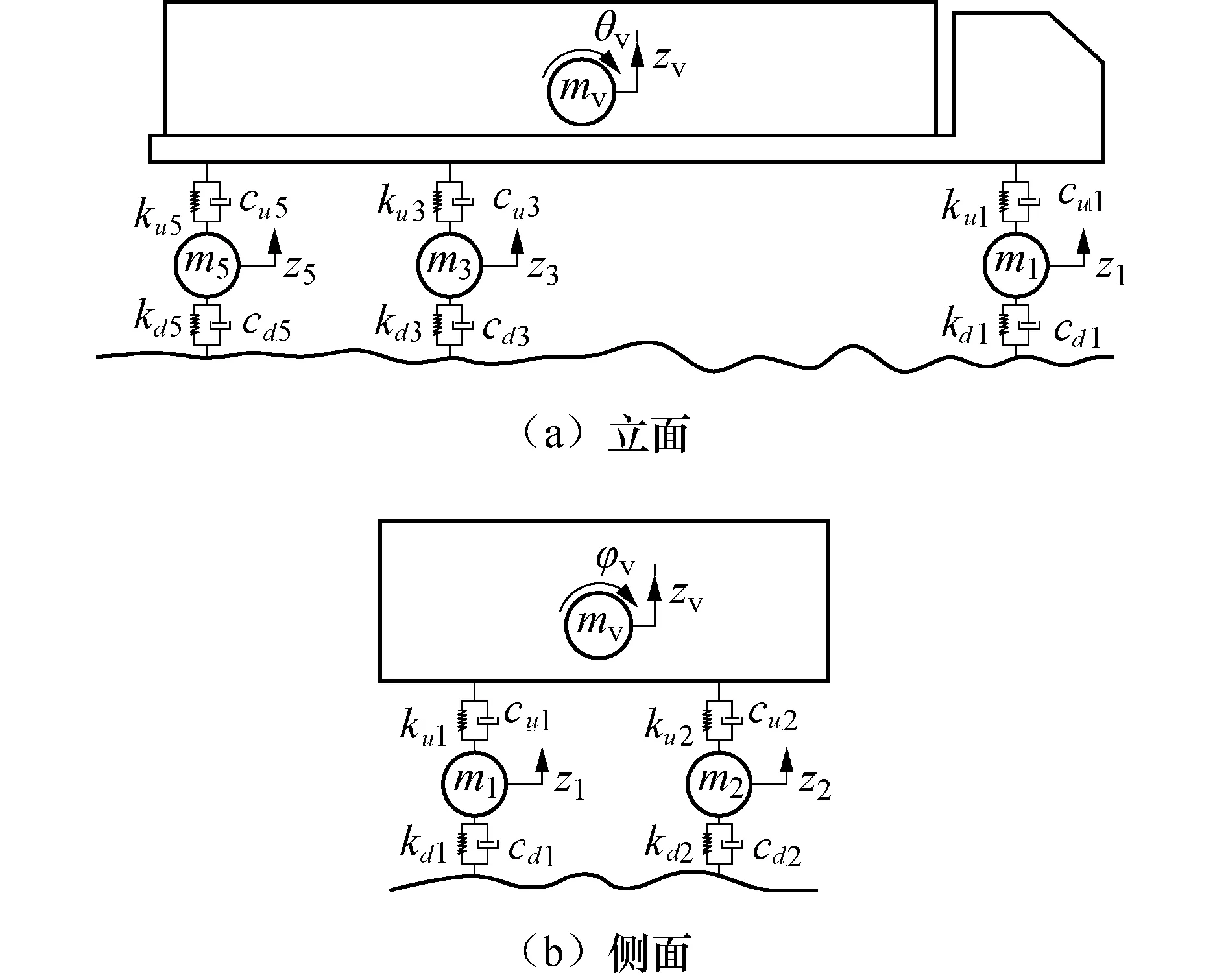
图3 车辆模型Fig.3 Vehicle model

1.3 路面不平顺模拟

根据我国国家标准中关于路面不平顺的表示方法[13]，用功率谱密度拟合路面不平顺的统计特性.其功率谱密度Gd(nk)为

Gd(nk)=Gd(n0)(n/n0)-w

(3)

式中：nk、n0分别为空间频率和参考空间频率，n0=0.1m-1；Gd(n0)为路面不平度系数；w为频率指数.本文采用数值分析方法对路面不平顺进行模拟，而通常认为桥面不平顺与一般道路的路面不平顺是一致的.参考利用三角级数法模拟桥面不平顺，以桥梁起点为原点，可将桥面上距原点为x值的任意点的不平顺值表示为

(4)

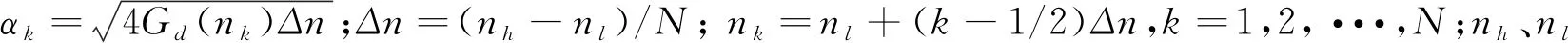
国家标准[13]按功率谱密度将路面分为八级，本文选取较为常见的A、B、C、D四个等级.以B级路面为例，计算得到不平顺样本如图4所示.

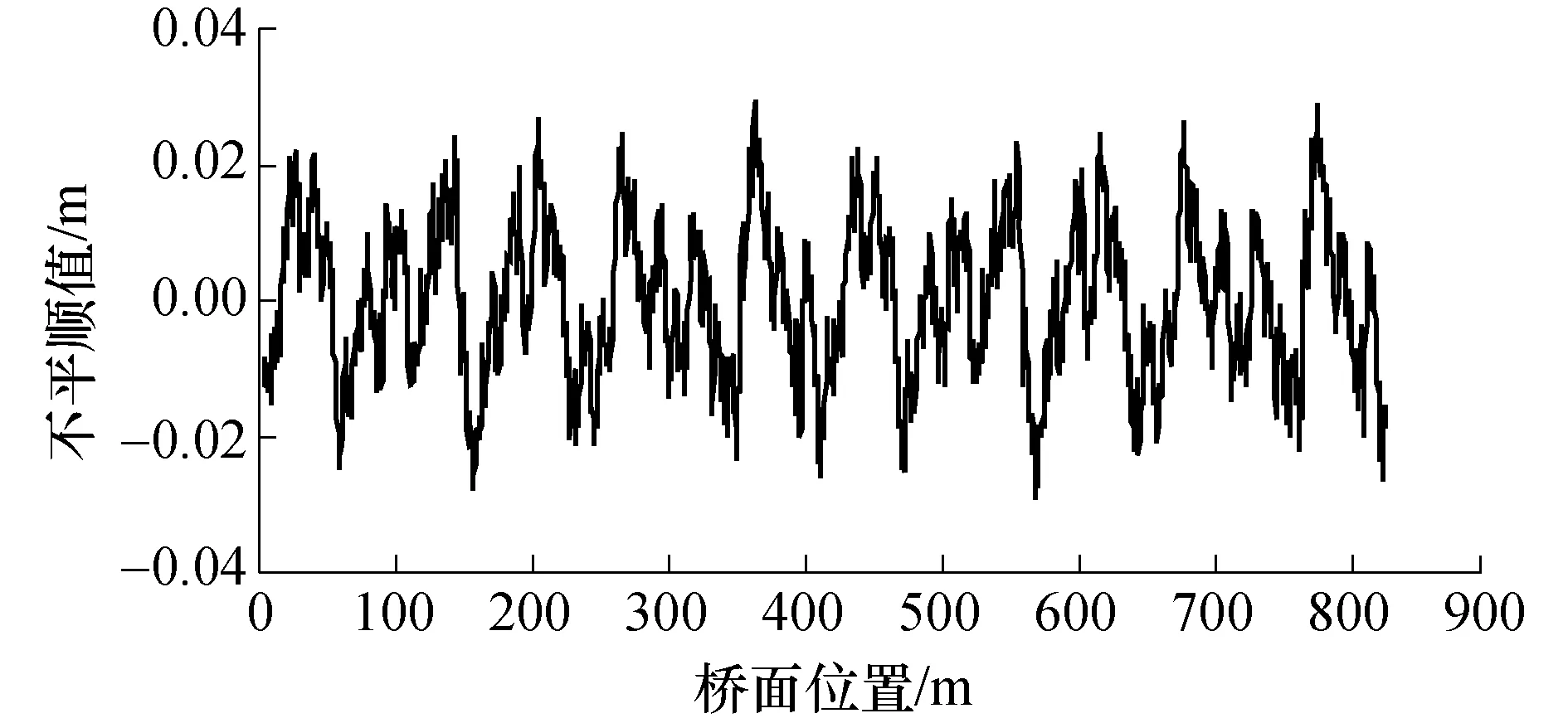
图4 B级路面不平顺样本Fig.4 Sample of grade-B road irregularities

图5为不平顺峰值变化曲线，可以看出，不平顺峰值从A级到D级依次增大，表明路面越来越粗糙.

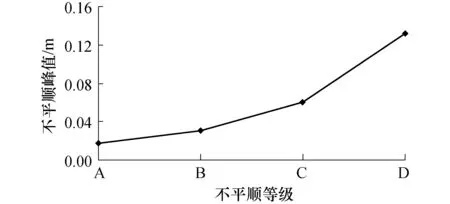
图5 路面不平顺峰值变化曲线Fig. 5 Variation curve for peak values of road irregularities

2 振动微分方程及收敛准则

2.1 振动微分方程

车与桥通过轮胎接触点传递动力并互相影响，根据两者作用关系，作如下假定：

1)车轮与桥梁不脱离，两者竖向相对位移向量ΔZ(t)为

ΔZ(t)=Zb(t)-Zv(t)+r(x)

(5)

式中:Zb(t)、Zv(t)分别为桥、车轮在二者接触点处的竖向位移向量；r(x)为桥面不平顺值向量.

2)车、桥之间作用力为一组反向等值力，即

(6)

式中:Pb(t)、Pv(t)为车辆与桥梁的相互作用力向量；Cd、Kd分别为轮组的阻尼和刚度矩阵.

根据以上车、桥关系假定，分别建立车和桥的振动微分方程，其矩阵形式为

(7)

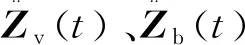
2.2 振动微分方程的求解及收敛准则

采用Newmark-b法进行振动微分方程的迭代求解.在求解过程中利用式(5)和式(6)的位移和作用力关系，将式(7)耦合起来 .该方法有两个假定：

(8)

2) 在t+Δt时刻，Zt+Δt计算式为

(9)

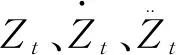
下面以式(7)为例说明求解要点，为表述方便，省略式中矩阵下角标.

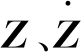
2) 设定积分参数β、γ及时间步长Δt，计算积分常数

α6=Δt(1-β)，α7=βΔt

3) 计算等效刚度矩阵

(10)

4) 逐步进行时间步计算.

①计算t+Δt时的等效荷载向量

(11)

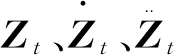
②求解t+Δt时刻的位移

(12)

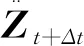
(13)

(14)

以位移容差为收敛条件，即

(15)

式中：‖Zt+Δt‖表示Zt+Δt的范数；ε为位移收敛控制参数；ε取值大小将关系到后续计算量与结果精度，本文取ε=0.01.

3 行车舒适性分析方法

司乘人员受到行车传来的振动，主观感觉会随着振动大小而变化.人体对剧烈振动的忍耐能力较差，会快速出现不适感，进入疲惫状态，而对微小振动的承受能力较强，可以长时间保持精神稳定状态.将人体在行车中的舒适感以定量的方式准确表达，是研究行车舒适性的目的，一般以人体多部位的振动加速度作为衡量参数.国际标准ISO2631[12]的总加权值法根据人体不同部位对振动不适感的权重大小，对多个自由度的振动加速度进行加权统计，能够考虑到人的主观感受与振动的实际情况，是一种较为合理的评价方法.

本文采用ISO2631的总加权值法，将坐姿人体承受振动的部位简化为三处，即脚部、臀部、后背，车辆振动通过此三个接触部位作用于人身.

图6为车内坐姿人体承受振动的方向坐标示意图，共12个自由度.

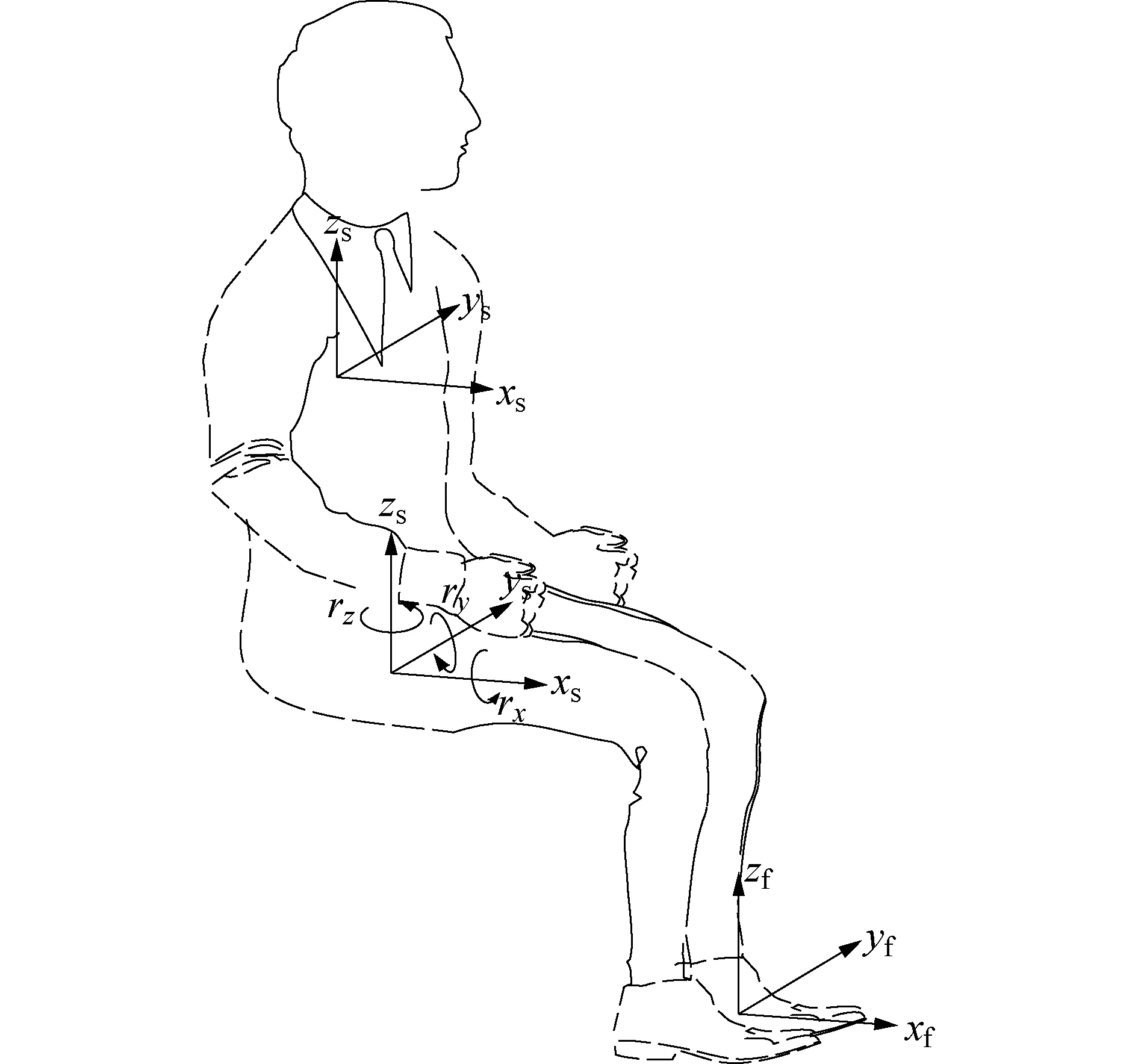
图6 人体坐姿的坐标系Fig.6 Coordinate system of human sitting posture

1) 座面与臀部接触面中心有6个自由度，三个振动线位移xs、ys、zs和三个振动角位移rx、ry、rz；

2) 靠背合力作用点处有3个自由度，即背部振动线位移xb、yb、zb；

3) 脚与车地板接触面处有3个自由度，即双脚振动线位移xf、yf、zf.

将以上12个方向的振动综合考虑，加权计算得到均方根值av，作为舒适性评价参数

(16)

式中：N为自由度数；aωi、ki分别为第i个加速度均方根值和权重系数.

行车通过坐椅传递给人体的振动主要有竖向、侧倾和俯仰三个方向，由此将av写成

(17)

式中：aω1、aω2和aω3分别为竖向、俯仰、侧倾三个方向的振动加速度均方根值；加权系数k1=1、k2=0.4 m·rad-1、k3=0.63 m·rad-1.

加权振级计算公式为

Leq=20lg(av/a0)

(18)

式中：a0为参考加速度均方根值，a0=10-6m·s-2.

将计算结果对照表1，可进行评价人体主观舒适感觉.

表1 乘坐舒适性评价表

车辆驶过桥梁引起的车桥系统振动是一个复杂的随机过程.随着行车位置的改变，桥面不平顺值、车辆和桥梁的振动状态均在发生变化，因而每个时间步的初始条件各不一样.本文在Ansys平台上求解车辆动力响应，进而研究行车舒适性.

4 计算实例

在下面计算实例中，车辆间距采用随机小幅变化，值为50 m～55 m之间，设车速为20 m·s-1.车辆参数取值如下：

m1=m2=335 kg；

mv=24 990 kg；

m3～m6均为670 kg；

kd1=kd2=2 680 kN•m-1；

ku1=ku2=718 kN•m-1；

kd3～kd6均为4 809 kN•m-1；

ku3～ku6均为1 652 kN•m-1；

cd1～cd6均为2 340 kg•s-1；

cu1～cu6均为2.4×105kg•s-1；

4.1 车体振动加速度分析

图7给出了三个方向的加速度对比图，与A级不平顺的情况相比，在D级不平顺时三个方向加速度幅值均明显增大，这表明在D级不平顺时行车振动更剧烈.

图8为车体的振动加速度峰值随桥面不平顺等级变化的曲线图.

由图8可知，对于A级桥面，三个方向的振动加速度峰值最小，分别为1.32 m•s-2、1.26 rad•s-2、3.60 rad•s-2，B、C、D级桥面时峰值依次增大.当桥面不平顺为D级时，三者最大，分别为9.80 m•s-2、9.71 rad•s-2、23.13 rad•s-2，分别增大7.42、7.71、6.43倍.因此，行车振动受桥面状况影响比较明显，路况恶化会加剧行车振动.

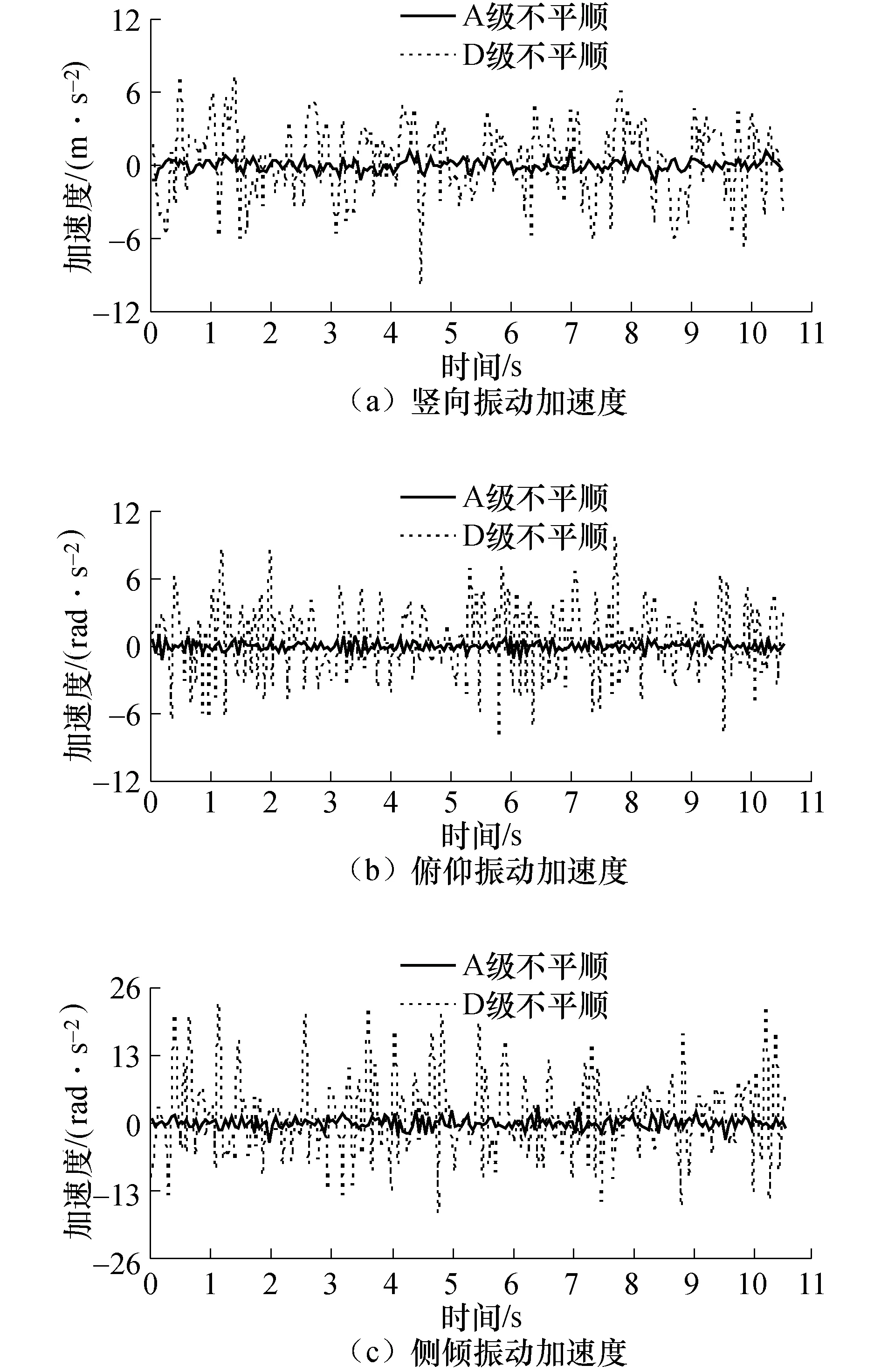
图7 加速度时程曲线对比图Fig.7 Comparison of acceleration time-history curves

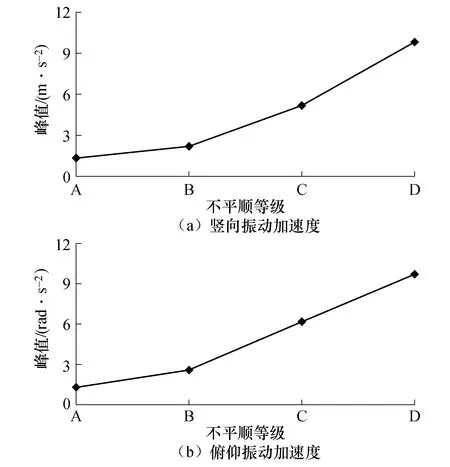
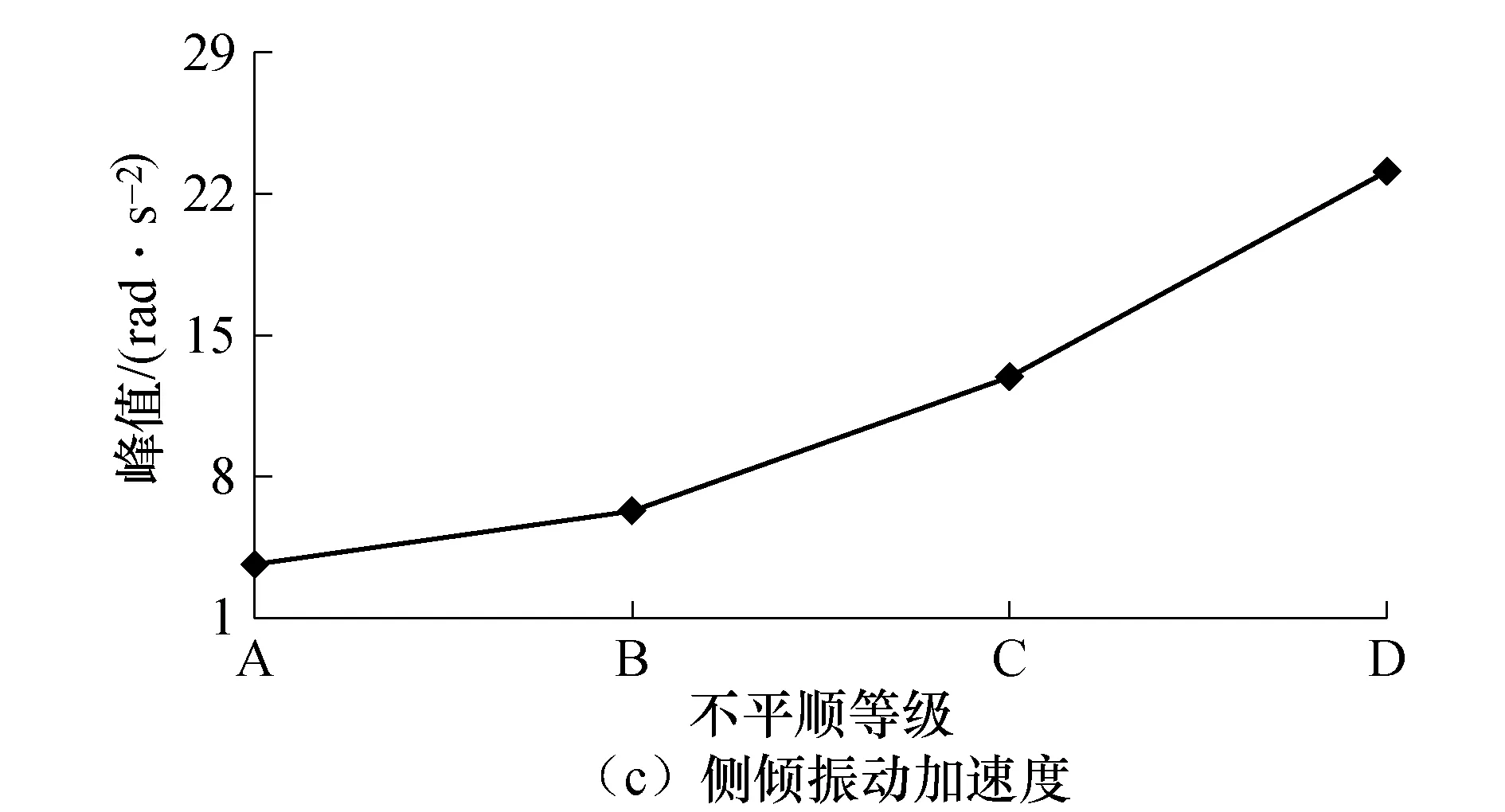
图8 振动加速度峰值与桥面不平顺的关系曲线Fig.8 Relationship curve between peak values of vibration accelerations and bridge deck pavement irregularity

4.2 车辆舒适性分析

图9所示为加权振动加速度均方根值与桥面不平顺等级的关系曲线.表2所列为根据总加权振动加速度均方根值所进行的行车舒适性评价.

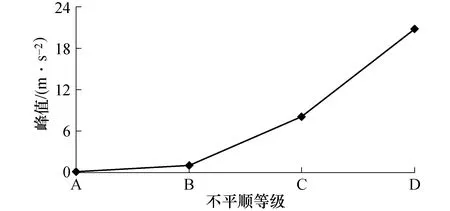
图9 加权振动加速度均方根值与桥面不平顺的关系曲线Fig.9 Relationship curve between bridge deck pavement irregularity and weighted vibration acceleration root mean square value

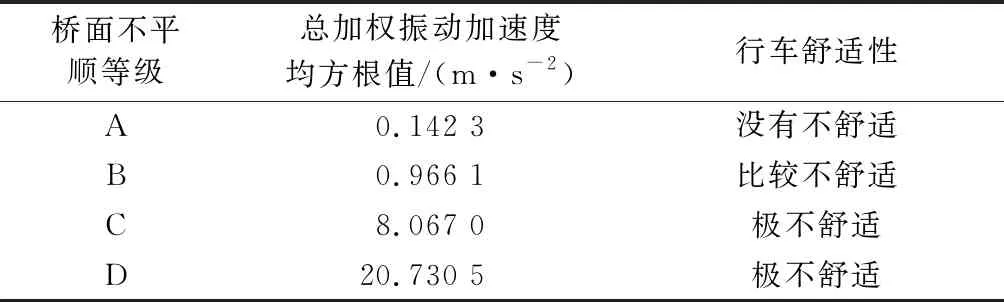
表2 行车舒适性分析

从图9可以看出，总加权加速度均方根值随桥面不平顺等级变化非常明显.在A级不平顺时此数值最小，为0.14 m•s-2<0.315 m•s-2，可将行车评定为没有不舒适.在B级不平顺时此数值有所增大，为0.97 m•s-2，在0.5～l m•s-2范围内，可将行车评定为比较不舒适.在C级、D级桥面时此值急剧增大，分别为8.07 m•s-2、20.73 m•s-2，均明显超出2 m•s-2限值，可将行车评定为极度不舒适.

5 结论

1) 当桥面不平顺由A级变到B级时，车辆振动加速度增大缓慢；当桥面不平顺由B级变到D级时，车辆振动加速度增大较快.与A级桥面的情况相比，D级桥面的竖向、俯仰和侧倾振动加速度分别增大了7.42、7.71、6.43倍.

2) 随着桥面路况变差，行车舒适性变化较大.就本文中的计算工况做出车辆舒适性评价为：对于A级桥面，没有不舒适;对于B级桥面，比较不舒适;对于C、D级桥面，极度不舒适.

3)本文只分析了桥面不平顺引起的车辆舒适性问题，在实际情况中，涉及的桥梁会更加复杂，如公铁两用桥、跨海大桥、老化桥梁等；分析工况也会更加多样，如地震、风、车辆超载、车辆撞击等因素的引入.考虑这些复杂情况，使车辆舒适性的研究更接近于真实环境，将是我们进一步的研究方向.