基于改进人工势场法的车辆局部路径规划研究

范思汉　张洪信

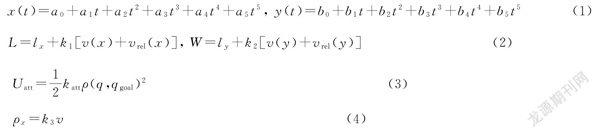
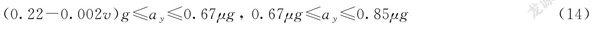
文章编号： 10069798（2022）01005008; DOI： 10.13306/j.10069798.2022.01.008

摘要：  针对人工势场法应用于结构化道路中的汽车主动避障领域存在规划能力，路径平滑度不足以及易陷入局部最优的问题。本文提出了一种结合人工势场法和五次多项式避障轨迹的路径规划算法，满足汽车避障时的安全性、实时性要求。通过引入五次多項式势场边界，结合汽车与障碍物的运动状态设计边界参数，提高路径平滑度和安全性。通过设置随动目标点优化引力模型，调节因子优化势场函数，可消除局部最小点。利用车辆动力学仿真软件Carsim/Simulink搭建仿真环境，并使用Stanley方法进行路径跟踪。仿真结果表明，所提出的算法可在动、静态环境中有效的规划出满足汽车行驶要求的避障路径。该算法为汽车避撞时的局部路径规划提供了参考依据。

关键词：  智能车辆; 主动避撞; 路径规划; 人工势场法

中图分类号： U461.91; TP391.9文献标识码： A

主动避障技术是无人驾驶汽车的关键技术之一[1]。汽车主动避障技术分为速度控制避障和转向控制避障。汽车转向控制避障的开发和应用还处于起步阶段[2]。避障局部路径规划是汽车转向避障的核心技术，对于发展无人驾驶技术具有重要意义。汽车主动避障局部路径规划算法主要有插值曲线法、人工势场法和智能规划方法等[35]。传统人工势场法由O. KHATIB提出[6]，广泛应用于移动机器人实时避障领域[7]。该方法具有计算简单、实时性好、对检测偏差具有一定的鲁棒性等优点，但存在陷入局部最小点和目标不可达等缺点[8]。基于此部分学者对势场模型和算法融合进行了改进。王树凤等人[9]建立新型障碍物虚拟力场模型，实现汽车超车路径规划;唐志荣等人[10]引入道路边界模型，运用二位正态分布势能函数，改善了路径平滑度;王其东等人[11]引入车辆速度参数，提出了一种参数时变人工势场模型，提高了车道保持行为的控制精度;刘翰培等人[12]在危险区域融合模糊控制算法，克服了传统人工势场法的局部最小值问题;ZHOU Z Y等人[13]结合粒子群算法优化切向向量，改善了路径不可达问题;豆祥忠[14]通过引入距离比函数来解决目标不可达问题，通过设置虚拟障碍物使车辆能够跳出局部最小点;SONG X L等人[15]结合弹性绳理论和人工势场法，实现了汽车在直道和弯道上的高速避障路径规划。但单一的改进势场模型难以改善传统人工势场法共线或多障碍物导致的局部最优和目标点不可达等多个缺陷，基于算法融合的方法则往往会使计算量增大，消除了传统人工势场法本身的高实时性优势。因此，本文考虑汽车行驶时的运动状态、安全性和合法性要求，提出了一种改进人工势场算法，该算法满足汽车避障时的安全性和实时性要求，仿真实验结果验证了算法规划汽车避障路径的有效性。该研究为无人驾驶技术提供了理论参考。

1势场模型

1.1势场边界模型

传统人工势场法大多将障碍物看作质点，规划出的路径难以满足汽车中高速行驶时的要求。将势场边

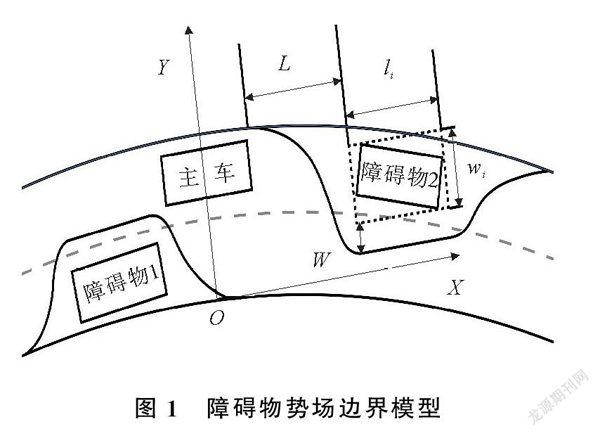
图1障碍物势场边界模型界化为圆形或椭圆形能够改善规划路径的平滑度，但避障轨迹仍与汽车实际行驶轨迹差别较大。由于五次多项式路径曲率连续，与驾驶员实际转向避撞行驶轨迹类似[16]，本文采用五次多项式作为障碍物虚拟势场边界，障碍物势场边界模型如图1所示。结构化道路由平面线形、直线、平曲线组成[17]，几何特征明显，是无人驾驶技术较容易得到应用的场景之一。

将受控车辆称为主车，以右侧车道边界线为原点，X轴与车道边界相切，Y轴与主车相交，建立随动笛卡尔直角坐标系。行车时可能遇到的障碍物几何结构各异，统一采用将障碍物完全包围的矩形作为障碍物边界，设障碍物长为li，宽为wi。已知障碍物坐标、角度、尺寸等信息，计算可得到矩形边界各点。设障碍物接近道路中心矩形边界角点横向距离W处的位置，障碍物矩形边界纵向距离L处的车道边界点两处为控制点。

设五次多项式边界表达式为

其中，x为边界纵向坐标;ai（i=1～5）为纵向拟合系数;t为避障时间;y为边界横向坐标;bi（i=1～5）为横向拟合系数。

在汽车实际行驶中，车辆行驶速度越大，避障距离越远，此外避障距离还受相对速度的影响。将主车速度和与障碍物相对速度引入五次多项式，控制点距离为

其中，lx为纵向预留安全距离;k1为纵向增益常数;v为主车行驶速度;vrel为与障碍物的相对速度;ly为横向预留安全距离;k2为横向增益常数。

将障碍物尺寸纳入斥力势场边界，对障碍物前方和后方采用五次多项式势场边界;对障碍物侧方，采用直线段作为势场边界。以图1中的主车与障碍物1为例，设障碍物1坐标（x1，y1），主车坐标（x，y），

在x>（x1+li/2）或x<（x1-li/2）处，采用式（1）计算虚拟边界，否则为y=y1-W 。

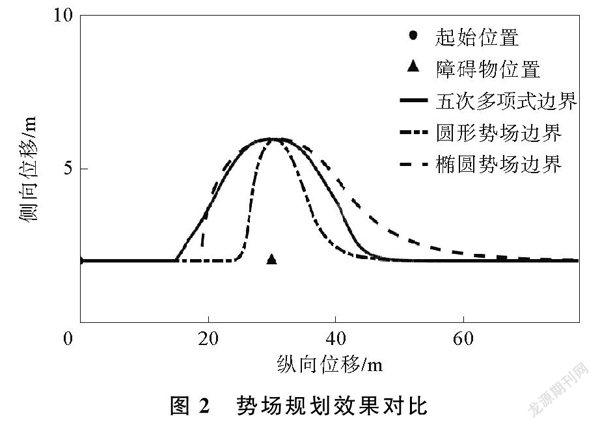
势场规划效果对比如图2所示。当主车、障碍物和目标点接近三点共线时，传统势场和椭圆形势场在避障开始时路径曲率较大，其曲率大小主要受与障碍物横向距离的影响，难以调整。采用五次多项式势场边界规划的路径，初始阶段曲率更小，其曲率变化主要受避障纵向距离的影响，易于控制。采用五次多项式势场边界规划出的路径，更符合汽车行驶要求。

1.2引力势场函数模型

传统人工势场法引力势场函数为

其中，Uatt为引力势能;katt为引力增益因子;ρ（q，qgoal）为主车与障碍物之间的欧氏距离。

为使汽车在避障完成后能够继续向前行驶，以主车前方ρx处的车道中心点代替固定目标点，汽车将受到引力的持续牵引。目标点距离与车速成正比，其计算方式为

其中，ρx为目标点距离;k3为目标点距离比例系数;v为主车车速。

传统人工势场法可通过katt调整引力场强度，由于受到各方向上引力强度比例相同，可能导致汽车返回车道中心路径过长，增加汽车变道时风险。将引力势能沿随动坐标系分解，引力势能分解后可以针对不同方向的引力进行单独调节。增大Y方向的牵引力能够使汽车更快返回车道，通过加入引力调节因数σ，增强Y

方向的引力势能变化。σ计算方式为

其中，s为引力调节常数，满足s≥道路宽度。

改進后的引力势场为

引力场的负梯度是主车所受引力，即

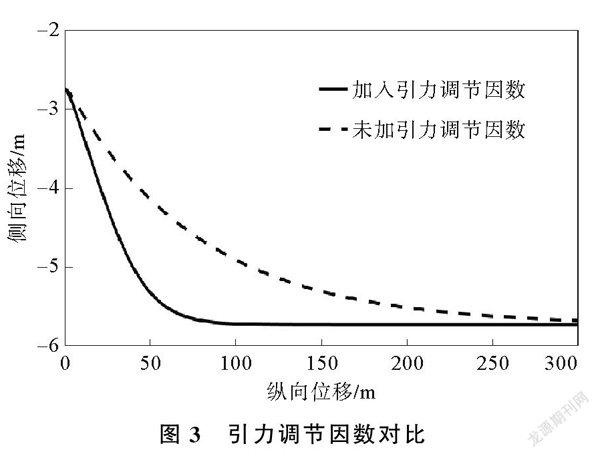
引力调节因数对比如图3所示，未加入引力调节因数时，汽车返回车道轨迹较为平缓。引入引力调节因数后，汽车返回原车道速度明显加快，返回路径明显缩短。在实际的车辆行驶中，及时变道具有重要安全意义，在行驶路径满足车辆行驶的条件下，变道时间越短，安全性越高。因此，改进后的引力势场模型安全性更高。

1.3道路边界势场模型

汽车在结构化道路上行驶时受到车道边界的约束，因此需要增加道路边界势场，将汽车的可行驶区域限制在道路之内。行驶的汽车不允许连续变道，因此汽车换道避障时仅考虑通过单次换道完成避障，故进一步将势场边界限制在汽车相邻车道内。对于多车道道路，使用汽车所在车道与内侧相邻车道为道路势场边界，若汽车已经处于最内车道，则与外侧车道组成道路势场边界，道路边界势场函数为

其中，Ur为道路边界斥力势能;kr为斥力增益因子;ρ（q， qr）为主车到道路边界的最短距离;ρ0为斥力影响范围。主车所受道路边界斥力为斥力场的梯度，道路边界斥力为

1.4障碍物势场模型

传统人工势场法中目标距离为主车与障碍物边界的最小距离，本文以主车与障碍物势场边界沿Y方向的距离代替。由于障碍物势场边界将障碍物边界完全包含在内，减轻了车辆行驶时误差的影响，保证了安全性，同时计算量更小，主车将只受到沿随动坐标系Y方向的斥力，与引力叠加后的合力方向将被限制在主车前方，消除了局部最小点。斥力势场函数为

其中，Ureq为障碍物斥力势能;ρy（q，qobs）为主车到障碍物势场边界沿Y方向的距离。

主车所受障碍物斥力为斥力场的梯度，障碍物势场斥力为

将式（6）、式（8）和式（10）相加，得总势场函数为

总势力函数为

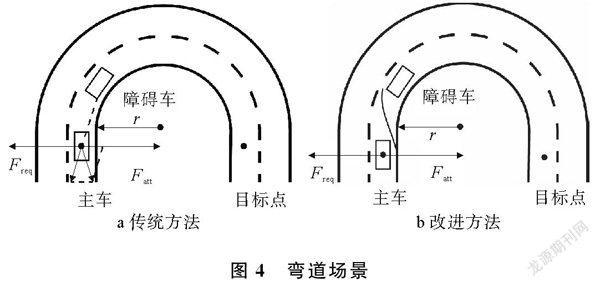
上述斥力势场模型与引力势场模型结合，在可通行区域内消除了局部最小点。以U形弯道为例，弯道场景如图4所示，传统人工势场法，当引力与斥力夹角过大时，出现引力斥力相抵消，导致汽车无法前进，陷入局部最小点。改进方法通过设置ρx小于等于道路圆曲线最小长度πr，汽车不会陷入局部最小点，规划路径不会出现停滞或倒退现象。

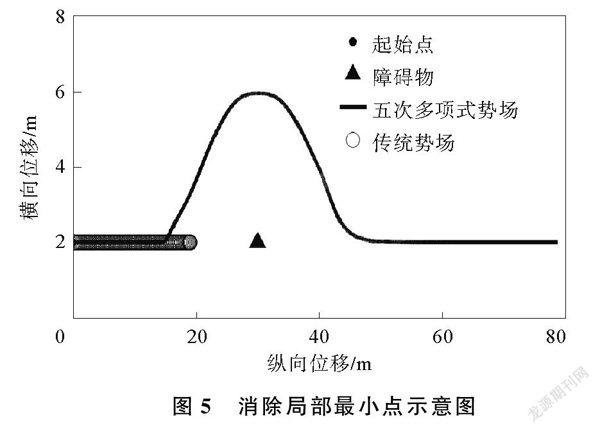
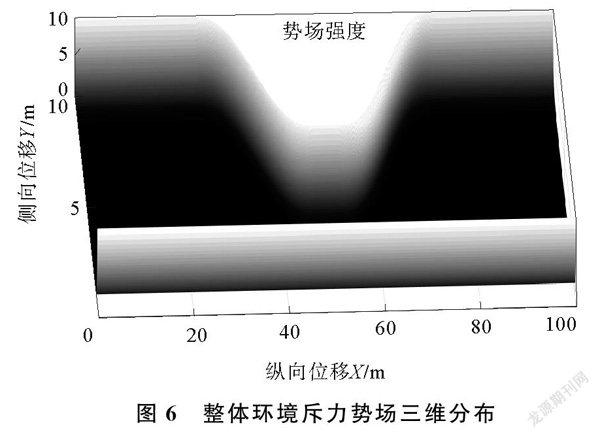
消除局部最小点示意图如图5所示。当汽车、障碍物与目标点三者共线时，传统人工势场法引力与斥力相抵，陷入局部最小点。改进后的势场模型中，汽车受到的势场斥力来自汽车右侧，消除了斥力与吸引力平行的情况，因此不会陷入局部最小点，能够顺利规划路径。改进后，整体环境斥力势场三维分布如图6所示。道路斥力势能从车道中心线开始随着沿车道边界距离的减小而增大，道路中心可通行区域势能为0。障碍物势场变化趋势与道路边界相同。障碍物势场边界与道路势场边界相连接，可将车辆避障和沿车道行驶统一视作车辆沿边界连续变化的道路行驶行为。

2仿真实验

利用Simulink与Carsim联合仿真验证所提算法进行汽车主动避障局部路径规划时的有效性。Carim是一种专业的车辆动力学仿真软件，目前已被企业和高校广泛的应用于汽车研发。以Carsim中的C级掀背车模型为测试对象，分别在平直道路上躲避前方障碍物、侧方行人和后方高速车辆。

对以上3种情形进行模拟。为保证汽车转向时的稳定、安全，车速和前轮转角之间存在特定关系，车速越高，前轮转角越小，因此，使用侧向加速度对汽车转向进行约束。当处于线性工况下，汽车行驶在附着系数良好的道路上，通常要求汽车转向时的侧向加速度不超过04 g[18]。针对车辆紧急转向避障工况，文献＼[19＼]进行了详细分析，认为在紧急工况下，汽车转向的侧向加速度应当约束在限制级和最大级之内。

限制级及最大级分别为

其中，v为汽车纵向速度;g为重力加速度;μ为路面附着系数。

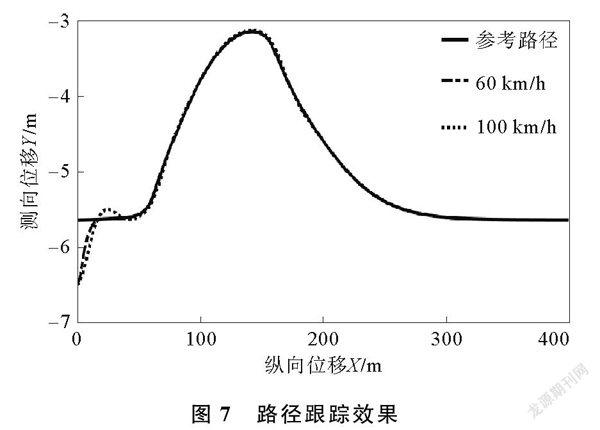
仿真基于Stanley方法设计路径跟踪控制器，Stanley方法是斯坦福大学在美国国防先进项目研究局组织的智能车挑战赛中提出的路径跟踪方法[20]，该算法具有计算简单、易于实现和实时性好的优点[21]。在Carsim中可以精确而迅速的控制车辆车轮转角，使用Stanley方法能够达到快速、稳定的路径跟踪效果。路径跟踪效果如图7所示，由图7可以看出，在不同车速下，路径跟踪控制器均能较为精确的跟踪目标路径。

参考行车安全性要求，结合各项研究中的专家学者经验[11]，设计仿真参数，经反复测试，改进算法使用的具体仿真参数如表1所示。

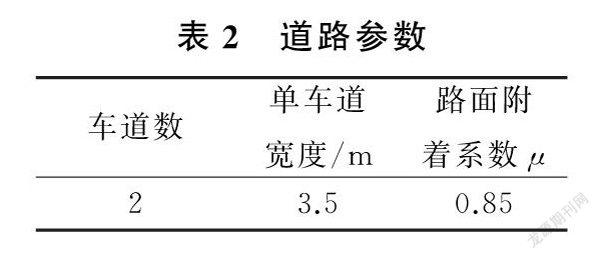
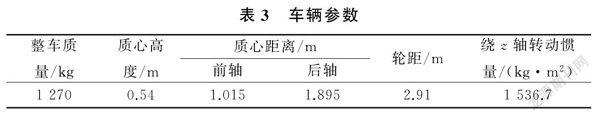
设计仿真场景为道路状况良好的城市双车道公路，避免车辆同车道并排和偏离车道等状况发生，设计车道宽度。同时，道路具有良好的摩擦系数，道路参数如表2所示。仿真车辆采用Carsim中的CClass Hatchback模型，从Carsim中获取车辆参数、速度、转向角等信息。CClass Hatchback模型为道路上常见的C级掀背车，以该模型作为仿真车辆具有典型性。车辆参数如表3所示。

2.1躲避前方两固定障碍物

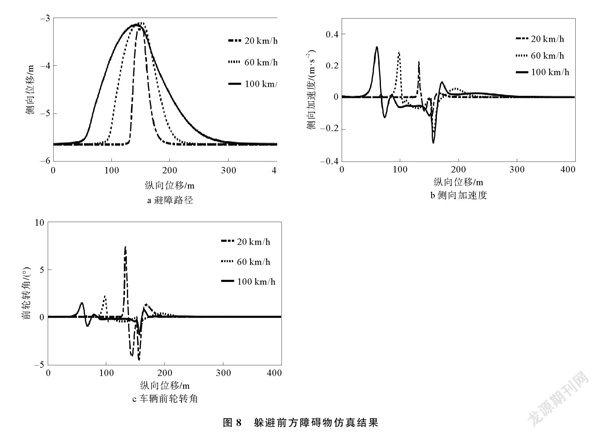
主车分别以20，60，100km/h的速度沿右车道中心线直线行驶，前方有两个固定障碍物，与主车初始位置纵向距离为150 m和200 m，横向距离为0和375 m。设置障碍物长5 m，宽2 m。躲避前方障碍物仿真结果如图8所示。由图8a可以看出，算法能够引导主车在不同车速下躲避前方多个固定障碍物。当车速为20和60 km/h时，避障路径变化趋势接近，避障纵向距离和避障横向距离随车速提高而增大。由图8b可以看出，当车速为100 km/h时，主车受到障碍物2的影响提前转向，侧向加速度峰值随车速增加增大，但仍保持在04 m/s2之内。主车在避障过程中一直处于正常工况内，行驶状态稳定。

2.2躲避侧方行人

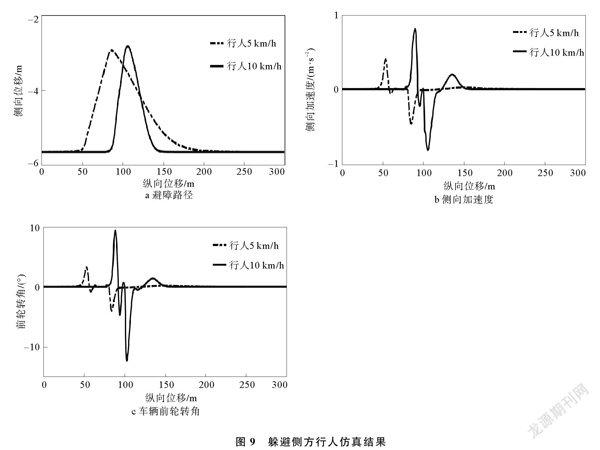
主车以60 km/h的速度沿右车道中心线直线行驶，前方行人与主车初始位置纵向距离为100 m，横向距离分别为83和166 m，分别以5 km/h和10 km/h的速度横穿道路，将行人视作质点，躲避侧方行人仿真结果如图9所示。由图9可以看出，算法能成功引导主车躲避侧方不同速度的行人。算法仅考虑道路范围内的障碍物，当速度为10 km/h的行人闯入道路时，主车与行人的距离已较为接近，所提算法仍能顺利引导主车避开行人。躲避侧方行人属于紧急工况下的避障，当行人速度提高至10 km/h时，主车侧向加速度峰值增大，但仍处于最大级范围内。

2.3躲避后方高速车辆

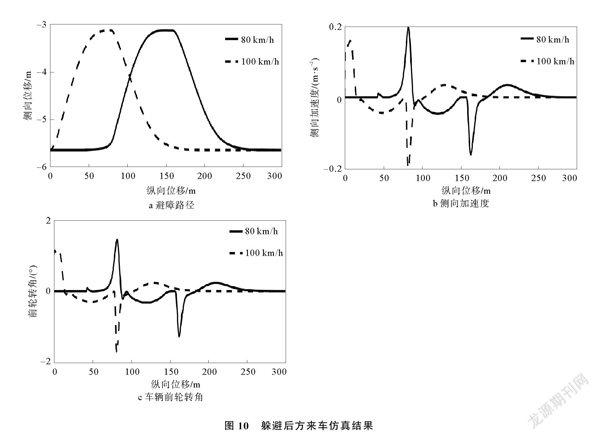
主车以60 km/h的速度沿右车道中心线直线行驶，后方障碍物与主车初始位置纵向距离为50 m，横向距离为0 m，分别以80 km/h和100 km/h的速度沿直线接近主车，设置障碍物长5 m，宽2 m。躲避后方来车仿真结果如图10所示，主车能够成功躲避不同速度的后方高速车辆，避免追尾事故发生。避障过程中综合考虑了主车车速和主车与障碍物之间的相对速度的影响，当后方有高速车辆驶来时，主车能够提前做出反应。

与图8躲避前方障碍物仿真结果相比，躲避后方动态障碍物时的避障纵向距离更长。当障碍车处于主车前方时，碰撞风险减小，主车在引力场的引导下迅速返回原车道。综上所述，汽车在结构化道路中躲避动、静态障碍物时，本文所提算法能够有效规划出避障路径，对于纵向障碍物的躲避效果较好。

3结束语

本文提出的基于改进人工势场法的避障局部路径规划算法，结合了五次多项式换道轨迹设计虚拟势场边界，综合考虑了汽车行驶速度与障碍物速度两个参数，设计了势场函数状态参数。仿真结果证明了所提出算法在不同工况下的路径规划能力，汽车在结构化道路中躲避纵向动、静态障碍物和侧向速度10 km/h以内障碍物时，算法能够成功规划避障路径，具有良好的鲁棒性。相对于传统人工势场法，规划出的路径满足汽车行驶安全和合法性的要求，改善了避障路径的平滑性，消除了传统人工势场法中存在局部最小值的问题，路径规划能力得到了明显提升。该算法能够实现汽车在结构化道路中高速工况下的避障局部路径规划，为实现无人驾驶技术提供了研究思路。但该算法仅考虑转向避障，未来将研究速度规划算法，进一步提高汽车主动避障能力。

参考文献：

[1]张家旭， 王欣志， 赵健， 等. 汽车高速换道避让路径规划及离散滑模跟踪控制[J]. 吉林大学学报（工学版）， 2021， 51（3）： 10811090.

[2]来飞， 叶心. 汽车高速行驶时自动紧急转向避撞的前馈与反馈跟踪控制的研究[J]. 汽车工程， 2020， 42（10）： 14041411.

[3]裴晓飞， 李朋， 陈祯福， 等. 不同紧急工况下的汽车主动避撞控制的研究[J]. 汽车工程， 2020， 42（12）： 16471654.

[4]李洪硌. 无人驾驶汽车高速工况智能决策、轨迹规划与跟踪研究[D]. 广州： 华南理工大学， 2020.

[5]张家旭， 王晨， 郭崇， 等. 基于自适应神经模糊推理系统的平行泊车路径规划[J]. 汽车工程， 2021， 43（3）： 323329.

[6]KHATIB O.  Realtime obstacle avoidance for manipulators and mobile robots[J].  The International Journal of Robotics Research， 1986， 5（1）： 9098.

[7]陈相茹. 基于人工势场理论的车辆行驶路径建模研究[D]. 长春： 吉林大学， 2020.

[8]GE S S， CUI Y J.  Dynamic motion planning for mobile robots using potential field method[J].  Autonomous Robots， 2002， 13（3）： 207222.

[9]王树凤， 张钧鑫， 刘宗锋. 基于改进人工势场法的智能车辆超车路径规划研究[J]. 汽车技术， 2018（3）： 59.

[10]唐志荣， 冀杰， 吴明阳， 等. 基于改进人工势场法的车辆路徑规划与跟踪[J]. 西南大学学报（自然科学版）， 2018， 40（6）： 174182.

[11]王其东， 魏振亚， 陈无畏， 等. 基于参数时变人工势场的车道保持协调控制[J]. 机械工程学报， 2018， 54（18）： 105114.

[12]刘翰培， 王东署， 汪宇轩， 等. 移动机器人路径规划的模糊人工势场法研究[J/OL]. 控制工程， 2021： 16. https：∥doi. org/10. 14107/j. cnki. kzgc. 20200187

[13]ZHOU Z Y， WANG J J， ZHU Z F， et al.  Tangent navigated robot path planning strategy using particle swarm optimized artificial potential field[J].  Optik， 2018， 158： 639651.

[14]豆祥忠. 基于改进人工势场法和栅格法的自主配送车避障研究[D]. 西安： 长安大学， 2019.

[15]SONG X L， CAO H T， HUANG J.  Vehicle path planning in various driving situations based on the elastic band theory for highway collision avoidance[J].  Journal of Automobile Engineering， 2013， 227（12）： 17061722.

[16]朱西产， 刘智超， 李霖. 基于车辆与行人危险工况的转向避撞控制策略[J]. 汽车安全与节能学报， 2015， 6（3）： 217223.

[17]北京市市政工程设计研究总院. CJJ 37—2012城市道路工程设计规范[S]. 北京： 中国建筑工业出版社， 2012.

[18]余志生. 汽车理论[M]. 北京： 机械工业出版社， 2009.

[19]王树凤， 张大伟. 车速与前轮转角的极限关系分析[J]. 机械设计与制造， 2017（S1）： 237240.

[20]THRUN S， MONTEMERLO M， DAHLKAMP H， et al.  Stanley： The robot that won the DARPA grand challenge[J]. Journal of Field Robotics， 2006， 23（9）： 661692.

[21]王亚平， 无人驾驶汽车轨迹跟踪控制研究[D]. 长沙： 湖南大学， 2015.

Research on Local Path Planning of Vehicles Active Obstacle Avoidance

Based on Improved Artificial Potential Field Method

FAN Sihana， ZHANG Hongxina，b

（a. College of Mechanical and Electrical Engineering; b. Power Integration and Energy

Storage Systems Engineering Technology Center， Qingdao University， Qingdao 266071， China）

Abstract：  Aiming at the problems of planning ability insufficient of active obstacle avoidance， path smoothness insufficient and easy to fall into local optima when artificial potential field method is applied to structured roads， this paper proposes a path planning algorithm that combines artificial potential field method and the quintic polynomial function obstacle avoidance trajectory to meet the safety and realtime requirements of automobile obstacle avoidance.  By introducing the quintic polynomial function potential field boundary and designing boundary parameters based on the motion states of the car and the obstacle， the smoothness and safety of the path are improved.  By setting the followmove target point to optimize the attractiveness model and the adjustment factor to optimize the potential field function， the local minimum point is eliminated.  It uses Carsim/Simulink to build the simulation environment， and uses the Stanley method to path tracking.  The simulation results show that the proposed algorithm can effectively plan obstacle avoidance paths that satisfy the requirements of vehicle driving in both dynamic and static environments.  This algorithm provides a reference for local path planning in vehicle collision avoidance.

Key words： intelligent vehicles; active obstacle avoidance; path planning; artificial potential field method

收稿日期： 20210816; 修回日期： 20211109

基金項目：  国家自然科学基金资助项目（52075278）; 青岛市民生科技计划资助项目（196192nsh）

作者简介：  范思汉（1996），男，硕士研究生，主要研究方向为电动汽车智能化动力集成技术。

通信作者：  张洪信（1969），男，博士，教授，主要研究方向为电动汽车智能化动力集成技术。Email： qduzhx@126.com