曲线回归在火灾经济损失中的应用
2022-03-24王林
王 林
(应急管理部消防救援局昆明训练总队,云南 昆明 650000)
0 引言
火灾的直接经济损失包括火灾造成的人员伤亡、物质破坏的经济损失以及救火过程中投入的各项费用。据统计,我国平均每年因火灾导致的直接经济损失达数十亿元,特别是2013年,我国火灾直接经济损失高达40多亿元。例如2014年我国发生了395 052起火灾,死亡人数1 815,受伤人数1 513,直接经济损失470 234.4万元。因此,研究火灾起火原因,总结经验教训,减少经济损失,也是对国家经济作出贡献的方法之一,本文主要使用曲线回归分析方法对火灾带来的经济损失进行预测研究。
曲线回归(curvilinear regression)是指对于非线性关系的变量进行回归分析的方法。曲线回归方程包括指数函数曲线方程、幂函数曲线方程和Logistic曲线方程等,一般是以自变量的多项式表达因变量。方法是根据已知数据的特点先进行平方根变换或者对数变换,变换后如果得到曲线模型,则用曲线拟合的方法对原始数据进行拟合,确定曲线回归方程。本文参照中国消防救援年鉴,截取1979—2018年的火灾直接经济损失数据,以年份为横轴,经济损失为纵轴绘制散点图,根据散点图趋势,结合常见图形的形状和专业知识,选定几种可能性大的曲线类型,找出与经济损失原始数据散点拟合程度最高的曲线函数类型,以直接经济损失作为因变量,年份作为自变量构建预测模型。
1 数据来源
本文数据来源于中国消防救援年鉴,记录了1979—2018年度统计所有直接经济损失的火灾事故调查报告。并且规定1979年为基准年,取值T=1,2018年T=40,根据以上数据建立火灾直接经济损失数据统计表,如表1所示。

表1 1979—2018年火灾直接经济损失数据统计表
2 绘制散点图
根据以上年份T和火灾直接经济损失K的统计数据,运用EXCEL绘制出(T,K)的散点图,如图1所示。

图1 年份与经济损失散点图
3 构建回归模型
根据年份T和火灾直接经济损失K的散点图分布趋势可知,自变量和因变量之间不存在线性关系,因此只能选择曲线函数模型。结合指数曲线函数图形的构成形状可以考虑用指数函数模型,指数函数模型表达式:K=αeλT
结合表1,通过运用SPSS软件,可以得到直接经济损失Κ和年份Τ曲线拟合图及模型汇总表、ANOVA表格、回归系数汇总表,并建立指数函数模型。
经济损失Κ和年份Τ的曲线拟合图如图2所示。
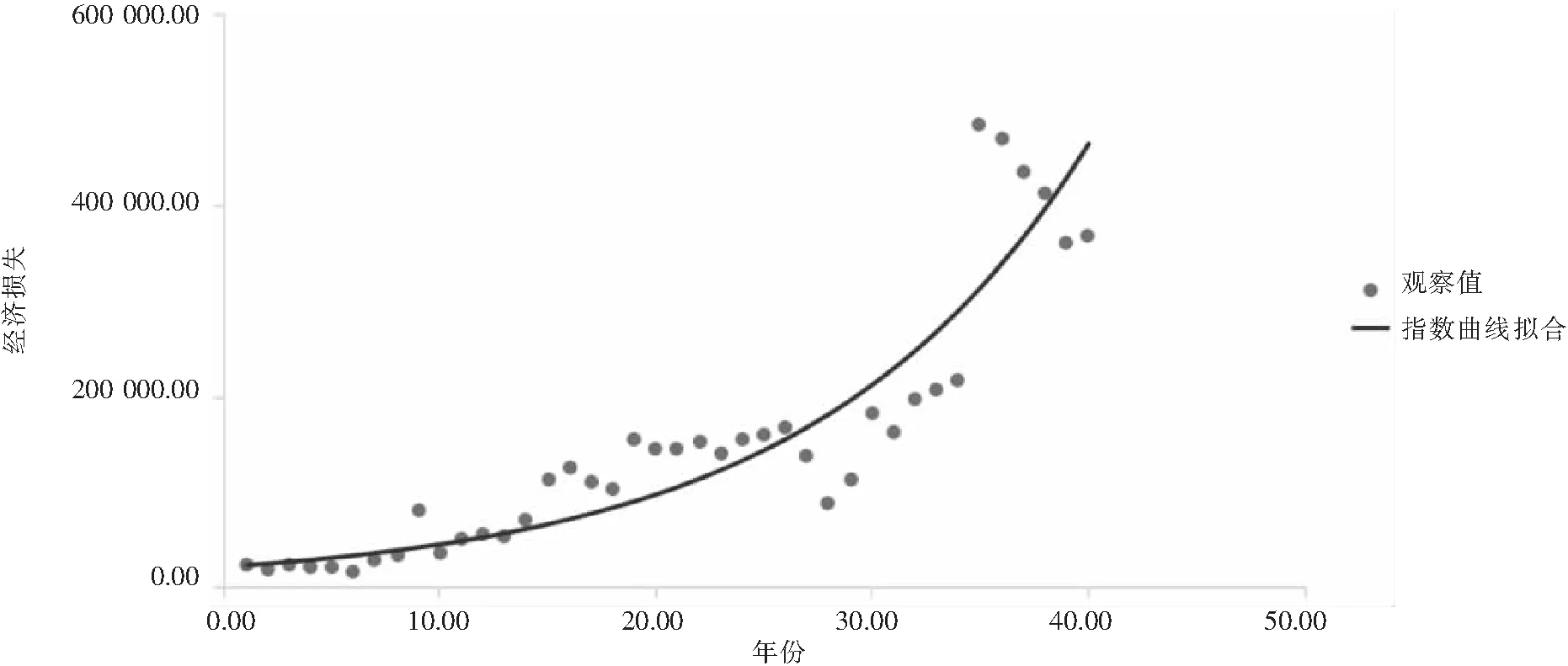
图2 年份和经济损失指数曲线拟合图
从经济损失和年份曲线拟合图可以看出,它们之间确实呈现指数拟合关系。
由模型汇总表(见表2)可知,模型R2=0.877,调整后的R2=0.874与R2差距很小,而且还大于0.5,表明自变量能较好地测算因变量的变化,即模型拟合程度较高。从ANOVA表格(见表3)可知,ρπ0.01,表明模型通过F检验,即模型是合理的且呈现出0.01水平的显著性差异。根据回归系数汇总表(见表4)可知,模型公式如下:

表2 模型汇总

表3 ANOVA表格

表4 回归系数汇总表
lnK=9.907+0.079×T
经整理可得下面指数函数模型:
K=20 070.372e0.079T
其中,K表示直接经济损失,T表示序号。
4 分析
本文根据我国火灾直接经济损失数据,借助SPSS软件,得到了火灾直接经济损失K和年份T的曲线拟合图及指数函数模型,模型通过F检验且呈现出0.01水平的显著性差异,同时回归系数值为0.079,表明随着年份T的增大,火灾直接经济损失K呈现出指数曲线上升。
5 结语
火灾的发生因素较为复杂,对灾后进行经济损失评估考虑的因素也众多。本文通过绘制(T,K)的散点图,找出与经济损失原始数据散点拟合程度最高的非线性回归指数函数模型,并通过建立的模型进行回归分析和预测,根据回归分析可知火灾直接经济损失与年份有较强的相关性,因此文章能够通过建立的指数函数模型预测未来我国火灾直接经济损失的发展趋势。
