基于互信息和MPCA的单基药塑化过程监测方法
2022-03-24杨明毅王军义白鑫林徐志刚余廷江陈舒渤
杨明毅,王军义,白鑫林,徐志刚,余廷江,陈舒渤
(1.中国科学院 沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2.中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169;3.中国科学院大学,北京 100049;4.泸州北方化学工业有限公司,四川 泸州 646003)
塑化过程作为单基发射药生产过程的重要工序,对其成型和产品质量起着至关重要的作用[1-2]。但目前塑化过程缺乏微小幅值的渐变式故障检测和异常工况的监测预警,致使单基药的生产运行存在巨大的安全隐患。
以多向主成分分析(MPCA)[3]为代表的统计过程监测方法[4]为塑化过程监测提供了新思路。但MPCA及其多种改进策略[5-7]仍为线性建模方法,后续又有学者提出多向核主成分分析(MKPCA)[8-9]等多种非线性监测方法[10-11]。本文提出一种基于归一化互信息的多向主成分分析方法。其在建模时充分体现了变量间的相关性差异,具有更好的监测能力,可实现塑化过程的故障检测和运行工况的异常监测与早期预警。
1 基本理论与方法
1.1 单基药塑化工艺过程及其批次过程属性
单基发射药本质为含硝化棉的溶塑火药,通常采用溶剂法挤压成型工艺进行制备。其主要原材料为两种含氮量不同的硝化棉组成的混合棉和少量的安定剂(二苯胺)等。单基药塑化过程工艺流程图见图1,采用乙醇和乙醚构成的醇醚溶剂溶解硝化棉,利用缸式捏合塑化机使含硝化棉的药料转变为混合均匀且结构致密的胶状可塑性药料,以便后续的成型工序。塑化机通过一对搅拌浆的相对转动,使药料之间受到相互摩擦、挤压、撕裂拉伸等作用,从而使药料捏合塑化。其过程的基本操作流程可描述为:进料→塑化加工→等待出料→完成出料→清洗→等待进料。塑化过程工艺参数主要包括:组分含量及比例、塑化温度、塑化时间、搅拌力和搅拌速度等。目前,药料塑化的质量效果仍需工艺人员现场评估,使其过程安全性显得更为重要。
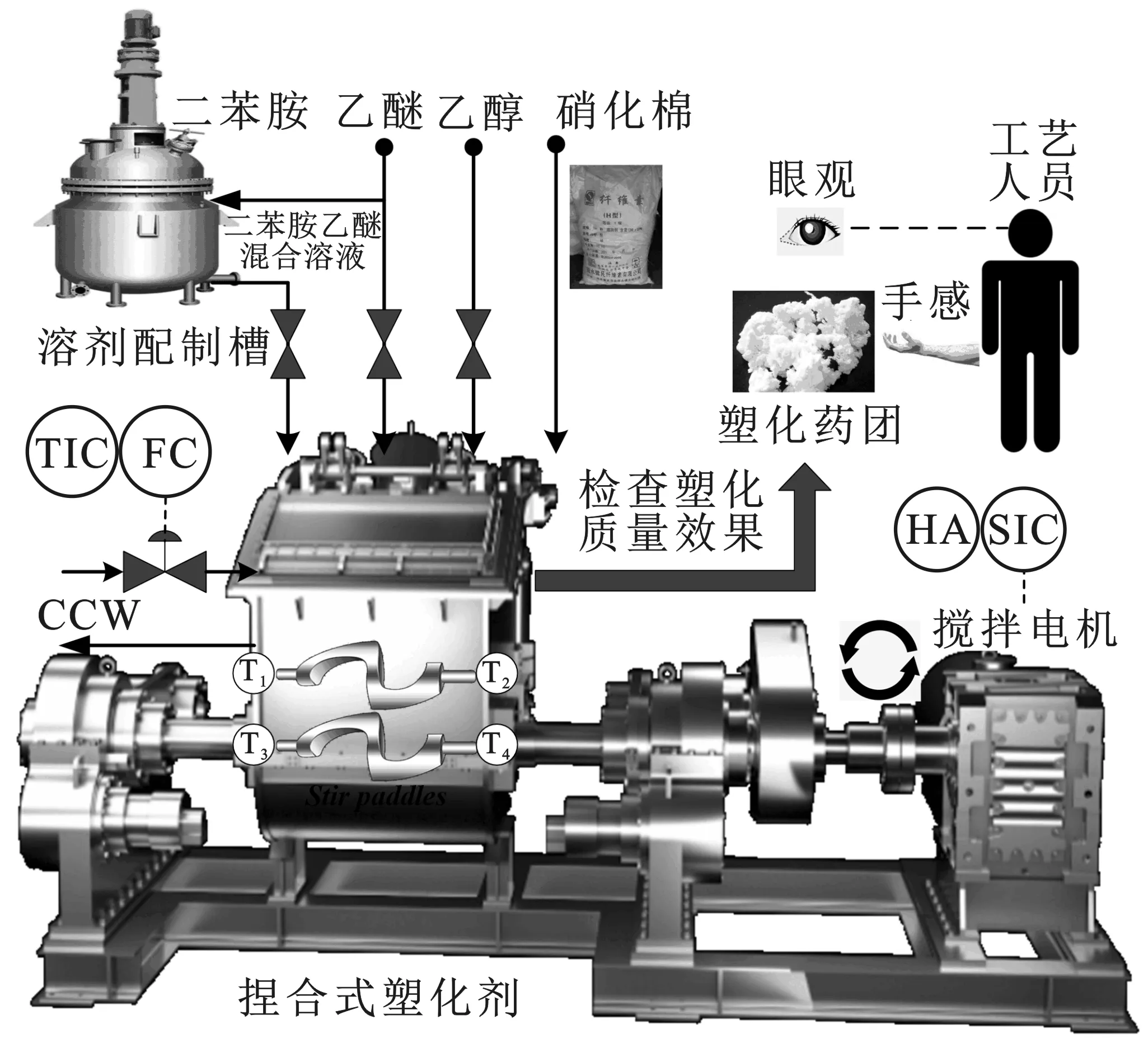
图1 单基药塑化过程工艺流程图
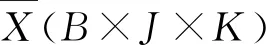
1.2 基于多向主成分分析(MPCA)的过程监测方法
主成分分析(PCA)是一种基于多元投影的线性降维方法,其主要思想是将高维度空间转化为低维度空间,并尽可能保留高维度的信息。假设过程中有m个传感器采集,每个传感器进行n次采样,则构成数据矩阵X=[x(1),x(2)…x(n)]T∈Rn×m,PCA模型将X分解为:
(1)
T=XP
(2)
(3)
(4)

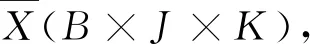
MPCA仅需正常操作工况下的变量测量值作为建模数据,其反映的是一种过程变量间的交叉相关性及变量自身的自相关关系。当过程出现异常时,导致过程变量的运行轨迹或变量间的耦合相关关系发生变化时,监视MPCA模型的多元统计量Hotelling-T2和平方预测误差(SPE)控制图[3,13]是否超限可检测到故障的发生。通过累计方差贡献率或交叉验证法确定主元个数为A,T2统计量定义如下:
T2=[t1,t2…tA]Λ-1[t1,t2…tA]T
(5)
(6)
监测过程故障是否发生的T2统计量控制限服从F分布:
(7)
SPE统计量定义如下:
(8)
SPE统计量的控制限采用权重系数(g)和自由度(h)的估计方法来确定:
(9)
(10)
其中,vk、mk分别为建模数据集中第k时刻的平方预测误差的均值和方差。
2 NMI-MPCA算法
为了更好地处理过程中包含的多种线性与非线性关系混合特征,并体现不同维度变量间耦合相关性的差异,本文提出一种基于归一化互信息的多向主成分分析(NMI-MPCA)故障检测方法。其主要包括批次过程数据的双阶段展开、多维变量耦合关系刻画与加权修正建模、多模型监控信息融合三个部分。
2.1 塑化过程批次数据的双阶段展开方法
理想情况下,塑化过程各个批次数据应是运行相同时长的,但实际单基发射药塑化过程受原材料波动、塑化效果难评价以及干扰等不同方面的影响,导致塑化过程各批次数据的时间长度基本均不相同,有时还存在较大差异。而沿批次方向展开较难处理批次不等长问题,且在线应用时需对未来时刻值进行估计填充,容易引入误差,降低模型的监控性能。沿变量方向展开则忽略了不同时刻间变量间的相关性,无法消除过程变量时间轴上的非线性,致使其对故障不敏感,导致故障检测的快速性和灵敏性较差。
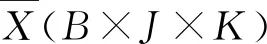

图2 塑化过程数据双阶段展开方法示意图
2.2 基于归一化互信息的耦合关系刻画与加权修正建模
在概率论和信息论中,互信息是度量两个随机变量之间统计相关性的信息量,其衡量的是变量间共同拥有的信息,能同时评估两个变量之间的线性相关性和非线性相关性程度[13-14]。
对于两个离散变量x和y,其互信息I(x;y)定义为:
(11)
其中,p(x,y)为两个随机变量x和y的联合分布,p(x)和p(y)分别为边缘概率。 若x和y之间相互独立,即不存在任何重叠信息时,其互信息值等于0。 反之,若两者间相关性越高,则互信息值越大。 由式(11)可知,互信息的求解需要已知变量x和y的概率密度分布。 由于没有数据分布的先验知识,本文采用文献[15]中的核密度估计方法拟合出其概率密度,确定变量对应的概率值。
为便于后续的加权修正运算,本文将互信息进行归一化处理,其计算公式为:
(12)
其中,NMI(Normalized Mutual Information)即归一化互信息,H(x)和H(y)分别为x和y的信息熵,是表示变量取值不确定性程度的指标。x的初始不确定度可以用熵H(x)表示:
(13)
归一化互信息之所以采用(H(x)+H(y))/2作为分母,是因为它是互信息I(x;y)的紧上界,因此可以保证NMI∈[0,1]。
加权修正建模为先通过归一化互信息刻画批次过程中多维变量间的复杂耦合作用关系,然后以此对不同维度变量之间的相关性特征进行加权修正,得到充分体现每个变量与其他维度变量之间耦合作用关系的数据集,再分别建立与其相应的MPCA状态监测模型,具体实施方法及步骤见3.1节。
2.3 基于贝叶斯推理的多模型信息融合策略
NMI-MPCA建立了J种不同的MPCA模型,在线应用时新样本将同时被J个MPCA模型监测,会得到J组不同的统计量信息,任何一组统计量超限都代表过程可能进入非正常的工作状态,这将导致监测模型过于敏感,增加系统误报警的概率。为此,本文采用贝叶斯推理策略[16]整合所有MPCA模型的信息,将多个MPCA的统计量指标融合为一组概率型指标。
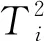
(14)

(16)
(17)
本文中置信限α统一取值为99%。 最后,按照加权融合形式得到全局统计量指标BIST2。
(18)
同理,对SPE统计量采用贝叶斯推理进行融合,可得到BISSPE。 当BIST2>1-α或BISSPE>1-α时,过程被认定为异常状态。 否则,过程处于正常工作状态。
3 基于NMI-MPCA的过程监测方法
NMI-MPCA通过J种不同的方式,对塑化过程的批次数据进行加权修正,以体现不同变量维度与其他维度之间的相关性差异,并相应建立J个 MPCA 模型。同时,对新批次数据进行在线监测时需对其进行同样的加权修正策略,然后再调用每个MPCA 模型计算相应的统计量。NMI-MPCA算法流程具体包括离线建模和在线监测两部分。
3.1 建立正常工况下的NMI-MPCA模型(离线建模)
(1)三维数据展开,采集正常工况下塑化过程的批次数据作为训练数据集,将三维数据集按本文所提方法进行展开,得到Xtrain(BK×J)。
(2)耦合关系刻画,针对第i(i=1,2,…J)维过程变量xi,计算其与Xtrain中各维变量xk(k=1,2,…J)间的归一化互信息值NMI(xi;xk)。
(3)加权修正,根据计算得到的归一化互信息数值大小确定对应于第i维变量的权值向量ωi,其计算公式为:ωi=diag[NMI(xi;x1),NMI(xi;x2)…NMI(xi;xJ)],并对展开后的数据矩阵Xtrain(BK×J)进行加权处理,得到体现该维度变量与其他维度相关性差异特征的训练数据矩阵Xi=Xtrain×ωi。

(5)重复步骤(2)~步骤(4),得到J个加权处理后的数据集{X1,X2…XJ},并建立相应的J个 MPCA 状态监测模型。
(6)基于置信度(α)确定贝叶斯推理构造的全局统计量BIST2和BISSPE,控制限为1-α。
3.2 NMI-MPCA模型的在线故障监测
(1)在线监测新批次过程数据xnew,利用建模数据均值和标准差对新数据进行标准化处理。
(2)利用建模时得到的权值向量ωi(i=1,2…J)将新批次数据进行加权融合处理,即xnew,i=xnew×ωi,得到相应的xnew,1,xnew,2…xnew,J。
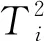
(4)通过贝叶斯推理构造新的全局统计量BIST2和BISSPE,将J组MPCA模型的统计量信息融合为一组概率型指标,若超出控制限则表示过程出现故障。
4 塑化过程应用研究
本文利用泸州北方化学工业有限公司某品号单基发射药的真实塑化过程数据进行应用研究。其中,塑化过程建模数据的操作条件见表1。用于建模的过程变量参见表2,共选取塑化过程的10个过程变量进行监测。通过团队为其研制的单基药生产过程控制系统(DCS),并结合人工干预等措施,共模拟产生了四种典型故障工况下的塑化过程批次数据,用于验证基于NMI-MPCA的故障检测算法,并与传统MPCA和MKPCA方法的监测性能进行对比。具体故障工况见表3,前三种为单一过程变量的波动而引发的故障,最后一种为原材料配比失调引起的运行工况异常。
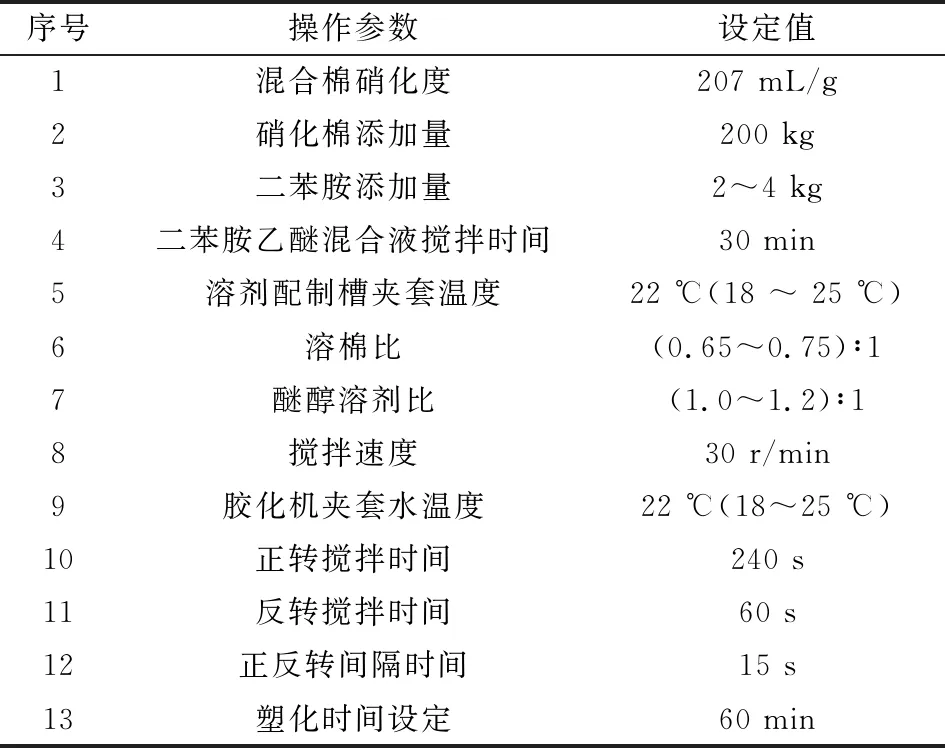
表1 塑化过程操作条件设定

表2 塑化过程建模使用的过程变量

表3 塑化过程引入的故障列表
该品号单基药各批次的塑化时间设定值为 60 min,但为保证塑化效果,需在工艺时间达到前,对药团进行开缸取样检查,由工艺人员现场对塑化效果进行评估,并给出继续塑化时间的设定值,因此导致每个批次的运行时间基本都不相同。本文共采用18个长度不等的批次数据作为训练数据集,建立MPCA,MKPCA和NMI-MPCA监控模型。以2个批次的正常数据和4个批次的故障数据作为测试数据集。单个批次的采样间隔为10 s,用于建模的各批次数据长度从60 min至1 h 26 min长度不等。置信限α取值统一设为99%,各MPCA 模型的主成分个数A均按照累计方差贡献率≥90%确定。由于传统的MPCA和MKPCA方法要求批次数据长度相等,因此建模时将18个批次长度全部截断为 60 min。显然,对于运行时长超过60 min的塑化过程,MPCA和MKPCA将无法进行过程监测。其中,MKPCA的建模方法与核函数选取等见文献[9]。
4.1 过程变量故障检测结果和分析
单基药DCS系统采用PCS7 V9.0开发,利用该平台对过程中的关键变量设定值叠加阶跃和斜坡等信号作为扰动,以模拟生成表3中的前三种故障工况。故障批次F1和F2分别为搅拌速率(x2)在 30 min 引入幅值为5%的跳变型故障和变化速率为0.1 r/min的渐变型故障直到过程结束。故障批次F3为胶化机夹套水温(x4)在30 min引入变化速率0.1 ℃/min的渐变型故障直到过程结束。
本节只列出故障批次F2的状态监测图,其他故障批次的监控结果可参见表4和表5。表4是三种方法对故障批次F1、F2、F3的误报警率比较。表5是三种方法对四个故障批次故障检出采样点的统计对比。
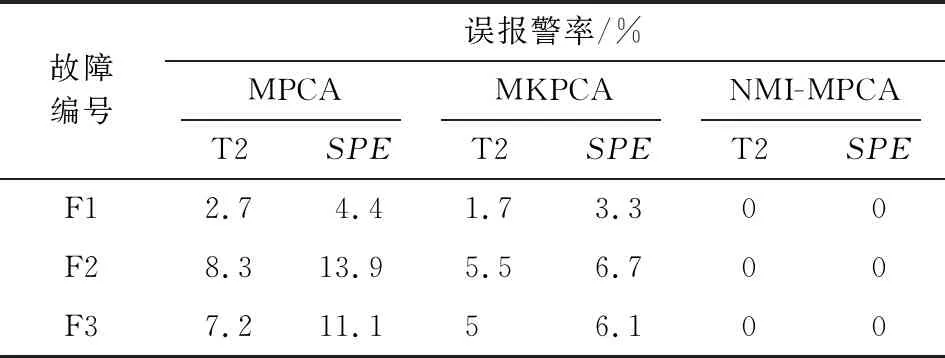
表4 三种方法对前三个故障批次的误报警率比较

表5 三种方法对四个故障批次的故障检出采样点比较
由表5可知,SPE的监测性能均优于T2统计量,因此以下仅给出各方法的SPE监测图。图3~图5分别为采用传统MPCA、MKPCA和本文NMI-MPCA算法对故障批次F2的监测结果。

图3 传统MPCA方法对故障批次F2的SPE监测图

图4 MKPCA方法对故障批次F2的SPE监测图
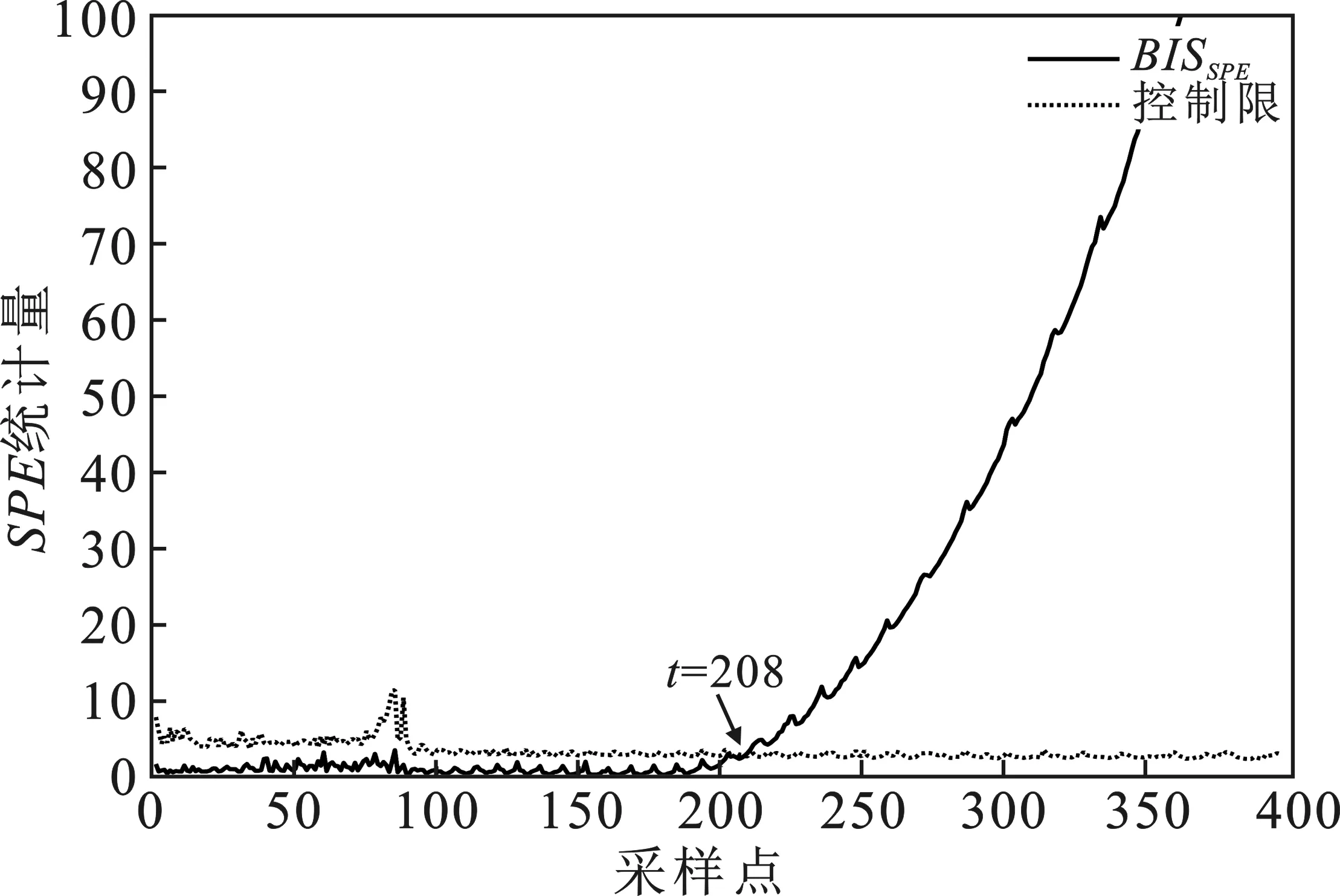
图5 NMI-MPCA方法对故障批次F2的SPE监测图
由图可知,①对于非故障时段(1~180采样点),MPCA 和MKPCA方法均有较高误报,有多点超出控制限,SPE统计量分别达到13.9%和6.7%的误报率(见表4)。这主要是由于MPCA 和MKPCA需通过当前值来估计过程的未来输出值,使其对波动数据过于敏感,从而增加误报警率。同时,塑化过程的批次操作,导致每批生产前胶化机的过程初始状态均不相同,在塑化前期更易导致误报警。而NMI-MPCA则很好地避免了该问题,有效降低了过程误报,由表4可知,其对前三个故障批次的均未出现误报警;②对于故障时段(180采样点之后)三种方法的T2和统计量,均在一定时刻超过控制限并不断增加,表明渐进型故障的发生。对比SPE统计量,NMI-MPCA的BISSPE在第208采样点便稳定超限,相当于在该渐变故障引入仅280 s即给出故障预警,分别领先MPCA和MKPCA方法74个和24个采样点提前给出故障指示。NMI-MPCA的BIST2统计量检测故障能力虽稍逊于BISSPE,但远优于MPCA和MKPCA方法的T2统计量。这表明在过程变量运行轨迹偏离正常工况的初期,传统MPCA和MKPCA方法建立的塑化过程监测模型不能快速识别出故障;③故障批次F2实际运行时长为66 min,共396个采样点,对于超出60 min的时间段,MPCA和MKPCA无法实现过程监控,而NMI-MPCA则在建模时通过双阶段展开方法解决了该问题,在超出时间段期间若发生故障其仍能及时给出故障警报。
由上可知,本文的NMI-MPCA方法监控性能优于传统MPCA和MKPCA方法。对于生产中常见的微小幅值渐变型故障,传统的变化率超限策略无能为力,只能通过设置报警阈值进行报警。目前DCS上设置的搅拌速率(x2)和胶化机夹套水温(x4)报警阈值分别为33 r/min和25 ℃,需要在60 min时才能报警。而采用本文的NMI-MPCA方法,则可在故障仅发生大约4 min后实现早期的故障预警,提前26 min检出故障,方便操作人员及时做出决策调整生产,使过程回到正常工作状态。
4.2 原材料配比失调的监测结果和分析
为验证本文所提方法对运行工况的异常监测和评价能力,设计了原材料配比失调这一故障工况进行试验,该故障会影响塑化效果,进而引起质量波动。塑化过程中,醚醇混合溶剂在单基药料中的含量会影响单基药料的流变性能。溶剂含量适中时,经塑化成型的药条组织均匀致密且表面光滑,无硬料和白斑等瑕疵。如果溶棉比例失调,会引起塑化质量效果的波动。溶剂含量较低容易导致药料流动性变差,成型压力过大,药条会出现白斑等不合格现象,且生产危险性提高;溶剂含量过高,硝化棉会过度溶解,在成型过程中无法达到组织均匀致密的要求。为保证塑化质量效果,溶棉比一般需保持在 (0.65~0.75)∶1之间。故障批次F4为在溶棉比设置为0.55∶1的条件下开始塑化操作,以模拟原材料配比失调故障,其运行时长为64 min。
由过程机理可知,当剪切速率不变而溶剂含量增加时,单基药料的表观粘度会随之下降。反之,溶剂含量降低,则使表观粘度增加,使得在塑化过程产生更多的剪切热,导致过程变量的运行轨迹和多维变量间的耦合关系偏离正常工况。此处仅给出NMI-MPCA算法对故障批次F4的监控结果,见图6。

图6 NMI-MPCA方法对故障批次F4的SPE监测图
由图6可知,NMI-MPCA算法的监控结果运行平稳,且能快速识别过程的异常工况,其BISSPE在第32采样点便稳定超限,相当于在过程运行仅 5 min 后即可给出故障预警。结合表5可知,其分别领先MPCA和MKPCA方法147个和97个采样点提前给出故障指示,工艺人员可及时发现该批次塑化药料存在异常并采取补救措施,从而避免影响单基药最终产品的质量。
5 结束语
针对单基药塑化过程提出一种基于归一化互信息的多向主成分分析故障检测方法,其可充分挖掘并建立多维变量间的复杂耦合作用关系模型,实现了多种故障的快速检测和异常工况的早期预警。便于操作人员及时采取相应措施,从而减少质量波动并提高过程的安全性;同时该方法有效降低了故障检测的误报警率,减少了由此引起的生产中止和故障排查时间,从而提高生产效率。
