粒子群优化算法在堆石坝材料参数反演中的应用

孙 丹，焦 洁，梁 艳，李 帆

(河海大学设计研究院有限公司，江苏 南京 210098)

在利用有限元计算堆石坝应力和变形时，堆石坝材料参数选取的准确与否，直接关系到数值计算的精确度。因此，有必要将原型实测位移资料作为依据，通过相应的理论分析，反演堆石坝的材料参数。粒子群优化算法于1995年由J.Kennedy等人提出，该法概念明确，原理简单，使用的参数少，已经被证明是一种收敛性很强的优化算法；粒子群优化算法中的粒子具有记忆特性，粒子通过自我认知和向他人学习改变自身的速度和位置，从而在较短时间内找到全体最优解。

1 粒子群优化算法

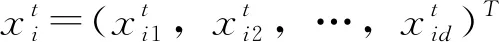
(1)

(2)

式中，i—粒子序号(1≤i≤m)；j—某一待反演材料参数(1≤j≤d)；w—惯性权重；c1、c2—学习因子；r1、r2—随机数，在(0，1)范围内均匀分布。

2 基于粒子群优化算法的堆石坝材料参数反演

2.1 反演参数的选择

堆石坝在有限元计算程序中采用邓肯-张E-B本构模型，共有8个待定参数，分别为K、n、Rr、Kb、m、Kur、C和φ。对于堆石料，C一般取为0，Kur与K具有相关性，取一个参数即可。对剩下的6个变量K、n、Rr、Kb、m、φ进行敏感性分析，通过正交试验分析表明，K、n、Kb、m这4个参数对位移敏感性相对较强，其他参数的敏感性相对较弱。因此，最终确定待反演参数个数为4i为Ki、ni、Kbi、mi，其中i为堆石坝堆石料的种类数。

2.2 反演模型

利用堆石坝已有的位移实测值，对材料参数进行反演分析，最终使位移计算值与位移实测值接近，以获得材料参数。当采用有限元法计算时，基于位移实测值的反演模型如下：

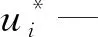
2.3 反演步骤

基于粒子群优化算法的堆石坝材料参数反演的具体步聚如下：

(1)首先需要确定待反演参数的总数(即维数d)以及粒子群优化算法的各计算参数(包括粒子群总数m、惯性权重w、学习因子c1和c2)；同时，根据设计时材料的试验数据及工程经验给定待反演参数的取值范围，以限制待反演参数在各自的取值范围内运动；

(2)赋予m个粒子初始的位置和速度，粒子位置代表待反演材料参数的具体数值；

(3)将每个粒子的位置作为个体最好位置，存储于pi(i=1，2，…，m)中；然后根据每个粒子的位置，按公式(3)计算适应值函数F(x)，将使得F(x)值最小的粒子位置作为全体最好位置，存储于pg中；

(4)根据公式(1)、(2)，对所有粒子的位置和速度进行第一步迭代更新；

(5)对上一步迭代更新后的每一个粒子，按公式(3)计算自身的适应值函数F(x)，并将计算所得的F(x)与该粒子到目前为止所经历过的个体最好位置的F(x)进行比较，取F(x)较小值所对应的粒子位置作为该粒子的个体最好位置，更新pi。然后，比较本步骤中所有粒子的个体最好位置对应的F(x)大小，找出全体最好位置，更新pg；

(6)当最大迭代次数或者收敛精度其中之一满足时，终止迭代，并输出全体最好位置pg作为反演参数值；否则，返回步骤(4)。

3 工程实例

3.1 工程概况

某混凝土面板堆石坝，最大坝高为136.5m，坝顶宽度为11m，迎水坡坡比为1∶1.4，背水坡平均坡比为1∶1.5，堆石坝横断面如图1所示。

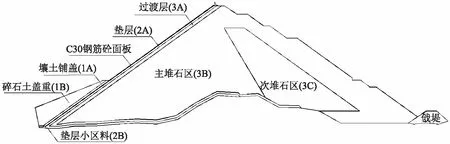
图1 堆石坝横断面图

为了监测大坝在施工期和运行期的工作情况，在坝体内埋设了多种监测仪器，其中水管式沉降仪共布设了6条，共36个测点，位于坝横0+57.5和坝横0+105.5两个代表断面上，如图2—3所示(图中“ES”为水管式沉降仪的编号)。

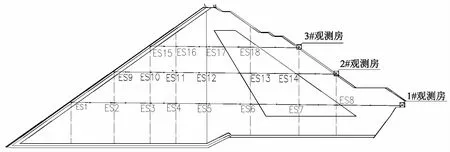
图2 坝横0+57.5断面监测点布置图

对坝体及一定范围坝基进行有限元网格剖分，将所有的监测点均安排到有限元结点上，单元采用6面体8结点等参单元，剖分单元的大小为水平向8～14m，垂直向5～10m。离散后，坝体和一定范围坝基有限元网格结点数为4960，单元总数为4531。

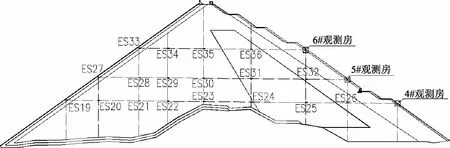
图3 坝横0+105.5断面监测点布置图

3.2 反演结果及分析

为了使反演结果准确反映大坝工作性态，本文选择具有代表性的ES21和ES25测点，同时，分析施工期和运行期两种工况。

由图2看出，混凝土面板堆石坝主要材料分为主堆石区(3B)、次堆石区(3C)两种，由此确定堆石坝材料待反演参数的个数为8个，分别为主堆石区(3B)的K1、n1、Kb1、m1和次堆石区(3C)的K2、n2、Kb2、m2。根据设计时材料的实验数据以及工程经验，确定8个参数的搜索范围见表1。

表1 堆石坝材料反演参数取值范围

本工程堆石坝采用粒子群优化算法进行反演计算的主要控制参数如下：粒子群总数取20，迭代次数取100，学习因子c1取1.5，c2取2.0，惯性权重w取0.5。

最终得到的该坝堆石坝材料参数反演结果见表2。为了检验反演结果的合理性，表3列出了ES21及ES25测点在施工期和运行期两种工况下位移实测值与计算值的对比情况。从表3可以看出，相对误差较小，均控制5%以内，说明粒子群优化算法用于堆石坝材料参数反演中是合理可行的。

表2 堆石坝材料反演参数结果

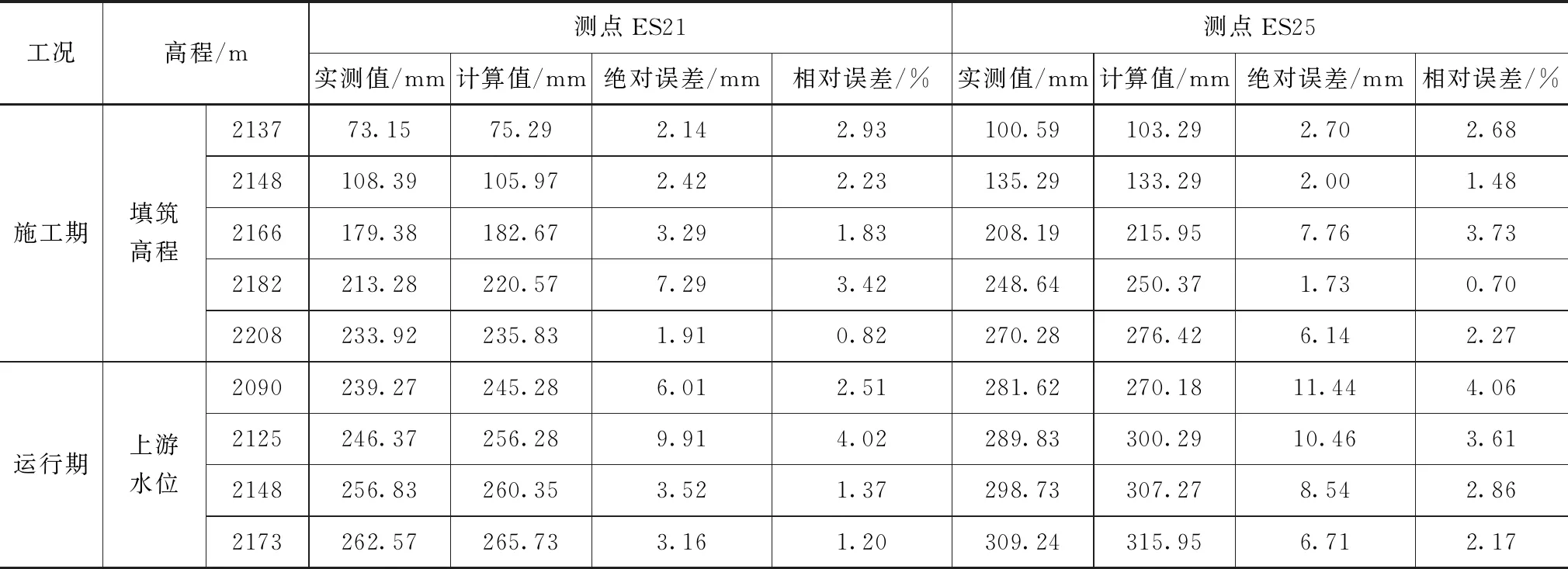
表3 测点ES21、ES25位移实测值与计算值对比表

4 结语

粒子群优化算法作为一种智能方法，具有概念简单、程序容易实现等优点，本文以某混凝土面板堆石坝实测位移为基础，确定堆石坝材料的待反演参数，建立邓肯-张E-B本构关系的堆石坝有限元模型，提出位移计算值和实测值的适应值函数，采用粒子群优化算法不断调用有限元模型，得到待反演参数。计算表明，采用粒子群优化算法得到的位移计算值与实测值的相对误差在5%以内，因此，粒子群优化算法用于堆石坝材料参数反演中是合理可行的，该研究成果在堆石坝的变形分析中具有一定的参考价值。