一种超像素上Parzen窗密度估计的遥感图像分割方法
2022-03-24张大明张学勇李璐刘华勇
张大明, 张学勇, 李璐, 刘华勇
(1.安徽建筑大学数理学院,合肥 230022; 2.安徽省建筑声环境重点实验室,合肥 230601)
0 引言
高分辨率多光谱影像能提供几何形状、光谱和纹理等丰富的地物信息,对地物目标识别精度的提高有很大帮助。现在,已经有许多卫星能够提供米级和亚米级的高分辨率遥感图像,它们在农业、采矿、防灾减灾和环境调查等各个领域中有广泛应用[1-3]。图像分割是指将图像分割成若干区域,每个区域内部像素之间具有相似性,同时不同区域之间具有较大的互异性。分割质量的好坏对后续的目标识别和解译等工作具有重要作用。
一般的图像分割方法,多是基于像素的,即根据像素本身的灰度、颜色、纹理等特征进行分割; 根据具体方法不同,又有基于阈值、基于边缘、基于聚类,以及基于图论等许多方法[4-5]。对于遥感图像,不可避免地容易受到各种噪声干扰。而基于像素的方法,除了计算量大、实时性差以外,抗噪性也较差。而基于分裂-合并的分割策略则能有效地克服这些问题。基于分裂-合并的分割算法是从初始分割出发,基于区域特征的相似度,迭代地合并相似的2个相邻区域,直到满足某个代价函数而停止合并。这里涉及到3个方面: ①初始分割,产生的过分割结果直接影响到最终分割结果的质量; ②区域特征提取,所提取特征是后续区域合并的依据; ③区域合并,包括区域的相似度独立和合并准则的确定。学者们从这3方面对合并-分裂算法进行了广泛而深入的研究[6-8]。
与一些传统方法(如分水岭算法)相比,超像素将图像中局部特征(如纹理、灰度和颜色等)相似作为一个视觉意义上的整体,替代大量原始像素来表达影像特征,更符合人类对图像的感知方式,减少了冗余信息,大大降低了计算的复杂度。因此,采用超像素方法进行初始分割成为主流[9-11]。Achanta等[12]提出简单线性迭代聚类(simple linear iterative clustering, SLIC)算法生成超像素。该算法利用颜色和空间特征,生成形状规则、尺寸均匀的超像素块,其算法简单,计算速度快,而且超像素块数目调节方便,是超像素分割的经典算法。
目前使用最广泛的遥感图像分割方法是eCognition软件中的分形网络演化算法(fractal net evolution approach, FNEA )。该方法是一种多尺度分割方法,通过计算和比较图像光谱和形状的相似性,自下而上的逐层合并对象。但该方法需要手动反复调节尺度、紧致度和异质度等多个参数,才可能得到较好的分割效果[13]。概率密度估计是概率统计和模式识别中基本问题之一,主要分为参数估计和非参数估计。密度估计在图像分割的应用也很广泛,最为著名的是基于非参数估计的均值漂移算法[14-15]; 此外非参数估计还应用于基于阈值的图像分割中[16]; 而基于参数估计的有限混合模型也经常用于图像分割的建模中[17-18]。
本文基于分裂-合并的分割策略,在对图像进行超像素初始分割的基础上,对每个超像素块进行非参数密度估计,并基于估计的密度,重新将超像素块合并聚类,提出一种新的遥感图像分割算法。
1 基于超像素及其最小生成树上Parzen窗密度估计的图像分割算法
本文方法的主要思路是: 先将图像进行初始超像素分割,把每个超像素块看作图上一个顶点,然后在图的最小生成树上测量顶点间的距离,采用Parzen窗估计方法,在图上估计每个顶点的概率密度,进而寻找不同密度函数的模态进行聚类。其基本原理示意图如图1所示。
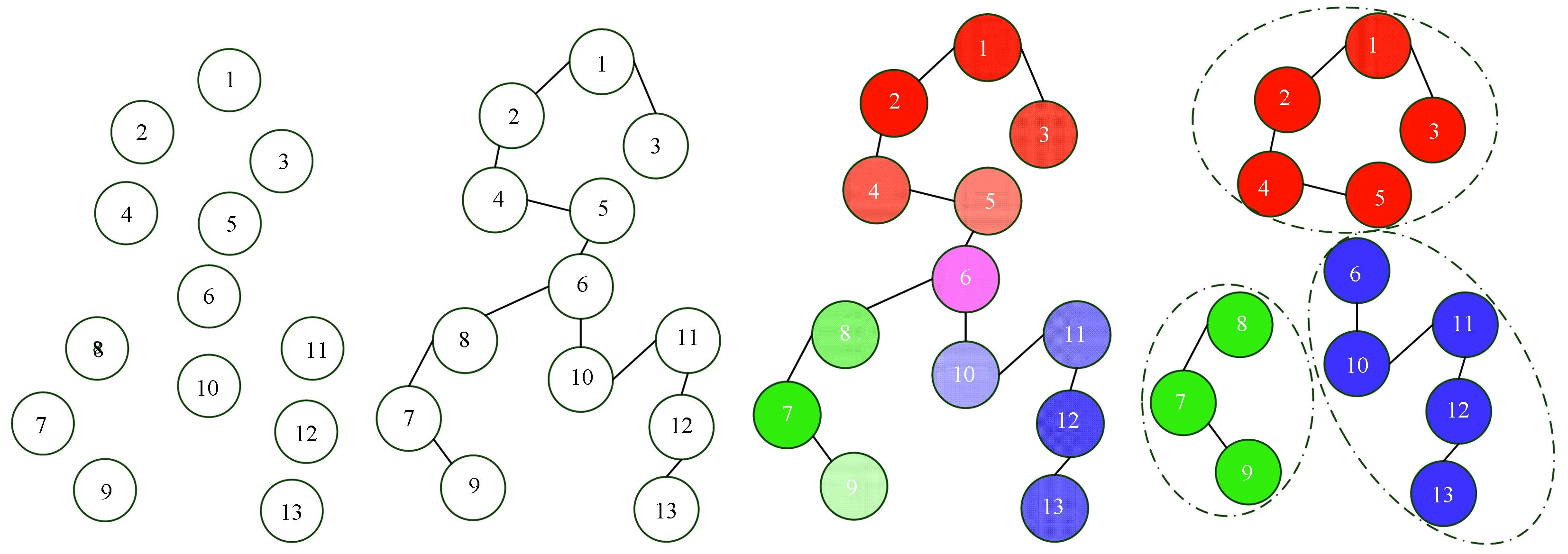
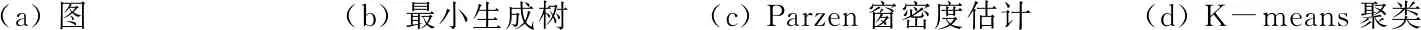
(a) 图(b) 最小生成树(c) Parzen窗密度估计(d) K-means聚类
以下先概述SLIC算法,然后给出超像素块的特征提取以及度量方法,再给出基于Parzen窗的密度估计方法,最后详细讨论提出的算法,并给出算法流程图。
1.1 SLIC算法
SLIC超像素分割算法的步骤为[12]:
1)初始化种子点。根据输入图像的像素点个数L,均匀地在图像中设置k个种子点,则超像素大小为L/k。
2)种子点处理。在种子点的3×3邻域内对所有像素进行搜索,将种子点移动到该邻域内梯度最小的位置,以避免种子点落在边缘位置,从而确定更好的聚类效果。
3)距离测量。将图像转化到Lab颜色空间,分别计算每一个像素点i与该种子点j的颜色距离和空间距离,公式分别为:
(1)
(2)
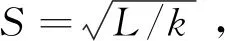
(3)
4)迭代聚合与连通性处理。重复上述步骤,直到聚类结果稳定,一般迭代十余次即可终止。但可能会存在一些孤立像素或是多连通像素,使用分量连通方法以产生紧致连通的超像素块。
1.2 区域特征的提取与度量
与传统傅里叶方法不同的是,Gabor滤波器可以同时在频率域和空间域都有较好的分辨力,可以方便地在方向和尺度2个参数上进行调整,以符合人类的视觉特性。Gabor滤波器的小波特性使其可以详尽地描述图像纹理特征[19]。
设m,n分别为尺度参数和方向参数的Gabor滤波器组表示为gmn(x,y), 给定图像I(x,y),将该图像与Gabor滤波器组的卷积得到该图像的Gabor变换Wmn(x,y),即
Wmn(x,y)=I(x,y)⊗gmn(x,y)。
(4)
对于滤波后的图像Wmn,可得其均值μmn和标准差σmn,则图像I(x,y)的纹理特征向量为[μ11,σ11,μ12,σ12,…,μmn,σmn],共计2mn维。实验中,取3个尺度(m=3),8个方向(n=8),因此纹理特征为48维向量。
1.3 Parzen窗密度估计
Parzen窗密度估计(Parzen windows density estimation)又称核密度窗估计,是一种重要的非参数密度估计方法,最早由Parzen[20]提出,它不需要向参数估计方法那样,假定数据分布的概率密度函数参数形式已知,它可以对任意分布的数据作密度估计。现有N个d维空间样本x1,x2,…,xN,Parzen窗密度估计即以这N个已知样本来对空间中任一点x的概率密度进行估计,即
(5)
式中: 参数h为核函数的带宽(bandwidth);K(·)为核函数(kernel function),一般为对称和单峰的函数,且满足如下条件,即
(6)
1.4 提出的算法
经过超像素初始分割后,2个超像素块直接的纹理相似度定义为:
(7)
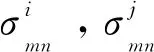
根据超像素块之间的纹理特征的相似度,每个顶点(超像素块)vi的概率密度由与它相连的顶点按照Parzen窗密度估计方法可以估计为:
(8)
式中G(·)为Gaussian核函数。在式(8)中仅仅包含了纹理信息,而没有考虑空间信息,而实际上邻接的超像素块极有可能属于同类,即具有近似的概率密度。因此,本文提出同时包含纹理信息、光谱信息和空间信息的Parzen窗密度估计方法。
最小生成树是最小权重生成树的简称,它是无向图中包含所有顶点且权值和最小的子图,任意2个顶点之间距离同时蕴含了特征的相似度(权值)和空间的信息[25]。因此,用最小生成树上距离带入Parzen窗密度估计方法中描述顶点(超像素块)的概率密度。
首先,可以用经典的算法,如Krusal算法、Prim算法[26],在以超像素块为顶点的区域邻接图上建立最小生成树; 然后在最小生成树上寻找任意2顶点vi和vj的路径{vi,vi+1,…,vj},其中vi和vi+1是路径中相邻的顶点,这样,顶点vi和vj的距离DMST为:
(9)
式中wp,p+1为最小生成树上连接相邻顶点vp和vp+1的权值。然后,将式(8)中的wij替换为DMST(i,j)进行Parzen窗估计,即
(10)
可以看到,在Parzen窗密度估计中的距离DMST(i,j)中,既含有SLIC算法的光谱信息,也融入了超像素块的纹理信息,同时在最小生成树上度量也自然引入了空间近邻信息。在Parzen窗密度估计中是以每个顶点为中心的窗函数(这里是Gaussian核函数)到待估计点的叠加。由Gaussian核函数的性质,对概率密度有所贡献的点只能是与待估计点空间距离较近(累计权重较小)的点,以及与待估计点特征(光谱特征、纹理特征)相似(边上权重较小)的点。所以,本文提出的这种概率密度估计方法是合理的。
对于万能轧机的重轨生产,轧机对型钢断面的轧制要高于普通轧面20 m左右。在离钢轨尾部10 m的范围内,会存在一个高于正常轨道0.5 mm以上的“高点”,该“高点”会在钢轨有0.5 m左右的持续长度。对于这些影响列车运行的“高点”,传统“高点”处理方式为器具打磨,但器具打磨会严重影响钢体的质量与寿命。而使用全轧程热力耦合数值模拟系统,能够完成E孔型和UF孔型的连轧工作。其中UF孔型属于半封闭的轨道孔型,轧件在离开E轧机进入UF轧机的过程中,会由于半封闭孔型而发生“甩尾”现象,轧件尾部会明显高于脱离轧机时的轨高。
最后,将具有相似的概率密度的顶点被认为属于同一模态(类),采用K-means算法完成聚类,得到最终分割结果。整个分割算法流程如图2所示。

图2 提出的多光谱遥感图像分割算法流程
2 实验结果及讨论
本文多光谱遥感图像分割的实验平台为2.8 GHz的Pentium4处理器、8 G RAM的计算机,采用软件为MATLAB R2004a。实验1是讨论参数的选择对提出算法分割效果的影响; 实验2和实验3是将提出的算法与eCognition软件中不同参数FNEA算法作对比,验证提出算法的有效性。
为了更有效地评价分割结果,从定性和定量2个方面进行评价。定性即为主观的目视对比判别; 定量则基于手动标注的实际地物边界采用P-R方法[27]计算,公式分别为:
Precesion=TP/(TP+FP),
(11)
Recall=TP/(TP+FN),
(12)
式中:Precesion为准确率,其值越大,表示分割精度越高;Recall为召回率,其值越大,则表示边界的附着度越好;TP为被正确分割的地物目标像素数目;FP为被误分为地物目标的背景像素数目;FN为被误分为背景的地物目标像素数目。
2.1 实验分析一
该实验遥感图像选自NWPU VHR-10数据集[28]。图像采集自Google Earth,包括10个类别目标的高分辨率RGB彩色图像和红外图像。实验图像为数据集中178号图像的局部,其中包括船只、水体、植被、建筑物、桥梁等地物目标,图像大小为266像素×385像素,如图3所示。该实验目的是讨论提出算法中的参数设置对分割效果的影响。在提出的算法中主要需要设置3个参数: ①SLIC算法中的S,用于控制超像素块大小; ②Parzen窗带宽h; ③K-means的聚类数。聚类数的选择无疑会对聚类效果有较大影响,许多文献讨论如何自动选择聚类数的问题[29-30],这不是本文主要关注点(实验中发现,只要聚类数在一个大致合理的范围内,分割结果相对稳定,限于篇幅,没有给出实验图像),实验中还是依据经验采用手动给定聚类数。该实验中,所有的聚类数手动选择为5。

图3 实验1的原始图像
表1中给出了参数S和h取不同数值时的分割结果。其中,从左至右,第1—3列依次是S设置为5,20和50时的分割结果; 从上到下,第1行为超像素预分割结果,第2—5行分别是带宽h取0.5,5,20和50时的分割结果。参数S越小,预分割的超像素

表1 实验1的分割结果
块数目就越多; 反之,S越大,超像素块越大,其数目就越少。因为采用的是分裂-合并的分割策略,若S设置过大,会使得后续合并的分割结果过于粗糙,容易产生欠分割问题(如表1第3列所示)。由于合并过程是基于Parzen窗密度估计,这也要求样本点不可以过少。由于样本点过少,导致密度估计不够准确,也是导致表1第3列中分割效果较差的原因之一。但另一方面,若S设置太小,超像素数目过大,会使得计算量(包括超像素分割、纹理特征测量和Parzen窗密度估计)显著增加。
表2中是参数S取不同值时的平均计算时间的比较,容易见到S取5时比取20时计算时间增加了近2倍,同时分割效果并不更好,且更容易出现过分割问题(见表1第1列与第2列的比较)。

表2 实验1中参数S的选取对计算时间的影响
另一个参数带宽h,涉及到密度估计的准确性,自然会影响到最后聚类结果(如表1第5行h=50时,带宽取得过大,严重降低了分割效果)。但同时,实际的分割结果对带宽的选择相对而言并不敏感,如第2—4行,带宽差异并不小,可分割结果却远没有预计的大。实际上,实验中选择了多个带宽,结果表明,只要带宽不是过大(如第5行)或过小,分割结果差异不会太大。而实验中采用文献[24]的方法都能够选择到理想的带宽。所以,后面的实验都是采用该方法自动选择带宽。
从表3的P-R定量评价中也可以看出,这2个参数的选择在Precision指标和Recall指标上基本也可以反映出于目视判别解读相同的结论。
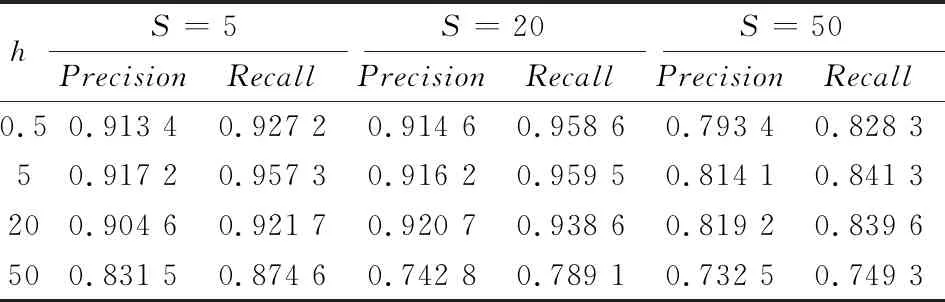
表3 实验1的定量评价
2.2 实验分析二
实验2图像是2010年4月15日青海玉树7.1级地震发生后由QuickBird卫星拍摄的多光谱图像,分辨率为0.6 m[31]。实验中采用了其局部图,大小为650像素×838像素,包含植被、建筑物、道路、山体等地物目标,如图4(a)所示。图4(b)和(c)分别是FNEA算法尺度参数分别设置为50和150的分割结果,其中形状异质度和紧致度参数分别设置为默认值shape=0.1和compactness=0.5。图4(d)—(f)都是本文方法的分割结果,其中带宽h由文献[24]的算法自动选择,类别数设置为6,图4(d)—(f)参数S分别设置为5,20和30。

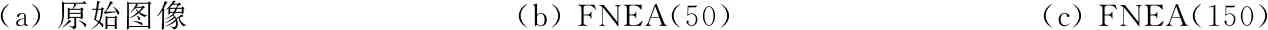
(a) 原始图像(b) FNEA(50)(c) FNEA(150)

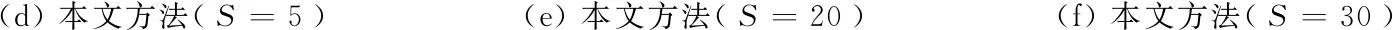
(d) 本文方法(S=5)(e) 本文方法(S=20)(f) 本文方法(S=30)
实验3图像是NWPU VHR-10数据集[28]中286号图像的局部图,图像大小为751像素×979像素,包括飞机、水体、舰船、植被、机场地物标志等地物目标,如图5(a)所示。与图4中实验2类似,图5(b)和(c)分别是FNEA算法尺度参数分别设置为150和200的分割结果,其中形状异质度和紧致度参数也都设置为默认值shape=0.1和compactness=0.5。而图5(d)—(f)也是参数S分别设置为5,20,30的分割结果,带宽h由文献[24]中算法自动选择,类别数设置为5。

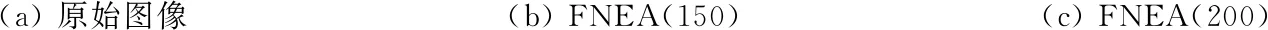
(a) 原始图像(b) FNEA(150)(c) FNEA(200)

(d) 本文方法(S=5)(e) 本文方法(S=20)(f) 本文方法(S=30)
从图4(b)和(c)以及图5(b)和(c)中可以看到,在FNEA方法中,当尺度参数变大,则过分割的问题会得到一定程度克服,但很难完全避免。如图4(b)和(c)中的植被部分,由于植被的光谱异质度较大,产生了明显的过分割,而图5(b)中的水体部分,由于光谱相似度较大,也产生了比较明显的误分割问题。而尺度参数大,又很容易产生欠分割,如图5(c)。同时,图4中建筑物的光谱信息“同谱异物”的情况比较明显,大多数尺度情况下,都容易出现过分割情况。所以,很难找到合理的尺度参数,同时避免以上各种问题的出现。从表4和表5中的定量评价来看,实验2和实验3中分别取比较典型的大小2个不同尺度参数FNEA方法分割结果,其大尺度下的Precision和Recall指标均较小尺度下的有所提高,但非常有限。这也从另一个方面印证了上面的分析。

表4 实验2定量评价

表5 实验3定量评价
在本文方法中,初始分割阶段,SLIC算法考虑了像素的光谱特征; 然后又融入了超像素块的纹理信息; 距离测量时,利用最小生成树结构,整合了超像素块的空间近邻信息。在此融合了各种信息的距离测度基础上,用Parzen窗估计顶点密度,距离较近的顶点(超像素块),其密度应该更接近,后续的K-means算法更倾向于将其分为一类。因而,从图4和图5的(d)—(f)中也可以看到,本文方法能够在一定程度上处理好过分割、欠分割和误分割等问题,即使地物目标复杂的遥感影像,也可以产生较为合理的分割结果。
但是,正如实验1中所指出的,提出的算法中超像素预分割中参数S还是对分割结果有一定影响,如图4和图5中(d)比(e)和(f)存在更明显的过分割问题。所以参数S取得过小,超像素块数目过多,合并的效果并不好; 当然,参数S过大也容易出现分割效果粗糙(实验2和3中没有再给出分割效果图)。好在分割结果对参数S并不十分敏感,只要位于合理范围(实验中一般在10~30之间),其分割结果相对比较接近(如图4和图5(e)和(f))。在表4和表5的定量分析中也可以看到,提出的算法中参数S取5,20和30时,Precision和Recall指标均比FNEA方法好,而参数S取20和30的结果则提高更明显,且比较接近。
3 结论
针对传统基于像素的遥感图像分割算法易受噪声干扰、计算效率低等缺点,在分裂-合并的框架下,本文提出了一种将超像素和Parzen窗密度估计相结合的遥感图像分割方法,该方法预分割阶段是采用SLIC算法将遥感图像粗分割为超像素,每个超像素块视作图结构中的一个顶点,在图的最小生成树上测量顶点间距离,并采用Parzen窗估计每个顶点密度,然后以这些概率密度为指标对超像素块进行K-means聚类,以达到“融合”目的,得到最终分割结果。提出的方法中有2个方面的主要工作: 一是构建了基于最小生成树的整合了光谱信息、纹理特征和空间信息的距离测量方式; 二是提出了基于图上顶点的Parzen窗密度估计的聚类方法。
为验证提出算法的有效性,在多种多光谱遥感图像上进行分割实验。通过算法中不同参数下的分割结果,以及与不同参数的FNEA算法的分割结果进行比较研究,可以发现提出的算法结果稳定,鲁棒性较好,同时能够克服过分割、误分割和欠分割等问题,得到较好的分割效果。
