海岸带地类统计模型中DEM空间尺度优选方法

江娜, 陈超, 韩海丰

(1.山东省国土测绘院，济南 250013； 2.浙江海洋大学海洋科学与技术学院，舟山 316022)

0 引言

海岸带是陆地和海洋之间相互作用的交汇地带，受人类活动影响大，其自然和生态环境极其脆弱和敏感[1-4]。随着自然资源及各项调查监测工作的开展，依据不同的分类体系，管理部门形成了多源、海量的地理数据，能够客观反映海岸带土地、森林、草原、湿地等要素空间分布情况。为准确评估海岸带“山水林田湖草”等自然资源情况以支撑海岸带保护开发与科学利用，需要以数字高程模型(digital elevation model，DEM)数据为三维空间基底，通过地类统计模型摸清地类表面面积底数，以揭示该特殊区域地类分布的空间特性、相互关系及其分布规律[5]。

DEM是地表形态的数字化表达，蕴含了三维分析所必需的地形地貌信息。多尺度是DEM的重要特征，数字地形应用分析面临各种尺度问题[6]。DEM空间尺度对自身信息量、数据精度[7-9]，以及坡度、坡向、曲率等地形因子具有直接的影响。此外，DEM尺度对地貌类型划分[10]、生态价值评估[11]、土壤有机碳制图[12]、土壤侵蚀预报[13]、水文模型构建[14-15]和岩性识别与分类[16]等均具有重要影响。随着DEM采样间隔增大，地形描述精度呈降低趋势[8]，地形信息被综合，地形概括能力增强，整体趋于平坦化[17]。在开展具体的应用与分析时，需综合考虑统计模型与DEM数据尺度匹配的问题[9]，选取适宜的研究区间。在海岸带地类统计模型构建过程中，DEM空间分辨率越高，越能真实、精准地表达区域地形地类空间分布，但数据体量和计算密度急速增加，影响计算和存储的效率[5]，还会导致局部区域出现微地貌，影响地类整体统计结果。因此，开展海岸带自然资源地类三维统计时，需综合考虑地类的空间结构、分布特点、采集指标、统计精度和计算效率等因素的影响选取最优尺度的DEM数据。

当前，鲜有针对于DEM尺度与自然资源地类统计适配性问题的专门研究，各调查监测成果统计中采用的DEM尺度也不一。在基于无缝场模型开展的大型自然资源调查监测中，地理国情监测数据基本统计主要基于10 m格网DEM开展； 第三次国土调查成果以各省最精细DEM生成的坡度数据(如山东省基于2 m格网DEM数据)，分级统计耕地等地类面积。针对于此，本文研究海岸带统计模型与DEM空间尺度的关系，讨论影响统计结果的主要因素，构建评价模型，提出了一种针对海岸带地类统计的DEM空间尺度优选方法。本文提出的方法为海岸带地理国情监测、第三次国土调查、森林资源调查以及其他调查监测的地类统计DEM尺度选取提供了理论和实践依据并可推广至其他区域。

1 研究方法

海岸带地类统计模型中DEM空间尺度影响结果的准确性、概括性、信息量和计算效率。在本方法中，以现有最高精度DEM为数据源派生出多尺度DEM数据，以精准的地类图斑数据为待统计数据源，从DEM空间尺度对统计结果的准确性、概括性、信息量和计算效率等4个方面选取影响因子构建评价模型，数学表达式为：

(1)

式中：S为总体影响评价；f(xi)为DEM空间尺度对准确性的影响；pxi为各准确性因子权重；y(yi)为DEM空间尺度对概括性的影响；pyj为各概括性因子权重；z(zk)为DEM空间尺度对信息量的影响；pzk为各信息量因子权重；o(og)为DEM空间尺度对计算效率的影响；pog为各计算效率因子权重。各DEM尺度影响因子层次结构如图1所示，其中*为限制性因子。

图1 DEM空间尺度评价模型

评价指标分为限制性指标和一般性指标，限制性指标对DEM空间尺度具有决定性： 当DEM空间尺度不满足限制性指标要求时，需剔除该尺度； 当满足需求时，与一般性指标共同参与影响力计算。基于客观赋权法-熵权法计算各影响因子权重，加权计算DEM各尺度综合得分，得分最高的尺度即为最优DEM空间尺度。具体技术流程如图2所示。

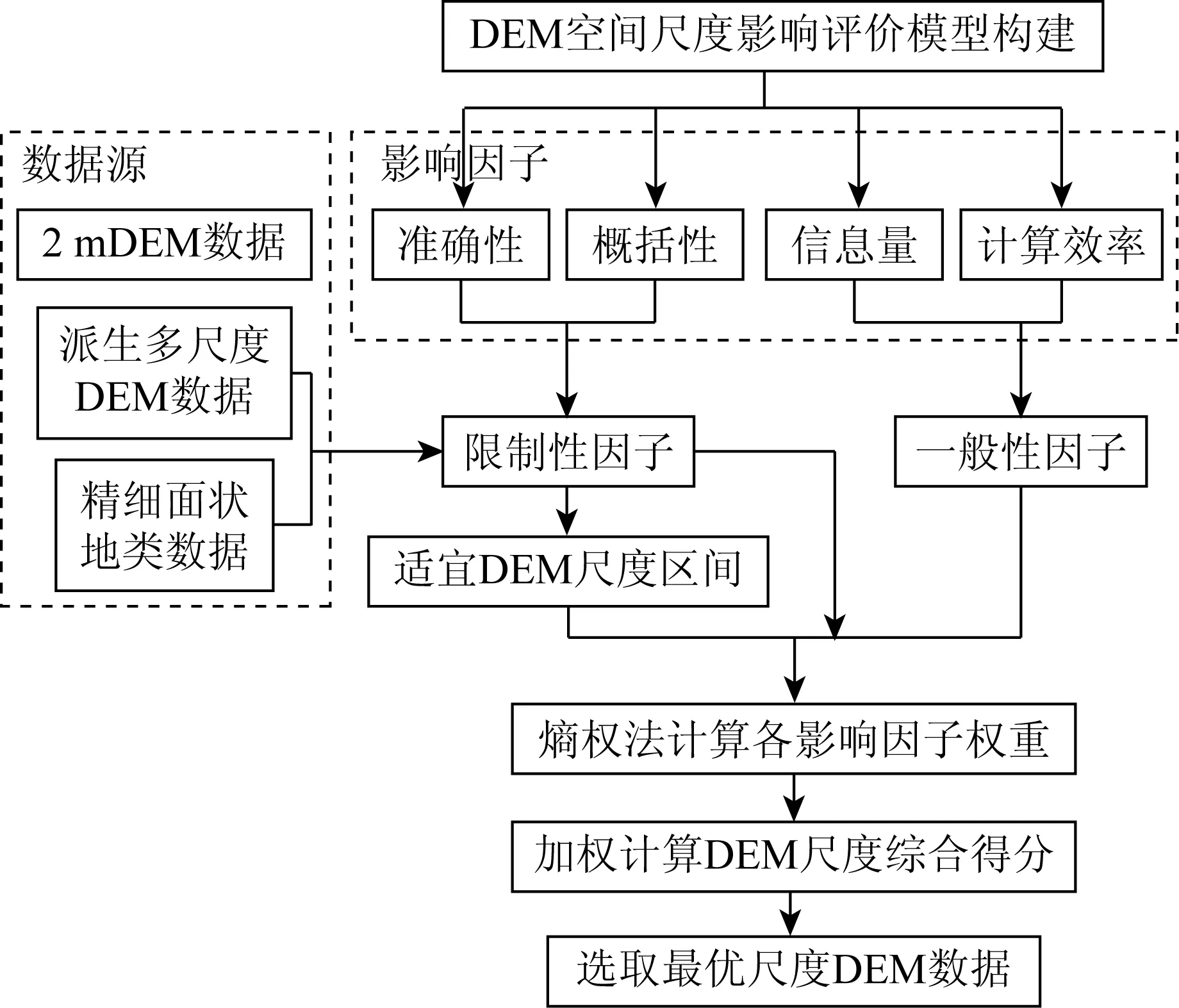
图2 技术流程

1.1 准确性评价因子

全国第三次国土调查、地理国情监测等自然资源调查监测成果属于“统一比例尺、统一分辨率、统一内容指标、统一采集标准的无缝隙、高分辨率、覆盖全域”的高精度地理要素数据[5]，对其开展统计分析需优先保证统计精度，即准确性。DEM空间尺度既要满足地类统计的精度要求，也需满足区域基本地形因子描述的精度要求，此处选取代表性地形统计因子： 高程最大值、最小值、地表平整系数[18]，统计各因子偏差率； 对于地类统计精度的测定，选取地类面积偏差率作为限制性指标。特别注意海岸带特殊地物(如独立房屋、固化池等面积占比小于0.1%的细小目标)的统计精度，以及铁路与道路等线状目标地类的统计偏差，将其作为限制性因子，当DEM尺度对特殊地物影响偏差超过设定阈值时，直接剔除该尺度。

准确性评价采用的指标为： 偏差率、偏差均方根。根据“DEM采样间隔增大，地形描述精度呈降低趋势[8]”这一基本规律，可将最高尺度DEM的地形统计和地类统计结果近似为真值。高程最大值偏差率mi计算公式为：

(2)

式中： max(hi)表示区域DEM尺度为im时DEM高程最大值； max(ho)为最高分辨率时的高程最大值，作为近似真值。地表平整系数是区域平面面积与地表表面面积的比值，反映地表的粗糙程度[18]； 最小值偏差率和地表平整系数偏差率计算公式与式(2)一致。

地类偏差率mi,j和偏差率均方根RMSEj计算公式分别为：

(3)

(4)

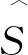
1.2 概括性评价因子

统计分析是从离散数据向信息、知识乃至智慧转化和提升的过程[21]，因此，统计结果要体现概括性和规律性。精细的DEM数据可能会保留局部微地貌，在地类统计过程中具体表现为坡度带破碎、数据量大，村台、路基等平坦地物存在较大坡度起伏。针对于此，选取微地貌概括因子来衡量DEM尺度的影响。

微地貌概括为限制性因子，反映DEM对于微地貌的综合情况。其计算方式为： 选取道路、平坦房屋建筑区等作为样本区(坡度带在0°～2°范围)，统计该范围0°～2°坡度带的面积占比Sp，公式为：

Sp=S0～2/S∑×100%，

(5)

式中：S0～2为样本区0°～2°坡度带面积；S∑为样本区总面积。借鉴中误差理论，统计值落入±2倍标准差范围内的概率为95.5%，因此以95.5%作为微地貌概括因子的阈值。

1.3 信息量评价因子

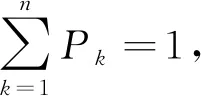
(6)

信息熵反映了数据不确定性的大小，数据信息熵越接近最大熵值,其分布也越规则[23]。在地类统计过程中，首先计算地形因子坡度带和高程带的信息熵； 其次以地类为单元，统计不同DEM尺度下地类信息熵； 最后，选取耕地、园地、林地、草地等空间分布与地形关联较大的地类计算坡度带信息熵。信息量评价因子为一般性因子。

1.4 计算效率评价因子

计算效率是评价统计模型经济性的重要因素，选取DEM格网数量以及相同处理环境下不同空间尺度DEM重要处理环节运行的时间等2个因素来开展计算效率评价，2个因子均为一般性因子。

1.5 熵权计算

通过限制性因子筛选适宜的DEM尺度，基于熵权法确定各因子权重。熵权法适用于定量指标的客观赋权和无量纲化[24]，其基本思想是认为评价指标的差异程度越大越重要，则权重相应也越大[25]。熵权法计算权重可分为以下步骤[25-27]：

1)构造原始指标数据矩阵Ru×v，即

(7)

式中：u为评价指标数量；v为评价对象数量。

2)对原始指标数据进行归一化处理，得到标准化矩阵I，即

I=(rij)u×v，

(8)

式中rij为第j个评价对象在第i个评价指标上的标准值，rij∈[0,1]。对于正向指标为：

(9)

式中： minRi和maxRi分别为第i个评价指标的最大和最小值。对于负向指标为：

(10)

3)定义熵。在式(6)的基础上，第i个指标的熵Hi定义为：

Hi=H(Ci)/lbv。

(11)

4)定义熵权。第i个指标的熵权wi定义为：

(12)

2 实验与分析

2.1 研究区概况

本次研究以山东省海岸带区域为研究区(图3)，包括山东省沿海34个县级行政区划，涉及7个地市，位于N35°04′～38°24′，E117°30′～122°42′之间，陆域面积为4.14万km2。山东省滨州、东营、潍坊等沿海区域濒临渤海，为黄河三角洲冲积平原地区，地势平坦； 东部烟台、青岛、威海、日照沿海为胶东丘陵地貌。海岸带地表覆盖和土地利用方式丰富，以耕地、草地、园林地为主，建设用地占区域面积的21.4%； 同时，海岸带是水陆交接、人类活动频繁的区域，其生态保护和开发具有重要的意义，以此为研究区具有典型性和代表性。

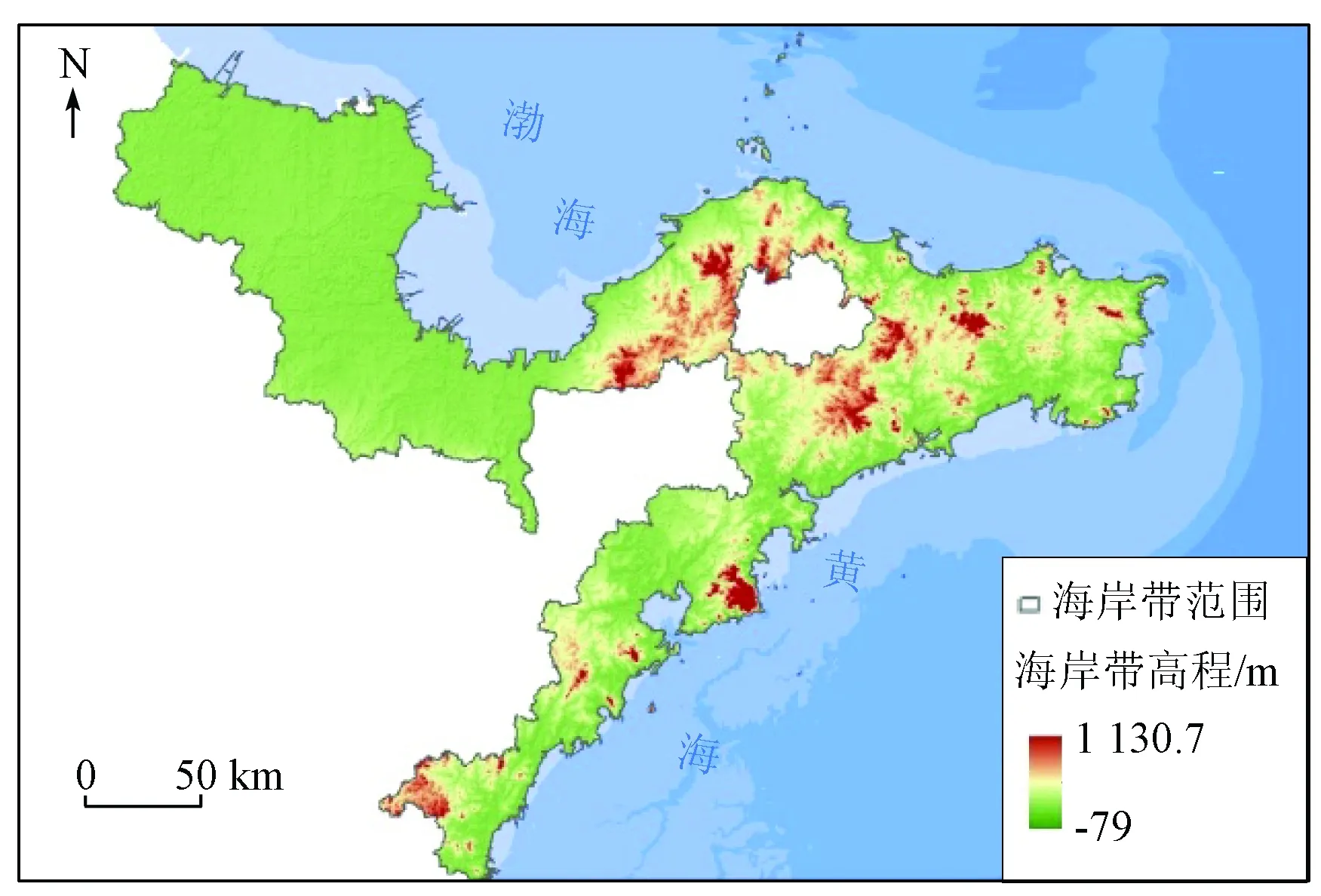
图3 研究区地形

2.2 数据来源

以2020年地理国情监测地表覆盖面数据为地类数据源，分为耕地、园地、林地、草地、房屋建筑(区)、铁路与道路、构筑物、人工堆掘地、荒漠与裸露地表、水域等10个一级类，分类标准参见《GDPJ 01—2013地理国情普查内容与指标》。DEM数据基于LiDAR点云数据生产，空间尺度为2 m，数据现势性为2014—2019年，是迄今为止山东省精度最高的DEM数据。以2 m格网DEM数据为基础，在ArcGIS软件中采用空间重采样方式，派生5 m，10 m，15 m，20 m，30 m，40 m，50 m，60 m，70 m，80 m，90 m，100 m等12个不同尺度的DEM数据，参与计算的DEM共计13个尺度。部分尺度DEM数据如图4所示。

(a) 2 m(b) 5 m(c) 10 m

(d) 20 m(e) 30 m(f) 50 m

2.3 结果与分析

2.3.1 准确性分析

基于2 m格网DEM统计区域地形特征，山东省海岸带高程值在[-79.0，1 130.7]m之间，均值为49.6 m，地表平整系数为0.977 6。随着DEM空间尺度增大，区域地表平整系数不断增加，越来越趋近于1； 最大值被综合，呈逐渐减少的趋势，最小值和均值局部存在较大波动，见表1； 偏离率呈现增加的趋势，如图5所示。

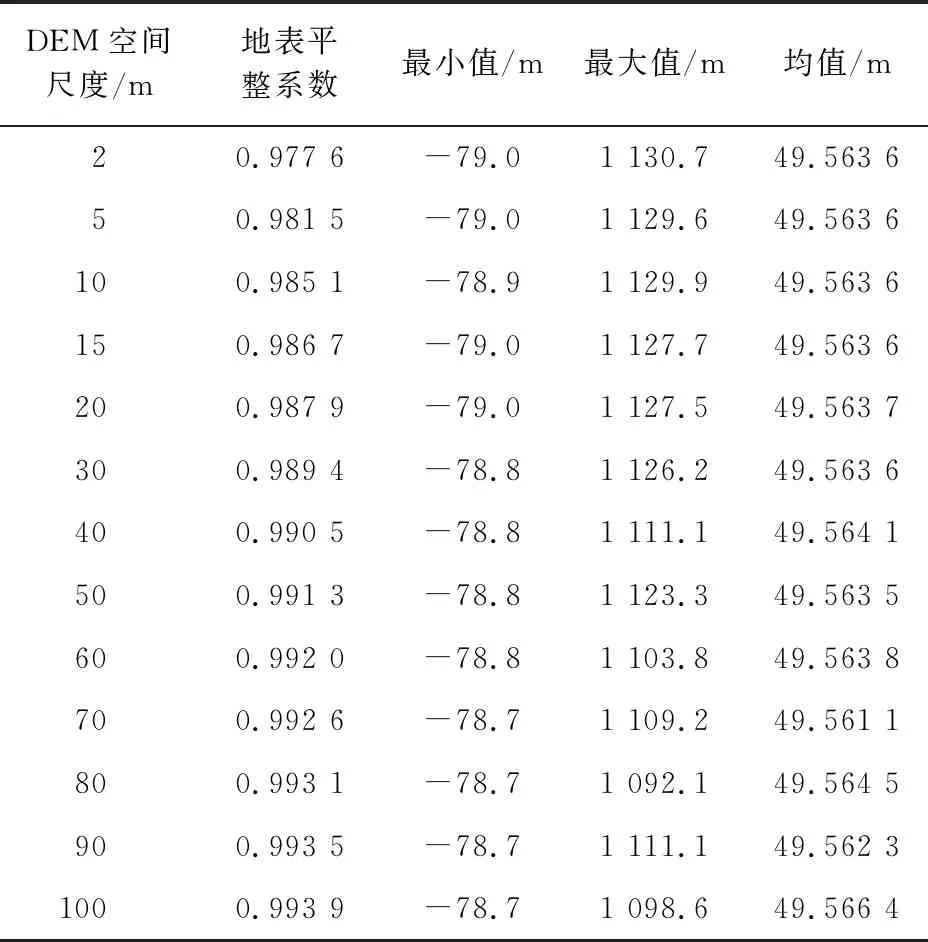
表1 地形统计特征与DEM空间尺度的关系

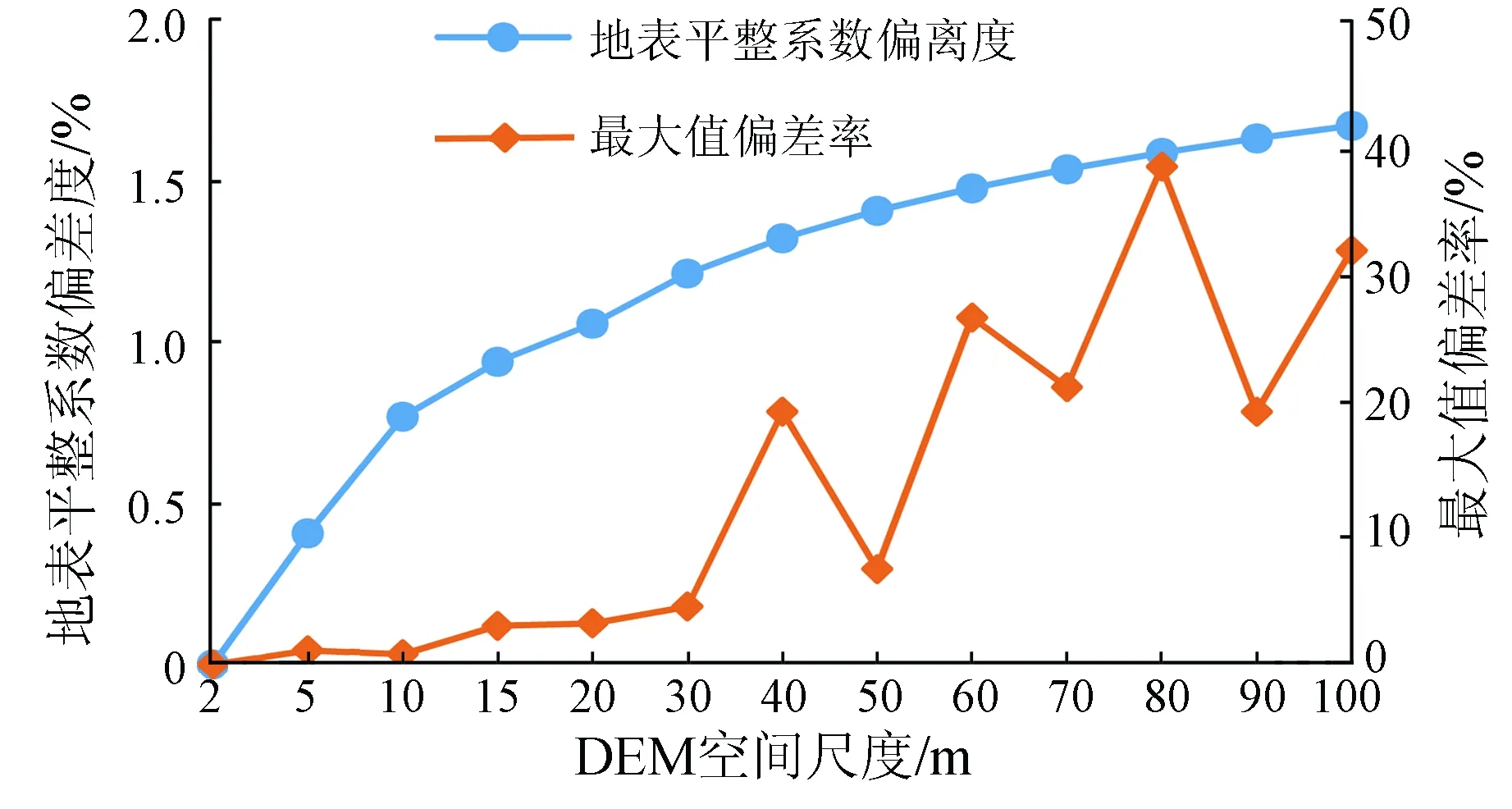
图5 地表平整系数和最大值偏差率随DEM空间尺度变化

极值点的限差依据CH/T 9009.2—2010相关规定确定，2 m格网DEM近似于1∶5 000比例尺DEM精度要求，高程最大值位于崂山山区，按山地推定高程中误差为2.5 m，最小值均位于莱州市平原地区，推定高程中误差为0.5 m[19]。以2 m DEM作为真值，区域高程极值应在2倍中误差范围内，即最小值、最大值分别需在(-79.0±1.0) m、(1 130.7±5.0)m范围内。对比重采样后高程极值，按最大值推定合适的尺度区间为[2,30]m，按最小值推定为[2,100]m，根据地形精度要求DEM空间尺度需在[2,30]m之间。

除地形特征外，还需保持地类统计结果的准确性，特别是对线状以及小目标地物的统计精度。计算结果发现，随着DEM尺度的增加，地类统计精度整体呈现降低的趋势，如表2所示。文献[20]中提及统计精度在万分之几的量级上可满足需求，因此选取地类偏差率阈值为10/10 000，得到DEM空间分辨率需小于等于30 m。面积较小、细长地物的地类统计对于DEM尺度要求更高，试验区内线状地物以铁路与道路为例(图6)，小目标地物以区域面积最小的2个子类草本果园(19 596.4 m2)和露天稀土矿采掘场(24 752.6 m2)为例开展分析。对特殊地物放宽限差要求，按照主体在2倍中误差、置信水平95.5%内，发现铁路与道路因基数较大各尺度均可满足精度需求； 但小目标地物适宜DEM尺度分别限定在[2,50]m和[2,30]m之间(图7)。由此可见，地类统计和地形精度限制性因子对DEM尺度要求是一致的，即不可超过30 m。

表2 DEM空间尺度与地类统计精度关系

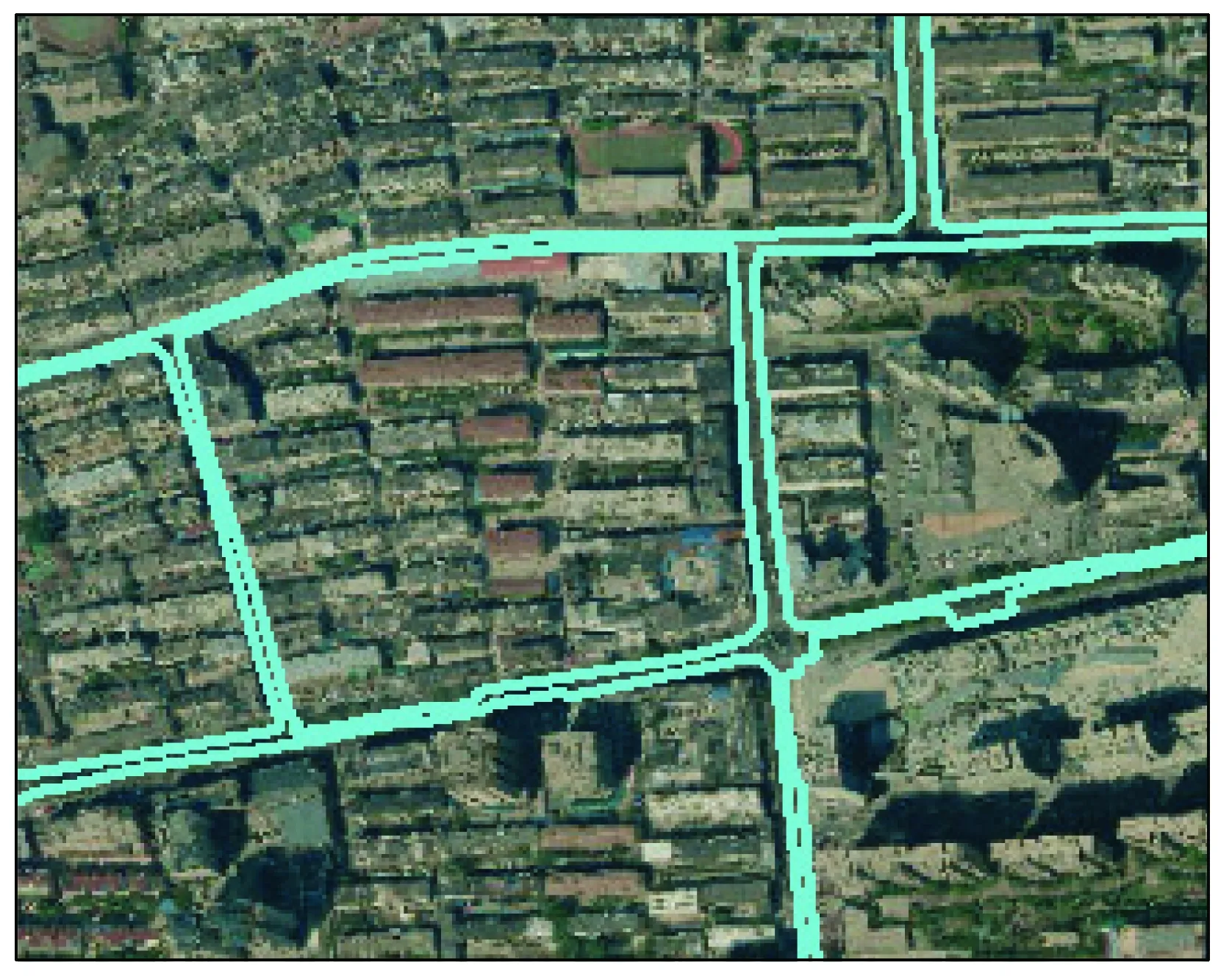
图6 线状地物示例

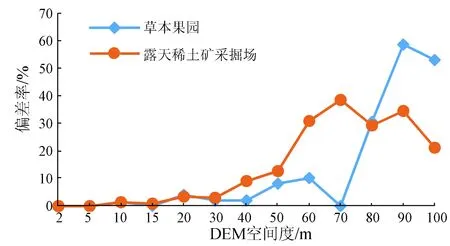
图7 小目标地物统计偏差率与DEM尺度的关系

2.3.2 概括性分析

结合遥感影像和DEM数据选取海岸带平坦地区(坡度≤2°)面积大于150 000 m2的低矮房屋建筑区为样本区，为避免房屋边界出现坡度突变，将边缘向内收缩5 m、去除多部件并再次筛选面积大于150 000 m2的376个样本区作为研究区。开展不同DEM空间尺度下房屋建筑区各坡度带分布统计，结果如表3所示。当空间尺度为2 m时，目标区2°以下坡度带面积仅占77.15%，5 m时占比为87.42%； 存在大量微地貌不利于地形统计，10 m及更大尺度时2°以下坡度带占比超过95.5%，满足地类统计的概括性限制要求。从概括性的角度来看，适当的DEM尺度综合对于去除微地形非常重要，在本试验中DEM格网尺寸不能小于10 m。

表3 房屋建筑区在不同DEM尺度下各坡度带分布情况统计

2.3.3 信息量分析

对不同尺度DEM数据开展高程带、坡度带分级，参照地理国情基本统计规程[18]及其操作实践，将研究区高程分为(-50,50)m,[50,100)m,[100,200)m,[200,500)m,[500,800)m,[800,1 000)m,[1 000,1 200)m等7个高程带，依据水土保持通用分类分级标准，将坡度分为(0,3]°,(3,5]°,(5,10]°,(10,15]°,(15,20]°,(20,25]°,(25,30]°,(30,35]°,(35,40]°, (40,45]°,(45,50]°,(50,55]°,(55,90]°等13个坡度带。计算结果发现，DEM空间尺度与坡度带信息熵呈负线性相关关系，即

y=-0.088 5x+2.376 1。

(13)

判定系数R2为0.933 1，坡度带信息熵随DEM空间尺度增加逐渐递减，从2 m到100 m，熵值丢失率(熵值减少值与初始值的比值百分比)为45.77%； 而高程带信息熵对DEM尺度不敏感，信息熵在[1.379 8,1.379 9]之间，变化量微小，与DEM尺度无明显相关性，如图8所示。

统计耕地、园地、林地和草地等植被的地类坡度信息熵，发现随着DEM格网增大，各地类信息熵均呈现降低的趋势，信息熵丢失率逐渐增大，变化情况如图9所示。

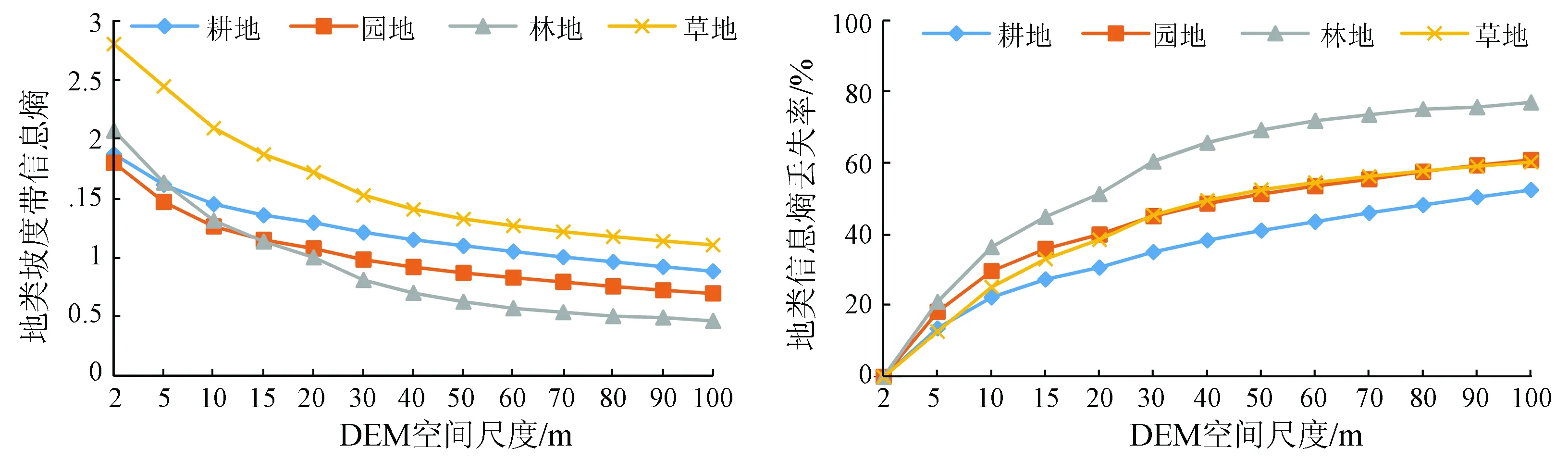
(a) 坡度带信息熵(b) 信息熵丢失率

当DEM空间尺度相同时，草地信息熵最大，2 m时值为2.80，而园地最小仅为1.80，表明草地在各坡度带的分布较其他地类相对均匀，而园地在坡度带上分布相对集中。同时，随着DEM格网增大，各地类在特定坡度带上的分布趋于聚集。100 m格网相对2 m格网地类的信息熵丢失率在[52.45%,77.07%]之间，林地的信息熵丢失率最大，表明林地坡度带信息熵对于尺度变化最为敏感。因耕地、园地、林地和草地等植被的地类坡度信息熵具有高相关性，在构建评价指标体系时，仅选取对尺度敏感度最高的林地坡度信息熵参与权值计算。

2.3.4 计算效率分析

考虑计算效率，山东省海岸带2 m空间尺度DEM共有103.4亿个格网，而100 m有413.7万个格网，格网数量与DEM尺度呈二次幂函数关系，即

y=4×1010x2。

(14)

从计算效率来看，以DEM坡度计算为例，2～100 m坡度带计算耗时分别为2 648.0，413.0，103.0，47.15，25.86，10.97，7.0，4.15，3.31，2.4，2.01，1.73和1.52 s，坡度计算时间与DEM格网数量线性相关，即

y=3×10-7x。

(15)

判定系数R2=1，如图10所示。由于要素数据量和计算时间高度线性相关，构建评价模型时，仅选取DEM格网数量作为一般性指标。

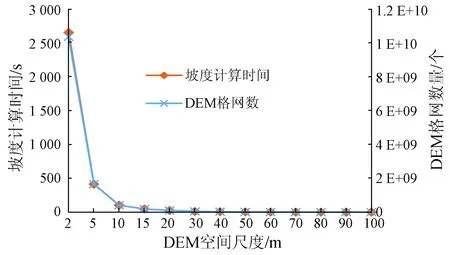
图10 格网数量、计算时间与DEM尺度关系

2.3.5 最优DEM尺度选取

通过限制性因子筛选，适宜海岸带地类统计的DEM尺度在[10,30]m之间，具体为10 m，15 m，20 m和30 m等4个尺度。按图1所示构建指标评价模型，对于高相关性的指标仅选取其中具有代表性的因子，构建DEM空间尺度对地类统计影响12×4阶指标矩阵R； 根据指标对统计结果影响的指向，区分为正向指标和负向指标，分别开展归一化，得到标准化矩阵I，计算熵值和熵权值，结果如表4所示。从一级指标来看，准确性指标熵权最大，为0.376 5； 计算效率熵权最小，为0.157 1； 信息量熵权为0.267 6，概括性熵权为0.198 8。从单项指标来看，微地形概括熵权值最高，为0.198 8，最小值偏差权重最小，为0.043 0，说明不同空间尺度DEM的微地形概括熵值差异最大，而最小值偏差统计熵值差异最小。将熵权值带入标准化后的指标矩阵I，按式(1)计算，10 m，15 m，20 m和30 m DEM综合得分分别为0.764 8,0.572 0,0.383 0和0.141 6，可以看出，随DEM采样间隔的增加得分呈降低趋势，准确性和信息量在海岸带地类统计过程中占主导因素。10 m格网是地理国情监测、第三次国土调查等海岸带地类统计分析的最优DEM空间尺度。

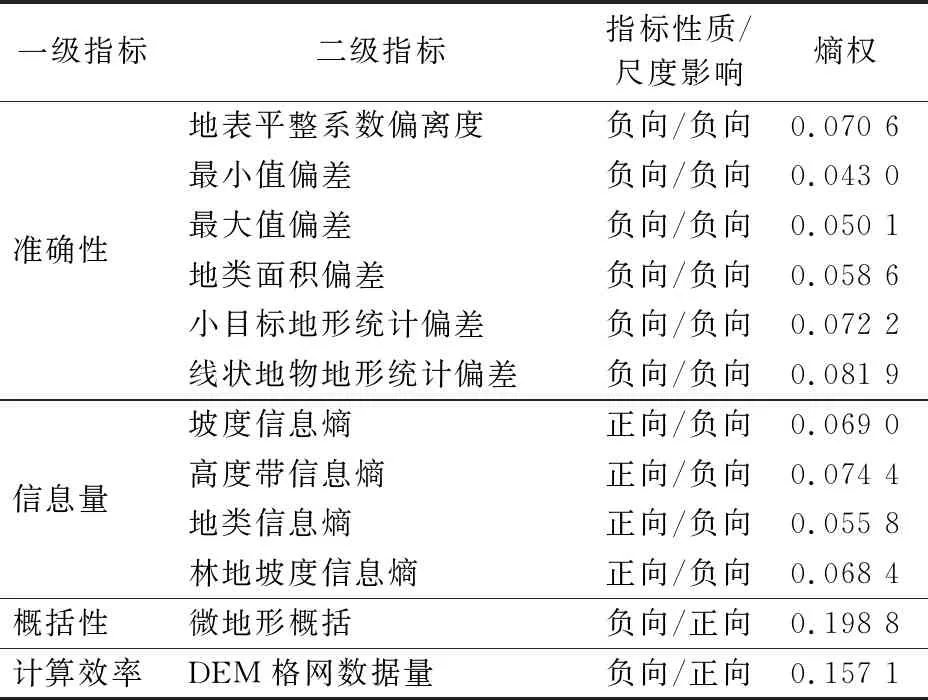
表4 熵权法确定指标权重

3 结论

本文首次系统探讨了海岸带DEM空间尺度对地类统计模型的影响，在准确性、信息量、计算效率等影响因子外，兼顾统计特性加入概括性影响因子共同构建评价模型； 将影响因子分为限制性因子和一般性因子，通过限制性因素筛选适宜的DEM空间尺度区间，在此基础上以熵权法客观赋权后加权统计各尺度DEM综合得分从而得到最优DEM空间尺度。主要研究结论如下：

1)不同影响因子对DEM精细度要求不一致，DEM格网越大，对统计准确性和信息量的负向影响越明显，对概括性和计算效率的正向影响越显著。

2)准确性因子对DEM精细度要求高，为满足统计准确性要求，空间尺度不应超过30 m，而地貌概括则要求空间尺度不能低于10 m。

3)空间操作计算时间与DEM格网数量线性正相关，而格网数量是空间尺度的二次幂函数。

4)基于熵权法计算权重后综合评价最优DEM空间尺度为10 m，综合来看，DEM准确度和信息量对尺度选取结果起到决定性作用。

本文形成的DEM空间尺度优选方法在海岸带自然资源及其他调查监测地类统计中具有通用性，也可扩展至其他区域，但需针对不同数据源、不同调查监测方式、不同使用目的等对指标和阈值进行适当调整。本文使用的DEM数据是以LiDAR点云为原始数据生成，对于细节表达较为精细，而采用其他方式生成的DEM数据在具体的计算结果上可能存在差异； 此外，本文以地理国情监测成果为地类统计数据源，其空间精度基本等同于1∶10 000比例尺基础地理信息数据精度，若考虑其他精度地类统计，同样可以采用本文提及的方法，针对具体的要求开展DEM尺度选取。