海洋能驱动航行器的能源最优航迹规划研究

李 可，宋志斌，刘骁锋，翟子正，李相杰，徐培鸿

（哈尔滨工程大学水下机器人技术重点实验室，哈尔滨 150001）

1 引言

近年来，随着无人水面航行器技术不断向自主化、智能化、大范围、长续航的方向发展，常规无人水面航行器由于自身能源不足，续航力有限的问题日益凸显，而海洋中蕴含着大量的能源，包括海洋自身的潮汐能、波浪能、温差能和盐差能等，还包括海洋上空的风能、太阳能以及海水中的生物质能。如何利用海洋中的能源来增加无人水面航行器的续航力已经成为无人水面航行器研究中的热点问题。

目前，无人水面航行器对海洋能源的利用方式主要有两种：一种是通过安装驱动装置，如波浪翼板、风帆等，将海洋清洁能源直接作为推力使用；另一种是通过安装海洋能源捕获设备，如风力发电机、太阳能电池板，将海洋中的海洋能源转换为其他形式的能源并储存起来，待需要时再提供给动力系统，这两种无人水面航行器可以统称为海洋能驱动航行器。

海洋能驱动航行器在执行任务时选择的航行路径直接影响着其能源消耗量和海洋能捕获量，路径的优劣也直接决定了海洋能驱动航行器续航力的高低。

2011年，庄佳园等[1]为解决无人水面航行器全局航迹规划问题，提出一种基于电子海图的距离寻优Dijkstra 算法。该算法使用动态网格模型，克服了传统Dijkstra 算法占用内存大的问题，可以减少规划时间，提高规划精度。2016年，Niu等[2]为了提高无人水面航行器的续航能力，开发了一种全局节能航迹规划算法。该算法集成了Voronoi 图、可见性算法和Dijkstra 搜索算法，并且考虑了海流数据，通过仿真试验分析了无人水面航行器在不同任务场景下的节能效果。2019年，贾知浩[3]为解决无人水面航行器在海流影响下的续航问题，提出一种考虑海流影响的节能航迹规划算法C-A*(A* Algorithm Considering Current Consumption，C-A*)。2019年，姚鹏等[4]为解决海洋环境下水下机器人的路径规划问题，提出一种基于最小一致性的路径规划算法。该算法能够有效减少水下机器人的能源消耗并提高路径平滑度。2019年，为解决人工势场路径规划问题中的局部最小值和目标不可到达问题，成昌巍等[5]提出一种基于动态窗口法的改进策略，改进后的人工势场法能够有效地使机器人逃离局部极小点并到达目标点。2020年，为解决无人机路径规划算法无法兼顾路径质量和计算效率的问题，王延祥等[6]提出一种基于扰动流场和深度神经网络的无人机自适应路径规划算法，该算法在保证路径质量的同时，有效减少了计算开销。

上述算法均为经典的无人航行器航迹规划算法。近年来，PSO 算法和GA 算法等仿生智能算法也被广泛地应用于无人航行器的航迹规划[7-9]。2018年6月，冯辉等[10]为达到在实际水流环境中减小无人水面航行器的能耗和保证无人水面航行器安全的目标，提出一种自适应混合粒子群（AHPSO）算法用于无人水面航行器的全局航迹规划。该方法根据海流中无人水面航行器航迹能耗等因素，建立多目标优化方程。针对粒子群算法早熟收敛等问题，采用自适应原理改变惯性权重和加速系数，有效提高了算法的寻优速度和精度。

可以看出，全局路径规划研究取得了较多进展，并且其逐渐由以路径最短为标准转变成以能耗最小为标准，由恒定不变的海洋因素条件转变为随时空变化的海洋因素。海洋能驱动航行器的能源最优航迹规划应当考虑的问题包含以下内容。

（1）对海洋能的捕获问题。伴随无人水面航行器技术研究的深入，为提高续航力，部分无人水面航行器逐渐由常规动力向海洋能驱动转变。目前的全局路径规划问题研究重点放在控制和规划层面，这就意味着很有必要考虑海洋能能量捕获问题。

（2）阻力导致的航行能耗问题。当下，大部分全局路径规划方法都把路径最短视为标准，较少涉及能耗问题，这就引起无人水面航行器路径搜寻时不可避免地加大能量消耗，特别是海洋能驱动航行器将会损耗更多的能量在航行过程中，而这直接关联到其续航能力。

本文基于A*算法，研究海洋能驱动航行器的能源最优航迹规划问题，通过分析海洋能驱动航行器航行过程中能源消耗的主要因素，建立海流能源消耗模型；通过分析海洋能驱动航行器航行过程中能够利用的海洋资源，建立风能捕获模型；改进A*算法，力求保证海洋能驱动航行器在到达目标点的同时，尽量少地消耗能源，尽量多地捕获海洋能源，提高海洋能驱动航行器的续航能力。

2 A*算法原理和地图模型的建立

A*算法的实现需要首先建立栅格地图模型。本文选取我国南海部分地区的实际海域作为研究对象构建地图，采用栅格法构建栅格地图模型，如图1所示。

图1 栅格地图模型Fig.1 Grid map model

为了使仿真试验的对比效果更显著，将海流的流向设置为以地图中线做分割，左侧流向90°方向（正北方向），右侧流向–90°方向（正南方向）；将风场的流向设置为以地图中线做分割，上侧流向180°方向（正西方向），下侧流向0°方向（正东方向）。风速设置为14 m/s。

栅格地图的尺寸为100×100（相邻网格之间单位距离取为1 km），透明方格表示无人水面航行器可以航行的海域，黑色方格表示陆地、岛屿或者其他障碍物范围。起点位置为(4,4)，终点节点位置(96,20)，相邻网格之间单位距离取为1 km。

A*算法是一种经典的路径规划方法，它主要结合了Dijkstra 搜索算法[11]与BFS 算法[12]的优点，回避了Dijkstra 搜索算法扩展节点过多、运行速度过慢和BFS 算法无法得到最优路径的缺点，能够在较短的运行时间内得到最优的路径[13]。A*算法主要引入了寻优函数、消耗函数和启发函数，可以根据用户的需要对寻优函数、消耗函数、启发函数进行调整，从而得到不同的目标路径。

不同的A*算法有着不同的寻优函数、消耗函数和启发函数。本文引入曼哈顿距离与对角线距离研究A*算法的寻优函数。曼哈顿距离[14]即直线距离，在本文中是指从当前节点移到目标节点的水平距离和竖直距离之和。

对角线距离[15]是指在曼哈顿距离的基础上，将对角线节点加入了A*算法的节点集合，即海洋能驱动航行器除了沿水平和竖直方向运动外，也可以沿东北、西北、东南、西南方向运动，基于对角线距离设计的寻优函数：

式中，c表示从一个节点移动到某一个相邻节点的消耗，可以是距离消耗，也可以是能源消耗等；Diagonal(p1,p2)表示从节点p1移动到节点p2的对角线距离，具体计算方法为：

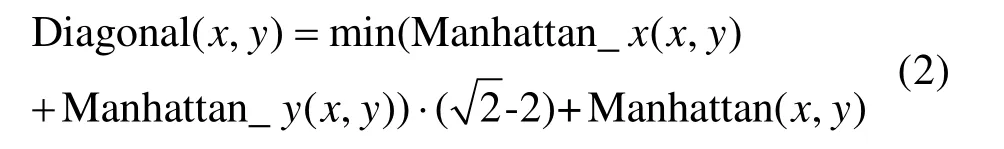
式中，Manhattan_x(,x y)表示节点x到节点y之间沿X轴方向的曼哈顿距离，Manhattan_y(x,y)表示节点x到节点y之间沿Y轴方向的曼哈顿距离。对角线距离的引入，使A*算法在进行路径规划时可沿对角线的方向进行搜索。

3 能源消耗模型和捕获模型构建

本文选取某型号海洋能驱动航行器作为研究平台，如图2所示。本章的研究内容集中于海洋能驱动航行器能源消耗模型和能源捕获模型的建立。考虑海流对海洋能驱动航行器航行过程中能源消耗的影响，建立海洋能驱动航行器在海流影响下的能源消耗模型[16-17]，如式(4)所示；在海洋能驱动航行器的海洋能源利用方面，考虑风的影响，建立风能捕获模型，如式(6)所示。

图2 海洋能驱动航行器Fig.2 Oceanic energy-driven vehicle

在网格地图的航行过程中，假设海洋能驱动航行器从节点n移动到节点n’，海流相对于大地的速度矢量用vc2e表示，海洋能驱动航行器相对于大地的速度矢量用vu2e表示，海洋能驱动航行器相对于海流的速度矢量用vu2c表示，三者的速度矢量用下式表示：

根据计算流体力学的相关原理和公式[18]，海洋能驱动航行器的能源消耗量E可以通过下式计算：

当已知海洋能驱动航行器的航行路径，海洋能驱动航行器与海流之间的相对速度vu2c和海流流速vc2e时，可根据式(3)和式(4)计算出该路径的能量消耗量。

考虑海洋能驱动航行器在航行过程中捕获的海洋能问题，本文建立风能捕获模型，其中，vw2e表示风相对地球的速度矢量，海洋能驱动航行器相对于风的速度矢量用vu2w表示，二者的速度矢量用下式表示：

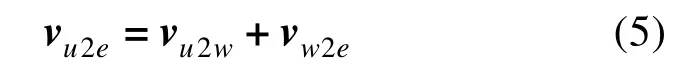
计算风的能量需要用到风能密度公式[19]：

式中，E2表示为风能密度；S表示风所流经的横截面面积，一般表示风力发电机风轮所掠过的面积；vu2w表示海洋能驱动航行器相对于风的速度；ρ表示空气密度；t表示风流经海洋能驱动航行器上风力发电机风轮的时间。

当已知海洋能驱动航行器的航行路径，海洋能驱动航行器与地球之间的相对速度vu2e和风速vw2e时，可根据上述公式计算出该路径的风能捕获量。

4 改进A*算法能源最优航迹规划

基于第3 节介绍的海流消耗模型和风能捕获模型，改进A*算法，设计考虑海流消耗和海洋能捕获的能源最优A*算法(N-A*)，N-A*的寻优函数表示为Estar_fun 2。海洋能驱动航行器航行过程中产生的能源消耗：

式中：Estar_cost 2(pstart,pcur)表示海洋能驱动航行器从起点航行到当前节点的过程中，海流引起的能源消耗减去风能的捕获量后的总的能源消耗值；Estar_heuristic2(pcur,paim)表示海洋能驱动航行器从当前节点航行到目标点中，海流引起的能源消耗减去捕获的风能后的总的启发值；μ和ν分别为它们的调节参数，其中μ≥0，ν≥0，μ+ν=1。

本文引入速度堆（以下简写为U_stack 和U_stack2）的概念，U_stack 为海洋能驱动航行器相对大地的速度堆，U_stack2 为海洋能驱动航行器相对风的速度堆，其结构均如图3所示。

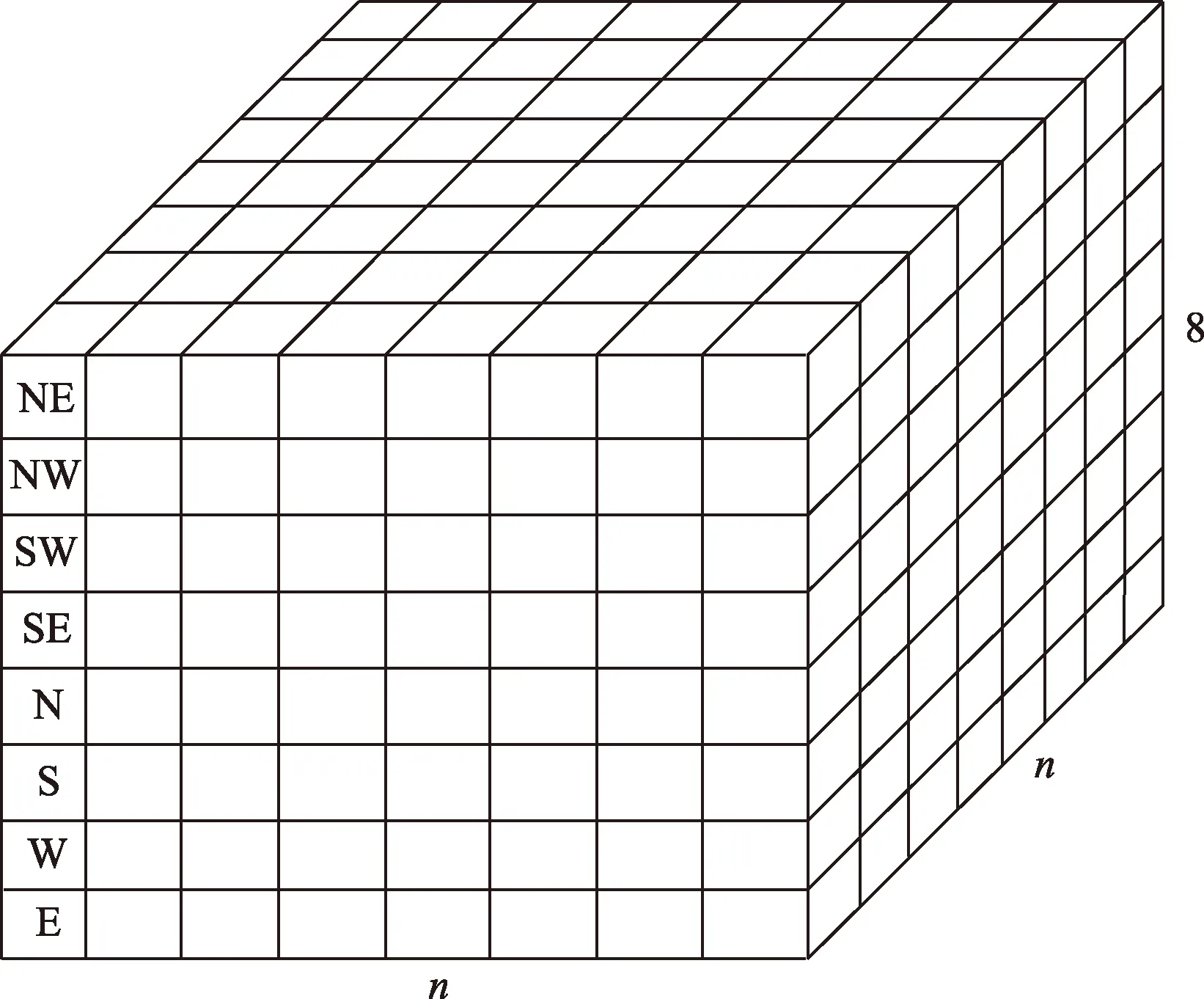
图3 海洋能驱动航行器速度堆Fig.3 Unmanned surface vehicle speed stack

以U_stack 为例，从最上层到最下层依次代表在n×n的网格地图上的每个节点海洋能驱动航行器在海流作用下向东北、西北、西南、东南、北、南、西和东8 个方向行驶时相对于大地的速度，以此实现全局地图中海洋能驱动航行器不同时速下对能量消耗的估算。

根据上文所述U_stack、U_stack2 对网格中各个节点的可能出现的运动方向设计能源消耗函数，依次对海洋能驱动航行器当前所在节点周围的8 个节点，其中i∊[1,8]，进行访问，并在U_stack、U_stack2 中选择对应行、列和层的，利用以下公式分别计算8 个节点的能源消耗，取其中的最小值作为下一步的能量消耗，其中变量d用来表示网格中两个相邻节点之间的单步代价，变量floor则表示或所在的层数。

为了使启发函数计算的能源消耗量尽可能地接近从当前节点到目标点的实际能源消耗量，启发函数需要计算启发路径长度：Lheu=Dheu+Sheu和任一节点(xi,yi)与目标点(xgoal,ygoal)之间的相对位置角度Arp。

Dheu和Sheu分别表示从当前节点pcur(x,y)周围的8 个节点(xi,yi)（其中i∊[1,8]）到目标点(xgoal,ygoal)的斜线的距离和直线的距离，计算公式(10)如下：

计算任一节点(xi,yi)与目标点(xgoal,ygoal)之间的相对位置角度Arp，并根据Arp的范围来确定U_stack、U_stack2 中的层数，具体规则见表1。

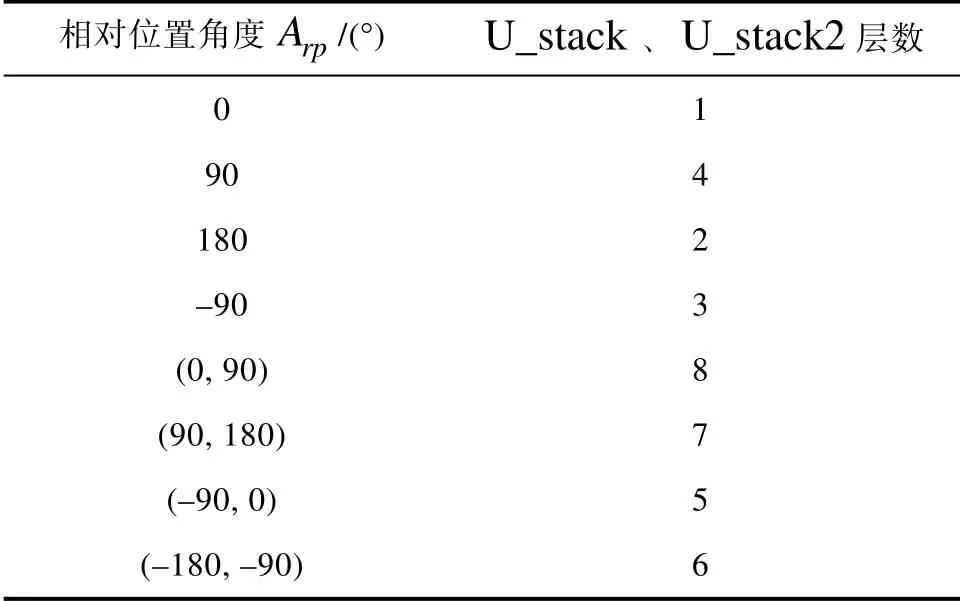
表1 能源消耗启发函数算法规则表Table 1 Rule table of energy consumption heuristic function algorithm

根据(xi,yi)、Dheu、Sheu和Arp选择对应的启发路径上速度堆U_stack、U_stack2 中的所有海洋能驱动航行器相对于大地的速度{vu2e}、海洋能驱动航行器相对于风的速度{vu2w}。接着利用式(11)依次计算从当前节点pcur(x,y)的周围8 个节点(xi,yi)到目标点(xgoal,ygoal)的启发能源消耗量，并取最小值作为下一步预估的能源消耗eheuristic2(x,y)。

将Estar_fun2 带入A*算法，得到考虑海流消耗和风能捕获的能源最优A*全局规划算法。

5 算法仿真试验与分析

通过在相同海况与相同风场环境下传统A*算法，C-A*，N-A*的能源消耗情况进行对比，开展仿真实验，对所提算法的可行性和有效性进行验证。

对于现实海况，海洋环境并非恒定，具有不规律不确定的特征。本文研究海洋环境的影响时采用简化模型，假设海流是均定流，海风为匀速风，从而讨论海流和海风对海洋能驱动航行器的能耗作用以及对全局路径规划的影响。

由于现有海洋能驱动航行器研究较少，经验公式还不完善，通过经验公式方法计算海浪干扰力，不仅方法繁琐复杂，同时计算的干扰力误差大，不满足实验要求，借助流体力学软件（CFD）估算也会有较大误差。并且根据文献[20]可以得知若波浪波长超出船长1.5 倍及以上后，波浪干扰力会很小。故本文暂不考虑波浪产生的阻力影响。

仿真环境1：静水状态风速为0

传统A*算法的结果路径如图4所示，C-A*、N-A*的结果路径如图5 和图6所示。

图4 传统A*算法结果Fig.4 Traditional A* algorithm results

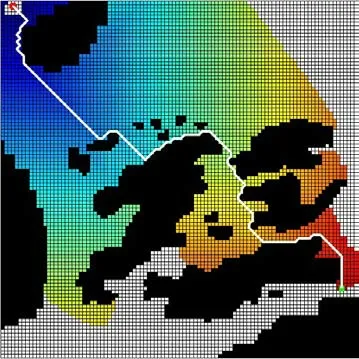
图5 C-A*算法结果Fig.5 C-A* algorithm results

图6 N-A*算法结果Fig.6 N-A* algorithm results

算法对比结果见表2，可以看出，在静水情况下 N-A*的能源消耗要少于传统 A*算法和C-A*算法。由于传统A*算法在静水中能够得到最短路径，所以传统A*算法消耗的能量也比较少。另外，对比C-A*与N-A*的结果可以发现，N-A*的能源消耗较少。综上所述，在静水环境下N-A*是能源最优的算法，传统A*算法次之，C-A*最差。

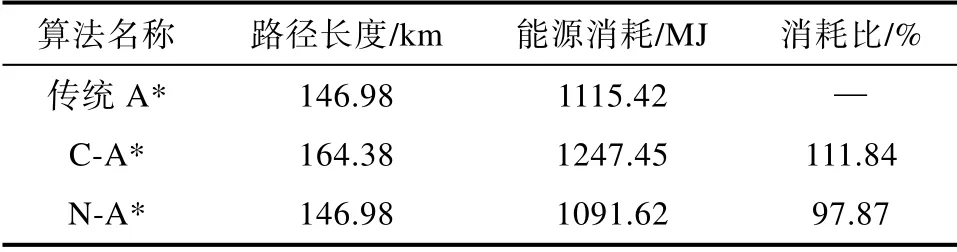
表2 静水中的算法对比结果Table 2 Algorithm comparison results in still water

仿真环境2：低流速0.6m/s，低风速6m/s

传统A*算法的结果路径同上，C-A*、N-A*的结果路径如图7、图8所示，算法对比结果见表3。

图7 海流流速0.6 m/s 中的C-A*算法结果Fig.7 C-A* algorithm result in sea current flow rate 0.6 m/s

从算法对比结果可以看出，在海流0.6 m/s的作用下，N-A*是能源最优的算法，C-A*次之，传统A*算法最差。C-A*相较传统A*算法所规划出的路径节约了25%的能源消耗；N-A*相较传统A*所规划出的路径节约了30%的能源消耗。

仿真环境3：高流速1.2 m/s，高风速14m/s

传统A*算法的结果路径同上，C-A*、N-A*的结果路径如图9、图10所示，算法对比结果见表4。

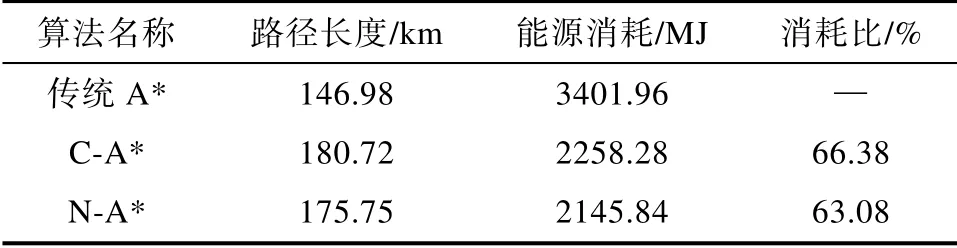
表4 海流流速1.2 m/s 中的算法对比结果Table 4 Comparison results of algorithms in ocean current velocity 1.2 m/s

图9 海流流速1.2 m/s 中的C-A*算法结果Fig.9 C-A* algorithm result in sea current flow rate 1.2 m/s

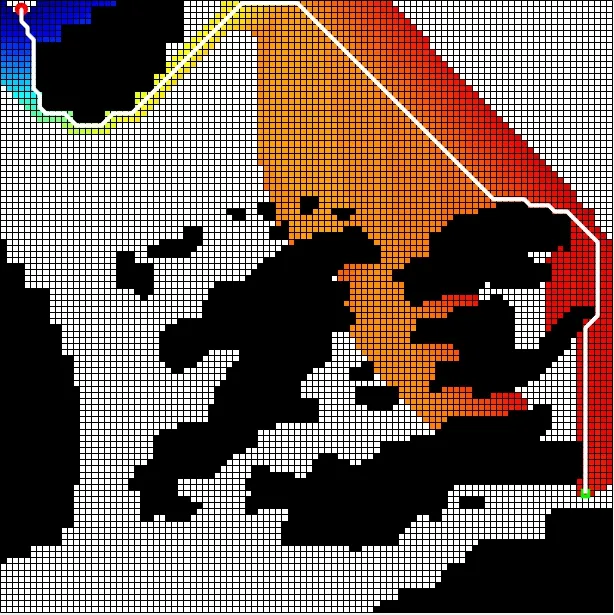
图10 海流流速1.2 m/s 中的N-A*算法结果Fig.10 N-A* algorithm result in sea current flow rate 1.2 m/s

从算法对比结果可以看出，在海流1.2m/s 的作用下，N-A*是能源最优的算法，C-A*次之，传统A*算法最差。C-A*相较传统A*算法所规划出的路径节约了33%的能源消耗；N-A*相较传统A*所规划出的路径节约了37%的能源消耗。

综合以上结果可知，在海流流速不为0 的情况下，C-A*、N-A*所规划出的路径都要比传统A*算法所规划出的路径要节约更多的能源，N-A*是能源最优的算法，C-A*次之。而且C-A*和N-A*的节能效果会随着海流的增大而增加。此外，就C-A*而言，虽然其能源消耗情况比N-A*差，但随着海流的增加，其能源消耗情况在不断地接近N-A*，所以在实际应用过程中，可以根据具体情况进行算法的选择。

6 结论

针对于海洋能驱动航行器的能源最优航迹规划问题，在传统距离寻优的A*算法基础上，考虑海洋能驱动航行器航行过程中的能源消耗问题和海洋能利用问题，建立考虑海流影响的能源消耗模型和风能捕获模型，对传统A*算法的消耗函数、启发函数和寻优函数进行改进，完成能源最优A*算法的研究，并对该算法进行仿真对比验证。主要结论如下。

（1）针对海洋能驱动航行器的全局路径规划问题，选取我国南海部分海域作为研究对象，采用栅格法，建立栅格地图环境模型。

（2）利用A*算法进行路径规划研究。建立考虑海流影响的能源消耗模型和风能捕获模型。根据上述模型，改进A*算法的消耗函数、启发函数和寻优函数，完成海洋能驱动航行器的能源最优航迹规划研究。

（3）在不同的环境状况下，对传统A*算法、C-A*、N-A*进行仿真试验，对比其能源消耗情况，分析表明，N-A*是能源最优的算法，C-A*次之，传统A*算法最差。随着流速的增加，C-A*和N-A*的节能效果在不断增加。